乘法数字谜.pptx
- 格式:pptx
- 大小:27.22 KB
- 文档页数:2
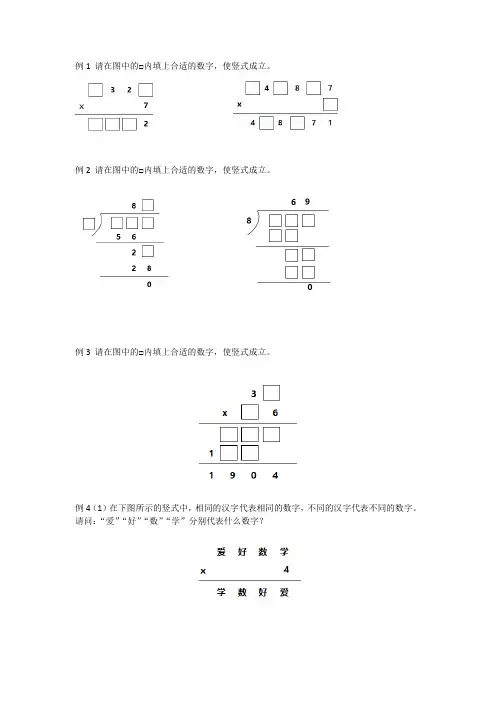
例1 请在图中的□内填上合适的数字,使竖式成立。
例2 请在图中的□内填上合适的数字,使竖式成立。
例3 请在图中的□内填上合适的数字,使竖式成立。
例4(1)在下图所示的竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请问:“爱”“好”“数”“学”分别代表什么数字?(2)在下图所示的竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请问:“车”“马”“炮”分别代表什么数字?自我挑战1、请在图中的□内填上合适的数字,使竖式成立。
2、请在图中的□内填上合适的数字,使竖式成立。
大显身手1、请在图中的□内填上合适的数字,使竖式成立。
2、请在图中的□内填上合适的数字,使竖式成立。
3、请在图中的□内填上合适的数字,使竖式成立。
4、在下图所示的竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请问:“哆”“啦”“A”“梦”分别代表什么数字?知识回顾1、等差数列2,5,8,11,14,…,问这个数列的第16项是多少?第32项呢?2、(1)等差数列6,7,8,9,10,…,其中25是这个数列的第几项?(2)等差数列3,6,9,12,15,…,69,这个数列共有多少项?3、等差数列计算(1)16+19+22+25+28+31+34+37(2)1+3+5+7+9+11+13+15+174、等差数列计算(1)2+5+8+…+29(2)3+7+11+15+…+79夯实基础1、请在图中的□内填上合适的数字,使竖式成立。
2、请在图中的□内填上合适的数字,使竖式成立。
3、请在图中的□内填上合适的数字,使竖式成立。
4、在下图所示的竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请问:“我爱广阔祖国”代表的六位数是多少?5、请在图中的□内填上合适的数字,使竖式成立。
自我挑战1、请在图中的□内填上合适的数字,使竖式成立。
2、在下图所示的竖式中,相同的符号代表相同的数字,不同的符号代表不同的数字,那么☆,△,○分别代表什么数字?3、下面的除法竖式中,商是____________。


第一讲乘除法数字谜(一)专题简析:解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
例1.在下面的方框中填上合适的数字。
分析:由积的末尾是0,可推出第二个因数的个位是5;由第二个因数的个位是5,并结合第一个因数与5相乘的积的情况考虑,可推出第一人个因数的百位是3;由第一个因数为376与积为31□□0,可推出第二个因数的十数上是8。
题中别的数字就容易填了。
练习一第二讲乘除法数字谜(二)例1.下面算式中的a、b、c、d这四个字母各代表什么数字?分析:因为四位数abcd乘9的积是四位数,可知a是1;d和9相乘的积的个位是1,可知d只能是9;因为第二个因数9与第一个因数百位上的数b相乘的积不能进位,所以b只能是0(1已经用过);再由b=0,可推知c=8。
练习二第三讲图形的个数例1.下面图形中有多少个正方形?分析:图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18+10+4=32个正方形。
例2.下图中共有多少个三角形?分析:为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6+3+4+1=14个三角形。
练习三1.下图中共有多少个正方形?2.下图中共有多少个正方形?3.下图中共有多少个正方形,多少个三角形?4.下面图中共有多少个三角形?第四讲找出数字的排列规律(一)找规律是我们在生活、学习、工作中经常使用的一种思想方法,在解数学题时人们也常常使用它,下面我们利用找规律的方法来解一些简单的数列问题。

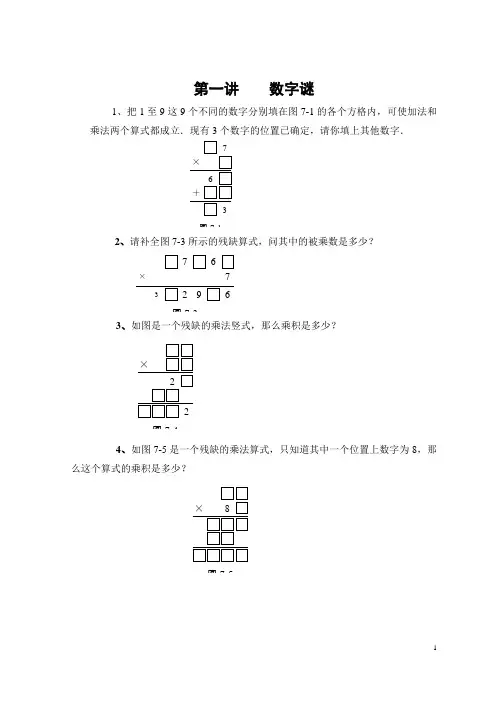
第一讲数字谜1、把1至9这9个不同的数字分别填在图7-1的各个方格内,可使加法和乘法两个算式都成立.现有3个数字的位置已确定,请你填上其他数字.图7-12、请补全图7-3所示的残缺算式,问其中的被乘数是多少?3、如图是一个残缺的乘法竖式,那么乘积是多少?4、如图7-5是一个残缺的乘法算式,只知道其中一个位置上数字为8,那么这个算式的乘积是多少?5、如图是一个残缺的乘法算式,补全后它的乘积是多少?6、如图所示的残缺算式中只知道3个位置上的数字是4,那么补全后它的乘积是多少?7、如图是一个残缺的乘法算式,补全后这个算式的乘积应是多少?8、如图是一个残缺的乘法算式,补全后这个算式的乘积应是多少?8、如图所示除法竖式的每个方框中,填入适当的数字,使算式成立.那么算式中的被除数是多少?9、如图所示的除法算式.10、如图所示的残缺除法算式,问其中的被除数应是多少?2 7378711、如图11是一个残缺的除法算式,将它补全后,被除数是多少?5274724769⨯=。
我们做标记如图。
可知A 与B 乘积个位数是5,与C 的乘积的个位数是9,显然B=5,而A 是3、7中的某一个。
1)若A=3,则C=3,经检验不能成立。
2)若A=7,则C=7,经检验D=4,E=2。
12、在如图所示的除法算式的每个空格内填入恰当的数字后,可使竖式成立,并且满足商与被除数个位数字相等的条件,将这个竖式写成横式是 .答案:1005÷3=335和1035÷9=115.显然竖式第四行中的两位数的首位为1,故第三行的一位数是9,从而除数为3或9.无0 0图49 0 图5论哪种情况,为保证商与被除数的个位相等,这个相同的数字只能为5.于是当除数为3时,所得的商是335,算式是335⨯3=1005;当除数为9时,所得的商是115,算式是115⨯9=1035.13、在图中所示的除法算式中填入合适的数字,使得等式成立,那么其中的商是________。
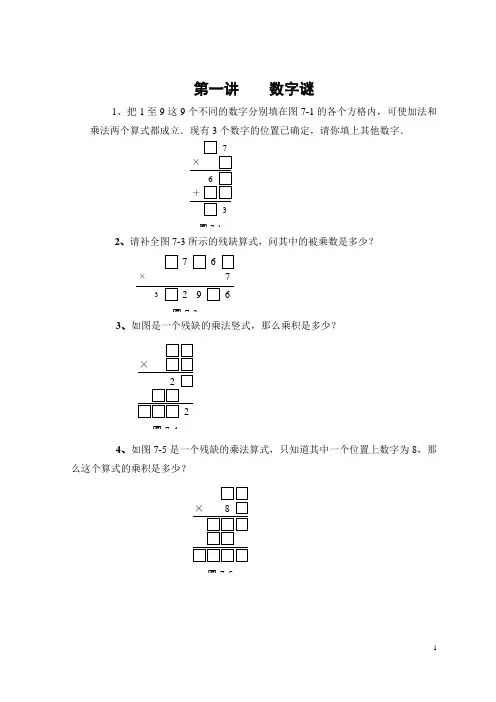
第一讲数字谜1、把1至9这9个不同的数字分别填在图7-1的各个方格内,可使加法和乘法两个算式都成立.现有3个数字的位置已确定,请你填上其他数字.图7-12、请补全图7-3所示的残缺算式,问其中的被乘数是多少?3、如图是一个残缺的乘法竖式,那么乘积是多少?4、如图7-5是一个残缺的乘法算式,只知道其中一个位置上数字为8,那么这个算式的乘积是多少?5、如图是一个残缺的乘法算式,补全后它的乘积是多少?6、如图所示的残缺算式中只知道3个位置上的数字是4,那么补全后它的乘积是多少?7、如图是一个残缺的乘法算式,补全后这个算式的乘积应是多少?8、如图是一个残缺的乘法算式,补全后这个算式的乘积应是多少?8、如图所示除法竖式的每个方框中,填入适当的数字,使算式成立.那么算式中的被除数是多少?9、如图所示的除法算式.10、如图所示的残缺除法算式,问其中的被除数应是多少?2 7378711、如图11是一个残缺的除法算式,将它补全后,被除数是多少?5274724769⨯=。
我们做标记如图。
可知A 与B 乘积个位数是5,与C 的乘积的个位数是9,显然B=5,而A 是3、7中的某一个。
1)若A=3,则C=3,经检验不能成立。
2)若A=7,则C=7,经检验D=4,E=2。
12、在如图所示的除法算式的每个空格内填入恰当的数字后,可使竖式成立,并且满足商与被除数个位数字相等的条件,将这个竖式写成横式是 .答案:1005÷3=335和1035÷9=115.显然竖式第四行中的两位数的首位为1,故第三行的一位数是9,从而除数为3或9.无0 0图49 0 图5论哪种情况,为保证商与被除数的个位相等,这个相同的数字只能为5.于是当除数为3时,所得的商是335,算式是335⨯3=1005;当除数为9时,所得的商是115,算式是115⨯9=1035.13、在图中所示的除法算式中填入合适的数字,使得等式成立,那么其中的商是________。

第一讲乘除法数字谜(一)专题简析:解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
例1.在下面的方框中填上合适的数字。
分析:由积的末尾是0,可推出第二个因数的个位是5;由第二个因数的个位是5,并结合第一个因数与5相乘的积的情况考虑,可推出第一人个因数的百位是3;由第一个因数为376与积为31□□0,可推出第二个因数的十数上是8。
题中别的数字就容易填了。
练习一第二讲乘除法数字谜(二)例1.下面算式中的a、b、c、d这四个字母各代表什么数字?分析:因为四位数abcd乘9的积是四位数,可知a是1;d和9相乘的积的个位是1,可知d只能是9;因为第二个因数9与第一个因数百位上的数b相乘的积不能进位,所以b只能是0(1已经用过);再由b=0,可推知c=8。
练习二第三讲图形的个数例1.下面图形中有多少个正方形?分析:图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18+10+4=32个正方形。
例2.下图中共有多少个三角形?分析:为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6+3+4+1=14个三角形。
练习三1.下图中共有多少个正方形?2.下图中共有多少个正方形?3.下图中共有多少个正方形,多少个三角形?4.下面图中共有多少个三角形?第四讲找出数字的排列规律(一)找规律是我们在生活、学习、工作中经常使用的一种思想方法,在解数学题时人们也常常使用它,下面我们利用找规律的方法来解一些简单的数列问题。

第一讲乘除法数字谜(一)专题简析:解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
例1.在下面的方框中填上合适的数字。
分析:由积的末尾是0,可推出第二个因数的个位是5;由第二个因数的个位是5,并结合第一个因数与5相乘的积的情况考虑,可推出第一人个因数的百位是3;由第一个因数为376与积为31□□0,可推出第二个因数的十数上是8。
题中别的数字就容易填了。
练习一第二讲乘除法数字谜(二)例1.下面算式中的a、b、c、d这四个字母各代表什么数字?分析:因为四位数abcd乘9的积是四位数,可知a是1;d和9相乘的积的个位是1,可知d只能是9;因为第二个因数9与第一个因数百位上的数b相乘的积不能进位,所以b只能是0(1已经用过);再由b=0,可推知c=8。
练习二第三讲图形的个数例1.下面图形中有多少个正方形?分析:图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18+10+4=32个正方形。
例2.下图中共有多少个三角形?分析:为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6+3+4+1=14个三角形。
练习三1.下图中共有多少个正方形?2.下图中共有多少个正方形?3.下图中共有多少个正方形,多少个三角形?4.下面图中共有多少个三角形?第四讲找出数字的排列规律(一)找规律是我们在生活、学习、工作中经常使用的一种思想方法,在解数学题时人们也常常使用它,下面我们利用找规律的方法来解一些简单的数列问题。


乘法竖式中的数字谜 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】第五讲乘法竖式中的数字谜姓名:题型概述:数字谜是一种有趣的猜数游戏。
要将乘法竖式中空缺的数字补上,解题时要看清竖式中己知的数字,根据运算法则,进行分析、推断、判断。
解数字谜时,一般可从某个数的首位或末位数字开始分析,填空要注意以下几个方面:(1)空格中只能填0~9,并且最高位上不能填0;(2)两个字相乘,最大的进位数是8;(3)在计算中进位数要留意,不能遗漏;(4)算式谜求出后,要进行验算。
例题一、在右面的算式中,不同的字母代表不同的数字,那么八位数“ABCDEFGH”表示多少?A B C D E F G H× 91 1 1 1 1 1 1 1 1分析:观察乘法算式中,可以发现己知两数的乘积111 111 111与乘数9,用除法可以算出八数是111 111 111÷9=12345679习题一、求算式的乘积。
× 5 2 × 71 3 6 6 9 3习题二、下面的算式中,相同的字母代表相同的数,不同的字母代表不同的数,字母有A、B、C、D、E分别代表几?1 A B C D E× 3A B C D E 1例题二、下面的乘法算式只知道其中的一个数字“8”,这个算式的乘积是多少?□□× 8 □□□□□□分析:乘数×8为一个两位数,被乘数可能是10、11、12.如果被乘数是10或11,那么与乘数个位数字相乘,积一定是两位数,与算式中的积是三位数互相矛盾,所以被乘数是12,乘数的个数只能为9,因此乘积为12×89=1068习题一、下面的算式中,A、B表示两个不同的数,当A、B分别表示几时,算式成立?A B× B A1 1 43 0 43 1 5 4习题二、求算式的乘积。
2 8 5×□□1 □2 □□□□□ 9 □□习题三、求算式的乘积。

第一讲乘除法数字谜(一)专题简析:解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
例1.在下面的方框中填上合适的数字。
分析:由积的末尾是0,可推出第二个因数的个位是5;由第二个因数的个位是5,并结合第一个因数与5相乘的积的情况考虑,可推出第一人个因数的百位是3;由第一个因数为376与积为31□□0,可推出第二个因数的十数上是8。
题中别的数字就容易填了。
练习一第二讲乘除法数字谜(二)例1.下面算式中的a、b、c、d这四个字母各代表什么数字?分析:因为四位数abcd乘9的积是四位数,可知a是1;d和9相乘的积的个位是1,可知d只能是9;因为第二个因数9与第一个因数百位上的数b相乘的积不能进位,所以b只能是0(1已经用过);再由b=0,可推知c=8。
练习二第三讲图形的个数例1.下面图形中有多少个正方形?分析:图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18+10+4=32个正方形。
例2.下图中共有多少个三角形?分析:为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6+3+4+1=14个三角形。
练习三1.下图中共有多少个正方形?2.下图中共有多少个正方形?3.下图中共有多少个正方形,多少个三角形?4.下面图中共有多少个三角形?第四讲找出数字的排列规律(一)找规律是我们在生活、学习、工作中经常使用的一种思想方法,在解数学题时人们也常常使用它,下面我们利用找规律的方法来解一些简单的数列问题。
第一讲乘除法数字谜(一)专题简析:解决算式谜题,关键是找准突破口,推理时应注意以下几点:1.认真分析算式中所包含的数量关系,找出隐蔽条件,选择有特征的部分作出局部判断;2.利用列举和筛选相结合的方法,逐步排除不合理的数字;3.试验时,应借助估值的方法,以缩小所求数字的取值范围,达到快速而准确的目的;4.算式谜解出后,要验算一遍。
例1.在下面的方框中填上合适的数字。
分析:由积的末尾是0,可推出第二个因数的个位是5;由第二个因数的个位是5,并结合第一个因数与5相乘的积的情况考虑,可推出第一人个因数的百位是3;由第一个因数为376与积为31□□0,可推出第二个因数的十数上是8。
题中别的数字就容易填了。
练习一第二讲乘除法数字谜(二)例1.下面算式中的a、b、c、d这四个字母各代表什么数字?分析:因为四位数abcd乘9的积是四位数,可知a是1;d和9相乘的积的个位是1,可知d只能是9;因为第二个因数9与第一个因数百位上的数b相乘的积不能进位,所以b只能是0(1已经用过);再由b=0,可推知c=8。
练习二第三讲图形的个数例1.下面图形中有多少个正方形?分析:图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18+10+4=32个正方形。
例2.下图中共有多少个三角形?分析:为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6+3+4+1=14个三角形。
练习三1.下图中共有多少个正方形?2.下图中共有多少个正方形?3.下图中共有多少个正方形,多少个三角形?4.下面图中共有多少个三角形?第四讲找出数字的排列规律(一)找规律是我们在生活、学习、工作中经常使用的一种思想方法,在解数学题时人们也常常使用它,下面我们利用找规律的方法来解一些简单的数列问题。