主成分分析方法

主成分分析法pca的流程
主成分分析（PCA）是一种常见的数据降维方法，其主要流程如下：
1. 数据预处理：先对原始数据进行标准化（均值中心化和方差缩放），保证各个维度数据具有可比性。

2. 计算协方差矩阵：通过样本数据求解协方差矩阵，反映各个变量间的线性相关性。

3. 特征值与特征向量计算：对协方差矩阵进行特征值分解或奇异值分解，得到对应的特征值和特征向量。

4. 选择主成分：按照特征值大小排序，选择前k个最大特征值对应的特征向量作为新的坐标轴（主成分）。

5. 数据转换：将原始数据投影到选定的主成分上，实现降维，新坐标系下的数据称为主成分得分。

6. 解释主成分：根据特征向量的结构理解主成分代表的含义，并可能通过累计贡献率评估降维效果。

总之，PCA通过挖掘数据内在结构，将高维数据转换为低维表示，同时保留主要变异信息。

主成分分析的步骤与实施方法主成分分析（Principal Component Analysis，简称PCA）是一种常用的降维数据分析方法，常用于数据预处理和特征提取。

本文将介绍主成分分析的基本步骤以及实施方法，帮助读者了解并应用于实际问题。

1. 数据预处理在进行主成分分析之前，首先需要进行数据预处理。

数据预处理包括数据清洗、归一化等操作，以确保数据的准确性和可靠性。

常见的数据预处理方法有：（1）数据清洗：排除异常值和缺失值，保证数据的完整性和一致性；（2）数据归一化：将数据转化为同一尺度，消除因为数据量纲不同而导致的误差；（3）数据标准化：将数据按照均值为0，方差为1进行线性变换，使得数据服从标准正态分布。

2. 计算协方差矩阵主成分分析的核心是通过计算协方差矩阵来确定数据之间的相关性。

协方差矩阵可以帮助我们找到数据的主要变化方向，进而找到主要成分。

协方差矩阵的计算步骤如下：（1）假设我们有m个n维数据，将其组成m×n的矩阵X；（2）计算X的协方差矩阵C，公式为：C = (X - μ)(X - μ)T / m，其中μ为X的均值向量；（3）计算协方差矩阵C的特征值和特征向量。

3. 计算主成分通过计算协方差矩阵的特征值和特征向量，我们可以得到数据的主成分。

主成分是协方差矩阵的特征向量按对应的特征值从大到小排列后所得到的矩阵。

计算主成分的步骤如下：（1）选择特征值较大的前k个特征向量，其中k为需要降维的维数；（2）将选择出的k个特征向量组成一个投影矩阵P；（3）对原始数据进行降维处理，将原始数据矩阵X与投影矩阵P相乘，得到降维后的数据矩阵Y。

4. 数据重构主成分分析完成后，我们可以通过数据重构来验证主成分的有效性。

重构后的数据尽量保持与原始数据的一致性，以确保降维后的数据仍能保持原有信息的完整性。

数据重构的步骤如下：（1）根据降维后的数据矩阵Y和投影矩阵P，计算重构矩阵X'，公式为：X' = YP' + μ，其中P'为投影矩阵的转置；（2）将重构矩阵X'与原始数据矩阵X进行对比，评估主成分提取的效果。

主成分分析方法
主成分分析方法是一种统计学技术，用于通过数据降低维数，它将多变量间的关系简化成少量的主成分，以把原来的多维变量映射到一维或者更少的维度空间。

主成分分析方法既可以用于对描述性数据的研究，也可以用于预测数据模型，它可以帮助估计定量指标与预测变量之间的关系，并降低多变量试验数据的维数。

主成分分析方法是一种数据处理技术，它主要用于减少维数，把原来的多变量压缩成少量的主成分。

它还可以用于描述多变量之间的关系，并降低有关模型之间的维数。

主成分分析方法的基本原理是，先把原来的n个变量分解成n个协方差矩阵，然后把它们求和，计算出协方差矩阵的特征值和特征向量，即主成分，接着，取出最大的特征值对应的特征向量，最后得到第一个主成分。

然后，用第一个主成分代替n个变量来表示n个变量，同时还可以利用空间的关系，把原来的n个变量转换成n-1个新变量，以此类推，一直到只有一个主成分为止。

主成分分析方法具有众多优势。

首先，它可以去除重复的信息，使用降维后的特征向量可以有效减少重复信息。

其次，它可以降低原始数据的数量，因为原始数据的降维，数据量就会减少。

此外，主成分分析方法可以有效去除噪声，因为它可以提取一组准确的特征。

最后，主成分分析方法还可以用于模型预测，它可以帮助估计定量指标与预测变量之间的关系，从而提高预测的准确性。

总之，主成分分析方法具有简单、快速、有效的特点，可以有效
地减少多变量之间的维度，及其在统计学和机器学习领域的广泛应用，极大地提升了研究成果的准确性和可信度。

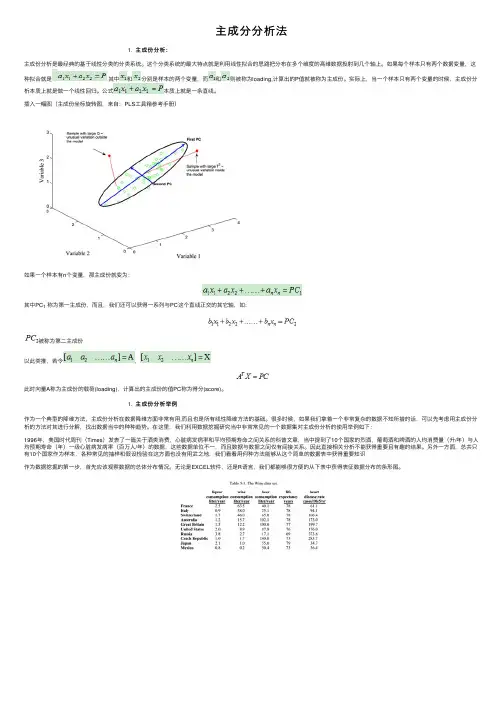
主成分分析法1. 主成份分析：主成份分析是最经典的基于线性分类的分类系统。

这个分类系统的最⼤特点就是利⽤线性拟合的思路把分布在多个维度的⾼维数据投射到⼏个轴上。

如果每个样本只有两个数据变量，这种拟合就是其中和分别是样本的两个变量，⽽和则被称为loading,计算出的P值就被称为主成份。

实际上，当⼀个样本只有两个变量的时候，主成份分析本质上就是做⼀个线性回归。

公式本质上就是⼀条直线。

插⼊⼀幅图（主成份坐标旋转图，来⾃：PLS⼯具箱参考⼿册）如果⼀个样本有n个变量，那主成份就变为：其中PC1 称为第⼀主成份，⽽且，我们还可以获得⼀系列与PC这个直线正交的其它轴，如：被称为第⼆主成份以此类推，若令，此时向量A称为主成份的载荷(loading)，计算出的主成份的值PC称为得分(score)。

1. 主成份分析举例作为⼀个典型的降维⽅法，主成份分析在数据降维⽅⾯⾮常有⽤,⽽且也是所有线性降维⽅法的基础。

很多时候，如果我们拿着⼀个⾮常复杂的数据不知所措的话，可以先考虑⽤主成份分析的⽅法对其进⾏分解，找出数据当中的种种趋势。

在这⾥，我们利⽤数据挖掘研究当中⾮常常见的⼀个数据集对主成份分析的使⽤举例如下：1996年，美国时代周刊（Times）发表了⼀篇关于酒类消费，⼼脏病发病率和平均预期寿命之间关系的科普⽂章，当中提到了10个国家的烈酒，葡萄酒和啤酒的⼈均消费量（升/年）与⼈均预期寿命（年）⼀级⼼脏病发病率（百万⼈/年）的数据，这些数据单位不⼀，⽽且数据与数据之间仅有间接关系。

因此直接相关分析不能获得重要且有趣的结果。

另外⼀⽅⾯，总共只有10个国家作为样本，各种常见的抽样和假设检验在这⽅⾯也没有⽤武之地，我们看看⽤何种⽅法能够从这个简单的数据表中获得重要知识作为数据挖掘的第⼀步，⾸先应该观察数据的总体分布情况。

⽆论是EXCEL软件，还是R语⾔，我们都能够很⽅便的从下表中获得表征数据分布的条形图。

从图中可以看出，总共10个国家，有5类数据，由于各类数据性质各不相同，因此数值上⼤⼩也很不相同。

主成分分析法主成分分析法是一种数学变换的方法, 它把给定的一组相关变量通过线性变换转成另一组不相关的变量，这些新的变量按照方差依次递减的顺序排列。

在数学变换中保持变量的总方差不变，使第一变量具有最大的方差，称为第一主成分，第二变量的方差次大，并且和第一变量不相关，称为第二主成分。

依次类推，I个变量就有I个主成分。

其中Li为p维正交化向量（Li＊Li＝1），Zi之间互不相关且按照方差由大到小排列，则称Zi为X的第I个主成分。

10本词条无基本信息模块, 欢迎各位编辑词条，额外获取10个积分。

目录1基本定义2分析目的3分析步骤4因子旋转5应用问题个主成分Zi所对应的系数向量Li，而Zi的方差贡献率定义为λi／Σλj,通常要求提取的主成分的k满足Σλk／Σλj>0.85。

2分析目的是希望用较少的变量去解释原来资料中的大部分变量，将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。

通常是选出比原始变量个数少，能解释大部分资料中变量的几个新变量，即所谓主成分，并用以解释资料的综合性指标。

由此可见，主成分分析实际上是一种降维方法。

3分析步骤数据标准化;求相关系数矩阵;一系列正交变换，使非对角线上的数置0，加到主对角上;得特征根xi（即相应那个主成分引起变异的方差),并按照从大到小的顺序把特征根排列;求各个特征根对应的特征向量;用下式计算每个特征根的贡献率Vi;Vi=xi/(x1+x2+........)根据特征根及其特征向量解释主成分物理意义。

4因子旋转在对社会调查数据进行分析时，除了把相关的问题综合成因子并保留大的因子，研究者往往还需要对因子与测度项之间的关系进行检验，以确保每一个主要的因子（主成分）对应于一组意义相关的测度项。

为了更清楚的展现因子与测度项之间的关系，研究者需要进行因子旋转。

常见的旋转方法是VARIMAX旋转。

旋转之后，如果一个测度项与对应的因子的相关度很高（>0.5)就被认为是可以接受的。

主成分分析方法在经济问题的研究中，我们常常会遇到影响此问题的很多变量，这些变量多且又有一定的相关性，因此我们希望从中综合出一些主要的指标，这些指标所包含的信息量又很多。

这些特点，使我们在研究复杂的问题时，容易抓住主要矛盾。

那么怎样找综合指标？主成分分析是将原来众多具有一定相关性的指标重新组合成一组新的相互无关的综合指标来代替原来指标的统计方法,也是数学上处理降维的一种方法. 一. 主成分分析法简介主成分分析是将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法，又称主分量分析。

在实际问题中，为了全面分析问题，往往提出很多与此有关的变量（或因素），因为每个变量都在不同程度上反映这个课题的某些信息。

但是，在用统计分析方法研究这个多变量的课题时，变量个数太多就会增加课题的复杂性。

人们自然希望变量个数较少而得到的信息较多。

在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。

主成分分析是对于原先提出的所有变量，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映问题的信息方面尽可能保持原有的信息。

信息的大小通常用离差平方和或方差来衡量。

主成分分析的基础思想是将数据原来的p 个指标作线性组合,作为新的综合指标(P F F F ,,,21 )。

其中1F 是“信息最多”的指标，即原指标所有线性组合中使)var(1F 最大的组合对应的指标，称为第一主成分；2F 为除1F 外信息最多的指标，即0),cov(21 F F 且)var(2F 最大，称为第二主成分；依次类推。

易知P F F F ,,,21 互不相关且方差递减。

实际处理中一般只选取前几个最大的主成分（总贡献率达到85%），达到了降维的目的。

主成分的几何意义：设有n 个样品，每个样品有两个观测变量,,21X X 二维平面的散点图。

n 个样本点，无论沿着1X 轴方向还是2X 轴方向，都有较大的离散性，其离散程度可以用1X 或2X 的方差表示。

主成分分析方法简介在经济问题的研究中，我们常常会遇到影响此问题的很多变量，这些变量多且又有一定的相关性，因此我们希望从中综合出一些主要的指标，这些指标所包含的信息量又很多。

这些特点，使我们在研究复杂的问题时，容易抓住主要矛盾。

那么怎样找综合指标？主成分分析是将原来众多具有一定相关性的指标重新组合成一组新的相互无关的综合指标来代替原来指标的统计方法,也是数学上降维的一种方法.一. 主成分分析法简介主成分分析是将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法，又称主分量分析。

在实际问题中，为了全面分析问题，往往提出很多与此有关的变量（或因素），因为每个变量都在不同程度上反映这个问题的某些信息。

但是，在用统计分析方法研究这个多变量的问题时，变量个数太多就会增加问题的复杂性。

人们自然希望变量个数较少而得到的信息较多。

在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此问题的信息有一定的重叠。

主成分分析是对于原先提出的所有变量，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映问题的信息方面尽可能保持原有的信息。

信息的大小通常用离差平方和或方差来衡量。

主成分分析的基础思想是将数据原来的p 个指标作线性组合,作为新的综合指标(P F F F ,,,21 )。

其中1F 是“信息最多”的指标，即原指标所有线性组合中使)var(1F 最大的组合对应的指标，称为第一主成分；2F 为除1F 外信息最多的指标，即0),cov(21 F F 且)var(2F 最大，称为第二主成分；依次类推。

易知P F F F ,,,21 互不相关且方差递减。

实际处理中一般只选取前几个最大的主成分（总贡献率达到85%），达到了降维的目的。

主成分分析是一种进行信息压缩的方法。

通过这种方法，可以将原来相关的若干变量，变换成不相关的变量。

二.求主成分方法步骤：（1）对样本数据的标准化设有n个样品，P个指标，得到的原始资料矩阵为了实现样本数据的标准化，应求样本数据的均值和方差。

主成分分析方法主成分分析方法是常用的一种统计分析方法,主要用于进行数据压缩或减少数据的维数[2]。

它是对一组相关的变量进行线性变换,得到一组维数不变但彼此互不相关的变量,亦即一组主成分。

由于各主成分是不相关的,因此可以认为它们是一组独立变量。

一般图像的线性变换可用下式表示:Y=TX (1)式中:X为待变换图像数据矩阵,Y为变换后的数据矩阵;T为实现这一线性变换的变换矩阵。

如果变换矩阵T是正交矩阵,并且它是由原始图像数据矩阵X的协方差矩阵S的特征向量所组成,则(1)式的线性变换称为主成分分析,并且变换后的数据矩阵的每一行矢量为主成分分析的一个主成分。

主成分分析的优点是消除了波段间的相互关系,减少了各波段提供信息的交叉和冗余,有利于分析。

同时,在分析过程中得到主要波段的合理权重,具有很好的客观性。

主成分分析法的主要步骤如下:(1)根据原始图像数据矩阵X,求出它的协方差矩阵S 以矩阵的形式表示多波段图像的原始数据如下:X=x11x12,x1nx21x22,x2ns s s sxn1xn1,xnn=[xij]m@n(2)矩阵X中,m,n分别为波段数和每幅图像中的像元数,矩阵中的每一行矢量表示一个波段的图像。

矩阵X的协方差矩阵S为:S=1n[X-Xl][X-Xl]T(3)式中:l=[1 1 , 1]1@n(4)X=[x1 x2 , x3]T(5)xi=1nEnk=1xik(第i波段的均值) (6)(2)求协方差矩阵S的特征值Ki和特征向量Ui,并组成变换矩阵T 求解特征方程(KI-S)U=0; 然后将特征值Ki按由小到大的顺序排列,求出对应特征值的单位特征向量Ui,以Ui为列构成矩阵U,U矩阵的转置矩阵,即UT为所求的变换矩阵T。

经过主成分变换后得到的新变量的各个行向量依次被称为第一主成分、第二主成分,,第m主成分,这时将新变量恢复为二维图像,便得到m个主成分图像。

4，主成分分析法主成分分析（Principal Component Analysis，PCA），是一种统计方法。

通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

主成分分析首先是由K.皮尔森（Karl Pearson）对非随机变量引入的，尔后H.霍特林将此方法推广到随机向量的情形。

信息的大小通常用离差平方和或方差来衡量。

②主成分的解释其含义一般多少带有点模糊性，不像原始变量的含义那么清楚、确切，这是变量降维过程中不得不付出的代价。

因此，提取的主成分个数m通常应明显小于原始变量个数p（除非p本身较小），否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。

③当主成分的因子负荷的符号有正有负时，综合评价函数意义就不明确。

4.4主成分分析法的运用叶晓枫，王志良,【2】在介绍主成分分析方法的基本思想及计算方法基础上,对水资源调配评价指标进行了降维计算. 结果显示筛选出的指标对原指标具有较好的代表性,简化了水资源评价问题的难度。

傅湘，纪昌明【3】，针对模糊综合评判法在综合评价中存在的主观随意性问题，提出采用主成分分析法进行区域水资源承载能力综合评价。

对各区域的灌溉率、水资源利用率、水资源开发程度、供水模数、需水模数、人均供水量和生态环境用水率达七个主要因索进行了分析；根据主成分分析法的原理，运用少数几个新的综合指标对原来的七个指标所包含的信息进行最佳综合与简化，研究其在各区域水资源开发利用过程中的不同贡献及综合效应。

周莨棋，徐向阳等【4】，针对传统主成分分析法用于水资源综合评价中存在一些问题，包括指标评价中的“线性”问题、无法体现评价指标主观重要性以及评价范围无法确定。

进行了改进，采用改进的极差正规方法对数据进行规格化，用规格化后的数据加入了主观重要性权进行协方差计算，对协方差特征向量采用正负理想点进行检验。

陈腊娇，冯利华等【5】，将主成分分析方法引入到水资源承载力研究中，并以浙江省为例，在现有资料的基础上，利用主成分分析的方法，定量分析影响水资源承载力变化的最主要的驱动因子。

主成分分析方法及其应用在数据分析和模式识别领域，主成分分析（Principal Component Analysis，简称PCA）是一种常用的降维技术和数据预处理方法。

该方法通过线性变换将高维数据映射为低维空间，同时保留尽可能多的数据信息。

本文将介绍主成分分析的基本原理和应用，并分析其在实际问题中的实用价值。

一、主成分分析的基本原理主成分分析的目标是通过线性变换将原始数据投影到一个新的坐标系上，使得新坐标系的第一主成分方差最大，第二主成分方差次之，依此类推。

这样做的好处是降低数据的维度，去除冗余信息，同时保留数据的主要特征。

下面是主成分分析的基本步骤：1. 数据标准化在进行主成分分析之前，首先需要对数据进行标准化处理，确保各个特征具有相同的尺度。

通常使用零均值标准化方法，即对每个特征进行减去均值，再除以标准差。

2. 计算协方差矩阵协方差矩阵是描述各个特征之间相关性的一种方式。

通过计算标准化后数据的协方差矩阵，可以获取各个特征之间的相关性信息。

3. 特征值分解对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

特征向量表示了新坐标系的方向，特征值表示了数据在该方向上的方差大小。

4. 选择主成分根据特征值的大小选择主成分。

通常选择特征值较大的前几个主成分，它们包含了数据中大部分的信息。

5. 数据投影使用选取的主成分将数据投影到新的低维空间中。

投影后，数据的维度被降低，但保留了主要的结构信息。

二、主成分分析的应用主成分分析在实际问题中有广泛的应用。

以下列举了几个常见的应用领域：1. 特征提取主成分分析可以用于提取数据的主要特征，去除冗余信息。

在图像处理、语音识别等领域，主成分分析可以用于特征提取，从而减少特征的维度，简化后续分类或识别任务。

2. 数据压缩由于主成分分析可以降低数据的维度，因此可以用于数据的压缩。

通过保留较多的主成分，可以在一定程度上减小数据的存储空间和计算负担，提高数据处理的效率。

主成分分析法主成分分析旨在利用降维的思想，把多指标转化为少数几个综合指标。

在这个问题中为了全面、系统地分析问题，必须考虑众多影响因素。

因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而所得的统计数据反映的信息在一定程度上有重叠。

主成分分析法的方法：1、原始指标数据的标准化采集p 维随机向量x = (x1,X2,...,X p)T)n 个样品x i =(x i1,x i2,...,x ip)T，i=1,2,…,n，n＞p，构造样本阵，对样本阵元进行如下标准化变换：其中，得标准化阵Z。

2、对标准化阵Z 求相关系数矩阵其中,。

3、解样本相关矩阵R 的特征方程得p 个特征根,确定主成分按确定m 值，使信息的利用率达85%以上，对每个λj,j=1,2,...,m, 解方程组Rb = λj b得单位特征向量。

4、将标准化后的指标变量转换为主成分U1称为第一主成分,U2称为第二主成分,…,U p称为第p 主成分。

5 、对m 个主成分进行综合评价对m 个主成分进行加权求和，即得最终评价值，权数为每个主成分的方差贡献率。

题目中给出了八种元素，我们想将八种元素归类，分为至少两个类别，一边之后进行分析。

因此根据主成分分析法，对八种元素分类。

应用软件，先将数据标准化，之后可以得出：相关系数矩阵，方差分解主成分提取分析表以及起始因子载荷矩阵和评分，如下图所示：结论：根据以上结果，可以把八种重金属元素分为：Cd,Cu,Hg,Pb,Zn和Cr,As,Ni两类，与前面一种方法结果相似。

事实上分析问题的方法与模型很多，得出的结果也会有差异，因此可以结合两种不同的方法，根据具体问题，将结论融合得出结论。

为此，我们通过分析决定以第一种方法的分类标准来分析之后的问题。

因为在查阅资料后，发现这样分出的两个类别与实际比较相符，而且污染的原因也大致相似，所计算出的数据也与之较为相符。

主成分分析的方法
主成分分析（Principal Component Analysis，PCA）是一种常用的降维方法，通过线性变换将原始数据投影到一个新的空间中，使得数据在新的空间中的最大方差出现在第一个主成分上，第二大方差出现在第二个主成分上，以此类推。

这样可以保留较多的原始数据信息，同时减少数据的维度。

主成分分析的方法可以简洁地总结为以下几个步骤：
1. 标准化数据：将原始数据进行标准化处理，使得各个特征具有相同的尺度。

2. 计算协方差矩阵：计算标准化后的数据各个特征之间的协方差矩阵。

3. 计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

4. 选择主成分数量：根据特征值的大小选择主成分的数量，通常选择特征值大于某个阈值的主成分。

5. 构造变换矩阵：将特征值较大的特征向量作为基向量构造出变换矩阵，以实现数据的降维。

6. 数据投影：将原始数据通过变换矩阵进行投影，得到降维后的数据。

主成分分析的目标是选择能够最大程度保留原始数据信息的主成分，这可以通过保留最大方差或者最小重构误差来衡量。

主成分分析在数据预处理、特征提取和可视化等领域有广泛的应用。