下载文档原格式
昆明理工大学数值分析考试题（07）一．填空（每空3分，共30分）1． 设A 0.231x =是真值0.229T x =的近似值，则Ax 有 位有效数字。
2． 若74()631f x x x x =+++，则017[2,2,...2]f = ，018[2,2,...2]f = 。
3． A=1031⎡⎤⎢⎥-⎣⎦,则1A = ；A ∞= ；2A =2()cond A = 。
4． 求方程()x f x =根的牛顿迭代格式是 。
5．设105%x =±，则求函数()f x =的相对误差限为 。
6．A=2101202a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭,为使其可分解为TL L （L 为下三角阵，主对角线元素>0），a 的取值范围应为 。
7．用最小二乘法拟合三点A(0,1),B(1,3),C(2,2)的直线是 。
（注意：以上填空题答案标明题号答在答题纸上，答在试卷上的不给予评分。
）二．推导与计算（一）对下表构造f(x)的不超过3次的插值多项式，并建立插值误差公式。
（12分）（二）已知()x x =Φ和()x 'Φ满足∣()x 'Φ-3∣<1。
请利用()x Φ构造一个收敛的简单迭代函数()x ψ，使1(),0,1,......k k x x k +=ψ=收敛。
（8分）（三）利用复化梯形公式计算21x I e dx -=⎰，使其误差限为60.510-⨯，应将区间[0，1]等份。
（8分）（四）设A= 1001005a b b a ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，detA ≠0，推导用a ，b 表示解方程组AX=f 的Seidel(G-S) 迭代法收敛的充分必要条件。
（10分）（五）确定节点及系数，建立如下 GAUSS 型求积公式111220()()dx A f x A f x ≈+⎰。
（10分）（六）对微分方程初值问题'00(,)()y f x y y x y ⎧=⎨=⎩（１） 用数值积分法推导如下数值算法：1111(4)3n n n n n hy y f f f +-+-=+++，其中(,)i i i f f x y =，(1,,1)i n n n =-+。
昆明理工大学2018年博士研究生招生考试试题
考试科目代码：2021 考试科目名称：概率论与数理统计
考生答题须知
1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。
请考生务必在答题纸上写清题号。
2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。
3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。
4．答题时不准使用涂改液等具有明显标记的涂改用品。
第 1 页共4 页。
昆明理工大学2018年博士研究生招生考试试题
考试科目代码：2020 考试科目名称：运筹学
考生答题须知
1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。
请考生务必在答题纸上写清题号。
2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。
3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。
4．答题时不准使用涂改液等具有明显标记的涂改用品。
第 1 页共2 页。
昆明理工大学英语2018年考博真题博士入学试卷昆明理工大学2018年博士研究生招生考试试题（A）考试科目代码：1111 考试科目名称：英语试题适用招生专业：全校考生答题须知1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。
请考生务必在答题纸上写清题号。
2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。
3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。
4．答题时不准使用涂改液等具有明显标记的涂改用品。
Part I Structure and Vocabulary( 15 points )Directions: In this part, there are fifteen incomplete sentences. For each sentence four alternatives A, B, C or D are given. Decide which of the alternatives best completes the sentence and mark the corresponding letter on your ANSWER SHEET.1.When ______ at the door, she was given a warm welcome.A.appearB. appearedC. appearingD. appears2.Mr. Lee is far too wise a man not ______ that.A.seeingB. being seenC. seeD. to see3.The residents, ______ had been damaged by the flood, were given help by the Red Cross.A.all their homesB. all whose homesC.all of whose homesD. all of their homes4.______, I must do another experiment.A.Be it ever so lateB. It is ever so lateC.It be ever so lateD. So late it be ever5.I wish ______ to Stockholm when I was in Sweden. I hear it’sa beautiful city.A.I wentB. I had goneC. to goD. to have gone6.Tom ______ better than to ask Dick for help.A.shall knowB. has knownC. shouldn’t knowD. should have known7.There has been much opposition from some social groups, ______from the farmingcommunity.A.straightforwardlyB. notablyC. virtuallyD. exceptionally8.The ______ view in Britain and other Western countriesassociates aging with decline,dependency, isolation, and often poverty.A.predominantB. credulousC. inclusiveD. sustainable9.The foreman read the ______ of guilty fourteen times, one for each defendant.A.prejudiceB. verificationC. verdictD. punishment10.They fear it could have a(n) ______ effect on global financial markets.A.sizeableB. adverseC. beneficialD. consequential11.Just as you do not wish others to ______ their desires upon you, you must leave it to them tobe free to follow their own direction in life.A.inflictB. disputeC. ridiculeD. antedate12.The children have a more ______ view, only taking in consideration what will work.昆明理工大学2018年博士研究生招生考试试题第 1 页共 8 页。
昆明理工大学2018年博士研究生招生考试试题
考试科目代码：2013 考试科目名称：信号处理
考生答题须知
1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。
请考生务必在答题纸上写清题号。
2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。
3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。
4．答题时不准使用涂改液等具有明显标记的涂改用品。
一、用必要的公式、曲线、图表等形式，简要回答如下问题（每题10分，共40分）
1. 简述f(t)展开为傅里叶级数的狄里赫利条件。
2. 信号的基本运算有哪些？
3. 数字滤波器分为哪两大类？用差分方程描述时有什么不同？
它们各有什么特性？
4. 模拟巴特沃兹滤波器的极点在S平面上的分布有什么特点？
二、试用必要的公式、图例论述如下问题（每题20分，共60分）
1.
阐述离散傅里叶变换的基本原理和算法流程，解释频谱混叠和频谱泄漏产生的原因。
2.
阐述小波变换的基本原理和核心思想，描述一种小波算法，说明Heisenberg测不准原理在小波变换中的具体表现形式。
3. 阐述数学形态学的基本原理，并列举主要应用。
第 1 页共 3 页。
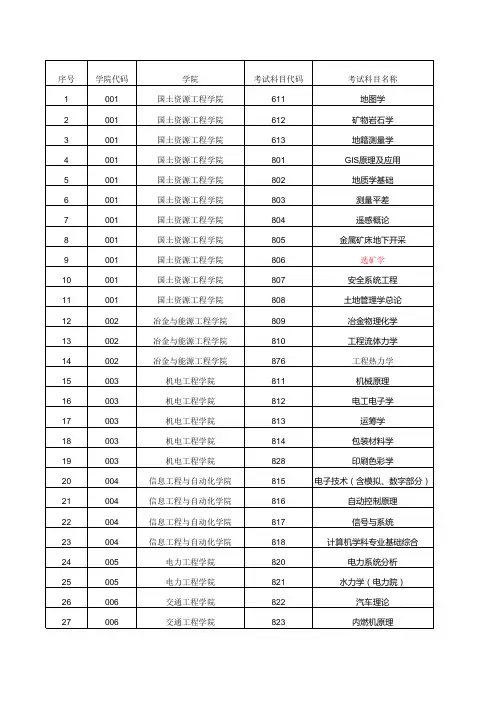
第 1 页 共 2 页昆明理工大学2018级硕士研究生试卷(A 卷)科目： 数值分析 考试时间： 出题教师： 集体 考生姓名： 专业： 学号：不予计分；可带计算器。
一、 填空题（每空2分，共40分）1．设*3.141x =是圆周率=3.1415926π的近似值，则*x 有 位有效数字，*x 的相对误差限为 。
（取四位非零小数） 2．设64()53f x x x =+，则f =]2,,2,2[610 。
3. 过点)0,2(),0,0(和)3,1(的二次拉格朗日插值函数为)(2x L = ， 并计算余项=)3(2R 。
4．设32()f x x x =+在[]1,1-上的最佳二次一致逼近多项式为 ，3()f x x =在[]1,1-上关于权()1x ρ=的最佳二次平方逼近多项式为 。
5．高斯求积公式10011-1()()()f x dx A f x A f x ≈+⎰的系数0A = ，1A = ，节点0x = ，1x =。
6．方程组b Ax=，11122122aa A a a⎛⎫= ⎪⎝⎭，建立迭代公式f Bx xk k +=+)()1(，写出雅可比迭代和高斯-赛德尔迭代的迭代矩阵，=J B ，=-S G B 。
7．正交矩阵A ⎫⎪⎪=，其2-范数下的条件数2()Cond A = 。
8．设⎥⎦⎤⎢⎣⎡=0.310.0.50.6A，计算矩阵A 的范数，1||||A = ， 2||||A = 。
第 2 页 共 2 页9． 求方程1sin x x +=的根的牛顿迭代格式是 ， 收敛阶是 。
10．对矩阵⎪⎪⎪⎭⎫⎝⎛=461561552621A 作LU 分解，其L=_______ ________，U=______ ___________。
二、计算题（每题10分，共50分）1. 求一个次数不高于3次的多项式P (x ), 使它满足: ，1)1(,1)0(,0)0('===p p p2)1('=p , 并写出其余项表达式。
第 1 页 共 4 页
昆明理工大学2018年博士研究生招生考试试题
考试科目代码： 2010 考试科目名称 ：现代控制工程
考生答题须知
1． 所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。
请考生务必在答题纸上写清题号。
2． 评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。
3． 答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。
4． 答题时不准使用涂改液等具有明显标记的涂改用品。
图1
分) 已知系统的矩阵A 的特征值λ（12i ,,,n =）是相异的，且A 矩阵为能控标准形，
1
2
100001n
n n a a a a --⎥⎥⎥⎥⎥---⎦
u =
图2 安装在手推车上的弹簧-质量-阻尼器系统。
2018年云南昆明理工大学数学分析考研真题A 卷一、计算及判断（每小题5分，共20分）1、设函数arctan ()x y f e=，求微分dy ； 2、求极限1321lim 242n n n→∞-⋅⋅⋅； 3、设函数1,77(),711(1)sin ,11x x f x x x x x x ⎧-∞<<-⎪+⎪=-≤≤⎨⎪⎪-<<+∞-⎩，指出其间断点及类型，并说明理由； 4、求函数()arctan f x x =在0x =的左、右导数．二、证明下列各题（每小题5分，共20分）1、用X ε-定义证明lim sin 0x x π→+∞=；2、叙述函数极限0lim ()x f x +→存在的归结原则； 3、运用归结原则证明01lim cos x x+→不存在；4、应用拉格朗日中值定理不等式：a a b a b b a b -<<-ln ，其中b a <<0． 三、（10分）证明：若函数f 在R 连续，且()()xa f x f t dt =⎰，则()0f x ≡． 四、（10分）证明：若数列{}n na 收敛，且级数11()n n n n aa ∞-=-∑收敛，则级数1n n a ∞=∑收敛． 五、计算或证明下列各题（每小题5分，共35分）1、求极限 221lim nn i n n i→∞=+∑； 2、求导数 32x x d dx ⎰； 3、证明瑕积分130arctan1x dx x-⎰发散; 4、求极限 00lim πα→⎰； 5、求函数()2x f x π-=在(0,2)π上的傅里叶展开式； 6、计算第一型曲线积分L yds ⎰，其中L 为单位上半圆周221x y +=； 7、计算第一型曲面积分SzdS ⎰⎰，其中S 为平面1=++z y x 在第一卦限中的部分.六、（10分）证明函数1,()1x f x x ⎧=⎨-⎩为有理数，，为无理数在]1,0[上有界但不可积． 七、（10分）求函数⎪⎩⎪⎨⎧=+≠++-=0,00 ,),(22222233y x y x y x y x y x f 在原点的偏导数)0,0(x f 与)0,0(y f , 并证明),(y x f 在点)0,0(是不可微的．八、（10分）利用适当的坐标变换计算二重积分{}()sin(),(,)0,0Dx y x y dxdy D x y x y x y ππ+-=≤+≤≤-≤⎰⎰．九、（10分）设f 是一元函数,试问应对f 提出什么条件,方程)()()(2y f x f xy f +=在点)1,1(的邻域内就能确定出唯一的y 为x 的函数?十、（10分）用高斯公式计算第二型曲面积分22()S yzdydz x z ydzdx xydxdy +++⎰⎰，其中22:4()S y x z =-+，在0x z 面右侧部分内侧.十一、（5分）请举例说明：在有理数集内，单调有界定理一般都不成立.。
