空间数据坐标系转换方法

三参数、四参数、七参数等坐标系转换参数求解-回复在地理信息系统（GIS）和空间数据处理中，经常需要进行不同坐标系之间的转换。

常见的坐标系转换方法包括三参数、四参数和七参数等。

本文将一步一步地讲解这些坐标系转换参数的求解方法。

1. 三参数坐标系转换参数求解三参数坐标系转换是一种基本的坐标系转换方法，适用于同一地区内的小范围转换。

这种方法使用三个参数来描述转换，分别是平移参数（delta X 和delta Y）和旋转参数（delta Z）。

其数学模型可以表示为：X_new = X_old + delta X + delta Z * Y_oldY_new = Y_old + delta Y - delta Z * X_oldZ_new = Z_old要求解这三个参数，通常需要至少三对已知的坐标点。

已知的坐标点可以是在两个不同坐标系中测量得到的。

下面是求解三参数坐标系转换参数的步骤：步骤1：选择至少三对已知的坐标点，并在两个不同坐标系中用坐标系A 和坐标系B表示。

步骤2：通过观察坐标系A和坐标系B之间的关系，将数学模型中的公式改写为总体误差最小的形式。

步骤3：将已知坐标点的坐标值代入改写后的数学模型，得到带有未知参数的方程组。

步骤4：通过数学方法求解方程组，得到三个参数的近似解。

步骤5：对参数的近似解进行迭代计算，直到满足预设的误差限度。

2. 四参数坐标系转换参数求解四参数坐标系转换是在三参数的基础上增加了一个尺度参数（scale factor）。

尺度参数描述了坐标系统之间的比例差异，通常用ppm（百万分之一）表示。

其数学模型可以表示为：X_new = X_old + delta X + ppm * Y_oldY_new = Y_old + delta Y - ppm * X_oldZ_new = Z_old与三参数的求解类似，四参数的求解也需要至少三对已知的坐标点。

下面是求解四参数坐标系转换参数的步骤：步骤1：选择至少三对已知的坐标点，并在两个不同坐标系中用坐标系A 和坐标系B表示。

gdal tiff转换坐标系gdal是一个用于处理地理空间数据的开源库，可以用于读取、写入和转换各种地理空间数据格式。

其中，将TIFF格式的地理空间数据转换为不同的坐标系是gdal的常见应用之一。

在使用gdal进行TIFF转换坐标系时，我们首先需要了解原始TIFF 文件的坐标系信息。

gdal可以通过读取TIFF文件的元数据来获取坐标系信息，包括投影信息（如投影类型、投影参数等）和地理坐标范围（如经纬度范围）。

这些信息对于后续的坐标系转换非常重要。

接下来，我们需要确定目标坐标系。

gdal支持各种常见的地理坐标系和投影坐标系，如经纬度坐标系、UTM坐标系等。

根据实际需求，我们可以选择合适的目标坐标系进行转换。

在进行坐标系转换时，gdal提供了一系列的函数和工具。

我们可以使用gdalwarp命令行工具，通过指定源文件和目标坐标系参数，来实现TIFF文件的坐标系转换。

例如，我们可以使用以下命令将一个名为input.tif的TIFF文件从WGS84坐标系（EPSG:4326）转换为UTM坐标系（EPSG:32650）：gdalwarp -s_srs EPSG:4326 -t_srs EPSG:32650 input.tif output.tif在上述命令中，-s_srs参数指定源坐标系，-t_srs参数指定目标坐标系，input.tif是源文件名，output.tif是输出文件名。

除了命令行工具，gdal还提供了C++、Python等编程语言的API，可以通过编程的方式实现TIFF文件的坐标系转换。

通过gdal的API，我们可以读取TIFF文件的投影信息和地理坐标范围，创建坐标系转换的对象，并将转换后的数据写入新的TIFF文件。

总结一下，使用gdal进行TIFF转换坐标系的步骤如下：1. 了解原始TIFF文件的坐标系信息；2. 确定目标坐标系；3. 使用gdalwarp命令行工具或编程语言的API进行坐标系转换；4. 将转换后的数据写入新的TIFF文件。

arcgis空间数据的编辑处理及坐标变换实验3-1、空间数据库管理及属性编辑⼀、实验⽬的1. 利⽤ArcCatalog 管理地理空间数据库，理解Personal Geodatabse 空间数据库模型的有关概念。

2. 掌握在ArcMap中编辑属性数据的基本操作。

3. 掌握根据GPS数据⽂件⽣成⽮量图层的⽅法和过程。

4. 理解图层属性表间的连接(Join)或关联(Link)关系。

⼆、实验准备预备知识：ArcCatalog ⽤于组织和管理所有GIS 数据。

它包含⼀组⼯具⽤于浏览和查找地理数据、记录和浏览元数据、快速显⽰数据集及为地理数据定义数据结构。

基本概念：要素数据集、要素类数据⽂件：National.mdb ，GPS.txt （GPS野外采集数据）。

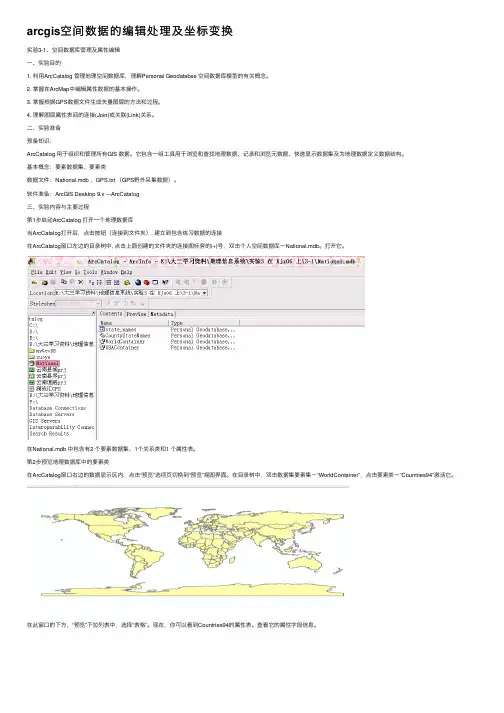
软件准备：ArcGIS Desktop 9.x ---ArcCatalog三、实验内容与主要过程第1步启动ArcCatalog 打开⼀个地理数据库当ArcCatalog打开后，点击按钮（连接到⽂件夹）. 建⽴到包含练习数据的连接在ArcCatalog窗⼝左边的⽬录树中, 点击上⾯创建的⽂件夹的连接图标旁的(+)号，双击个⼈空间数据库－National.mdb。

打开它。

在National.mdb 中包含有2 个要素数据集、1个关系类和1 个属性表。

第2步预览地理数据库中的要素类在ArcCatalog窗⼝右边的数据显⽰区内，点击“预览”选项页切换到“预览”视图界⾯。

在⽬录树中，双击数据集要素集－“WorldContainer”，点击要素类－“Countries94”激活它。

在此窗⼝的下⽅，“预览”下拉列表中，选择“表格”。

现在，你可以看到Countries94的属性表。

查看它的属性字段信息。

第3步创建缩图，并查看元数据导出元数据信息第4步创建个⼈地理数据库(Personal Geodatabase-PGD)在ArcCatalog 的⽬录树中，定位到E盘，右键点击这E盘，在出现的菜单中，选择[新建]>>[⽂件夹]，⽂件夹名称改为myGeoDB 。

实验六：空间数据的编辑处理及坐标变换一、实验目的意义1、掌握空间数据处理（融合、拼接、剪切、交叉、合并）的基本方法、原理，并领会其用途；2、掌握地图投影变换的基本原理与方法；3、熟悉ArcGIS中投影的应用及投影变换的方法、技术；4、了解地图投影及其变换在实际中的应用。

二、实验步骤实验准备：设定工作区：在ArcMap中执行菜单命令：<Tools>－><Options>，在“Geoprocessing”→“Environments…”→“General Setting”常规设置选项中，设定“Scratch Workspace”为d:\kGIS。

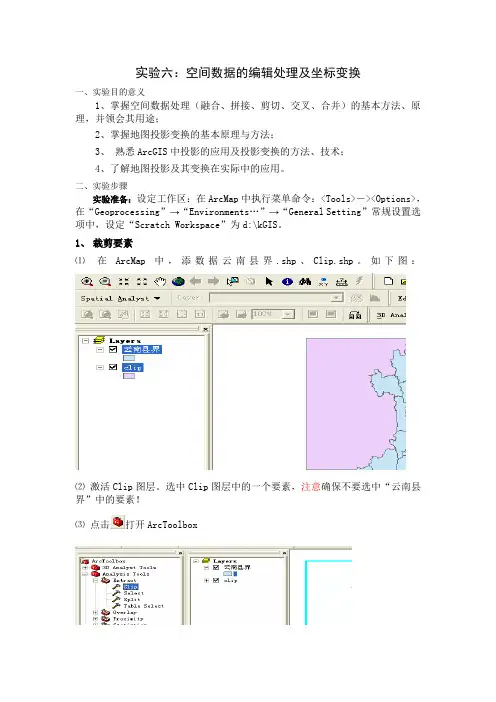
1、裁剪要素⑴在ArcMap中，添数据云南县界.shp、Clip.shp。

如下图：⑵激活Clip图层。

选中Clip图层中的一个要素，注意确保不要选中“云南县界”中的要素！⑶点击打开ArcToolbox⑷双击“Clip”选项，在弹出的对话框中设置：指定输出要素类路径及名称，这里请命名为“云南县界_Clip1”；指定输入类：云南县界；指定剪切要素：Clip（必须是多边形要素）。

在出现的选项框中填写相应内容，如下图：点击ok按钮后，剪切操作自动执行。

然后在TOC中关闭云南县界、Clip图层，就可看到剪切得到的结果。

⑸按照上述步骤，依次选中Clip主题中其它三个要素（三个矩形框），重复以上的操作步骤，完成操作后将得到共四个图层（“云南县界_Clip1”、“云南县界_Clip2”、“云南县界_Clip3”、“云南县界_Clip4”）。

选定1个要素4个要素都选定之后2、拼接图层⑴在ArcMap中新建地图文档，加载剪切要素操作（上一步）中得到的四个图层。

⑵打开ArcToolbox，在ArcToolbox中执行“Append”命令。

⑶在弹出的对话框中设置：输出要素设定为云南县界_Clip,输入要素依次添加其它三个图层。

如下图1图1 图2通过以上操作我们就完成了将4个图层拼接为一个图层的处理（如图2）。

gdal中转换坐标系GDAL（Geospatial Data Abstraction Library）是一个开源的地理空间数据处理库，提供各种功能用于读取、写入和转换各种常见的地理空间数据格式。

在实际的GIS应用中，常常需要将地理数据从一个坐标系转换为另一个坐标系，以满足不同的需求。

在这篇文章中，我们将一步一步介绍如何使用GDAL来进行坐标系转换。

第一步，安装GDAL库和相关依赖项。

GDAL可以在Linux、Windows 和Mac等操作系统上运行，并支持各种编程语言，如Python、C++和Java等。

你可以从GDAL的官方网站（第二步，了解地理数据的坐标系。

在进行坐标系转换之前，我们需要了解待转换的地理数据的坐标系信息。

常见的坐标系包括经纬度坐标系（如WGS84）和投影坐标系（如UTM）。

通过查看地理数据的元数据信息，我们可以获取到这些信息。

第三步，使用GDAL命令行工具进行坐标系转换。

GDAL提供了一系列命令行工具，可以直接在终端中使用。

其中，最常用的命令是`gdalwarp`。

首先，我们需要使用`gdalinfo`命令获取待转换地理数据的信息。

例如，执行以下命令可以查看一个GeoTIFF格式的影像数据的信息：gdalinfo input.tif在输出信息的最后，你可以找到地理数据的坐标系信息，如地理坐标系的名称、投影坐标系的名称和EPSG代码等。

下一步，使用`gdalwarp`命令进行坐标系转换。

例如，我们将一个WGS84坐标系的地理数据转换为UTM投影坐标系，可以执行以下命令：gdalwarp -s_srs EPSG:4326 -t_srs EPSG:32618 input.tif output.tif其中，`-s_srs`参数指定原始地理数据的坐标系，`-t_srs`参数指定目标坐标系，`input.tif`和`output.tif`分别是输入和输出的文件名。

第四步，使用GDAL库进行坐标系转换。

大地坐标与直角空间坐标转换计算公式一、参心大地坐标与参心空间直角坐标转换1名词解释：A ：参心空间直角坐标系：a) 以参心0为坐标原点；b) Z 轴与参考椭球的短轴（旋转轴）相重合；c) X 轴与起始子午面和赤道的交线重合；d) Y 轴在赤道面上与X 轴垂直.构成右手直角坐标系0-XYZ ；e) 地面点P 的点位用（X.Y.Z ）表示；B ：参心大地坐标系：a) 以参考椭球的中心为坐标原点.椭球的短轴与参考椭球旋转轴重合；b) 大地纬度B ：以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ；c) 大地经度L ：以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L ；d) 大地高H ：地面点沿椭球法线至椭球面的距离为大地高H ；e) 地面点的点位用（B.L.H ）表示。

2 参心大地坐标转换为参心空间直角坐标：⎪⎭⎪⎬⎫+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2公式中.N 为椭球面卯酉圈的曲率半径.e 为椭球的第一偏心率.a 、b 椭球的长短半径.f 椭球扁率.W 为第一辅助系数ab a e 22-= 或 ff e 1*2-= Wa N B W e =-=22sin *1( XX80椭球参数：长半轴a=6378140±5（m ）短半轴b=6356755.2882m扁 率α=1/298.2573 参心空间直角坐标转换参心大地坐标 []N BY X H H e N Y X H N Z B XY L -+=+-++==cos ))1(**)()(*arctan()arctan(22222 二 高斯投影及高斯直角坐标系1、高斯投影概述高斯-克吕格投影的条件：1. 是正形投影；2. 中央子午线不变形高斯投影的性质：1. 投影后角度不变；2. 长度比与点位有关.与方向无关；3. 离中央子午线越远变形越大为控制投影后的长度变形.采用分带投影的方法。

空间大地坐标系与平面直角坐标系转换公式空间大地坐标系和平面直角坐标系是两种不同的坐标系统，用于描述地球上的点的位置。

在进行空间大地坐标系与平面直角坐标系之间的转换时，需要考虑到地球的椭球体形状和投影方式。

下面将详细介绍空间大地坐标系与平面直角坐标系的转换方法。

1.空间大地坐标系经度：经度是指地球上特定点与本初子午线之间的角度差，用度、分、秒的形式表示。

纬度：纬度是指地球上特定点距离赤道的角度，用度、分、秒的形式表示。

大地高：大地高是指地球表面特定点到参考椭球体上其中一参考面的高度差，可分为正高和负高。

2.平面直角坐标系平面直角坐标系是以地球上一些基准点为原点建立的二维坐标系。

在平面直角坐标系下，点的位置通常用东方向坐标值X和北方向坐标值Y来表示。

3.空间大地坐标系到平面直角坐标系的转换公式3.1平面直角投影平面直角投影是将地球表面上的点投影到一个水平的平面上。

其转换公式为：X = k₀ + R * cosL * sin(λ - λ₀)Y = k₀ + R * (cosφ₀ * sinL - sinφ₀ * cosL * cos(λ - λ₀))其中，X和Y为平面直角坐标系下的坐标值，L为参考点与待转换点的经度差，λ为待转换点的经度，φ₀为参考点的纬度，λ₀为参考点的经度，k₀为常数，R为参考点到地心的距离。

3.2高斯投影高斯投影是将地球上的点投影到一个平面上，使得该平面上的距离尽可能与大地距离一致。

其转换公式为：X = X₀ + N * cosB * (λ - L₀)Y = Y₀ + N * (tanB * cos(λ - L₀) - sinB * (B - B₀))其中，X和Y为平面直角坐标系下的坐标值，X₀和Y₀为参考点的平面坐标，N为法向子午线长度，B为待转换点的纬度，λ为待转换点的经度，L₀为参考点的经度，B₀为参考点的纬度。

4.平面直角坐标系到空间大地坐标系的转换公式平面直角坐标系到空间大地坐标系的转换公式为空间大地坐标系到平面直角坐标系的逆运算，可以通过解方程组或迭代法来进行计算。

空间数据的坐标变换空间数据坐标变换的实质是建立两个平面点之间的一一对应关系，包括几何纠正和投影转换，它们是空间数据处理的基本内容之一。

对于数字化地图数据，由于设备坐标系与用户确定的坐标系不一致，以及由于数字化原图图纸发生变形等原因，需要对数字化原图的数据进行坐标系转换和变形误差的消除。

有时，不同来源的地图还存在地图投影与地图比例尺的差异，因此，还需要进行地图投影的转换和地图比例尺的统一（图3一1）。

1.1几何纠正几何纠正是为了实现对数字化数据的坐标系转换和图纸变形误差的改正。

现有的几种商业GIS软件一般都具有仿射变换、相似变换、二次变换等几何纠正功能。

仿射变换与相似变换相比较，前者是假设地图因变形而引起的实际比例尺在／和Y方向上都不相同，因此，具有图纸变形的纠正功能。

(X＝ao＋a,x＋a2Y、VI‘（3一2）’TlY＝b,＋b，x＋b2Y．Y,式（3一2）含有6个参数a。

、a，、a。

、b。

、b．、｝＼ｂＺ，要实现仿射变换，需要知道不在同一直I＼／／‘线上的3对控制点的数字化坐标及其理论ｌ入／《值，才能求得上述6个待定参数。

但在实际！叫应用中，通常利用4个以上的点来进行几何口匕一一一一一一匕‘一一一一一一今ｘ纠正。

下面按最小二乘法原理来求解待定参数：图3一2坐标变换原理设Qs、Q，表示转换坐标与理论坐标之差，则有f 0_＝X一（a-＋a，x＋a.,，）t ((，＝r一} Do＋。

,x＋b2Y）按照〔口几」＝min和「ｅ互」＝min的条件，可得到两组法方程：ra-n＋a，又x＋a,又，二又x、a-,.x十a, J x十a., }, x．v＝Lx．A (i＿4）Ｌ～、、．，．～、，．，．‘，＿灰，2＿又，＿。

v“ao山y十a,山x‘y＋a2山y＝山y’入和f bo n＋b, E x＋b2zy＝}Y（boLx＋b．Z; x`＋b2Zx·y＝Z x·Y（3一5）‘b,艺y＋b,名x"y＋b2艺厂二习Y- Y式中：n为控制点个数；二,y为控制点的数字化坐标；x、Y为控制点的理论坐标。

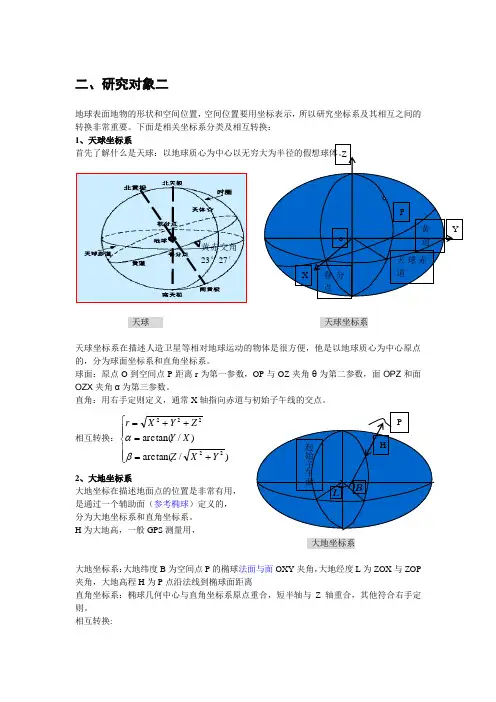
二、研究对象二地球表面地物的形状和空间位置，空间位置要用坐标表示，所以研究坐标系及其相互之间的转换非常重要。

下面是相关坐标系分类及相互转换： 1、天球坐标系首先了解什么是天球：以地球质心为中心以无穷大为半径的假想球体。

天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便，他是以地球质心为中心原点的，分为球面坐标系和直角坐标系。

球面：原点O 到空间点P 距离r 为第一参数，OP 与OZ 夹角θ为第二参数，面OPZ 和面OZX 夹角α为第三参数。

直角：用右手定则定义，通常X 轴指向赤道与初始子午线的交点。

相互转换：⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用， 是通过一个辅助面（参考椭球）定义的， 分为大地坐标系和直角坐标系。

H 为大地高，一般GPS 测量用，大地坐标系大地坐标系：大地纬度B 为空间点P 的椭球法面与面OXY 夹角，大地经度L 为ZOX 与ZOP 夹角，大地高程H 为P 点沿法线到椭球面距离直角坐标系：椭球几何中心与直角坐标系原点重合，短半轴与Z 轴重合，其他符合右手定则。

相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径，其中3、惯性坐标系（CIS ）与协议天球坐标系① 惯性坐标系（CIS ）:在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系：以某一约定时刻t0作为参考历元，把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴，以对应的春分点为X 轴的指向点，以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。

七参数空间直角坐标系坐标转换七参数空间直角坐标系坐标转换是一种用于坐标变换的方法，适用于不同坐标系统之间的几何空间数据转换。

该方法通过使用七个参数，将一个空间直角坐标系的坐标值转换为另一个空间直角坐标系的坐标值。

下面我将详细介绍七参数空间直角坐标系坐标转换的原理和步骤。

首先，我们需要了解各个参数的含义。

七参数包括三个平移参数(dx、dy、dz)，三个旋转参数(rx、ry、rz)，以及一个尺度参数(s)。

这些参数被用来描述两者之间的相对位移、旋转和尺度差异。

在进行坐标转换之前，我们需要确定参考坐标系和待转换坐标系之间的关系。

通常，一个参考点在两个坐标系之间进行观测，并且由以参考点为中心的变换可以表示为：X'=s(R*(X-T))其中，X'是待转换坐标系中的坐标，X是参考坐标系中的坐标，s是尺度因子，R是旋转矩阵，T是平移矩阵。

接下来，我们需要通过一组已知的点对来确定这七个参数的值。

通常情况下，我们至少需要三对已知点来确定平移参数和尺度参数；当需要考虑旋转参数时，通常需要更多的已知点对。

这些已知点对可以通过GNSS观测、GNSS/INS组合观测、摄影测量等手段来获取。

一旦我们确定了这七个参数的值，就可以使用它们来进行坐标转换了。

转换的步骤如下：1. 对于待转换的每一个坐标点(X, Y, Z)，将其减去参考点的坐标得到(dx, dy, dz)。

2. 根据旋转参数(rx, ry, rz)，计算旋转矩阵R。

3.计算变换矩阵R*(X-T)得到(X',Y',Z')。

4.使用尺度参数s来调整坐标(X',Y',Z')。

5. 将(X', Y', Z')加上平移参数(dx, dy, dz)得到最终的转换坐标。

需要注意的是，七参数空间直角坐标系转换是一种近似转换方法，它基于一些假设和简化，如刚体变换、平行投影等。

在实际应用中，可能会存在一定的误差。

第36卷第4期2027年12月测绘标准化Standardization of Surveying and MappingVoi-36No.4Doc-2027国上资源空间数据向2000国家大地坐标系转换方法探讨陆平(辽宁省自然资源事务服务中心辽宁省基础测绘院辽宁锦州121000)A Method Is Trvnsform Spatiai Data ot Nationai Land Reseurces Is CGCS2000LU Ping摘要：目前，国家启动了自然空间数据向2200国家大地坐标转换的工作，如何获取高精度、无损失的2200国家大地坐标系转换成果是目前迫切需要解决的问题。

以辽宁省某市2000国家大地坐标系转换项目为例，针对传统转换方法存在的不足，探讨应用高分辨率、高精度坐标转换格网进行控制点数据、矢量数据、栅格数据3种数据类型的坐标转换方法，提出3种数据转换的技术流程，并对3种数据的转换精度进行检测。

结果表明，利用高分辨率、高精度格网获取的改正参数，对一、二等三角点进行坐标转换，转换成果能够满足国家标准规定的精度要求。

关键词：坐标转换;格网点改正;精度检测；质量控制Keywcrdt:Cooreina)e Transformation；Grin Poigt Cofection；Acchrpce Testing；Qualita Control中图法分类号:P222.32200国家大地坐标系是我国自主构建的、符合国内现代空间科学技术要求的地心坐标系，从2208年7月1日开始，我国正式使用2700国家大地坐标系。

目前，我国启动了自然资源空间数据向2200国家大地坐标系转换的工作。

传统的坐标转换方法是将彳转换数据的每个坐标点作为转换中心，按照一定的搜索半径计算出该点进行转换所需要的重合点，进而获得该点位从原始坐标系向2700国家大地坐标系坐标转换的参数(dB,dL)，再通过参数改正获取该点的2700国家大地坐标系坐标。

大地坐标系与空间直角坐标系的相互转换方法1. 引言在测量和定位中，我们经常会用到坐标系来描述物体的位置。

大地坐标系和空间直角坐标系是常见的两种坐标系统，它们分别适用于地理测量和空间定位。

本文将介绍大地坐标系和空间直角坐标系之间的相互转换方法。

2. 大地坐标系大地坐标系是一种用来描述地球表面点位的坐标系统。

它采用经度、纬度和高度三个参数来确定点的位置。

2.1 经度和纬度经度是指地球表面上某点所在的东西方向线上的投影长度。

纬度是指地球表面上某点所在的南北方向线上的投影长度。

经度的取值范围是-180度到180度，纬度的取值范围是-90度到90度。

2.2 高度高度是指地球表面某点与平均海平面的距离。

它可以是正值，表示点位位于平均海平面之上，也可以是负值，表示点位位于平均海平面之下。

3. 空间直角坐标系空间直角坐标系是一种用来描述物体在空间中位置的坐标系统。

它采用直角坐标表示物体的位置，即用X、Y、Z三个参数表示点在空间中的位置。

3.1 X、Y、Z坐标X坐标表示点在东西方向上的位置，Y坐标表示点在南北方向上的位置，Z坐标表示点在垂直方向上的位置。

4. 大地坐标系转换为空间直角坐标系将大地坐标系中的经度、纬度和高度转换为空间直角坐标系中的X、Y、Z坐标，可以采用以下公式：X = (N + h) * cos(φ) * cos(λ)Y = (N + h) * cos(φ) * sin(λ)Z = (N * (1 - e^2) + h ) * sin(φ)其中，N为椭球面半径，h为高度，φ为纬度，λ为经度，e为第一偏心率。

5. 空间直角坐标系转换为大地坐标系将空间直角坐标系中的X、Y、Z坐标转换为大地坐标系中的经度、纬度和高度，可以采用以下公式：φ = atan(Z / sqrt(X^2 + Y^2))λ = atan(Y / X)h = sqrt(X^2 + Y^2 + Z^2) - N其中，N为椭球面半径，φ为纬度，λ为经度，h为高度。

大地坐标系与空间直角坐标系的相互转换公式概述大地坐标系和空间直角坐标系是地理信息系统中两种常用的坐标系。

大地坐标系主要用于描述地球上点的位置，而空间直角坐标系则是使用笛卡尔坐标系的三维空间中的坐标来表示点的位置。

在地理信息系统中，需要经常进行大地坐标系和空间直角坐标系之间的转换，以便在不同的坐标系统之间进行数据交互和分析。

大地坐标系大地坐标系是一种基于地球椭球体的坐标系统，常用来描述地球上点的位置。

一般采用经度（longitude）、纬度（latitude）和高程（elevation）来表示点在地球表面的位置。

经度表示点在东经或西经的位置，纬度表示点在北纬或南纬的位置，高程表示点相对于海平面的高度。

大地坐标系中经度的表示方式有多种，常见的有度分秒制和十进制制。

而纬度则一般用度制表示。

对于高程的表示方式，通常使用米作为单位。

空间直角坐标系空间直角坐标系是使用笛卡尔坐标系的三维空间中的坐标来表示点的位置。

在空间直角坐标系中，每个点的位置由三个数值组成，分别表示点在X轴、Y轴和Z轴方向上的位置。

这三个数值通常以米为单位。

空间直角坐标系中的原点可以选择任意位置，常见的有地心、地心地固、地心地独立三种坐标系。

地心坐标系以地球质心为原点，地心地固坐标系以地球上某一固定点为原点，地心地独立坐标系则是相对于地轴的一个旋转坐标系。

大地坐标系到空间直角坐标系的转换将大地坐标系中的点转换为空间直角坐标系中的点需要使用转换公式。

常用的转换方法有大地测量学和地心测量学两种。

### 大地测量学方法大地测量学方法中，将地球近似为椭球体，利用椭球体的形状参数和点的大地坐标来进行转换。

该方法的核心思想是通过计算点在曲线面上的法线方向，将大地坐标系的点转换为空间直角坐标系的点。

### 地心测量学方法地心测量学方法中，将地球近似为球体，并以地球质心或地球上某一固定点为原点。

该方法利用球面三角学的原理，根据点的经纬度和高程来进行转换。