高中物理 波的传播的多解性 (提纲、例题、练习、解析)

波传播的周期性和多解性问题1 •波动问题多解的主要因素⑴周期性①时间周期性：时间间隔A与周期T的关系不明确.②空间周期性：波传播的距离Ax与波长2的关系不明确.(2)双向性①传播方向双向性：波的传播方向不确定.②振动方向双向性：质点振动方向不确左.2.解决波的多解问题的思路一般采用从特殊到一般的思维方法，即找岀一个周期内满足条件的关系$或Ax，若此关系为时间,则尸“T+A("=O丄2,…)：若此关系为距离，贝!jx=m+W=0,12，…).【例4】一简谐横波在均匀介质中沿水平方向直线传播，/、E为介质中的两个质点，其振动(1)该简谐横波传播速度的可能值：(2)若改变波源的振动频率，使A. B两质点的振动同步，求频率的可能值. 答案(1)°=»打m/'s(n=0,l,2,…)(2尸 J：、Hz (ii=Q,1,2,…，加= 1,2,3,…)解析(1)由图象可知，该简谐波的周期T=4 sx=(2卄1£ (77=0,1,2,…)设传播速皮为V,则有y=y解得该简谐横波传播速度的可能值◎=2”； 1 也.("=0,1,2,…)(2)设波源振动频率为/；则有x=mV (加= 123 …)v=A r f解得频率的可能值Hz (”=0,1,2,…，加= 1,2,3,…)。

题组阶梯突破5.(2015•课标I 34(2))甲、乙两列简谐横波在同一介质中分别沿x轴正向和负向传播，波速均为0=25 cm/s.两列波在/=0时的波形曲线如图10所示.求：(1)r=0时，介质中偏离平衡位置位移为16 cm的所有质点的x坐标：(2)从『=0开始，介质中最早出现偏离平衡位宜位移为一 16 cm的质点的时间.答案(l)x=(5O+3OO〃)cm (M=0, ±1, ±2, ±3,…)(2)0.1 s解析(1)两列波的振幅均为8 cm,故倔离平衡位置位移为16 cm的质点应为两列波的波峰相遇处的质点.根据波形图可知，甲、乙的波长分别为2 c=60 cm,几甲=50 cm则甲、乙两列波的波峰x坐标分别为x.=(5O+hX5O)cm 伙i = 0, ±1, ±2, ±3,…)x 乙=(50+hX60)cm 伙2=0, ±1, ±2, ±3,…)综上分析，所有波峰和波峰相遇的质点x坐标应为x=(50+300w) cm (w=0, ±1,±2, ±3,…)⑵偏离平衡位置位移为一 16 cm对应为两列波的波谷相遇・『=0时，波谷之差Ax=(50+^^X60)_(50+^^X50)整理可得山=10(6〃1一5肥)+5波谷之间置小的距离为Ax' =5 cm两列波相向传播,相对速度为2u=50cm/s所以出现偏离平衡位置位移为一16 cm的最短时间r=^-=O.ls.6.有两列简谐横波a、b在同一介质中分别沿x轴正方向和负方向传播.两列波在r=0时刻的波形曲线如图11所示，已知d波的周期几=ls・求：(1)两列波的传播速度：⑵从尸0时刻开始，最短经过多长时间x=1.0 m的质点偏离平衡位置的位移为0.161^答案(1)2.5 m/s (2)5.4 s 解析(1)由图可知心b两列波的波长分别为為=2.5 m,几=4.0 m两列波在同种介质中的传播速度相同为V=jr=2.5m/s(2)。

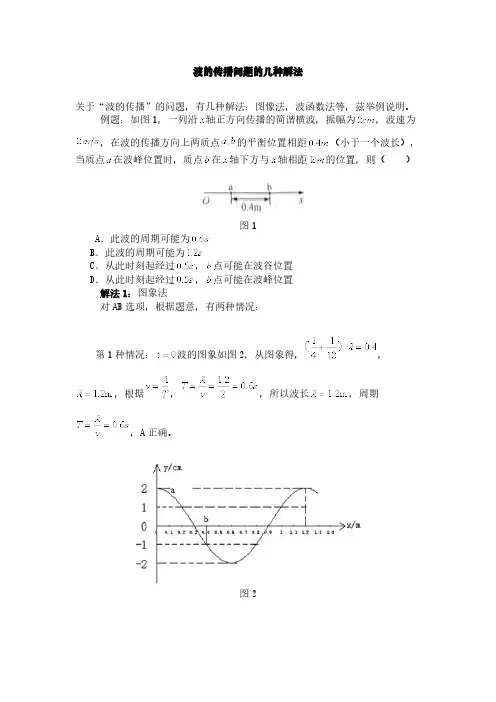
波的传播问题的几种解法关于“波的传播”的问题，有几种解法：图像法，波函数法等，兹举例说明。

例题：如图1，一列沿轴正方向传播的简谐横波，振幅为，波速为，在波的传播方向上两质点的平衡位置相距（小于一个波长），当质点在波峰位置时，质点在轴下方与轴相距的位置，则（ ）图1 A．此波的周期可能为　B．此波的周期可能为　C．从此时刻起经过，点可能在波谷位置　D．从此时刻起经过，点可能在波峰位置 解法1：图象法 对AB选项，根据题意，有两种情况： 第1种情况：波的图象如图2，从图象得，，，根据，，所以波长，周期，A正确。

图2第2种情况：波的图象如图3，从图象得，，，根据，，所以，波长，周期。

图3 因为只有以上两种情况，所以B错误。

对CD选项，根据以上两种情况，也有两种有两种对应的情况： 第1种情况：波长是的波，在波的图象如图4，从图象知，b在波谷，所以C正确。

图4 第2种情况，波长是的波，波的图象如图5，从图象知，的在波峰，所以D正确。

图5 综上各图，所以本题选ACD。

解法2：波函数法 （1）波函数的定义 为了定量地描述介质中波动的情况，必修求得介质中各质元的位移与该质元所处的平衡位置及时间的定量关系，这种定量关系就是波的表达式，也叫做波函数（wave function）。

（2）简谐波函数的推导 设有一波前为平面的简谐波，在均匀介质中沿轴正方向传播，波速为。

由于这是一种平面波，所以在与轴垂直的平面上，各点的振动情况是一样的。

所以只要讨论轴上各点的振动，就可以知道空间中各点的情况。

以O点为波源，设该处质元做简谐振动，其位移与时间的关系为 式中A为振幅，为角频率。

考察波线O上的任一点P，它离O点的距离为，当波源O的振动传到P点时，P点的质元将重复O点的质元的振动，角频率也相同，但振动的相位要落后于O点。

因为O点的振动传到P点需要时间，所以P处质元在时刻的振动相位和O点质元在时刻的振动相位一样，即其相位为（ ） 因为平面简谐波传播时各质元的振幅相等，P处质元在时刻的位移为 ，这就是平面简谐波的波函数。

波的传播问题的几种解法关于“波的传播”的问题，有几种解法：图像法，波函数法等，兹举例说明。

例题：如图1，一列沿轴正方向传播的简谐横波，振幅为，波速为，在波的传播方向上两质点的平衡位置相距（小于一个波长），当质点在波峰位置时，质点在轴下方与轴相距的位置，则（）图1A．此波的周期可能为B．此波的周期可能为C．从此时刻起经过，点可能在波谷位置D．从此时刻起经过，点可能在波峰位置解法1：图象法对AB选项，根据题意，有两种情况：第1种情况：波的图象如图2，从图象得，，，根据，，所以波长，周期，A正确。

图2第2种情况：波的图象如图3，从图象得，，，根据，，所以，波长，周期。

图3因为只有以上两种情况，所以B错误。

对CD选项，根据以上两种情况，也有两种有两种对应的情况：第1种情况：波长是的波，在波的图象如图4，从图象知，b在波谷，所以C正确。

图4第2种情况，波长是的波，波的图象如图5，从图象知，的在波峰，所以D正确。

图5综上各图，所以本题选ACD。

解法2：波函数法（1）波函数的定义为了定量地描述介质中波动的情况，必修求得介质中各质元的位移与该质元所处的平衡位置及时间的定量关系，这种定量关系就是波的表达式，也叫做波函数（wave function）。

（2）简谐波函数的推导设有一波前为平面的简谐波，在均匀介质中沿轴正方向传播，波速为。

由于这是一种平面波，所以在与轴垂直的平面上，各点的振动情况是一样的。

所以只要讨论轴上各点的振动，就可以知道空间中各点的情况。

以O点为波源，设该处质元做简谐振动，其位移与时间的关系为式中A为振幅，为角频率。

考察波线O上的任一点P，它离O点的距离为，当波源O的振动传到P点时，P点的质元将重复O点的质元的振动，角频率也相同，但振动的相位要落后于O点。

因为O点的振动传到P点需要时间，所以P处质元在时刻的振动相位和O点质元在时刻的振动相位一样，即其相位为（）因为平面简谐波传播时各质元的振幅相等，P处质元在时刻的位移为，这就是平面简谐波的波函数。

波的多解问题一、波传播的周期性与多解问题1．造成波传播多解的主要因素(1)周期性①时间周期性：时间间隔Δt 与周期T 的关系不明确。

②空间周期性：波传播的距离Δx 与波长λ的关系不明确。

(2)双向性①传播方向双向性：波的传播方向不确定。

②振动方向双向性：质点振动方向不确定。

2．解决波的多解问题的思路一般采用从特殊到一般的思维方法，即找出一个周期内满足条件关系的Δt 或Δx ，若此关系为时间，则t ＝nT ＋Δt (n ＝0，1，2，…)；若此关系为距离，则x ＝nλ＋Δx (n ＝0，1，2，…)。

二、针对练习1、（多选）一列在竖直方向振动的简谐横波，波长为λ，沿正x 方向传播.某一时刻，在振动位移向上且大小等于振幅一半的各点中，任取相邻的两点1P 、2P ，已知1P 的x 轴坐标小于2P 的x 轴坐标，则（ ）A ．若221λ<P P ，则1P 向下运动，2P 向上运动 B ．若221λ<P P ，则1P 向上运动，2P 向下运动 C ．若221λ>P P ，则1P 向上运动，2P 向下运动 D ．若221λ>P P ，则1P 向下运动，2P 向上运动2、(多选)如图所示，一列简谐横波沿x 轴传播，实线为t ＝0时的波形图，虚线为t ＝0.5 s 时的波形图，下列说法正确的是( )A ．若波沿x 轴正方向传播，则其最大周期为2.0 sB ．若波沿x 轴负方向传播，则其传播的最小速度为2 m/sC ．若波速为26 m/s ，则t ＝0时P 质点的运动方向沿y 轴正方向D ．若波速为14 m/s ，则t ＝0时P 质点的运动方向沿y 轴正方向3、（多选 ）一列横波以10 m/s 的速率沿水平方向传播，某时刻的波形如图中的实线所示，经时间t ∆后的波形如图中的虚线所示，已知T t T >∆>2(T 为这列波的周期).由此可知t ∆可能是（ ）A ．0.3sB ．0.5sC ．0.6sD ．0.7s4、(多选)一列简谐横波沿x 轴传播，t ＝0时刻该波波形如图中实线所示，此时x ＝0处的质点沿y 轴负向振动；t ＝2.0 s 时刻波形如图中虚线所示。

波的图象多解问题【思考】１．波动图象多解问题主要由两方面引起：①波图象的周期性；②波传播方向的双向性。

２．由于波的周期性和波的传播方向的不明确导致波动问题中出现系列解、多解问题，主要包括三种情况：① 时间间隔Δt 与周期T 的关系不明确② 波传播的距离Δx 与波长λ的关系不明确③ 传播方向的不明确【预测】1．一列横波沿直线在介质中传播，某时刻直线上相距s 的a 、b 两点均处在平衡位置，如图所示，若a 、b 之间只有一个波峰，且经过时间t 后质点b 第一次到达波峰位置，则这列波的波速可能是 （ ）A ．t sB ．t s t s 232和C ．t s t s 434和D ．ts t s 636和 2．有一列沿水平绳传播的简谐横波，频率为10Hz ，振动方向沿竖直方向，当绳上的质点P 到达其平衡位置且向下运动时，在其右方相距0.6m 处的质点Q 刚好到达最高点。

由此可知波速和传播方向可能是 （ ）A ．8m/s ，向右传播B ．8m/s ，向左传播C ．24m/s ，向右传播D ．24m/s ，向左传播3．一列横波在t =0时刻的波形如图中实线所示，在t =1s 时刻的波形如图中虚线所示。

由此可以判定此波的 （ ）A ．波长一定是4cmB ．周期一定是4sC ．振幅一定是2cmD ．传播速度一定是1cm/s4．一列沿x 轴正方向传播的简谐横波，周期为0.5s ；某一时刻，离开平衡位置的位移都相等的各质点依次为P 1、P 2、P 3···已知P 1和P 2之间的距离为20cm ，P 2和P 3之间的距离为80cm ，则P 1的振动传到P 2所需要的时间为 （ ）A ．0.50sB ．0.13sC ．0.10sD ．0.20s5．一列简谐横波沿x 轴正方向传播，x 轴上相距 1.2m 的两个质点A 和B ，它们的振动方向始终是相反的，已知波的周期是0.2s ，则这列波的波速多大？【例题】6．如图所示，一根张紧的水平弹性长绳上的a 、b 两点，相距14m ，b 点在a 点的右方；当一列简谐横波沿此长绳向右传播时，若a 点的位移达到正的最大时，b 点的位移恰好为零，且向下运动；经过1s 后，a 点的位移为零，且向下运动，而b 点的位移恰好达到负最大，则这列简谐横波的波速可能等于 （ ）A ．4.67m/sB ．6.0m/sC ．10.0m/sD ．14.0m/s7．在波的传播方向上，有相距1.05m 的两质点a 、b ，当a 到达正向最大位移时，b 恰好在平衡位置，已知a 、b 间的距离小于２个波长，波的频率为200Hz ，求波传播的可能速度。

2.4 波的多解问题1．造成波动问题多解的主要因素(1)周期性：①时间周期性：时间间隔Δt与周期T的关系不明确。

②空间周期性：波传播距离Δx与波长λ的关系不明确。

(2)双向性：①传播方向双向性：波的传播方向不确定。

②振动方向双向性：质点振动方向不确定。

如：a.质点达到最大位移处，则有正向和负向最大位移两种可能。

b．质点由平衡位置开始振动，则起振方向有向上、向下(或向左、向右)两种可能。

c．只告诉波速不指明波的传播方向，应考虑沿两个方向传播的可能，即沿x轴正方向或沿x轴负方向传播。

d．只给出两时刻的波形，则有多次重复出现的可能。

(3)波形的隐含性形成多解：在波动问题中，往往只给出完整波形的一部分，或给出几个特殊点，而其余信息均处于隐含状态。

这样，波形就有多种情况，形成波动问题的多解性。

2．解决波的多解问题的思路一般采用从特殊到一般的思维方法，即找出一个周期内满足条件的关系Δt或Δx，若此关系为时间，则t＝nT＋Δt(n＝0，1,2…)；若此关系为距离，则x＝nλ＋Δx(n＝0,1，2…)。

1.时间的多解问题例1．一列简谐横波在x轴上传播，如图4所示，实线是这列波在t1＝0.1 s 时刻的波形，虚线是这列波在t 2＝0.2 s 时刻的波形，求：图4(1)如果此波沿x 轴正方向传播，波速的最小值；(2)如果此波沿x 轴负方向传播，波速的可能值．答案 (1)30 m/s (2)v ＝(80k ＋50) m/s(k ＝0,1,2，3…)解析 (1)由波形图知波长λ＝8 m波沿x 轴正方向传播时，传播距离Δx 满足Δx ＝kλ＋38λ(k ＝0,1,2,3…)由v ＝Δx Δt 知，当k ＝0时波速取最小值．解得最小波速v min ＝30 m/s(2)波沿x 轴负方向传播时，传播距离Δx ＝kλ＋58λ(k ＝0,1,2,3…)由v ＝Δx Δt 得v ＝(80k ＋50) m/s(k ＝0,1,2,3…)1.一列简谐横波在x 轴上传播，在t 1＝0和t 2＝0.05 s 时刻，其波形图分别如图中的实线和虚线所示，求：(1)该波的振幅和波长；(2)若这列波向右传播，波速是多少？若这列波向左传播，波速是多少？解析：(1)由图可知：A ＝2 cm ，λ＝8 m(2)若波向右传播，则Δx 1＝14λ＋nλ＝2＋8n (n ＝0,1,2，…)v 1＝Δx 1Δt ＝2＋8n 0.05＝40＋160n (n ＝0,1,2，…)若波向左传播，则Δ x 2＝34λ＋nλ＝6＋8n (n ＝0,1,2，…)v 2＝Δx 2Δt ＝6＋8n 0.05＝120＋160n (n ＝0,1,2，…)答案： (1)2 cm 8 m (2)40＋160n (n ＝0,1,2，…)，120＋160n (n ＝0,1,2，…)2．如图所示，实线是某时刻的波形图，虚线是0.2 s 后的波形图．(1)若波向左传播，求它的可能周期和最大周期；(2)若波向右传播，求它的可能传播速度；(3)若波速是45 m/s ，求波的传播方向．答案 (1)0.84n ＋3s(n ＝0,1,2，…) 0.27 s (2)5(4n ＋1) m/s(n ＝0,1,2，…) (3)向右解析 (1)波向左传播，传播的时间为Δt ＝34T ＋nT (n ＝0,1,2，…)，所以T ＝4Δt 4n ＋3＝4×0.24n ＋3 s ＝0.84n ＋3s(n ＝0,1,2，…)，最大周期为T max ＝0.83 s≈0.27 s.(2)波向右传播，Δt ＝T 4＋nT (n ＝0,1,2，…)所以T ＝0.84n ＋1s(n ＝0,1,2，…)，而λ＝4 m 所以v ＝λT ＝5(4n ＋1) m/s(n ＝0,1,2，…)．（3）波速是45 m/s ，设波向右传播，由上问求得的向右传播的波速公式得：45 m/s ＝5(4n ＋1) m/s ，解得n ＝2.故假设成立，因此波向右传播．例2．如图5所示，图中的实线是一列简谐横波在t ＝0时刻的波形图，虚线对应的是t ＝0.5 s 时的波形图．求：图5(1)如果波沿x 轴负方向传播，且周期T ＞0.5 s ，则波的速度多大？(2)如果波沿x 轴正方向传播，且周期T 满足0.3 s ＜T ＜0.5 s ，则波的速度又是多少？答案 (1)0.12 m/s (2)0.84 m/s解析 (1)如果波沿x 轴负方向传播，且周期T ＞0.5 s ，则波向左传播的距离x ＝14λ＝14×24 cm ＝6 cm波速v ＝x t ＝0.06 m 0.5 s ＝0.12 m/s(2)如果波是沿x 轴正方向传播的，且周期T 满足0.3 s ＜T ＜0.5 s ，则波向右传播了1个波长多，所以波传播的距离为x ＝34λ＋λ＝74×24 cm＝42 cm波速v ＝x t ＝0.42 m 0.5 s ＝0.84 m/s.1.如图所示实线是一列简谐横波在t 1＝0时刻的波形，虚线是这列波在t 2＝0.5 s 时刻的波形，这列波的周期T 符合：3T ＜t 2－t 1＜4T ，问：(1)若波速向右，波速多大？(2)若波速向左，波速多大？(3)若波速大小为74 m/s ，波速方向如何？[解析] (1)波向右传播时，传播距离Δx 满足Δx ＝kλ＋38λ(k ＝0,1,2,3…)由Δt ＝Δx v 知传播时间满足Δt ＝kT ＋38T (k ＝0,1,2,3…)由于3T ＜t 2－t 1＜4T因此k 取3故Δt ＝3T ＋38T由波形图知λ＝8 m波速v ＝λT解得v ＝54 m/s(2)波向左传播时，传播距离Δx 满足Δx ＝kλ＋58λ(k ＝0,1,2,3，…)传播时间满足Δt ＝kT ＋58T (k ＝0,1,2,3…)由3T ＜t 2－t 1＜4T 可知k 取3故Δt ＝3T ＋58T波速v ＝λT解得v ＝58 m/s(3)波速大小为74 m/s 时，波在Δt 时间内传播的距离为Δx ＝v Δt ＝74×0.5 m ＝37 m ＝(4λ＋5) m所以波向左传播[答案] (1)54 m/s (2)58 m/s (3)波向左传播2.(2019·绵阳三诊)如图所示，一简谐横波在t ＝0时的波形是图中实线，在t 1＝0.2 s 时的波形是图中虚线，P 为介质中x ＝4 m 处的质点，则( )A ．该波一定沿x 轴正方向传播B ．该波的传播速度可能为5 m/sC ．从t ＝0开始，质点P 经过0.2 s 沿x 轴正方向运动1 mD ．t ＝0.4 s 时，质点P 的位置y ＝4 cm[解析] 当波向左传播时，传播的距离x ＝nλ＋34λ＝4n ＋3,0.2＝nT ＋34T ，波速v ＝20n ＋15(m/s)，T ＝0.84n ＋3，n ＝0、1、2、3… 当波向右传播时，传播的距离x ＝nλ＋14λ＝4n ＋1,0.2＝nT ＋14T ，波速v ＝20n ＋5(m/s)，T ＝0.84n ＋1，n ＝0、1、2、3… 由于波传播方向的不定性，所以据波形图与时间无法判断该波的传播方向，故A 错误。

波的多解问题一、波的多解产生的原因由于波在时间及空间上的重复性，波在传播方向上有不确定性，故波的问题往往会引起多解，因此，在解决波的问题时，要特别注意是否有多解。

这类问题又往往与波形图联系在一起。

此类问题关键是要根据题意画出正确的波形图，而且必须考虑各种可能性。

1．传播方向不确定引起多解：波总是由波源发出并由近及远地向前传播。

波在介质中传播时，介质各质点的振动情况依据波的传播情况是可以确定的，反之亦然。

如果根据题目中中已知条件不能确定波的传播方向或者不能确定质点的振动方向，就会出现多解。

2．波在空间上的重复性引起多解：沿波的传播方向，距离相隔n(n=1,2,3,…)个波长的质点的振动情况是完全相同的，故波沿波的传播方向传播n(n=0、1、2……)个波长时，波形图与原来完全相同。

因此，当题目中波的传播时间与质点振动的周期的关系不确定，或波的传播距离与波长的关系不确定时，就会出现多解。

因此，在已知传播时间的情况下，应考虑传播时间是否已超过一个周期；在已知传播距离的情况下，应考虑传播距离是否已超过一个波长。

3．两质点间关系不确定形成多解：在波的传播方向上，如果两个质点间的距离不确定，就会形成多解。

二、例题分析例1、如图所示为一列横波在某时刻的波形图。

此时x=2m处的质点M恰好位于平衡位置，再经过0.1s，质点M到达y=2cm。

已知波的周期大于0.1s分析：由于波的周期大于0.1s，故波在0.1s内传播的距离必小于一个波长。

由M到达的新位置可以画出再过0.1s时的波形图如图。

由于不知道波的传播方向，也无法确定波的传播方向，故新的波形可能是原波形向右传播λ/4而形成的，也可能是-2原波形向左传播3λ/4而形成的。

这两种情况都是可能的。

故在解题时要分两种情况讨论。

解：由图可读出波长λ=4m。

1、若波向右传播，则依题意，在0.1s时间波传播了λ/4。

s=λ/4=1mv=s/t=1/0.1=10m/s2、若波向左传播，则依题意，则0.1s 的时波传播了3λ/4。