第三章 拉普拉斯变换法-3
- 格式:ppt
- 大小:1.11 MB
- 文档页数:12

拉普拉斯变换微分定理三阶一、拉普拉斯变换简介拉普拉斯变换是一种数学变换,它在数学、物理、工程等领域具有广泛的应用。
拉普拉斯变换源于法国数学家拉普拉斯在18世纪末的研究成果,它是一种将复杂数学问题简化求解的方法。
1.拉普拉斯变换的定义拉普拉斯变换是将一个函数f(t)变换为另一个函数F(s)的运算,定义如下:F(s) = ∫(e^(-st) * f(t) * dt),其中s为变换域变量,t为时域变量。
2.拉普拉斯变换的基本性质拉普拉斯变换具有以下基本性质:(1) 线性性质:拉普拉斯变换具有线性性质,即变换后的函数是原函数的线性组合。
(2) 尺度变换:拉普拉斯变换具有尺度变换性质,变换后的函数与变换前的函数在尺度上存在一定的关系。
(3) 移位性质:拉普拉斯变换具有移位性质,变换后的函数通过平移原函数得到。
二、拉普拉斯变换微分定理三阶的推导拉普拉斯变换微分定理是拉普拉斯变换在微分方程求解中的应用。
以下是拉普拉斯变换微分定理三阶的推导过程:1.拉普拉斯变换微分定理一阶设f(t)为t的函数,对其进行一阶导数,得到f"(t)。
将f(t)和f"(t)进行拉普拉斯变换,得到F(s)和F"(s)。
2.拉普拉斯变换微分定理二阶对拉普拉斯变换后的函数F"(s)进行一阶导数,得到F""(s)。
3.拉普拉斯变换微分定理三阶对拉普拉斯变换后的函数F""(s)进行一阶导数,得到F"""(s)。
三、拉普拉斯变换微分定理三阶的应用拉普拉斯变换微分定理三阶在求解微分方程、信号处理与系统分析、工程与应用等领域具有广泛的应用。
1.求解微分方程利用拉普拉斯变换微分定理三阶,可以将复杂微分方程转化为更易于求解的线性微分方程。
2.信号处理与系统分析拉普拉斯变换微分定理三阶在信号处理与系统分析中具有重要意义,可以帮助分析信号的频率特性和系统的稳定性。





目录第一章自动控制系统的基本原理第一节控制系统的工作原理和基本要求第二节控制系统的基本类型第三节典型控制信号第四节控制理论的内容和方法第二章控制系统的数学模型第一节机械系统的数学模型第二节液压系统的数学模型第三节电气系统的数学模型第四节线性控制系统的卷积关系式第三章拉氏变换第一节傅氏变换第二节拉普拉斯变换第三节拉普拉斯变换的基本定理第四节拉普拉斯逆变换第四章传递函数第一节传递函数的概念与性质第二节线性控制系统的典型环节第三节系统框图及其运算第四节多变量系统的传递函数第五章时间响应分析第一节概述第二节单位脉冲输入的时间响应第三节单位阶跃输入的时间响应第四节高阶系统时间响应第六章频率响应分析第一节谐和输入系统的定态响应第二节频率特性极坐标图第三节频率特性的对数坐标图第四节由频率特性的实验曲线求系统传递函数第七章控制系统的稳定性第一节稳定性概念第二节劳斯判据第三节乃奎斯特判据第四节对数坐标图的稳定性判据第八章控制系统的偏差第一节控制系统的偏差概念第二节输入引起的定态偏差第三节输入引起的动态偏差第九章控制系统的设计和校正第一节综述第二节希望对数幅频特性曲线的绘制第三节校正方法与校正环节第四节控制系统的增益调整第五节控制系统的串联校正第六节控制系统的局部反馈校正第七节控制系统的顺馈校正第一章自动控制系统的基本原理定义:在没有人的直接参与下,利用控制器使控制对象的某一物理量准确地按照预期的规律运行。
第一节控制系统的工作原理和基本要求一、控制系统举例与结构方框图例1.一个人工控制的恒温箱,希望的炉水温度为100C°,利用表示函数功能的方块、信号线,画出结构方块图。
图1人通过眼睛观察温度计来获得炉内实际温度,通过大脑分析、比较,利用手和锹上煤炭助燃。
比较图2例2.图示为液面高度控制系统原理图。
试画出控制系统方块图和相应的人工操纵的液面控制系统方块图。
解:浮子作为液面高度的反馈物,自动控制器通过比较实际的液面高度与希望的液面高度,调解气动阀门的开合度,对误差进行修正,可保持液面高度稳定。



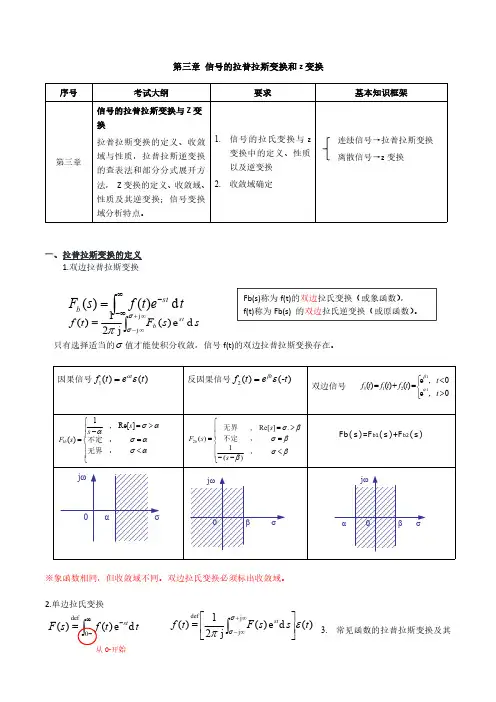
⎰∞∞--=t e t f s F st b d )()(⎰∞--=0def d e )()(t t f s F st)(d e )(j 21)(j j deft s s F t f st επσσ⎥⎦⎤⎢⎣⎡=⎰∞+∞-第三章信号的拉普拉斯变换和z 变换一、拉普拉斯变换的定义1.双边拉普拉斯变换只有选择适当的σ值才能使积分收敛,信号f(t)的双边拉普拉斯变换存在。
※象函数相同,但收敛域不同。
双边拉氏变换必须标出收敛域。
2.单边拉氏变换3.常见函数的拉普拉斯变换及其⎰∞+∞-=j j d e )(j21)(σσπs s F t f st b Fb(s)称为f(t)的双边拉氏变换(或象函数),f(t)称为Fb(s)的双边拉氏逆变换(或原函数)。
从0-开始收敛域二、拉普拉斯变换性质线性性质尺度变换证明:[]⎰∞--=de)()(tatfatf L st,则令atτ=时移特性与尺度变换相结合复频移(s域平移)特性时域的微分特性(微分定理)若f(t)←→F(s),Re[s]>σ0,则f’(t)←→sF(s)–f(0-)证明:()()()())(deedessFfttsft ftt f ststst+-=⎥⎦⎤⎢⎣⎡--='--∞-∞---∞-⎰⎰推广:()()[])0()0()()0(d)(d22----'--='--=⎥⎦⎤⎢⎣⎡fsfsFsffsF sttfL∑-=----=⎥⎦⎤⎢⎣⎡1)(1)0()(d)(d nrrrnnnfssFsttfL若f1(t)←→F1(s)Re[s]>σ1,f2(t)←→F2(s)Re[s]>σ2则a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)Re[s]>max(σ1,σ2)若f(t)←→F(s),Re[s]>σ0,且有实数a>0,则f(at)←→)(1asFa若f(t)<----->F(s),Re[s]>σ0,且有实常数t0>0,则f(t-t0)ε(t-t0)<----->e-st0F(s),Re[s]>σ0若f(t)←→F(s),Re[s]>σ0,且有复常数s a=σa+jΩa,则f(t)e s a t←→F(s-s a),Re[s]>σ0+σas-→2:?)(sin ←→t t t ε=三、拉普拉斯逆变换三种方法:(1)查表(2)利用性质(3)部分分式展开-----结合∴......,,321为不同的实数根,n p p p p nn p s K p s K p s K s F -++-+-= 2211)(ip s i i s F p s K =-=)()()(e ]1[1t p s L t p i i ε=--若象函数F(s)是s 的有理分式,可写为1110111.......)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=----若m ≥n (假分式),可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。

拉普拉斯变换公式拉普拉斯变换是一种常用于处理连续时间系统的数学工具,它将一个函数从时域(时间域)转换到频域(复频域),使得用复频率来研究连续时间系统变得更加方便。
拉普拉斯变换在信号处理、控制工程、通信系统等领域中都有广泛的应用。
设时域函数为f(t),其中0≤t≤∞,则其拉普拉斯变换为F(s),其中s为复变量。
拉普拉斯变换公式如下:F(s) = ∫[0,∞]f(t)e^(-st)dt通过拉普拉斯变换,我们可以将函数从时域转换到频域,可以得到函数在复频率域的频谱表示。
例如,对于一个连续时间系统的单位阶跃响应函数h(t),我们可以通过拉普拉斯变换将其变换为H(s),即H(s)=L[h(t)]。
1.时间平移定理:如果f(t)的拉普拉斯变换为F(s),则e^(at)f(t)的拉普拉斯变换为F(s-a)。
这个定理表示,如果时域函数f(t)右移或者左移a个单位,则其拉普拉斯变换在复频域中左移或者右移a个单位。
2.频率平移定理:如果f(t)的拉普拉斯变换为F(s),则e^(st)f(t)的拉普拉斯变换为F(s-a)。
这个定理表示,如果时域函数f(t)乘以指数函数e^(st),则其拉普拉斯变换在复频域中右移s个单位。
3.初值定理:如果f(t)的拉普拉斯变换为F(s),则f(0+)的值等于F(∞)。
这个定理表示,拉普拉斯变换函数在复频域中的极限为时域函数在时刻t=0+的值。
4.终值定理:如果f(t)的拉普拉斯变换为F(s),则lim(s→0)sF(s) =lim(t→∞)f(t)。
这个定理表示,拉普拉斯变换函数在复频域中的极限为时域函数在过去无限远到未来无限远的时刻t=∞处的值。
5.单位脉冲响应函数与系统频率响应函数的关系:设h(t)为系统的单位脉冲响应函数,即系统在输入为单位脉冲信号时的响应。
如果H(s)为系统的拉普拉斯变换,即H(s)=L[h(t)],则系统的频率响应函数为H(jω),即将变量s替换为jω,其中j为虚数单位,ω为频率。
拉普拉斯变换公式总结拉普拉斯变换是一种傅里叶变换的扩展,广泛应用于信号处理和控制系统的分析。
它将时间域中的函数转换到复平面的变换域中,可以有效地处理复杂的微分和积分方程。
拉普拉斯变换有许多重要的性质和公式,下面将对其中的一些进行总结。
1.拉普拉斯变换定义F(s) = L[f(t)] = ∫[0,∞) e^(-st) f(t) dt其中,s为复变量,t为时间,e为自然常数。
2.拉普拉斯变换的收敛条件要使拉普拉斯变换存在,函数f(t)必须满足一定的收敛条件。
常见的收敛条件为:函数f(t)是因果(即f(t)在t<0时为零)和指数增长边界条件(即函数f(t)e^(-αt)在t趋于正无穷时有界)。
3.常见的拉普拉斯变换公式3.1常函数的拉普拉斯变换:L[1]=1/s3.2单位阶跃函数的拉普拉斯变换:L[u(t)]=1/s3.3单位冲激函数的拉普拉斯变换:L[δ(t)]=13.4指数函数的拉普拉斯变换:L[e^(at)] = 1/(s-a),其中a为常数3.5高斯函数的拉普拉斯变换:L[e^(-at^2)] = sqrt(π/a) × e^(s^2/4a)3.6正弦和余弦函数的拉普拉斯变换:L[sin(at)] = a/(s^2+a^2)L[cos(at)] = s/(s^2+a^2)3.7常见微分和积分公式的拉普拉斯变换:L[df(t)/dt] = sF(s) - f(0)L[∫[0,t]f(τ)dτ]=1/s×F(s)4.拉普拉斯反变换公式f(t) = L^(-1)[F(s)] = 1/(2πj) × ∫[-j∞,j∞] e^(st)F(s) ds5.拉普拉斯变换的性质5.1线性性:L[af(t) + bg(t)] = aF(s) + bG(s),其中a、b为常数5.2微分性:L[df(t)/dt] = sF(s) - f(0)5.3积分性:L[∫[0,t]f(τ)dτ]=1/s×F(s)5.4积分定理:∫[0,∞) f(t) dt = F(0+)5.5初值定理:lim(s→∞) sF(s) = f(0+)5.6终值定理:lim(t→0+) f(t) = lim(s→0) sF(s)6.拉普拉斯变换在信号处理中的应用拉普拉斯变换在信号处理领域有广泛的应用。
拉普拉斯变换微分定理三阶推导拉普拉斯变换微分定理是微分和拉普拉斯变换之间的一个重要关系。
它可以帮助我们将微分方程转换为代数方程,从而简化问题的求解。
在本文中,我将深入探讨拉普拉斯变换微分定理的三阶推导,并分享我的观点和理解。
让我们回顾一下拉普拉斯变换的基本定义和性质。
拉普拉斯变换是一种将一个函数从时间域转换到复频率域的方法。
对于一个函数f(t)在t≥0的定义域上,它的拉普拉斯变换可以表示为:F(s) = L[f(t)] = ∫ (0 to ∞) e^(-st) f(t) dt其中,s是一个复变量,被称为拉普拉斯变换域中的复频率。
函数F(s)是f(t)的拉普拉斯变换。
接下来,让我们来推导拉普拉斯变换微分定理的三阶形式。
我们从拉普拉斯变换的基本定义开始:L[f'(t)] = sF(s) - f(0)这是拉普拉斯变换微分定理的一阶形式。
它告诉我们,对于一个函数f(t)的导数f'(t),它的拉普拉斯变换等于s乘以f(t)的拉普拉斯变换减去f(t)在t=0时刻的值。
现在,让我们将这个一阶形式应用到函数的二阶导数上。
假设我们有一个函数f(t),它的二阶导数表示为f''(t)。
我们可以首先求出f'(t)的拉普拉斯变换,然后再对结果应用一阶形式的拉普拉斯变换微分定理。
根据一阶形式的定理,f'(t)的拉普拉斯变换为:L[f''(t)] = sF'(s) - f'(0)现在,让我们对这个结果应用一阶形式的拉普拉斯变换微分定理。
我们需要求出F'(s)的拉普拉斯变换,然后再对结果应用一阶形式的定理。
我们可以使用一阶形式的定理来计算F(s)的导数:F'(s) = L[f'(t)] = sF(s) - f(0)将这个结果代入到L[f''(t)]的表达式中,我们得到:L[f''(t)] = [s(sF(s) - f(0))] - f'(0)进一步整理,我们可以得到拉普拉斯变换微分定理的二阶形式:L[f''(t)] = s^2F(s) - sf(0) - f'(0)现在,我们已经推导出了拉普拉斯变换微分定理的二阶形式。
拉普拉斯变换微分定理三阶(最新版)目录1.拉普拉斯变换的定义与性质2.微分定理的概念与应用3.三阶拉普拉斯变换微分定理的求解方法4.总结与展望正文一、拉普拉斯变换的定义与性质拉普拉斯变换是一种数学工具,用于将一个函数从一个域(如时域)转换到另一个域(如频域)。
拉普拉斯变换的基本公式为:L{f(t)} = F(s) = ∫[e^(-st) * f(t)]dt,其中 s 为复变量,t 为自变量。
拉普拉斯变换具有以下性质:1.时域的线性变换:如果 f(t) 和 g(t) 是时域的函数,那么 L{f(t) + g(t)} = L{f(t)} + L{g(t)}。
2.时域的微分:如果 f(t) 是时域的函数,那么 L{f"(t)} = s * F(s) - f(0)。
3.时域的积分:如果 f(t) 是时域的函数,那么 L{∫f(τ)dτ} = F(s) / s。
二、微分定理的概念与应用微分定理是拉普拉斯变换中的一个重要定理,它表示拉普拉斯变换和微分运算之间的关系。
微分定理的公式为:L{f"(t)} = s * F(s) - f(0)。
微分定理在求解微分方程、优化控制问题、信号处理等领域具有广泛的应用。
三、三阶拉普拉斯变换微分定理的求解方法对于三阶拉普拉斯变换微分定理,其求解方法较为复杂。
一般采用部分分式分解法,将三阶微分方程转化为一阶微分方程,然后通过求解一阶微分方程得到三阶微分方程的解。
四、总结与展望拉普拉斯变换微分定理是信号与系统、自动控制等领域的重要工具,对于解决实际问题具有重要意义。
三阶拉普拉斯变换微分定理作为其中的一种,其求解方法的研究有助于提高解决实际问题的能力。
拉普拉斯变换微分定理三阶拉普拉斯变换微分定理是拉普拉斯变换中的一个重要定理,它可以用来求解微分方程。
在本文中,我们将介绍拉普拉斯变换微分定理的三阶形式,并通过实例演示如何利用该定理解决实际问题。
拉普拉斯变换是一种将时域函数转换为复平面上的函数的数学工具。
它在信号处理、电路分析和控制系统等领域有着广泛的应用。
拉普拉斯变换微分定理是拉普拉斯变换的基本性质之一,它建立了时域函数与频域函数之间的关系。
我们来介绍拉普拉斯变换微分定理的三阶形式。
设函数f(t)和它的三阶导数f'''(t)在t=0时存在有限,且拉普拉斯变换F(s)存在。
那么,拉普拉斯变换微分定理的三阶形式可以表示为:s^3F(s) - s^2f(0) - sf'(0) - f''(0) = F'(s)其中,s是复平面上的变量,F(s)是f(t)的拉普拉斯变换,f'(t)表示f(t)的一阶导数。
下面我们通过一个实例来演示拉普拉斯变换微分定理的应用。
假设有一个电路,其中的电流i(t)满足以下微分方程:L(di(t)/dt) + Ri(t) = V(t)其中,L和R分别是电感和电阻的值,V(t)是输入电压。
要求求解这个微分方程,我们可以使用拉普拉斯变换微分定理。
对方程两边进行拉普拉斯变换,得到:L(sI(s) - i(0)) + RI(s) = V(s)其中,I(s)和V(s)分别是i(t)和V(t)的拉普拉斯变换,i(0)是i(t)在t=0时的初值。
根据拉普拉斯变换微分定理的三阶形式,我们可以得到:s^3I(s) - s^2i(0) - sI(s) - i(0) + R(sI(s) - i(0)) = V(s)整理上述方程,可以得到I(s)的表达式:I(s) = (V(s) + i(0)(s^2 + s + R))/(Ls^3 + Rs + L)通过对上述方程进行反变换,我们可以得到i(t)的表达式。