五年级几何奥数题

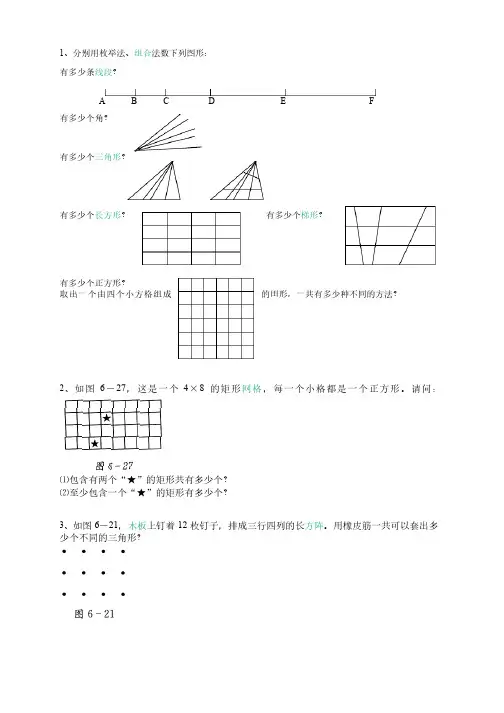
A B C D 1、分别用枚举法、、分别用枚举法、组合组合法数下列图形：法数下列图形：有多少条有多少条线段线段？E F 有多少个角？有多少个角？有多少个有多少个三角形三角形？有多少个有多少个长方形长方形？ 有多少个有多少个梯形梯形？有多少个正方形？有多少个正方形？取出一个由四个小方格组成的田形，一共有多少种不同的方法？的田形，一共有多少种不同的方法？2、如图6－27，这是一个4×8的矩形的矩形网格网格，每一个小格都是一个正方形。

请问：⑴包含有两个“★”的矩形共有多少个？⑴包含有两个“★”的矩形共有多少个？⑵至少包含一个“★”的矩形有多少个？⑵至少包含一个“★”的矩形有多少个？3、如图6－21，木板上钉着12枚钉子，排成三行四列的长枚钉子，排成三行四列的长方阵方阵。

用橡皮筋一共可以套出多少个不同的三角形？少个不同的三角形？4、如图，如图，在在半圆弧及其直径上共有9个点，个点，以这些点以这些点为顶点可以画出多少个为顶点可以画出多少个四边形四边形？多少个多少个三角形三角形？5、一个三角形的3条边上共有7个点，画出这7个点之间的全部连线（同一条边上的（同一条边上的两点两点不画）后，发现在这些连线的发现在这些连线的交点交点没有出现过重合；没有出现过重合；请问三角形内共有多少个交请问三角形内共有多少个交点？点？答案：答案： 1、C 2 6=15；C 2 5=10；C 2 5=10；30；C 2 5·C 25=100；60；25 2、30；162 3、C 3 12-20=200 4、C 4 9-1-C 3 4·C 1 5=105 5、C 4 7-4=27 。

例1
：下图是一座房屋的平面图，求这座房屋平面图的周长。

1、有一块纸板形状如图（单位：厘米），这块纸板的周长是多少厘米
例2：用同样大小的小正方形瓷砖铺一个正方形的卧室地面。

已知两条卧室地面的对角线铺黑色瓷砖，其他地方铺白色的，如果铺满整个地面要用47块黑色瓷砖，那么卧室中的白色瓷砖有多少块
例3：有一块长方形广场，沿着它不同的两条边各划出2米准备种树，剩下的部分仍是长方形，且周长为280米。

问：种树的面积是多少平方米
2、一块长方形木板，把长和宽各锯去6厘米，锯掉的面积为396平方厘米。

现在这块木板的周长是多少厘米
例4：一块花圃如图所示，梯形ABCD中有个直角三角形，AD=10米，BC=14米，AE=6米，DE=8米。

阴影部分的面积是多少平方米
3、图中三角形AED的面积是28平方厘米，长方形ABCD中，AD=7
第四讲
第五讲
厘米，CF=3厘米。

求梯形ABCF的面积。

4、在一个长方形花园中有个走道（图中的阴影部分），长方形的面积是216平方米，长18米，走道的宽米，走道的面积是多少平方米
5、图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

6、在下图中，AD=8厘米，BC=12厘米，CD=10厘米，三角形BCF的面积比三角形AEF大50平方厘米，AE长多少厘米
7、如图，正方形ABCD的周长是32厘米，AE长10厘米，BO长多少厘米。

五年级奥数典型练习100例（详细解析）1 五年级奥数(几何问题)及答案：直角三角形【答案解析】2 五年级奥数(几何问题)及答案：三角形面积右图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积.三角形面积答案：这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系.连接AD(见右上图)，可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等.因为三角形AGD是三角形ABD与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABG与三角形GCD面积仍然相等.根据等量代换，求三角形ABC的面积等于求三角形BCD 的面积，等于4×4÷2=83 五年级奥数(几何问题)及答案：阴影面积计算如图，长方形ABCD的面积是2平方厘米，EC=2DE，F是DG的中点.阴影部分的面积是多少平方厘米?【答案解析】如下图，连接FC，△DBF、△BFG的面积相等，设为x平方厘米;△FGC、△DFC的面积相等，设为y平方厘米，那么△DEF的面积为y平方厘米比较②、①式，②式左边比①式左边多2x，②式右边比①式右边大0.5，有2x=0.5，即x=0.25,y=0.25.而阴影部分面积为y+ y= ×0.25= 平方厘米.4 五年级奥数(几何面积)及答案：梯形阴影面积图中ABCD是梯形，三角形ADE面积是1.8，三角形ABF的面积是9,三角形BCF的面积是27.那么阴影部分面积是多少?【答案解析】设△ADF的面积为上，△BCF的面积为下，△ABF的面积为左，△DCF的面积为右.左=右=9;上×下=左×右=9×9=81，而下=27，所以上=81÷27=3.△ADE的面积为1.8，那么△AEF的面积为1.2，则EF：DF= ：=1.2：3=0.4.△CEF与△CDF的面积比也为EF与DF的比，所以有=0.4× =0.4×(3+9)=4.8.即阴影部分面积为4.8.5 五年级奥数(行程问题)及答案：外出时间某人下午六时多外出买东西，出门时看手表，发现表的时针和分针的夹角为1100，七时前回家时又看手表，发现时针和分针的夹角仍是1100.那么此人外出多少分钟?【答案解析】如下示意图，开始分针在时针左边1100位置，后来追至时针右边1100位置.6 五年级奥数(行程问题)及答案：发车间隔某人沿电车线路行走，每12分钟有一辆电车从后面追上，每4分钟有一辆电车迎面开来.假设两个起点站的发车间隔是相同的，求这个发车间隔.【答案解析】设电车的速度为a，行人的速度为b，因为每辆电车之间的距离为定值，设为l.7 五年级奥数(约数与倍数)及答案：最大公约数A,B两数都仅含有质因数3和5,它们的最大公约数是75.已知数A有12个约数，数B有10个约数，那么A,B两数的和等于多少?【答案解析】由题意知A可以写成3×52×a，B可以写成3×52×6,其中a、b为整数且只含质因子3、5.即A:31+x×52+y,B=31+m×52+n,其中x、Y、m、n均为自然数(可以为0)由A有12个约数,所以[(1+x)+1]×[ (2+y)+1]=(2+x)×(3+y)=12，所以 .对应A为31+2×52=675,31+1×52+1=1125,或31+0×52+4=46875;由B有10个约数,所以[(1+m)+1]×[(2+n)+l]=(2+m)×(3+n):10,所以 .对应B为31+0×52+2=1875.只有(675,1875)=75,所以A=675,B=1875.那么A,B两数的和为675+1875=25508 五年级奥数(包含与排除)及答案：读故事书甲、乙、丙都在读同-一本故事书，书中有100个故事.每个人都从某一个故事开始，按顺序往后读.已知甲读了7.5个故事，乙读了60个故事，丙读了52个故事.那么甲、乙、丙3人共同读过的故事最少有多少个?【答案解析】只考虑甲乙两人情况，有甲、乙都读过的最少为：75+60-100=35个，此时甲单独读过的为75-35=40个，乙单独读过的为60-35=25个;欲使甲、乙、丙三人都读过的书最少时，应将丙读过的书尽量分散在某端，于是三者都读过书最少为52-40=12个.9 五年级奥数(包含与排除)及答案：剪绳子有一根长为180厘米的绳子，从一端开始每隔3厘米作一记号，每隔4厘米也作一记号，然后将标有记号的地方剪断.问绳子共被剪成了多少段?【答案解析】只需先计算剪了多少刀，再加上1即为剪成的段数.从一端开始，将绳上距离这个端点整数厘米数的点编号，并将距离长度作为编号.10 五年级奥数(整除问题)及答案：除数各数位数字是0、1或2，且能被除数25整除的最小自然数是多少?【答案解析】225=25×9，所以要求分别能被25和9整除，要能被25整除，所以最后两位就是00。

小学奥数几何题100道及答案(完整版)题目1：一个正方形的边长是5 厘米，它的面积是多少平方厘米？解题方法：正方形面积= 边长×边长，即5×5 = 25（平方厘米）答案：25 平方厘米题目2：一个长方形的长是8 分米，宽是6 分米，它的周长是多少分米？解题方法：长方形周长= （长+ 宽）×2，即（8 + 6）×2 = 28（分米）答案：28 分米题目3：一个三角形的底是10 厘米，高是6 厘米，它的面积是多少平方厘米？解题方法：三角形面积= 底×高÷2，即10×6÷2 = 30（平方厘米）答案：30 平方厘米题目4：一个平行四边形的底是12 米，高是8 米，它的面积是多少平方米？解题方法：平行四边形面积= 底×高，即12×8 = 96（平方米）答案：96 平方米题目5：一个梯形的上底是 4 厘米，下底是6 厘米，高是5 厘米，它的面积是多少平方厘米？解题方法：梯形面积= （上底+ 下底）×高÷2，即（4 + 6）×5÷2 = 25（平方厘米）答案：25 平方厘米题目6：一个圆的半径是3 厘米，它的面积是多少平方厘米？解题方法：圆的面积= π×半径²，即3.14×3²= 28.26（平方厘米）答案：28.26 平方厘米题目7：一个半圆的半径是 4 分米，它的周长是多少分米？解题方法：半圆的周长= 圆周长的一半+ 直径，即3.14×4×2÷2 + 4×2 = 20.56（分米）答案：20.56 分米题目8：一个长方体的长、宽、高分别是5 厘米、4 厘米、3 厘米，它的表面积是多少平方厘米？解题方法：长方体表面积= （长×宽+ 长×高+ 宽×高）×2，即（5×4 + 5×3 + 4×3）×2 = 94（平方厘米）答案：94 平方厘米题目9：一个正方体的棱长是6 分米，它的体积是多少立方分米？解题方法：正方体体积= 棱长³，即6³= 216（立方分米）答案：216 立方分米题目10：一个圆柱的底面半径是2 厘米，高是5 厘米，它的侧面积是多少平方厘米？解题方法：圆柱侧面积= 底面周长×高，底面周长= 2×3.14×2，即2×3.14×2×5 = 62.8（平方厘米）答案：62.8 平方厘米题目11：一个圆锥的底面半径是3 厘米，高是4 厘米，它的体积是多少立方厘米？解题方法：圆锥体积= 1/3×底面积×高，底面积= 3.14×3²，即1/3×3.14×3²×4 = 37.68（立方厘米）答案：37.68 立方厘米题目12：两个边长为4 厘米的正方形拼成一个长方形，长方形的长和宽分别是多少？面积是多少？解题方法：长方形的长为8 厘米，宽为4 厘米，面积= 8×4 = 32（平方厘米）答案：长8 厘米，宽4 厘米，面积32 平方厘米题目13：一个三角形的面积是18 平方厘米，底是6 厘米，高是多少厘米？解题方法：高= 面积×2÷底，即18×2÷6 = 6（厘米）答案：6 厘米题目14：一个平行四边形的面积是24 平方米，底是 4 米，高是多少米？解题方法：高= 面积÷底，即24÷4 = 6（米）答案：6 米题目15：一个梯形的面积是30 平方分米，上底是5 分米，下底是7 分米，高是多少分米？解题方法：高= 面积×2÷（上底+ 下底），即30×2÷（5 + 7）= 5（分米）答案：5 分米题目16：一个圆环，外圆半径是5 厘米，内圆半径是 3 厘米，圆环的面积是多少平方厘米？解题方法：圆环面积= 外圆面积-内圆面积，即 3.14×（5²- 3²）= 50.24（平方厘米）答案：50.24 平方厘米题目17：一个长方体的棱长总和是48 厘米，长、宽、高的比是3:2:1，长方体的体积是多少立方厘米？解题方法：一条长、宽、高的和为48÷4 = 12 厘米，长为6 厘米，宽为4 厘米，高为2 厘米，体积= 6×4×2 = 48（立方厘米）答案：48 立方厘米题目18：一个正方体的表面积是54 平方分米，它的一个面的面积是多少平方分米？解题方法：一个面的面积= 表面积÷6，即54÷6 = 9（平方分米）答案：9 平方分米题目19：一个圆柱的底面直径是4 分米，高是3 分米，它的表面积是多少平方分米？解题方法：底面积= 3.14×（4÷2）²= 12.56 平方分米，侧面积= 3.14×4×3 = 37.68 平方分米，表面积= 2×12.56 + 37.68 = 62.8（平方分米）答案：62.8 平方分米题目20：一个圆锥的底面周长是18.84 分米，高是5 分米，它的体积是多少立方分米？解题方法：底面半径= 18.84÷3.14÷2 = 3 分米，体积= 1/3×3.14×3²×5 = 47.1（立方分米）答案：47.1 立方分米题目21：一个长方体的水箱，长 5 分米，宽4 分米，高 3 分米，里面装满水，把水倒入一个棱长为5 分米的正方体水箱，水深多少分米？解题方法：水的体积= 5×4×3 = 60 立方分米，正方体水箱底面积= 5×5 = 25 平方分米，水深= 60÷25 = 2.4 分米答案：2.4 分米题目22：一块长方形的铁皮，长8 分米，宽6 分米，从四个角各切掉一个边长为1 分米的正方形，然后做成一个无盖的盒子，这个盒子的容积是多少立方分米？解题方法：盒子长6 分米，宽4 分米，高1 分米，容积= 6×4×1 = 24（立方分米）答案：24 立方分米题目23：一个圆柱的体积是60 立方厘米，底面积是12 平方厘米，高是多少厘米？解题方法：高= 体积÷底面积，即60÷12 = 5（厘米）答案：5 厘米题目24：一个圆锥和一个圆柱等底等高，圆柱的体积是27 立方分米，圆锥的体积是多少立方分米？解题方法：等底等高的圆锥体积是圆柱体积的1/3，即27×1/3 = 9（立方分米）答案：9 立方分米题目25：把一个棱长为 6 厘米的正方体铁块熔铸成一个底面积为36 平方厘米的圆柱体，这个圆柱体的高是多少厘米？解题方法：正方体体积= 6³= 216 立方厘米，圆柱体的高= 体积÷底面积，即216÷36 = 6（厘米）答案：6 厘米题目26：一个直角三角形的两条直角边分别是3 厘米和4 厘米，斜边是5 厘米，这个三角形的面积是多少平方厘米？解题方法：直角三角形面积= 两条直角边乘积的一半，即3×4÷2 = 6（平方厘米）答案：6 平方厘米题目27：一个等腰三角形的周长是20 厘米，其中一条腰长8 厘米，底边长多少厘米？解题方法：等腰三角形两腰相等，所以底边长= 周长-腰长×2，即20 - 8×2 = 4（厘米）答案：4 厘米题目28：一个扇形的圆心角是90°，半径是6 厘米，这个扇形的面积是多少平方厘米？解题方法：扇形面积= 圆心角÷360°×圆的面积，即90÷360×3.14×6²= 28.26（平方厘米）答案：28.26 平方厘米题目29：一个长方体的底面是边长为5 厘米的正方形，高是8 厘米，这个长方体的体积是多少立方厘米？解题方法：长方体体积= 底面积×高，底面积= 5×5 = 25 平方厘米，体积= 25×8 = 200（立方厘米）答案：200 立方厘米题目30：一个圆柱的底面周长是18.84 厘米，高是10 厘米，它的体积是多少立方厘米？解题方法：底面半径= 18.84÷3.14÷2 = 3 厘米，体积= 3.14×3²×10 = 282.6（立方厘米）答案：282.6 立方厘米题目31：一个圆锥的底面直径是8 厘米，高是6 厘米，它的体积是多少立方厘米？解题方法：底面半径= 8÷2 = 4 厘米，体积= 1/3×3.14×4²×6 = 100.48（立方厘米）答案：100.48 立方厘米题目32：把一个棱长为8 厘米的正方体木块削成一个最大的圆柱，这个圆柱的体积是多少立方厘米？解题方法：圆柱的底面直径和高都是8 厘米，体积= 3.14×（8÷2）²×8 = 401.92（立方厘米）答案：401.92 立方厘米题目33：一个长方体玻璃缸，从里面量长4 分米，宽 3 分米，高5 分米，缸内水深2.5 分米。

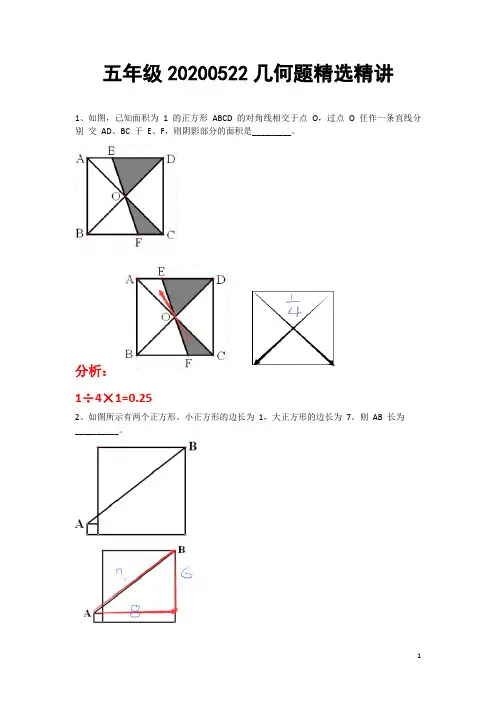
五年级20200522几何题精选精讲1、如图，已知面积为1 的正方形ABCD 的对角线相交于点O，过点O 任作一条直线分别交AD、BC 于E、F，则阴影部分的面积是_________。

分析：1÷4×1=0.252、如图所示有两个正方形。

小正方形的边长为1，大正方形的边长为7。

则AB 长为__________。

分析：一般求线段长度，可以考虑勾股定理。

7+1=8，7-1=6，AB ²=6²+8²=10²，所以AB=10 。

3、、如图所示，设F 为正方形ABCD 边AD 上一点，CE⊥CF 交AB 的延长线于E，若正方形ABCD 的面积为64，△CEF 的面积为50，则△CBE 的面积为__________。

方法一：分析：∠DCF+∠FCB=90°=∠FCB+∠BCE=90°，所以∠DCF=∠BCE，所以三角形DCF与三角形BCE是全等（完全一样的）。

BC²=64=8²，所以BC=8EC=FC，所以EC×CF÷2=EC×EC÷2=50，所以EC²=100，所以BE²=100-64=36=6²，所以BE=6，所以S△BEC=8×6÷2=24。

方法二：三个正方形，大中小，中正方形面积为50+50=100，所以EC²=100，因为BC²=64，所以BE²=100-64=36=6²，所以BE=6，所以大正方形边长为6+8=14，面积14²=196，所以阴影面积为：196-100=96、96÷4=24 。

4、如图，已知∠ MON= 40°，P 是∠MON 中的一定点，点A、B 分别在射线OM、ON 上移动，当△PAB 周长最小时，求∠APB 的度数。

分析：过P点作关于边OM的对称点D点，过P点作关于边ON的对称点C点，所以AP=AD，BP=BC，所以三角形ABP周长为DA+AB+BC 即点D与点C之间的长度，显然两点之间，直线段最短，所以线段DC与边OM和ON交于点A和B两点。

五年级经典奥数题及答案50道1. 在数轴上，AB、BC、CD、DE都是长度为1的线段，且它们依次相接，形成的五边形面积是多少？答案：22. 在一个长方形牛肚子里，画一条分割线将牛肚子分成两个小肚子，这条分割线的长度是8，面积相等的两个小肚子面积之和是多少？答案：483. 一个完整的圆披萨可以被等分成8个部分，每个底角为45度的扇形部分面积是多少？答案：1/8 π4. 在一个正方形BILL的内部，画一个面积等于BILL面积一半的正方形，这个正方形的边长是多少？答案：1/4 BILL的边长5. 一个半圆形的花坛直径是4米，花坛的花种在圆弧边上，两个相邻花之间的圆心角大小是45度，整个花坛可以有多少朵花？答案：86. 总和为111的两个正整数互质，这两个数中比较小的一个是多少？答案：377. 在一个长方形的表面上，剪去四个面积相等、四边形形状相同的小正方形，它们的边长分别是2，3，4和6，剩下的部分的面积是多少？答案：308. 在一个三角形ABC中，点D是AB边上的中点，点E是BC边上的中点，点F是CA边上的中点，连接点DEF，这个三角形被DEF分成了几个小三角形？答案：49. 一个正方形牌子上印有四个数字，每个数字都是2，3，4，5中的一个，每个数字只能用一次，求所有可能的四个数字组合方式。

答案：2410. 在一个三角形ABC中，角A是直角，BD是角B的平分线，E是AC上的一点，且角BDE和角BAC相等，求角ABC和角ACB的大小。

答案：45度11. 算式85×21×44×11的个位数字是多少？答案：012. 在一个正方形草坪的四个角上，分别立了四个灯柱，然后把草坪抬起，折成两个三角形，进行了运输。

运输过程中，两个三角形任意一个三角形都不能被折叠成平面，这个时候灯柱的相对位置改变了吗？答案：没有改变13. 一个正六面体每个面被划分成相同的10个小正方形，该六面体中有多少个顶点？答案：814. 给出一个两位数AB，其中A和B分别代表数字百位和个位，如果翻转后得到另一个两位数BA，且AB和BA的和是198，那么AB是多少？答案：9915. 求一个三位数ABC可以整除11的充要条件是什么？答案：A-B+C是11的倍数。

五年级20200522几何题精选精讲1、如图，已知面积为1 的正方形ABCD 的对角线相交于点O，过点O 任作一条直线分别交AD、BC 于E、F，则阴影部分的面积是_________。

分析：1÷4×1=0.252、如图所示有两个正方形。

小正方形的边长为1，大正方形的边长为7。

则AB 长为__________。

分析：一般求线段长度，可以考虑勾股定理。

7+1=8，7-1=6，AB ²=6²+8²=10²，所以AB=10 。

3、、如图所示，设F 为正方形ABCD 边AD 上一点，CE⊥CF 交AB 的延长线于E，若正方形ABCD 的面积为64，△CEF 的面积为50，则△CBE 的面积为__________。

方法一：分析：∠DCF+∠FCB=90°=∠FCB+∠BCE=90°，所以∠DCF=∠BCE，所以三角形DCF与三角形BCE是全等（完全一样的）。

BC²=64=8²，所以BC=8EC=FC，所以EC×CF÷2=EC×EC÷2=50，所以EC²=100，所以BE²=100-64=36=6²，所以BE=6，所以S△BEC=8×6÷2=24。

方法二：三个正方形，大中小，中正方形面积为50+50=100，所以EC²=100，因为BC²=64，所以BE²=100-64=36=6²，所以BE=6，所以大正方形边长为6+8=14，面积14²=196，所以阴影面积为：196-100=96、96÷4=24 。

4、如图，已知∠ MON= 40°，P 是∠MON 中的一定点，点A、B 分别在射线OM、ON 上移动，当△PAB 周长最小时，求∠APB 的度数。

分析：过P点作关于边OM的对称点D点，过P点作关于边ON的对称点C点，所以AP=AD，BP=BC，所以三角形ABP周长为DA+AB+BC 即点D与点C之间的长度，显然两点之间，直线段最短，所以线段DC与边OM和ON交于点A和B两点。

小学五年级奥数几何题1.小学五年级奥数几何题1.一个长方体的无盖水族箱, 长是6m, 宽是60cm, 高是1.5m。

这个水族箱占地面积有多大？需要多少平方米的玻璃？它的体积是多少？2.要砌一道长15m, 厚24cm, 高3m的砖墙。

如果每立方米用砖525块, 一共用砖多少块？3.花园小区为居民新安装了50个休息的凳子, 凳面的长、宽、高分别是100cm, 45cm,4.5cm。

凳腿的长、宽、高分别是45cm, 5cm, 35cm, 做这些凳子至少用了混凝土多少方？4、“六一”儿童节前, 全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m, 高2.7m, 厚6cm的奥运心愿墙。

这面墙一共用了多少块积木？5、学校运来7.6立方米的沙子, 铺在一个长5米、宽38米的沙坑里, 可以铺多厚？2.小学五年级奥数几何题1.一个长、宽、高分别为40cm、30cm、20cm的小纸箱, 在所有棱上粘上一圈胶带, 至少需要多长的胶带？2.为迎接“五一”劳动节, 要在俱乐部的四周装上彩灯（地面的四边不装）。

已知俱乐部的长90米, 宽55米, 高20米, 工人叔叔至少需要多长的彩灯线？3.小卖部要做一个长2.2m, 宽40cm, 高80cm的玻璃柜台, 现要在柜台各边都安上角铁, 这个柜台需要多少米角铁？4、一个长方体的饼干盒, 长10cm宽6cm, 高12cm。

如果围着它贴一圈商标纸（上、下面不贴）, 这张商标纸的面积至少要多少平方厘米？5、光华街口装了一个新的铁皮邮箱, 长50cm, 宽40cm, 高78cm。

做这个邮箱至少需要多少平方厘米的铁皮？3.小学五年级奥数几何题（1）有一个棱长是4厘米的正方体, 从它的一个顶点处挖去一个棱长是1厘米的正方体后, 剩下的物体的体积和表面积各是多少？（2）一个正方体和一个长方体拼成一个新的长方体, 拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。

1、在正方形ABCD中(如图所示)，E,F分别是所在边的中点，四边形AGCD的面积占正方形面积的几分之几？2、如图所示，直角梯形ABCD的上与高相等，正方形DEFH的边长等于6厘米，阴影部分的面积是________平方厘米。

3、如图，四边形ABCD是长方形，E、F分别是AB、DA的中点，G是BF和DE的交点，四边形BCDG的面积是40平方厘米，那么四边形ABCD的面积是________平方厘米。

4、将正面是红色，背面是白色的纸剪成一个直角三角形ABC(如下图所示)，盖在桌面上，然后折叠使A与C重合。

这是红色部分的面积为5.25平方分米，盖住桌面的面积比原来减少了9.375平方分米，BD＝4.8分米，折痕的长度是_____分米。

1、解:连接AC。

可以知道G是三角形ABC的3条中线的相交点，就是重心。

所以：S△ACG=S△ABG=S△BCG=1/3*S三角形ABC=1/6*S正方形ABCD。

S四边形AGCD=S△ACG+S△ACD=（1/2+1/6）S正方形ABCD=2/3*正方形ABCD 四边形AGCD的面积占正方形ABCD面积2/3。

2、3、解：设长方形ABCD面积为S。

因为F、E是AD和AB的中点，所以S△ABF=S△ADE=S/4连接AG，同样F、E是AD和AB的中点，所以S△BEG=S△AEG=S△AFG=S△DFG=S△ABF/3=S/12 S四边形BCDG=S-S△ABF-S△DFG=S - S/4- S/12=2 S/3 S=3 四边形BCDG/2=60平方厘米4、解：三角形ABC面积=9.375×2+5.25=24平方厘米AB=24×2÷4.8=10厘米假设折痕和AB交于点E，和AC交于点F ，AE=1/2×10=5厘米EF=9.375×2÷5=3.75。

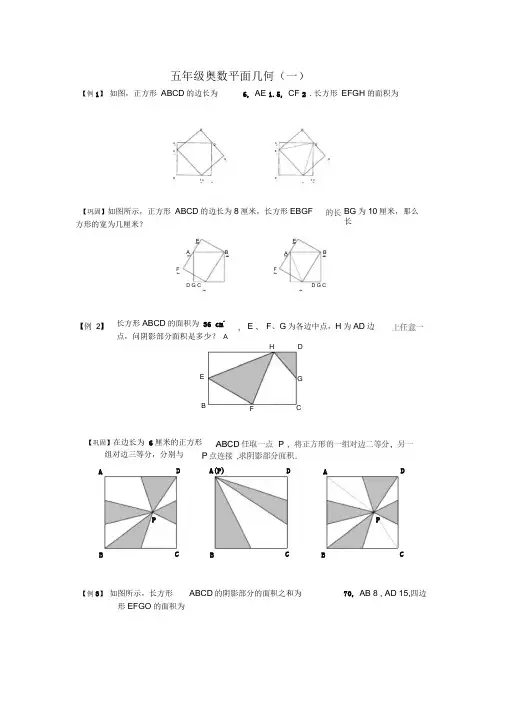
五年级奥数平面几何（一）【例1】 如图，正方形 ABCD 的边长为 6, AE 1.5, CF 2 .长方形 EFGH 的面积为GGBBA BBFFE HDEGB CF D A(P) DDA AP PA E A EBG 为10厘米，那么长【巩固】如图所示，正方形 ABCD 的边长为8厘米，长方形EBGF 方形的宽为几厘米？ 长方形ABCD 的面积为 36 cm 2点，问阴影部分面积是多少？ AF 、G 为各边中点，H 为AD 边F C F CD G CD G C【巩固】在边长为 6厘米的正方形 组对边三等分，分别与 C CCB B B【例3】 如图所示，长方形 形EFGO 的面积为ABCD 的阴影部分的面积之和为 70, AB 8 , AD 15,四边【巩固】【例4】【例5】【例6】如图，长方形ABCD的面积是36,的面积为E是AD的三等分点，AE 2ED ,则阴影部分已知ABC为等边三角形，面积为143,求阴影五边形的面积.乙、丙面积和为如图，已知CD左边部分面积是400 , D、E、F分别为三边的中点，已知甲、（丙是三角形HBC）5 , DE 7 , EF38,右边部分面积是15,65,FG 6,线段AB将图形分成两部分, 那么三角形ADG的面积是如图在△ ABC中，D,E分另U是AB,AC上的点，且AD: AB 2:5 , AE: AC 4:7 ,S A ADE 16平方厘米，求△ ABC的面积.【巩固】如图，三角形 ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形 ADE 的 面积等于1,那么三角形 ABC 的面积是多少？【巩固】如图，三角形ABC 被分成了甲（阴影部分）、乙两部分，BD DC 4 , BE 3 , AE 6, 乙部分面积是甲部分面积的几倍？行四边形ABCD 的面积是2 , 求平行四边形 ABCD 与四边形EFGH 的面积比.AAB C【例7】 如图在△ ABC 中，D 在BA 的延长线上,AE:EC 3:2 , S A ADE 12 平方厘米，求E 在AC 上，且 △ ABC 的面积.AB: AD 5:2,【例8】如图，平行四边形 ABCD, BE AB , CF2CB , GD 3DC , HA 4AD ,平如图所示， ABC 中，ABC 90 , AB 3 , BC 5,以AC 为一边向 ABC 外 作正方形ACDE ，中心为O,求 OBC 的面积.如图，以正方形的边 AB 为斜边在正方形作直角三角形ABE, AEB 90 , AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ，求三角形 OBE 的面积.【例9】如图所示的四边形的面积等于多少?【例10】【例11】 【例12】AB ED , AF CD , BC EF ，且有 AB 平行如下图，六边形 ABCDEF 中，于ED , AF 平行于CD , BC 平行于EF ,对角线FD 垂直于BD ,已知FD 24厘 米，BD 18厘米，请问六边形 ABCDEF 的面积是多少平方厘米?E E【例13】如图，三角形ABC 的面积是1 , E 是AC 的中点，点D 在BC 上，且BD :DC 1:2, AD 与BE 交于点F .则四边形 DFEC 的面积等于 .【例14】四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形 ABD 的面积等于三角形 BCD 的面积的1 ,且AO 2 , DO 3 ,那么CO 的长度是DO 的长3【巩固】如图，四边形被两条对角线分成 4个三角形，其中三个三角形的面积已知,求：⑴三角形 BGC 的面积；(2) AG:GC ?【例15】 如图，平行四边形 ABCD 的对角线交于 O 点，△ CEF 、△ OEF 、△ ODF 、△ BOE的面积依次是 2、4、4和6.求：⑴求 △ OCF 的面积；⑵求 △ GCE 的面积.【巩固】如图，长方形 ABCD 的面积是 分的面积是多少平方厘米 ？2平方厘米，EC 2DE , F 是DG 的中点.阴影部D EC【例16】如图，长方形ABCD中，BE:EC 2:3 , DF :FC 1:2 ,三角形DFG的面积为2平方厘米，求长方形ABCD【例17】如图，正方形ABCD面积为3平方厘米，M是AD边上的中点.求图中阴影部分的面积.【巩固】在下图的正方形ABCD中，E是BC边的中点，AE与BD相交于F点，三角形BEF 的面积为1平方厘米，那么正方形ABCD面积是平方厘米.【例18】已知ABCD是平行四边形，BC: CE 3:2，三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.【巩固】右图中 ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示 （单位：平方厘米），阴影部分的面积是 平方厘米.【巩固】右图中 ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示 （单位：平方厘米），阴影部分的面积是 平方厘米.知正方形DEFG 的面积48 , AK:KB 1:3，贝U BKD 的面积是多少?【例21】 下图中，四边形ABCD 都是边长为1的正方形，E 、F 、G 、H 分别是AB , BC ,【例19】如图，长方形 ABCD 被CE 、平方厘米，那么余下的四边形DF 分成四块，已知其中 3块的面积分别为 2、5、8 OFBC 的面积为 __________ 垩方厘米.【例20】如图，ABC 是等腰直角三角形,DEFG 是正方形，线段AB 与CD 相交于K 点.已CD, DA 的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m，那么，（m n ）的值等于 n则，△ ADE : §9边形DEGF【巩固】如图， DE 平行BC ，且AD 2 , AB 5 , AE 4，求AC 的长.△ ABC 中，DE , FG , MN , PQ , BC 互相平行,DF FM MP PB,贝U:岛边形DEGF : S 四边形FGNM : S 四边形MNQP : S 四边形PQCB【例22】如图，△ ABC 中,DE , FG , BC 互相平行,AD DF FB ,【巩固】如图，AD §△ ADE:&9边形FGCB【例23】如图，已知正方形 ABCD 的边长为4 , F 是BC 边的中点，E 是DC 边上的点,且DE :EC 1:3 , AF 与BE 相交于点G ,求S【例24】如图所示，已知平行四边形 ABCD 的面积是1 , E 、F 是AB 、AD 的中点，BF 交EC于M,求 BMG 的面积.△ABG。

五年级奥数题：几何与角度(A)题目一
已知图中的两个角角度之和为120度，求这两个角的度数。

解题思路：
设其中一个角的度数为x，则另一个角的度数为120 - x。

根据题目可知，这两个角的度数之和为120度，即x + (120 - x) = 120。

解方程，得到x = 60。

所以，这两个角的度数分别为60度和60度。

题目二
已知图中的角A的度数为30度，求角B的度数。

解题思路：
根据题目可知，角A的度数为30度，角A与角B为邻补角关系。

邻补角的度数之和为90度。

所以，角B的度数为90 - 30 = 60度。

题目三
已知图中的角度关系，求角度a的度数。

解题思路：
根据题目可知，角A的度数为130度，角a与角A为补角关系。

补角的度数之和为90度。

所以，角a的度数为90 - 130 = -40度。

注意：角度为负数表示角的顺时针方向旋转。

总结
本文档介绍了三道五年级奥数几何与角度题目的解题方法。

通过解题思路的分析和运算，可以准确得出每个角的度数。

希望对广大学生在学习几何与角度知识时有所帮助。

小学五年级长方形正方形的奥数题
长方形和正方形是小学数学中常见的几何形状。

在奥数题中，涉及到长方形和正方形的问题也很常见。

本文将为您提供一些小学五年级的奥数题，帮助学生熟悉和掌握解决这些问题的方法。

奥数题一
小明有一块长方形的纸，它的长是18厘米，宽是12厘米。

他想要将这块纸剪成正方形，且每个正方形的边长相等。

请问，他最多可以剪成几个正方形？每个正方形的边长是多少？
奥数题二
小华有一块正方形的纸，它的边长是15厘米。

他想要将这块纸剪成一些完全相同的小正方形拼成一个长方形，且所有小正方形的边长相等。

请问，这个长方形的长和宽各是多少个边长？
奥数题三
小红有一块长方形的纸，它的长是20厘米，宽是14厘米。

她想要将这块纸剪成一些完全相同的小正方形拼成一个正方形，且所有小正方形的边长相等。

请问，这个正方形的边长是多少厘米？
奥数题四
小李的教室是一个正方形，边长是10米。

他想要用一些长方形的瓷砖铺满整个教室的地板，且所有瓷砖的尺寸相同，且尽量不剪裁瓷砖。

请问，他需要多少块边长为2米的瓷砖？
以上是关于小学五年级长方形和正方形的奥数题。

希望通过解决这些问题，学生能够加深对长方形和正方形性质的理解，并提高解决几何问题的能力。

例1
1、有一块纸板形状如图（单位：厘米），这块纸板的周长是多少厘米？
例2：用同样大小的小正方形瓷砖铺一个正方形的卧室地面。

已知两条卧室地面的对角线铺黑色瓷砖，其他地方铺白色的，如果铺满整个地面要用47块黑色瓷砖，那么卧室中的白色瓷砖有多少块？
例3:有一块长方形广场，沿着它不同的两条边各划出2米准备种树,剩下的部分仍是长方形，且周长为280米。

问:种树的面积是多少平方米?
2、一块长方形木板,把长和宽各锯去6厘米,锯掉的面积为396平方厘米。

现在这块木板的周长是多少厘米？
例4:一块花圃如图所示，梯形ABCD 中有个直角三角形，AD=10米，BC=14米，AE=6米，DE=8米。

阴影部分的面积是多少平方米？
3、图中三角形AED ABCD 中，AD=7厘
米，CF=3厘米。

求梯形ABCF的面积。

4、在一个长方形花园中有个走道（图中的阴影部分）,长方形的面积是216平方米，长18米,走道的宽1。

2米，走道的面积是多少平方米?
5、图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

6、在下图中，AD=8厘米,BC=12厘米，CD=10厘米，三角形BCF的面积比三角形AEF大50平方厘米，AE长多少厘米？
7、如图，正方形ABCD的周长是32厘米，AE长10厘米，BO长多少厘米？。

五年级奥数(几何问题)题及答案-阴影面积计算
编者导语：小编特整理了五年级奥数(几何问题)每日一题及答案：阴影面积计算，几何方面只要找出规律，下一步解决思路就清晰明了了！
如图，长方形ABCD的面积是2平方厘米，EC=2DE，F是DG的中点.阴影部分的面积是多少平方厘米?
【答案解析】
如下图，连接FC，△DBF、△BFG的面积相等，设为x平方厘米;△FGC、△DFC的面积相等，设为y平方厘米，那么△DEF的面积为y平方厘米
比较②、①式，②式左边比①式左边多2x，②式右边比①式右边大0.5，有2x=0.5，即x=0.25,y=0.25.
而阴影部分面积为y+ y= ×0.25= 平方厘米.。

第12讲几何例1：如图所示阴影部分的面积是66平方厘米，则图中正方形的面积是平方厘米。

例2：如图所示，本行方形的长和宽分别是12厘米和9厘米，把三角形的三条边分别平均分成三段，得到A，B，C，D，E，F这了六个点，连接AF，BC，DE，DE得到一个六边形，这个六边形的面积。

例3：如图，三角形ABC的面积为30平方厘米，则梯形ABCD的面积是平方厘米。

例4：如图所示正八边形ABCDEFGH的面积为32平方厘米，M，N分别为AB，CD的重点。

则四边形MBNF的面积为平方厘米例5：如图所示，正方形ABCD的面积为54平方厘米，则阴影部分的面积为平方厘米。

例6：比较图中两个阴影部分I和II的面积，它们的大小关系是。

例7：如图所示，∠1=∠2，∠3=∠4，∠5=100度，那么∠A=_________度。

例8：如图所示，长方形ABCD 的长为25，宽为15。

四对平行线截长方形各边所得的线段的长已在图上标出，且横向的两组平行线都与BC 平行。

求阴影部分的面积。

2．平面几何中的计数问题例9：在等边三角形的三条边上分别取中点，并把分得的每一段再等分，如果继续下去，当每条边被八等分时，连接相对应的点，如图所示，可以组成_________个等边三角形。

例10：如图，有____________个正方形例11：图12-17是一个等边三角形花园，其中每一行都均匀地栽满了花。

已知图中一个小的等边三角形每条边上有15株花，这个花园共栽花_________株。

例12：如图所示，从豆豆家到学校，有4条纵路，3条横路。

如果豆豆上学时只能由上向下，从左到右，那么有_________种不同的走法。

3．平面几何知识的应用例13：如图所示，在一幅长为80厘米，宽为50厘米的矩形图画的四周镶一条宽为整数厘米的金色纸边（宽度保持不变），制成一幅面积为5400平方厘米的挂图，求金色纸边的宽度。

例14：小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料，生产一批形状如图所示的风筝，点E ，F ，G ，H 分别是四边形ABCD 各边的中点（即有EF=FG =21AC ，EH=FG=21BD ）。