第五节平面及其方程教案(最新整理)

平面及其方程说课稿人教版一、说课背景本次说课的内容选自人教版高中数学教材第五章“空间几何”，主要围绕平面及其方程的概念、性质和求解方法进行讲解。

本章节是空间解析几何的基础，对于培养学生的空间想象能力和逻辑推理能力具有重要意义。

二、教学目标1. 知识与技能目标：使学生理解平面的基本概念，掌握平面方程的推导过程及其应用。

2. 过程与方法目标：通过实例演示和练习，培养学生运用平面方程解决实际问题的能力。

3. 情感态度与价值观目标：激发学生对空间几何的兴趣，培养学生的探索精神和团队合作意识。

三、教学重点与难点1. 教学重点：平面的基本性质，平面方程的推导和应用。

2. 教学难点：平面方程的推导过程，以及如何利用平面方程解决实际问题。

四、教学方法与手段1. 教学方法：采用启发式教学法和探究式学习法，通过问题引导学生自主思考和探索。

2. 教学手段：运用多媒体课件展示平面图形，利用几何画板软件动态演示平面方程的推导过程。

五、教学过程1. 引入新课- 通过回顾上节课的立体几何知识，引出平面几何的概念。

- 通过实际问题（如：如何确定一个平面）激发学生的学习兴趣。

2. 概念讲解- 定义平面：平面是没有厚度的二维几何体，由无限多个点组成。

- 介绍平面的基本性质：平面内任意两点确定一条直线，平面与直线的关系等。

3. 平面方程的推导- 介绍平面方程的一般形式：Ax + By + Cz + D = 0。

- 通过实例演示如何从三个不在一条直线上的已知点推导出平面方程。

- 讲解法向量的概念及其在平面方程中的作用。

4. 平面方程的应用- 通过例题讲解如何求解平面与直线的交点问题。

- 探讨平面方程在实际生活中的应用，如建筑设计、工程测量等。

5. 课堂练习- 设计针对性练习题，让学生巩固平面方程的推导和应用。

- 分组讨论，鼓励学生相互合作，共同解决问题。

6. 课堂小结- 总结平面及其方程的主要内容。

- 强调平面方程在解决实际问题中的重要性。

平面的法式方程教案
教案名称：平面的法式方程教案
教学目标：
1. 理解平面的法式方程的概念和意义。

2. 掌握如何根据给定的条件，确定平面的法式方程。

3. 能够应用平面的法式方程解决实际问题。

教学重点和难点：
重点：平面的法式方程的概念和确定方法。

难点：如何根据给定的条件，确定平面的法式方程。

教学准备：
1. 教师准备：熟悉平面的法式方程的相关知识，准备案例和练习题。

2. 学生准备：复习平面几何的相关知识，准备参与课堂讨论和练习。

教学过程：
一、导入
教师通过引入平面的法式方程的概念，引发学生对该知识点的兴趣，激发学习积极性。

二、讲解
1. 介绍平面的法式方程的定义和基本形式。

2. 分步讲解如何根据给定条件，确定平面的法式方程。

3. 举例说明平面的法式方程在实际问题中的应用。

三、练习
教师布置练习题，让学生在课堂上或课后进行练习，巩固所学知识。

四、讨论
教师组织学生进行讨论，解答他们在学习过程中遇到的问题，加深对平面的法式方程的理解。

五、拓展
教师展示平面的法式方程在几何问题中的拓展应用，激发学生的思维，引导他们进行更深入的探讨。

六、总结
教师对本节课的内容进行总结，并强调重点和难点，引导学生进行复习。

教学反思：
教师在教学过程中要根据学生的实际情况，灵活调整教学方法，引导学生主动参与，提高学生的学习兴趣和能力。

同时，要及时总结教学反思，不断完善教学内容和方法。

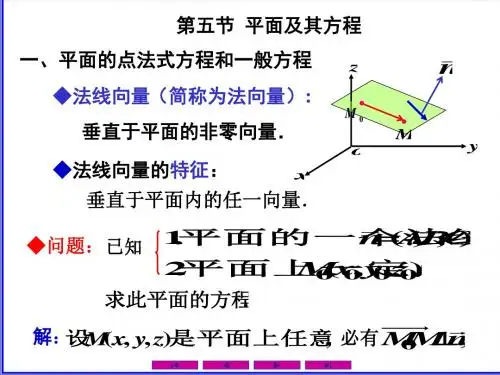
重庆科创职业学院授课教案课名：高等数学（上）教研窒：高等数学教研室班级：编写时间：解：设平面为，由平面过原点知　0=+++D Cz By Ax 0=D 由平面过点知 ，)2,3,6(-0236=+-C B A {4,1,2}⊥- n 024=+-∴C B A C B A 32-==⇒所求平面方程为0322=-+z y x 三、两平面的夹角：定义：两平面法向量之间的夹角称为两平面的夹角。

设平面，0:11111=+++∏D z C y B x A 0:22222=+++∏D z C y B x A ， 按照两向量夹角余弦公式有：},,{1111C B A n = },,{2222C B A n = 222222212121212121||cos C B A C B A C C B B A A ++⋅++++=θ几个常用的结论设平面1和平面2的法向量依次为和},,{1111C B A =n },,{2222C B A =n 1) 两平面垂直：（法向量垂直）0212121=++C C B B A A 2) 两平面平行：（法向量平行）212121C C B B A A ==3) 平面外一点到平面的距离公式：设平面外的一点，平),,(0000z y x P 面的方程为 ，则点到平面的距离为0=+++D Cz By Ax 222000C B A DCz By Ax d +++++=例3：研究以下各组里两平面的位置关系：013,012)1(=-+=+-+-z y z y x 01224,012)2(=--+-=-+-z y x z y x 02224,012)3(=-++-=+--z y x z y x 旁批栏：解：(1)　，两平面相交，夹角60131)1(2)1(|311201|cos 22222=+⋅-++-⨯-⨯+⨯-=θ；601arccos=θ (2) ， ，两平面平}1,1,2{1-=n }2,2,4{2--=n 212142-=-=-⇒行．，所以两平面平行但不重合。

平面的方程与性质教案一、引言平面方程是数学中重要的概念之一，它描述了平面上的点与坐标之间的关系。

平面的方程可以用于解决直线与曲线的交点、考察平面上的几何性质等问题。

本教案将介绍平面的方程及其性质，从而帮助学生更好地理解和应用平面方程的知识。

二、平面方程的定义平面方程是描述平面上所有点的数学表达式。

通常，一般形式的平面方程可以表示为Ax + By + Cz + D = 0，其中A、B、C和D为常数，且A、B和C不全为零。

三、平面方程的性质1. 点与平面的关系给定一个平面方程Ax + By + Cz + D = 0以及一个点P(x, y, z)，如果将点P的坐标代入方程，使得等式成立，则点P在平面上。

2. 平面的法向量平面方程中的系数A、B和C构成了平面的法向量N = (A, B, C)。

法向量垂直于平面，并且平面上的任意两个不重合的向量与法向量的点积为零。

3. 平面的倾斜角平面的倾斜角表示了平面与坐标轴或者其他平面之间的夹角。

通过计算平面法向量与坐标轴或者其他平面的夹角，可以求得平面的倾斜角。

4. 平面与坐标轴的交点可通过将某个坐标置零，然后化简平面方程，得到平面与坐标轴的交点。

例如，将z置零，可以求得平面与xy平面的交点。

四、平面的方程的应用1. 直线与平面的交点给定一个平面和直线方程，可以通过联立平面方程和直线方程，求得直线与平面的交点坐标。

2. 平面的平行和垂直关系两个平面平行，意味着它们的法向量是共线的；两个平面垂直，意味着它们的法向量的点积为零。

3. 平面与坐标轴的比较通过平面的方程，可以比较平面与坐标轴的相对位置。

当平面方程中仅有两个坐标分量时，可判断平面与某个坐标轴平行；当平面方程中有三个坐标分量时，可判断平面与坐标轴有交点或者平行。

五、案例分析以一个具体的案例来应用平面方程的知识。

考虑一个平面方程为2x + 3y - z + 1 = 0的平面。

根据该方程的系数，平面的法向量为N = (2, 3, -1)。