有关圆锥曲线的经典结论(稻谷书屋)

《圆锥曲线》知识要点及重要结论一、椭圆1 定义 平面内到两定点21,F F 的距离的和等于常数)2(221F F a a >的点P 的轨迹叫做椭圆.若212F F a =，点P 的轨迹是线段21F F .若2120F F a <<，点P 不存在.2 标准方程 )0(12222>>=+b a b y a x ，两焦点为)0,(),0,(21c F c F -.)0(12222>>=+b a bx a y ，两焦点为),0(),,0(21c F c F -.其中222c b a +=. 3 几何性质椭圆是轴对称图形，有两条对称轴. 椭圆是中心对称图形，对称中心是椭圆的中心. 椭圆的顶点有四个，长轴长为a 2，短轴长为b 2，椭圆的焦点在长轴上.若椭圆的标准方程为)0(12222>>=+b a b y a x ，则b y b a x a ≤≤-≤≤-,；若椭圆的标准方程为)0(12222>>=+b a bx a y ，则a y a b x b ≤≤-≤≤-,.二、双曲线1 定义 平面内到两定点21,F F 的距离之差的绝对值等于常数)20(221F F a a <<的点的轨迹叫做双曲线. 若212F F a =，点P 的轨迹是两条射线.若212F F a >，点P 不存在.2 标准方程 )0,0(12222>>=-b a b y a x ，两焦点为)0,(),0,(21c F c F -.)0,0(12222>>=-b a by a x ，两焦点为),0(),,0(21c F c F -.其中222b a c +=. 3 几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心. 双曲线的顶点有两个21,A A ，实轴长为a 2，虚轴长为b 2，双曲线的焦点在实轴上.若双曲线的标准方程为)0,0(12222>>=-b a b y a x ，则R y a x a x ∈≥-≤,或；若双曲线的标准方程为)0,0(12222>>=-b a bx a y ，则R x a y a y ∈≥-≤,或.4 渐近线双曲线)0,0(12222>>=-b a b y a x 有两条渐近线x a b y =和x a by -=.即02222=-b y a x双曲线)0,0(12222>>=-b a b x a y 有两条渐近线x b a y =和x bay -=.即02222=-b x a y双曲线的渐进线是它的重要几何特征，每一双曲线都对应确定双曲线的渐进线，但对于同一组渐进线却对应无数条双曲线.与双曲线)0,0(12222>>=-b a b y a x 共渐进线的双曲线可表示为)0(2222≠=-λλby a x .直线与双曲线有两个交点的条件，一定要“消元后的方程的二次项系数0≠”和“0>∆”同时成立.5 等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线.等轴双曲线的标准方程为)0(12222>=-a a y a x 或)0(12222>=-a ax a y .等轴双曲线的渐近线方程为x y ±=.6 共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线.如：)0,0(12222>>=-b a b y a x 的共轭双曲线为)0,0(12222>>=-b a ax b y ，它们的焦点到原点的距离相等，因而在以原点为圆心，22b a +为半径的圆上.且它们的渐近线都是x a b y =和x ab y -=. 三、抛物线1 定义 平面内与一个定点F 和一条定直线F l (不在l 上) 的距离相等的点的轨迹叫做抛物线. 定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线.2 标准方程(1) )0(22>=p px y ，焦点为)0,2(p ，准线方程为2px -=，抛物线张口向右.(2) )0(22>-=p px y ，焦点为)0,2(p -，准线方程为2p x =，抛物线张口向左.(3) )0(22>=p py x ，焦点为)2,0(p ，准线方程为2p y -=，抛物线张口向上.(4) )0(22>-=p py x ，焦点为)2,0(p -，准线方程为2p y =，抛物线张口向下.其中p 表示焦点到准线的距离.3 几何性质抛物线是轴对称图形，有一条对称轴.若方程为)0(22>=p px y 或)0(22>-=p px y ，则对称轴是x 轴，若方程为)0(22>=p py x 或)0(22>-=p py x ，则对称轴是y 轴. 若抛物线方程为)0(22>=p px y ，则R y x ∈≥,0. 若抛物线方程为)0(22>-=p px y ，则R y x ∈≤,0. 若抛物线方程为)0(22>=p py x ，则R x y ∈≥,0. 若抛物线方程为)0(22>-=p py x ，则R x y ∈≤,0.圆锥曲线的一些重要结论【几个重要结论】1 已知椭圆)0(12222>>=+b a by a x 的两焦点为)0,(),0,(21c F c F -，),(00y x P 为椭圆上一点，则)1()()(2222020201ax b c x y c x PF -++=++=a a cx a a cx a cx ax c +=+=++=020202202)(2 因为a x a ≤≤-0，c a a acxc a c a cx c +≤+≤-<≤≤-000,， 所以a a cx PF +=01. 同理，acxa PF a PF 0122-=-=. 已知双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为)0,(),0,(21c F c F -，),(00y x P 为双曲线上一点，则a a cx PF +=01，a acxPF -=02. 2 椭圆)0(12222>>=+b a b y a x 的两焦点为21,F F ，P 为椭圆上一点，若θ=∠21PF F ，则21PF F ∆的面积为2tan cos 1sin 22αααb b =+. 解：根据椭圆的定义可得a PF PF 221=+ ① 由余弦定理可得αcos 242122212212PF PF PF PF F F c -+== ②由①②得)cos 1(2442122α+=-PF PF c a .从而αcos 12221+=b PF PF 所以，21F PF ∆的面积为2tan cos 1sin sin 212221ααααb b PF PF =+=双曲线)0,0(12222>>=-b a b y a x 的两焦点为21,F F ，P 为其上一点，若α=∠21PF F ，则21PF F ∆的面积为2cot cos 1sin sin 212221ααααb b PF PF =-=. 3 已知椭圆)0(1:2222>>=+b a by a x C ，N M ,是C 上关于原点对称的两点，点P 是椭圆上任意一点，当直线PN PM ,的斜率都存在，并记为PN PM k k ,时，那么PM k 与PN k 之积是与点P 位置无关的定值.解：设),(),,(1100y x M y x P ，则),(11y x N --.01010101,x x y y k x x y y k PN PM----=--=，从而2120212001010101x x y y x x y y x x y y k k PN PM --=----⋅--=⋅. 又因为),(),,(1100y x M y x P 都在椭圆上，故1,1221221220220=+=+by a x b y a x .两式相减得，022********=-+-b y y a x x ，因而2221202120ab x x y y -=--即22a b k k PN PM -=⋅.已知双曲线)0,0(12222>>=-b a by a x .N M ,是C 上关于原点对称的两点，点P 是双曲线上任意一点，当直线PN PM ,的斜率都存在，并记为PN PM k k ,时，那么PM k 与PN k 之积是与点P 位置无关的定值.【常用方法】1 在求轨迹方程时，若条件满足圆、椭圆、双曲线、抛物线的定义，则可以用定义求轨迹方程，这是常用求轨迹的数学方法，称为定义法.2本章经常会碰到直线l 与圆锥曲线C 相交于两点的问题，若已知l 过定点),(00y x P ，则可设l 的方程为0x x =或)(00x x k y y -=-.然后分两种情况进行研究，一般处理方法是把直线方程代入曲线C 的方程中，整理得到关于x 或y 的一元二次方程(要注意二次项系数是否为零).韦达定理和判别式经常要用到！若l 的条件不明显时，则可设l 的方程为m x =或m kx y +=.3 本章还经常用到“点差法”：设直线l 与圆锥曲线C 交于点),(),,(2211y x B y x A ,则B A ,两点坐标都满足曲线C 的方程，然后把这两个结构相同的式子相减，整理可以得到直线AB 的斜率1212x x y y --的表达式，也经常会出现2121,y y x x ++，这样又可以与线段AB 的中点),(00y x P 联系起来！4 若三点),(),,(),,(002211y x P y x B y x A 满足以线段AB 为直径的圆经过点P 或BP AP ⊥时，常用处理方法有：①根据勾股定理可得222PB PA AB +=；②根据AP 的斜率与BP 的斜率之积为1-，可得120201010-=--⋅--x x y y x x y y ； ③根据),(),,(,002020101y y x x PB y y x x PA PB PA --=--==⋅可得0))(())((02010201=--+--y y y y x x x x .5求轨迹方程的方法常见的有：直接法、定义法、待定系数法、代入法（也叫相关点法）.1 椭圆22221(0)x y a b a b +=>>的参数方程是sin y b θ⎧⎨=⎩.离心率c e a ==，△PF 1F 2中，记12F PF α∠=, 12PF F β∠=,12F F P γ∠=，则有sin sin sin ce aαβγ==+.线到中心的距离为2a c，焦点到对应准线的距离(焦准距)2b p c =。

圆锥曲线中的重要性质经典精讲上性质一：椭圆中焦点三角形的内切圆圆心轨迹是以原焦点为顶点的椭圆双曲线中焦点三角形的内切圆圆心轨迹是以过原顶点的两平行开线段(长为2b )1．动点P 在椭圆22143x y +=上，12,F F 为椭圆之左右焦点，点G 为△12F PF 内心，试求点G 的轨迹方程.2．动点P 在双曲线22143x y -=上，12,F F 为双曲线之左右焦点，圆G 是△12F PF 的内切圆，探究圆G 是否过定点，并证明之.性质二：圆锥曲线的焦点弦的两个焦半径倒数之和为定值。

椭圆的焦点弦的两个焦半径倒数之和为常数11112||||AF BF ep+= 双曲线的焦点弦的两个焦半径倒数之和为常数 AB 在同支时11112||||AF BF ep += AB 在异支时11112||||||AF BF ep-= 抛物线的焦点弦的两个焦半径倒数之和为常数112||||AF BF ep+=3.椭圆22143x y +=，F 为椭圆之左焦点，过点F 的直线交椭圆于A ，B 两点，是否存在 实常数λ，使AB FA FB λ=•恒成立.并由此求∣AB ∣的最小值.性质三：圆锥曲线相互垂直的焦点弦长倒数之和为常数椭圆互相垂直的焦点弦倒数之和为常数epe CD AB 22||1||12-=+ 双曲线互相垂直的焦点弦倒数之和为常数epe CD AB 2|2|||1||12-=+ 抛物线互相垂直的焦点弦倒数之和为常数epe CD AB 22||1||12-=+ 4． 椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线12,l l 分别交椭圆于A ，B 两点和C ，D 两点，且12l l ⊥，是否存在实常数λ，使AB CD AB CD λ+=•恒成立.并由此求四边形ABCD 面积的最小值.性质四：椭圆、双曲线、抛物线的焦点弦直线被曲线及对称轴所分比之和为定值5．椭圆22184x y +=，点1F 为椭圆之左焦点，过点1F 的直线1l 分别交椭圆于A ，B 两点，设直线AB 与y 轴于点M ，11,,MA AF MB BF λμ==试求λμ+的值.性质五：椭圆、双曲线的焦半径向量模的比之和为定值过椭圆或双曲线上任点A 作两焦点的焦点弦AB ，AC ，其共线向量比之和为定值．即定值=-+=+==222211112ee C F AF BF AF μλμλ6．方向向量为(1,3)e =的直线l 过点(0,A -和椭圆2222:1x y C a b+=(0)a b >>的焦点，且椭圆C 的中心O 和椭圆的右准线上的点B 满足：0,OB e AB AO •==.⑴求椭圆C 的方程；⑵设E 为椭圆C 上任一点，过焦点12,F F 的弦分别为,ES ET ,设111,EF FS λ=222EF F T λ=，求12λλ+的值.圆锥曲线中的重要性质经典精讲中性质一：过圆锥曲线焦点所在轴上任意一点N 〔t,0〕的一条弦端点与对应点⎪⎪⎭⎫⎝⎛0,2t a 的连线所成角被对称轴平分。

当 M (x0, y0 ) 在左支上时， | MF1 | ex0 a , | MF2 | ex0 a （同上）
9. 设过双曲线焦点 F 作直线与双曲线相交 P 、Q 两点， A 为双曲线长轴上一个顶点， 连结 AP 和 AQ 分别交相应于焦点 F 的双曲线准线于 M 、 N 两点，则 MF NF .（同上）
1（ a
0, b
0 ）的左右焦点分别为
F , F2 ，点 P 为双曲线上任意一点：
F1PF2
，则双曲线的焦点角形的面积为
S F1PF2
b2co t .（同上） 2
x2 y2 8. 双曲线 a2 b 2 1 （ a 0, b 0 ）的焦半径公式：
F1 ( c , 0 ) , F2 (c,0)
当 M (x0, y0 ) 在右支上时， | MF1 | ex0 a , | MF2 | ex0 a .
a2c2k 2 a2b2
xP xQ
， xP xQ
M
2 a 2k 2c
2b2 ck
2abkN
， yP yQ
， yP yQ
，
M
M
M
第 2 页，共 18 页
xP yQ xQ y P
2a 2b 2k ， xP yQ
M
xQ ቤተ መጻሕፍቲ ባይዱP
再根据上一条性质可得结论。
2 abckN ，则 x
M
2a2b2k 2a2bkN
M 2abckN
M 2 ab2 ck
a
M
M
a2
，
c
11. （点差法）
kOM k AB 即 K AB
AB 是椭圆
x2 a2
b2 a2 ，
b 2x0 a2 y0

圆锥曲线是一种常见的几何曲线，它是由一个固定的圆盘和一条永远经过圆盘中心的直线（称为锥轴）所构成的曲线。

圆锥曲线有许多有趣的性质，下面是一些关于圆锥曲线的结论：
1 圆锥曲线的经过点数是无限的，因此它是一条无端的曲线。

2 圆锥曲线是一条连续曲线，因此它不会断开。

3 圆锥曲线的经过点都在相同的平面内，因此它是一条二维曲线。

4 圆锥曲线的形状受到锥轴的方向和斜率的影响。

如果锥轴垂直于
圆盘，则圆锥曲线是一个圆；如果锥轴斜率较大，则圆锥曲线会变得较长和较细；如果锥轴斜率较小，则圆锥曲线会变得较短和较厚。

5 圆锥曲线是一条对称曲线，即对于任意一条垂直于锥轴的直线，
圆锥曲线的两侧都是对称的。

6 圆锥曲线的长度是无限的，因此它是一条无限长的曲线。

希望这些信息能帮到你！。

( ) F1F=2 2c c=2 a2 − b2
关于 x 轴、 y 轴、原点对称
离心率
e= c = a
1−
b2 a2
(0
<
e
< 1) e
越小，椭圆越圆；e
越大，椭圆越扁
( ) 结论
1.（1）、与椭圆
x2 a2
+
y2 b2
= 1共焦点的椭圆的方程可设为
a
x2 2+
λ
+
y2 = b2 + λ
1, b2 + λ > 0
.
x2 （2）、与椭圆 a2
+
y2 b2
= 1有相同的离心率的椭圆可设为
x a
2 2
+
y2 b2
= λ , bx22
+
y2= a2
λ,(λ > 0).
结论 2.椭圆的两焦点分别为 F1, F2 , P 是椭圆上任意一点,则有以下结论成立: （1）、第一定义： PF1 + PF2 = 2a ； （2）、焦半径的最大值与最小值： a − c ≤ PF1 ≤ a + c ；
一．有关椭圆的经典结论
焦点的位置
圆锥曲线的二级结论
焦点在 x 轴上
焦点在 y 轴上
图形
标准方程 范围
顶点
轴长 焦点 焦距 对称性
x2 + y2= a2 b2
1(a > b > 0)
y2 + x2= a2 b2
1(a > b > 0)
−a ≤ x ≤ a 且 −b ≤ y ≤ b
−b ≤ x ≤ b 且 −a ≤ y ≤ a

圆锥曲线的经典结论一、椭圆1.点 P 处的切线 PT平分△ PF1F2 在点 P 处的外角 . （椭圆的光学性质）2.PT 平分△ PF1F2 在点 P处的外角，则焦点在直线 PT 上的射影 H点的轨迹是以长轴为直径的圆，除去长轴的两个端点 . （中位线）3.以焦点弦 PQ为直径的圆必与对应准线相离 . 以焦点半径 PF1 为直径的圆必与以长轴为直径的圆内切 . （第二定义）4.若 P0 ( x0,y0 )x2y21x0 x y0 y1.（求在椭圆b2上，则过 P0的椭圆的切线方程是b2a2a2导）5.若 P0 ( x0,y0 )x2y21外，则过 Po 作椭圆的两条切线切点为P1、P2，则切点在椭圆b2a2弦 P1P2 的直线方程是x0x y0 y 1. （结合 4）a2b26.椭圆 x2y2 1 (a ＞ b ＞ 0) 的左右焦点分别为F1 ， F 2 ，点 P 为椭圆上任意一点a2b2F1 PF2，则椭圆的焦点角形的面积为S F1PF2b2 tan . （余弦定理 +面积公式 +2半角公式）7.x2y21（ a＞ b＞ 0）的焦半径公式：椭圆2 b2a|MF1| a ex0 , | MF2 | a ex0 (F1 ( c,0) , F2 (c,0) M ( x0 , y0 ) ). （第二定义）8.设过椭圆焦点F 作直线与椭圆相交P 、 Q两点， A 为椭圆长轴上一个顶点，连结AP 和AQ分别交相应于焦点 F 的椭圆准线于M、 N两点，则M F⊥ NF9. 过椭圆一个焦点F 的直线与椭圆交于两点P、Q, A1、 A2 为椭圆长轴上的顶点，A1P和A2Q交于点 M，A2P 和 A1Q交于点 N，则 MF⊥ NF. MN 其实就在准线上，下面证明他在准线上根据第 8 条，证毕10. AB 是椭圆x2 y21 的不平行于对称轴的弦， M(x0 , y0 ) 为 AB 的中点，则a2 b2k OM k ABb2a2 ，即K AB b2x0 。

圆锥曲线是平面上的一类曲线，其中最常见的包括椭圆、抛物线和双曲线。

这些曲线在数学、物理和工程领域中都有广泛的应用，有许多性质和结论与它们相关。

以下是关于圆锥曲线的一些结论：1. 椭圆：椭圆是一个闭合的曲线，其性质包括：- 所有点到两个焦点的距离之和是常数。

- 长轴和短轴是椭圆的两个主要轴。

- 椭圆可以是正圆或扁圆，取决于长轴和短轴的比例。

- 椭圆在焦点处有反射性质，光线从一个焦点反射到另一个焦点。

2. 抛物线：抛物线是一个开放的曲线，其性质包括：- 所有从焦点出发的光线都会反射到抛物线上的焦点。

- 抛物线具有对称性，焦点位于开口一侧。

- 抛物线用于天文望远镜和抛物面反射器等光学设备中。

3. 双曲线：双曲线也是一个开放的曲线，其性质包括：- 双曲线有两个焦点，光线从一个焦点反射后会经过另一个焦点。

- 双曲线有两个分支，分别向外延伸。

- 双曲线在电磁波和引力场中都有应用，如双曲线轨道。

4. 参数方程：圆锥曲线可以用参数方程来表示，这种方式使得可以描述各种不同形状和位置的圆锥曲线。

5. 极坐标方程：圆锥曲线也可以用极坐标方程来表示，这对于描述曲线与极坐标原点的关系非常有用。

6. 焦点和直径：焦点是圆锥曲线的一个重要性质，它决定了曲线的形状。

直径是曲线的两个焦点之间的距离。

7. 曲线的切线：切线是曲线上某一点的局部近似，它与曲线的斜率和曲线方程相关。

8. 曲线的面积：可以计算圆锥曲线下方的面积，这对于计算曲线下方的积分和应用非常有用。

这些是关于圆锥曲线的一些基本结论，具体的性质和结论会根据具体的圆锥曲线类型和应用领域而有所不同。

圆锥曲线在数学、物理、工程和其他领域中都有广泛的应用，是重要的数学概念之一。

高中圆锥曲线结论总结
高中圆锥曲线结论总结
一、圆锥曲线的标准方程
圆锥曲线的标准方程为：
$$frac{x^2}{a^2}+frac{y^2}{b^2}=1$$
其中，a与b分别是椭圆的两个半径，且ab，a与b是正实数。

二、圆锥曲线的性质
1. 圆锥曲线的概念
圆锥曲线是由两个椭圆及其余部分所构成的四边形的边界线，是圆锥曲线的概念。

2. 圆锥曲线的对称性
由于圆锥曲线是由两个椭圆所构成，因此它具有x轴对称性和y 轴对称性，即曲线的俩边彼此对称。

3. 圆锥曲线的四个焦点
圆锥曲线的四个焦点分别位于椭圆的两个长轴端点，称为四个焦点。

4. 圆锥曲线的两个长轴
圆锥曲线的两个长轴是两个椭圆的长轴，它们的长度分别是a和b，两轴相交处的位置是圆锥曲线的中心点。

5. 圆锥曲线的弧长
圆锥曲线的弧长为：
$$mathcal{L}=2aarcsinfrac{b}{a}$$
其中，a与b是椭圆的两个半径，且ab。

6. 圆锥曲线的曲率
圆锥曲线的曲率为：
$$K=frac{a}{b}$$
其中，a与b是椭圆的两个半径，且ab。

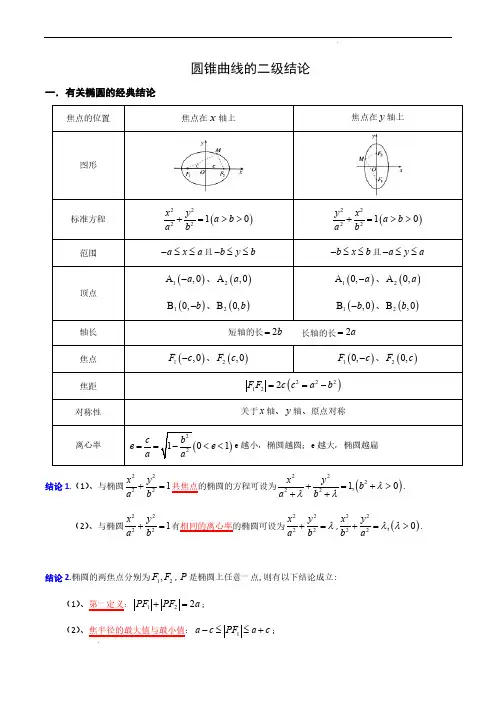
有关解析几何的经典结论一、椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b+=上，则过0P 的椭圆的切线方程是00221x x y y a b +=. 6. 若000(,)P x y 在椭圆22221x y a b+=外 ，则过Po 作椭圆的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y ya b+=. 7. 椭圆22221x y a b+= (a ＞b ＞0)的左右焦点分别为F 1，F 2，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点角形的面积为122tan 2F PF S b γ∆=.8. 椭圆22221x y a b+=（a ＞b ＞0）的焦半径公式：10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点，A 为椭圆长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点，则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点，A 1P 和A 2Q 交于点M ，A 2P 和A 1Q 交于点N ，则MF ⊥NF.11. AB 是椭圆22221x y a b+=的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则22OM AB b k k a ⋅=-，即0202y a x b K AB -=。

12. 若000(,)P x y 在椭圆22221x y a b+=内，则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+. 13. 若000(,)P x y 在椭圆22221x y a b+=内，则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b +=+. 二、双曲线1.点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2.PT 平分△PF 1F 2在点P 处的内角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3.以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.（内切：P 在右支；外切：P 在左支）5.若000(,)P x y 在双曲线22221x y a b-=（a ＞0,b ＞0）上，则过0P 的双曲线的切线方程是00221x x y y a b -=. 6.若000(,)P x y 在双曲线22221x y a b-=（a ＞0,b ＞0）外 ，则过Po 作双曲线的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y ya b -=. 7.双曲线22221x y a b-=（a ＞0,b ＞o ）的左右焦点分别为F 1，F 2，点P 为双曲线上任意一点12F PF γ∠=，则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8.双曲线22221x y a b-=（a ＞0,b ＞o ）的焦半径公式：(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时，10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时，10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点，A 为双曲线长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点，则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点，A 1P 和A 2Q 交于点M ，A 2P 和A 1Q 交于点N ，则MF ⊥NF.11.AB 是双曲线22221x y a b -=（a ＞0,b ＞0）的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则0202y a x b K K AB OM =⋅，即0202y a x b K AB=。

★说明:圆锥曲线我们并未学完，有些容（如焦半径公式），将此资料发到群里是想让大家在日常学习过程中自我感悟使用，不要过分纠结于此！有关解析几何的经典结论一、椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆切.5. 若000(,)P x y 在椭圆22221x y a b +=上，则过0P 的椭圆的切线方程是00221x x y ya b +=.6. 若000(,)P x y 在椭圆22221x y a b +=外 ，则过Po 作椭圆的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y ya b+=.7. 椭圆22221x ya b+= (a ＞b ＞0)的左右焦点分别为F 1，F 2，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=（a ＞b ＞0）的焦半径公式：10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点，A 为椭圆长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点，则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点，A 1P 和A 2Q交于点M ，A 2P 和A 1Q 交于点N ，则MF ⊥NF.11. AB 是椭圆22221x y a b +=的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则22OM AB b k k a ⋅=-，即0202y a x b K AB -=。

超全圆锥曲线结论总结结论1:过圆2222x y a +=上任意点P 作圆222x y a +=的两条切线,则两条切线垂直.结论2:过圆2222x y a b +=+上任意点P 作⿰木阴圆22221(0)x y a b a b+=>>的两条切线,则两条切线垂直.结论3:过圆2222(0)x y a b a b +=->>上任意点P 作双曲线22221x y a b-=的两条切线,则两条切线垂直.结论4:过圆222x y a +=上任意不同两点,A B 作圆的切线,如果切线垂直且相交于P ,则动点P 的轨迹为圆:2222x y a +=.结论5:过椭圆22221(0)x y a b a b+=>>上任意不同两点,A B 作椭圆的切线,如果切线垂直且相交于P ,则动点P 的轨迹为圆2222x y a b +=+.结论6:过双曲线22221(0)x y a b a b-=>>上任意不同两点,A B 作双曲线的切线,如果切线垂直.且相交于P ,则动点P 的轨迹为圆2222x y a b +=-.结论7：点()00,M x y 在椭圆22221(0)x y a b a b +=>>上,过点M 作椭圆的切线方程为00221x x y ya b+= 结论8:点()00,M x y 在椭圆22221 0x y a b a b+=>>（）外,过点M 作椭圆的两条切线,切点分别为 ,A B 则切点弦AB 的直线方程为00221x x y ya b+=. 结论8:(补充)点()00,M x y 在椭圆22221 0x y a b a b+=>>（）内,过点M 作椭圆的弦AB (不过椭圆中心),分别过,A B 作椭圆的切线,则两条切线的交点P 的轨迹方程为直线:00221x x y ya b+=. 结论9:点()00,M x y 在双曲线22221(0,0)x y a b a b -=>>上,过点M 作双曲线的切线方程为00221x x y ya b-= 结论10:点()00,M x y 在双曲线22221(0,0)x y a b a b-=>>外,过点M 作双曲线的两条切线,切点分别为,A B 则切点弦AB 的直线方程为00221x x y ya b-=. 结论10:（补充）点()00,M x y 在双曲线22221(0,0)x y a b a b-=>>内，过点M 作双曲线的弦AB (不过双曲线中心),分别过,A B 作双曲线的切线,则两条切线的交点P 的轨迹方程为直线:00221x x y ya b-= 结论11:点()00,M x y 在抛物线22(0)y px p =>上,过点M 作抛物线的切线方程为()00y y p x x =+.结论12:点()00,M x y 在抛物线22(0)y px p =>外，过点M 作抛物线的两条切线，切点分别为,A B 则切点弦AB 的直线方程为()00y y p x x =+.结论12:（补充）点()00,M x y 在抛物线22(0)y px p =>内，过点M 作抛物线的弦AB ,分别过,A B 作抛物线的切线，则两条切线的交点P 的轨迹方程为直线:()00y y p x x =+.结论13:点()00,M x y 在椭圆2222()()1x m y n a b--+=上,过点M 作椭圆的切线方程为()()0022()()1x m x m y n y n a b ----+=结论14:点()00,M x y 在双曲线2222()()1x m y n a b---=上,过点M 作双曲线的切线方程为()()0022()()1x m x m y n y n a b -----=结论15:点()00,M x y 在抛物线2()2()y n p x m -=-上,过点M 作抛物线的切线方程为()()00()2y n y n p x x m --=+-.结论16:点()00,M x y 在椭圆2222()()1x m y n a b--+=外,过点M 作椭圆的两条切线,切点分别为,A B 则切点弦AB 的直线方程为()()0022()()1x m x m y n y n a b ----+=.结论17:点()00,M x y 在双曲线2222()()1x m y n a b---=外,过点M 作双曲线的两条切线，切点分别为,A B ,则切点弦AB 的直线方程为()()0022()() 1.x m x m y n y n a b -----=结论18:点()00,M x y 在抛物线2()2()y n p x m -=-外,过点M 作抛物线的两条切线，切点分别为,A B 则切点弦AB 的直线方程为()()00()2y n y n p x x m --=+-.结论16:（补充）点()00,M x y 在椭圆2222()()1x m y n a b --+=内，过点M 作椭圆的弦AB （不过椭圆中心）,分别过,A B 作椭圆的切线,则两条切线的交点P 的轨迹方程为直线:()()0022()()1x m x m y n y n ab----+=.结论17:(补充)点()00,M x y 在双曲线2222()()1x m y n a b ---=内,过点M 作双曲线的弦AB (不过双曲线中心),分别过,A B 作双曲线的切线,则两条切线的交点P 的轨迹方程为直线:()()0022()()1x m x m y n y n a b -----=结论18:(补充)点()00,M x y 在抛物线2()2()y n p x m -=-内,过点M 作抛物线的弦AB ,分别过,A B 作抛物线的切线，则两条切线的交点P 的轨迹方程为直线:()()00()2y n y n p x x m --=+-.结论19:过椭圆准线上一点M 作椭圆的两条切线,切点分别为,A B ,则切点弦AB 的直线必过相应的焦点F ,且MF 垂直切点弦AB .结论20:过双曲线准线上一点M 作双曲线的两条切线,切点分别为,A B 则切点弦AB 的直线必过相应的焦点F ，且MF 垂直切点弦AB .结论21:过抛物线准线上一点M 作抛物线的两条切线,切点分别为,A B ,则切点弦AB 的直线必过焦点F ，且MF 垂直切点弦AB .结论22:AB 为椭圆的焦点弦，则过,A B 的切线的交点M 必在相应的准线上. 结论23:AB 为双曲线的焦点弦，则过,A B 的切线的交点M 必在相应的准线上. 结论24:AB 为抛物线的焦点弦，则过,A B 的切线的交点M 必在准线上.结论25:点M 是椭圆准线与长轴的交点,过点M 作椭圆的两条切线,切点分别为,A B ,则切点弦AB 就是通径.结论26:点M 是双曲线准线与实轴的交点,过点M 作双曲线的两条切线,切点分别为,A B ,则切点弦AB 就是通径.结论27:M 为抛物线的准线与其对称轴的交点,过点M 作抛物线的两条切线，切点分别为,A B ,则切点弦AB 就是其通径.结论28：过抛物线22(0)y px p =>的对称轴上任意一点(,0)(0)M m m ->作抛物线的两条切线，切点分别为,A B 则切点弦AB 所在的直线必过点(,0)N m .结论29:过椭圆22221(0,0)x y a b a b+=>>的对称轴上任意一点(,)M m n 作⿰木阴圆的两条切线,切点分别为,A B .(1)当0,||n m a =>时，则切点弦AB 所在的直线必过点2,0a P m ⎛⎫⎪⎝⎭; (2)当0,||m n b =>时，则切点弦AB 所在的直线必过点20,b Q n ⎛⎫⎪⎝⎭.结论30:过双曲线22221(0,0)x y a b a b-=>>的实轴上任意一点(,0)(||)M m m a <作双曲线（单支）的两条切线，切点分别为,A B ,则切点弦AB 所在的直线必过点2,0a P m ⎛⎫⎪⎝⎭. 结论31：过抛物线22(0)y px p =>外任意一点M 作抛物线的两条切线，切点分别为,A B ,弦AB 的中点为N ,则直线MN 必与其对称轴平行.结论32:若椭圆22221(0)x y a b a b +=>>与双曲线22221(0,0)x y m n m n-=>>共焦点,则在它们交点处的切线相互垂直.结论33:过椭圆外一定点P 作其一条割线,交点为,A B ,则满足||||||||AP BQ AQ BP ⋅=⋅的动点Q 的轨迹就是过P 作椭圆两条切线形成的切点弦所在的直线方程上.结论34:过双曲线外一定点P 作其一条割线,交点为,A B 则满足||||||||AP BQ AQ BP ⋅=⋅的动点Q 的轨迹就是过P 作双曲线两条切线形成的切点弦所在的直线方程上.结论35:过抛物线外一定点P 作其一条割线,交点为,A B 则满足||||||||AP BQ AQ BP ⋅=⋅的动点Q 的轨迹就是过P 作抛物线两条切线形成的切点弦所在的直线方程上.结论36:过双曲线外一点P 作其一条割线,交点为,A B ,过,A B 分别作双曲线的切线相交于点Q ,则动点Q 的轨迹就是过P 作双曲线两条切线形成的切点弦所在的直线方程上. 结论37:过椭圆外一点P 作其一条割线,交点为,A B 过,A B 分别作椭圆的切线相交于点Q ,则动点Q 的轨迹就是过P 作椭圆两条切线形成的切点弦所在的直线方程上.结论38:过抛物线外一点P 作其一条割线,交点为,A B ,过,A B 分别作抛物线的切线相交于点Q ,则动点Q 的轨迹就是过P 作抛物线两条切线形成的切点弦所在的直线方程上.结论39:从椭圆22221(0)x y a b a b +=>>的右焦点向椭圆的动切线引垂线,则垂足的轨迹为圆:222x y a +=.结论40:从双曲线22221(0,0)x y a b a b-=>>的右焦点向双曲线的动切线引垂线,则垂足的轨迹为圆:222x y a +=.结论41:F 是椭圆22221(0)x y a b a b +=>>的一个焦点,M 是椭圆上任意一点,则焦半径[,]MF a c a c ∈-+.结论42:F 是双曲线22221(0)x y a b a b-=>>的右焦点,M 是双曲线上任意一点.(1)当点M 在双曲线右支上,则焦半径MF c a ≥-;(2)当点M 在双曲线左支上,则焦半径MF c a ≥+.结论43:F 是抛物线22(0)y px p =>的焦点,M 是抛物线上任意一点,则焦半径022p p MF x =+≥. 结论44:椭圆上任一点M 处的法线平分过该点的两条焦半径的夹角（或者说M 处的切线平分过该点的两条焦半径的夹角的外角)，亦即椭圆的光学性质.结论45：双曲线上任一点M 处的切线平分过该点的两条焦半径的夹角（或者说M 处的法线平分过该点的两条焦半径的夹角的外角),亦即双曲线的光学性质.结论46:抛物线上任一点M 处的切线平分该点的焦半径与该点向准线所作的垂线的夹角,亦即抛物线的光学性质.结论47:椭圆的准线上任一点M 处的切点弦PQ 过其相应的焦点F ,且MF PQ ⊥. 结论48:双曲线的准线上任一点M 处的切点弦PQ 过其相应的焦点F ,且MF PQ ⊥. 结论49:抛物线的准线上任一点M 处的切点弦PQ 过其焦点F ,且MF PQ ⊥.结论50:椭圆上任一点P 处的切线交准线于,M P 与相应的焦点F 的连线交椭圆于Q ,则MQ 必与该椭圆相切,且MF PQ ⊥.结论51:双曲线上任一点P 处的切线交准线于,M P 与相应的焦点F 的连线交双曲线于Q ,则MQ 必与该双曲线相切，且MF PQ ⊥.结论52:抛物线上任一点P 处的切线交准线于,M P 与焦点F 的连线交抛物线于Q ,则MQ 必与该抛物线相切，且MF PQ ⊥.结论53:焦点在x 轴上的椭圆（或焦点在y 轴）上三点,,P Q M 的焦半径成等差数列的充要条件为,,P Q M 的横坐标(纵坐标)成等差数列.结论54:焦点在x 轴上的双曲线（或焦点在y 轴）上三点,,P Q M 的焦半径成等差数列的充要条件为,,P Q M 的横坐标（纵坐标）成等差数列.结论55:焦点在x 轴上的抛物线（或焦点在y 轴）上三点,,P Q M 的焦半径成等差数列的充要条件为,,P Q M 的横坐标（纵坐标）成等差数列.结论56:椭圆上一个焦点2F 关于椭圆上任一点P 处的切线的对称点为Q ,则直线PQ 必过该椭圆的另一个焦点1F .结论57:双曲线上一个焦点2F 关于双曲线上任一点P 处的切线的对称点为Q ,则直线PQ 必过该双曲线的另一个焦点1F .结论58:椭圆上任一点P (非顶点),过P 的切线和法线分别与短轴相交于£, ?Q S 则有,,P Q S 及两个焦点共于一圆上.结论59:双曲线上任一点P （非顶点)，过P 的切线和法线分别与短轴相交于,Q S ,则有,P Q ,S 及两个焦点共于一圆上.结论60:椭圆上任一点P (非顶点)处的切线与过长轴两个顶点,A A '的切线相交于,M M ',则必得到以MM '为直径的圆经过该椭圆的两个焦点.结论61:双曲线上任一点P (非顶点）处的切线与过实轴两个顶点,A A '的切线相交于,M M ',则必得到以MM '为直径的圆经过该双曲线的两个焦点.结论62:以椭圆的任一焦半径为直径的圆内切于以长轴为直径的圆. 结论63:以双曲线的任一焦半径为直径的圆外切于以实轴为直径的圆. 结论64:以抛物线的任一焦半径为直径的圆与非对称轴的轴相切.结论65：焦点在x 轴上的椭圆（或焦点在y 轴上）上任一点M （非短轴顶点）与短轴的两个顶点B ,B '的连线分别交x 轴（或y 轴）于,P Q ,则2P Q x x a =(或)2P Q y y a =.结论66:焦点在x 轴上的双曲线（或焦点在y 轴上）上任一点M (非顶点)与实轴的两个顶点,B B '的连线分别交y 轴（或x 轴）于,P Q ,则(2P Q y y b =-或)2P Q x x b =-.结论67:P 为焦点在x 轴上的椭圆上任一点（非长轴顶点),则12PF F ∆与边2PF (或1PF )相切的旁切圆与x 轴相切于右顶点A (或左顶点A ').结论68:P 为焦点在x 轴上的双曲线右支（或左支）上任一点,则12PF F ∆的内切圆与x 轴相切于右顶点A (或左顶点A ').结论69:AB 是过椭圆22221(0)x y a b a b+=>>的焦点F 的一条弦(非通径),弦AB 的中垂线交x 轴于N ,则||2||AB NF e=. 结论70:AB 是过双曲线22221(0,0)x y a b a b-=>>的焦点F 的一条弦（非通径,且为单支弦),弦AB 的中垂线交x 轴于M ,则||2||AB MF e=. 结论71:AB 是过抛物线22(0)y px p =>的焦点F 的一条弦（非通径),弦AB 的中垂线交x 轴于M ,则||2||AB MF =. 结论72:AB 为抛物线的焦点弦，分别过,A B 作抛物线的切线,则两条切线的交点P 在其准线上.结论73:AB 为椭圆的焦点弦,分别过,A B 作椭圆的切线,则两条切线的交点P 在其相应的准线上.结论74:AB 为双曲线的焦点弦,分别过,A B 作双曲线的切线，则两条切线的交点P 在其相应的准线上.结论75:AB 为过抛物线焦点F 的焦点弦，以AB 为直径的圆必与其准线相切.结论76:AB 为过椭圆焦点F 的焦点弦，以AB 为直径的圆必与其相应的准线相离（当然与另一条准线更相离）.结论77:AB 为过双曲线焦点F 的焦点弦，以AB 为直径的圆必与其相应的准线相交,截得的圆弧度数为定值,且为12arccos e. 结论78：以圆锥曲线的焦点弦AB 为直径作圆，若该圆与其相应的准线相切,则该曲线必为抛物线.结论79:以圆雉曲线的焦点弦AB 为直径作圆，若该圆与其相应的准线相离，则该曲线必为椭圆.结论80:以圆锥曲线的焦点弦AB 为直径作圆，若该圆与其相应的准线相交,则该曲线必为双曲线,此时截得的圆弧度数为定值,且为12arccose结论81:AB 为过抛物线22(0)y px p =>焦点F 的焦点弦,()()1122,,,A x y B x y ,则||AB =12x x p ++结论82:AB 为过椭圆22221(0)x y a b a b +=>>焦点F 的焦点弦,()()1122,,,A x y B x y ,则||AB 122a e x x =-+结论83:AB 为过双曲线22221(0,0)x y a b a b-=>>焦点F 的焦点弦,()()1122,,,A x y B x y .若AB 为单支弦，则12||2AB e x x a =+-;若AB 为双支弦，则|12|||2AB e x x a =++ 结论84:F 为抛物线的焦点,,A B 是抛物线上不同的两点,直线AB 交其准线l 于M ,则FM 平分AFB ∠的外角.结论85:F 为椭圆的一个焦点,,A B 是椭圆上不同的两点,直线AB 交其相应的准线l 于M ,则FM 平分AFB ∠的外角.结论86:F 为双曲线的一个焦点,,A B 是双曲线上不同的两点（同一支上),直线AB 交其相应的准线l 于M ,则FM 平分AFB ∠的外角.结论87:F 为双曲线的一个焦点,,A B 是双曲线上不同的两点（左右支各一点),直线AB 交其相应的准线l 于M ,则FM 平分AFB ∠.结论88:AB 是椭圆22221(0)x y a b a b+=>>过焦点F 的弦,点P 是椭圆上异于,A B 的任一点,直线PA PB 、分别交相应于焦点F 的准线l 于M N 、,则点M 与点N 的纵坐标之积为定值,且为42b c-.结论89:AB 是双曲线22221(0,0)x y a b a b-=>>过焦点F 的弦,点P 是双曲线上异于,A B任一点,直线PA 、PB 分别交相应于焦点F 的准线l 于M N 、,则点M 与点N 的纵坐标之积为定值,且为42b c-.结论90:AB 是抛物线22(0)y px p =>过焦点F 的弦，点P 是抛物线上异于,A B 的任一点,直线PA PB 、分别交准线l 于M N 、,则点M 与点N 的纵坐标之积为定值,且为2p -.结论91:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,P 为椭圆任一点（非长轴顶点),若直线PA PB 、分别交直线2(0)a x m a m=<<于M N 、,则M N y y ⋅为定值,且有()2222M N b m a y y m -⋅=结论92：,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EM FN ⋅为定值,且有()()222222a m a mb EM FN m -+-⋅=.结论93:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P 为椭圆上任一点（非长轴顶点)，若直线,AP BP 分别交直线2a x m=于M N 、,则EN FM ⋅为定值,且有()()222222a m a mb EN FM m -+-⋅=结论94:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P 为椭圆任一点（非长轴顶点)，若直线,AP BP 分别交直线2a x m=于M N 、,则FM FN ⋅为定值,且有()()222222am a m b FM FN m -+-⋅=结论95:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EM EN ⋅为定值,且有()()2222222a mb a m EM EN m +--⋅=结论96:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则BM FN ⋅为定值,且有()()22222a m a amb BM FN m -+-⋅=结论97:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P为椭圆任一点（非长轴顶点)，若直线,AP BP 分别交直线2a x m=于M N 、,则AM FN ⋅为定值,且有()()22222am a am b AM FN m ---⋅=结论98:,A B 为椭圆221(0)a b a b +=>>的长轴顶点,(,0),(,0),(0)E m F m m a -<<,P 为椭圆任一点（非长轴顶点)，若直线,AP BP 分别交直线2a x m=于M N 、,则AM BN ⋅为定值,且有()()22222a m ab AM BN m --⋅=结论99:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(0)E m F m m a -<<,P 为双曲线上任一点（非实轴顶点)，若直线,AP BP 分别交直线2a x m =于M N 、,则M N y y ⋅为定值,且有()2222M N b m a y y m -⋅=.结论100:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EM FN ⋅为定值,且有()()222222a m ab m EM FN m -++⋅=结论101:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EN FM ⋅为定值,且有()()222222a m ab m EN FM m -++⋅=结论102:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则FM FN ⋅为定值,且有()()222222am a b m FM FN m -+-⋅=结论103:,A B 为双曲线221(0,0)a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点（非实轴顶点，若直线,AP BP 分别交直线2a x m=于M N 、,则EM EN ⋅为定值，且有()()2222222a mb a m EM EN m ++-⋅=结论104:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则BM FN ⋅为定值,且有()()22222am a b amBM FN m -++⋅=结论105:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则AM FN ⋅为定值,且有()()22222a m ab amAM FN m -+-⋅=结论106:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),()E m F m m a ->,P 为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则AM BN ⋅为定值,且有()()22222a m ab AM BN m -+⋅=结论107:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则AP BP k k ⋅为定值,且有2221AP BP AM BNb k k k k e a⋅=⋅=-=-结论108:,A B 为椭圆221(0)a b a b +=>>长轴顶点,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则AN BM k k ⋅为定值,且有2221AN BM b k k e a ⋅=-=-结论109:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则AM AN k k ⋅为定值,且有()21AM AN a m k k e a m+⋅=--结论110:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则BM BN k k ⋅为定值，且有()21BM BN a m k k e a m-⋅=-+结论111:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),()E m F m m a ->,P 为椭圆任一点(非长轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EM FN k k ⋅为定值,且有222EM FNb k k a m ⋅=-+结论112:,A B 为椭圆22221(0)x y a b a b +=>>的长轴顶点,(,0),(,0),()E m F m m a ->,P 为椭圆任一点(非长轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则EN FM k k ⋅为定值,结论113:,A B 为椭圆22221(0)x y a b a b +=>>的任一直径（中心弦),P 为椭圆上任一点(不与,A B 点重合),则PA PB k k ⋅为定值,且有2221PA PBb k k e a⋅=-=-结论114:,A B 为椭圆221(0)a b a b+=>>的任一弦(不过原点且不与对称轴平行),M为弦AB 的中点,若OM k 与AB k 均存在,则OM AB k k ⋅为定值,且有2221OM ABb k k e a⋅=-=-结论115:AB 为椭圆22221(0)x y a b a b+=>>的任一弦(不与对称轴平行),若平行于AB 的弦的中点的轨迹为直线PQ ,则有2221PQ ABb k k e a⋅=-=-结论116:过椭圆22221(0)x y a b a b +=>>上任意一点(P 不是其顶点)作椭圆的切线PA ,则有2221PA OPb k k e a⋅=-=-结论117:椭圆22221(0)x y a b a b +=>>及定点(,0),()F m a m a -<<,过F 的弦的端点为A ,B ,过点A ,B 分别作直线2a x m =的垂线，垂足分别为,DC ,直线2a x m=与x 轴相交于E ,则直线AC 与BD 恒过EF 的中点,且有0AE BE k k +=.结论118:椭圆22221(0)x y a b a b +=>>及定点(,0),()F m m c =±,过F 任作一条弦,AB E 为椭圆上任一点,连接,AE BE ,且分别与准线2a x m =相交于,P Q ,则有1FP FQ k k ⋅=-结论119:椭圆22221(0)x y a b a b +=>>及定点(,0),(,0)F m a m a m -<<≠,过F 任作一条弦,AB E 为椭圆上任一点,连接AE BE 、,且分别与直线2a x m =相交于,P Q ,则有222FP FQb k k m a⋅=- 结论120:,A B 为双曲线22221(0,0)x y a b a b-=>>的顶点,P 为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则AP BP k k ⋅为定值,且有2221AP BP AM BNb k k k k e a⋅=⋅=-=结论121:,A B 为双曲线22221(0)x y a b a b +=>>的顶点,P 为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则AN BM k k ⋅为定值,且有21AN BM k k e ⋅=-结论122:,A B 双曲线22221(0)x y a b a b +=>>的顶点,P 为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m =于M N 、,则AM AN k k ⋅为定值,且有()21AM AN a m k k e a m+⋅=--结论123:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,P 为双曲线上任一点(非实轴顶点),若直线AP BP 、分别交直线2a x m =于M N 、,则BM BN k k ⋅为定值,且有()21BM BN a m k k e a m-⋅=-+结论124:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点(非实轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EM FN k k ⋅为定值,且有222EM FNb k k a m ⋅=+ 结论125:,A B 为双曲线22221(0,0)x y a b a b -=>>的顶点,(,0),(,0),(),E m F m m a P ->为双曲线上任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m=于M N 、,则EN FM k k ⋅为定值,且有222EN FMb k k a m ⋅=+ 结论126:AB 为双曲线22221(0,0)x y a b a b -=>>的任一直径,P 为双曲线上任一点(不与,A B 点重合),则PA PB k k ⋅为定值,且有2221PA PBb k k e a⋅==- 结论127:AB 为双曲线22221(0,0)x y a b a b -=>>的任一弦(不过原点且不与对称轴平行),M 为弦AB 的中点,若OM k 与AB k 均存在,则AB OM k k ⋅为定值,且有22AB OMb k k a⋅= 结论128:AB 为双曲线22221(0,0)x y a b a b-=>>的任一弦(不与对称轴平行),若平行于AB 的弦的中点的轨迹为直线PQ ,则有2221AB PQb k k e a⋅==- 结论129:过双曲线22221(0,0)x y a b a b-=>>上任意一点P (不是其顶点)作双曲线的切线PA ,则有2221PA OPb k k e a⋅==- 结论130:双曲线22221(0,0)x y a b a b -=>>及定点(,0),(F m m a >或)m a <-,过F 的弦的䇄山端点为,A B ,过,A B 分别作直线2a x m =的垂线,垂足分别为,D C ,直线2a x m=与x 轴相交于E ,则直线AC 与BD 恒过EF 的中点,且有0AE BE k k +=.结论131:双曲线22221(0,0)x y a b a b -=>>及定点(,0),()F m m c =±,过F 任作一条弦AB ,E 为双曲线上任一点,连接,AE BE ,且分别与准线2a x m =相交于,P Q ,则有1FP FQ k k ⋅=- 结论132:双曲线22221(0,0)x y a b a b-=>>及定点(,0),(F m m a >或)m a <-,过F 任作一条弦,AB E 为双曲线上任一点,连接,AE BE ,且分别与直线2a x m =相交于,P Q ,则有222FP FQb k k a m⋅=- 结论133:抛物线22(0)y px p =>及定点(,0),(0)F m m >,过F 的弦的端点为,A B 过A ,B分别作直线x m =-的垂线,垂足分别为,D C ,直线x m =-与x 轴相交于E ,则直线AC 与BD 恒过EF 的中点,且有0AE BE k k +=.结论134:抛物线22(0)y px p =>及定点(,0),2p F m m ⎛⎫=⎪⎝⎭,过F 任作一条弦,AB E 为抛物线上任一点,连接AE BE 、,分别与准线x m =-相交,P Q ,则1FP FQ k k ⋅=-结论135：抛物线22(0)y px p =>及定点(,0),(0)F m m >,过F 任作一条弦,AB E 为抛物线上任一点,连接AE BE 、分别与直线x m =-相交,P Q ,则2FP FQ p k k m⋅=-结论136:过抛物线22(0)y px p =>的焦点,02p F ⎛⎫⎪⎝⎭的弦（焦点弦）与抛物线相交于A ,B ,过B 作直线BC 与x 轴平行,且交准线于C ,则直线AC 必过原点（即其准线与x 轴交点E 与焦点F 的线段的中点).结论137:AB 为椭圆22221(0)x y a b a b+=>>的焦点F 的弦,其相应的准线与x 轴交点为E ,过A ,B 作x 轴的平行线与其相应的准线分别相交于,M N ,则直线,AN BM 均过线段EF 的中点.结论138:AB 为双曲线22221(0,0)x y a b a b-=>>的焦点F 的弦,其相应的准线与x 轴交点为E ,过A ,B 作x 轴的平行线与其相应的准线分别相交于,M N ,则直线,AN BM 均过线段EF 的中点.结论139:过圆锥物线(可以是非标准状态下)焦点弦的一个䇄山端点向其相应的准线作垂线，垂足与另一个弦的端点的连线必经过焦点到相应的准线的垂线段的中点.结论140:AB 为垂直于椭圆22221(0,0,)x y a b a b a b+=>>≠长轴上的动弦,其准线与x 轴相交于Q ,则直线AF 与BQ (或直线BF 与AQ )的交点M 必在该椭圆上.结论141:AB 为垂直于双曲线2222(0)x y a bλλ-=≠实轴的动弦,其准线与x 轴相交于Q ,则直线AF 与BQ (或直线BF 与AQ )的交点M 必在该双曲线上.结论142:AB 为垂直于抛物线2y tx =或()2(0)x ty t =≠对称轴的动弦,其准线与x 轴相交于Q ,则直线AF 与BQ (或直线BF 与AQ )的交点M 必在该抛物线上.结论143:AB 为垂直于圆锥曲线的长轴（椭圆）(或实轴（双曲线）或对称轴（抛物线)）的动弦，其准线与x 轴相交于Q ,则直线AF 与BQ (或直线BF 与AQ )的交点M 必在该圆锥曲线上.结论144:圆锥曲线的焦点弦AM (不为通径,若双曲线则为单支弦),则在x 轴上有且只有一点Q 使AQF MQF ∠=∠.结论145：过F 任作圆锥曲线的一条弦AB (若是双曲线则为单支弦),分别过,A B 作准线l 的垂线(Q 是其相应准线与x 轴的交点),垂足为11A B 、,则直线1AB 与直线1A B 都经过QF 的中点K ,即A 、1K B 、及1B K A 、、三点共线.结论146:若AM BM 、是圆锥曲线过点F 且关于长轴（椭圆）对称的两条动弦(或实轴(双曲线）或对称轴（抛物线）),则四线1111AM BN NB MA 、、、共点于K .结论147:,A B 分别为椭圆22221(0)x y a b a b +=>>的右顶点和左顶点,P 为椭圆任一点（非长轴顶点),若直线,AP BP 分别交直线2a x m=于,M N ,则以线段MN 为直径的圆必过两个定点,且椭圆外定点为2,0a Q m ⎛⎫+ ⎪ ⎪ ⎪⎝⎭及椭圆内定点为2,0a R m ⎛⎫- ⎪⎪ ⎪⎝⎭结论148:,A B 分别为双曲线22221(0,0)x y a b a b -=>>的右顶点和左顶点,P 为双曲线上任一点（非实轴顶点),若直线,AP BP 分别交直线2()a x m a m=>于,M N ,则以线段MN 为直径的圆必过两个定点,且双曲线内定点为2,0aQm⎛⎫+⎪⎪⎪⎝⎭及双曲线外定点为2,0aRm⎛⎫-⎪⎪⎪⎝⎭结论149:过直线(0)x m m=≠上但在椭圆22221(0)x ya ba b+=>>外一点M向椭圆引两条切线,切点分别为,A B,则直线AB必过定点2,0aNm⎛⎫⎪⎝⎭,且有()22222AB MNb mk ka a m⋅=-.结论150:过直线(0)x m m=≠上但在双曲线222210,0)(x ya ba b-=>>外（即双曲线中心所在区域）一点M向双曲线引两条切线,切点分别为,A B,则直线AB必过定点2,0aNm⎛⎫⎪⎝⎭,且有()22222AB MNb mk ka m a⋅=-.结论151:过直线0x m m=≠（）上但在抛物线22(0)y px p=>外（即抛物线准线所在区域)一点M向抛物线引两条切线,切点分别为,A B,则直线AB必过定点(,0)N m-,且有2AB MNpk km⋅=结论152:设点M是圆锥曲线的准线上一点（不在双曲线的渐近线上)，过点M向圆锥曲线引两条切线,切点分别为,A B,则直线AB必过准线对应的焦点F，且FM AB⊥.结论153:过直线1mx ny+=上但在椭圆22221(0)x ya ba b+=>>外一点M向椭圆引两条切线,切点分别为,A B则直线AB必过定点()22,N ma nb.结论154:过直线1mx ny+=上但在双曲线22221(0,0)x ya ba b-=>>外(即双曲线中心所在区域)一点M向双曲线引两条切线，切点分别为,A B,则直线AB必过定点()22,N ma nb.结论155:过直线10mx ny m+=≠）（上但在抛物线22(0)y px p=>外（即抛物线准线所在区域）一点M 向抛物线引两条切线,切点分别为,A B ,则直线AB 必过定点1,pn N mm ⎛⎫-- ⎪⎝⎭结论156:,A B ,是椭圆22221(0)x y a b a b+=>>的左右顶点,点P 是直线(||,0)x t t a t =≠≠上的一个动点（P 不在椭圆上),直线PA 及PB 分别与椭圆相交于,M N ,则直线MN 必与x轴相交于定点2,0a Q t ⎛⎫⎪⎝⎭.结论157:,A B 是在双曲线22221(0,0)x y a b a b-=>>的顶点,点P 是直线(||,0)x t t a t =≠≠上的一个动点(P 不在双曲线上),直线PA 及PB 分别与双曲线相交于,M N ,则直线MN 必与x 轴相交于定点2,0a Q t ⎛⎫⎪⎝⎭.结论158:,A B 是抛物线22(0)y px p =>上异于顶点O 的两个动点,若直线AB 过定点(2,0)N p ,则OA OB ⊥，且A ,B 的横坐标之积及纵坐标之积均为定值.结论159:,A B 是抛物线22(0)y px p =>上异于顶点O 的两个动点,若OA OB ⊥,则直线AB 必过定点(2,0)N p ,且,A B 的横坐标之积及纵坐标之积均为定值.结论160:,A B 是抛物线22(0)y px p =>上异于顶点O 的两个动点,若OA OB ⊥,过O 作OM AB ⊥,则动点M 的轨迹方程为2220(0)x y px x +-=≠.结论161:,A B 是抛物线22(0)y px p =>上异于顶点O 的两个动点,若OA OB ⊥,则()2min 4AOB S p ∆=结论162:过抛物线22(0)y px p =>上任一点()00,M x y 作两条弦,MA MB ,则MA MB⊥的充要条件是直线AB 过定点()002,N x p y +-结论163:过抛物线22(0)y px p =>上任一点()00,M x y 作两条弦,MA MB ,则(0)MA MB k k λλ=≠的充要条件是直线AB 过定点002,p N x y λ⎛⎫-- ⎪⎝⎭结论164:过椭圆22221(0)x y a b a b+=>>上任一点()00,M x y 作两条弦,MA MB ,则MA MB ⊥的充要条件是直线AB 过定点2222002222,a b b a N x y a b a b ⎛⎫-- ⎪++⎝⎭特别地,(1)当M 为左、右顶点时,即00,0x a y =±=时，MA MB ⊥的充要条件是直线AB 过定点()2222,0a a b N a b ⎛⎫±- ⎪ ⎪+⎝⎭（2）当M 为上、下顶点时，即000,x y b ==±时，MA MB ⊥的充要条件是直线AB 过定点()22220,b b a N b a ⎛⎫±- ⎪ ⎪+⎝⎭结论165:过双曲线22221(0,0)x y a b a b-=>>上任一点()00,M x y 作两条弦,MA MB ,则MA ⊥MB 的充要条件是直线AB 过定点2222002222,a b b a N x y a b b a ⎛⎫++ ⎪--⎝⎭特别地，当M 为左、右顶点时,即00,0x a y =±=时,MA MB ⊥的充要条件是直线AB 过定点()2222,0a a b N a b ⎛⎫±+ ⎪ ⎪-⎝⎭结论166:过二次曲线:22,,,,Ax By Cx Dy E A B C D E +++=（为常数,0A B +≠）上任一点()00,M x y 作两条弦,MA MB ,若MA MB ⊥,则直线AB 恒过定点000022,Ax C By D N x y A B A B ++⎛⎫-- ⎪++⎝⎭ 值得注意的是:在结论166中(1)令000,1,2,0A D B C p x y ====-==就是结论159;(2)令0,1,2A D B C p ====-就是结论162;(3)令22,,0A a B b C D ====就得到结论164;(4)令22,,0A b B a C D ==-==就得到结论165.。

6.P为椭圆 （a＞b＞0）上任一点,F1,F2为二焦点，A为椭圆一定点，则 ,当且仅当 三点共线时，等号成立.
7.椭圆 与直线 有公共点的充要条件是 .
8.已知椭圆 （a＞b＞0），O为坐标原点，P、Q为椭圆上两动点，且 .（1） ;（2）|OP|2+|OQ|2的最大值为 ;（3） 的最小值是 .
14.过椭圆焦半径的端点作椭圆的切线，与以长轴为直径的圆相交，则相应交点与相应焦点的连线必与切线垂直.
15.过椭圆焦半径的端点作椭圆的切线交相应准线于一点，则该点与焦点的连线必与焦半径互相垂直.
16.椭圆焦三角形中,点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
（注:在椭圆焦三角形中,非焦顶点的、外角平分线与长轴交点分别称为、外点.）
3.以焦点弦PQ为直径的圆必与对应准线相交.
4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.（切：P在右支；外切：P在左支）
5.若 在双曲线 （a＞0,b＞0）上，则过 的双曲线的切线方程是 .
6.若 在双曲线 （a＞0,b＞0）外 ，则过Po作双曲线的两条切线切点为P1、P2，则切点弦P1P2的直线方程是 .
3.以焦点弦PQ为直径的圆必与对应准线相离.
4.以焦点半径PF1为直径的圆必与以长轴为直径的圆切.
5.若 在椭圆 上，则过 的椭圆的切线方程是 .
6.若 在椭圆 外 ，则过Po作椭圆的两条切线切点为P1、P2，则切点弦P1P2的直线方程是 .
7.椭圆 (a＞b＞0)的左右焦点分别为F1，F2，点P为椭圆上任意一点 ，则椭圆的焦点角形的面积为 .
9.过椭圆 （a＞b＞0）的右焦点F作直线交该椭圆右支于M,N两点，弦MN的垂直平分线交x轴于P，则 .

有关圆锥曲线的经典结论★说明：圆锥曲线我们并未学完,有些内容（如焦半径公式），将此资料发到群里是想让大家在日常学习过程中自我感悟使用，不要过分纠结于此!有关解析几何的经典结论一、椭 圆1. 点P 处的切线ＰＴ平分△PF １F 2在点P 处的外角.2. PT 平分△ＰF 1F ２在点P 处的外角,则焦点在直线P Ｔ上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点....文档交流 仅供参考... 3. 以焦点弦PQ 为直径的圆必与对应准线相离。

4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切．5. 若000(,)P x y 在椭圆22221x y a b +=上，则过0P 的椭圆的切线方程是00221x x y ya b +=.6. 若000(,)P x y 在椭圆22221x y a b+=外 ，则过Ｐo 作椭圆的两条切线切点为P １、P ２，则切点弦Ｐ1Ｐ2的直线方程是00221x x y ya b+=．7. 椭圆22221x y a b+= (ａ〉b ＞0）的左右焦点分别为F 1，F 2，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=（a ＞b ＞０）的焦半径公式：10||MF a ex =+,20||MF a ex =-（1(,0)F c - ， 2(,0)F c 00(,)M x y ）.9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点，则MF ⊥N Ｆ....文档交流 仅供参考...10. 过椭圆一个焦点F 的直线与椭圆交于两点Ｐ、Q ， A 1、A 2为椭圆长轴上的顶点,A 1Ｐ和A 2Q 交于点Ｍ，A 2Ｐ和A １Q 交于点N ，则ＭF ⊥NF 。

...文档交流 仅供参考...11. A Ｂ是椭圆22221x y a b +=的不平行于对称轴的弦,Ｍ),(00y x 为AB 的中点，则22OM AB b k k a ⋅=-，即0202y a x b K AB -=.12. 若000(,)P x y 在椭圆22221x y a b+=内，则被Ｐo 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+. 13. 若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+． 二、双曲线1. 点P 处的切线PT 平分△ＰF 1F 2在点P 处的内角。

圆锥曲线的一些经典结论1. 圆锥曲线有四种类型：椭圆、抛物线、双曲线和圆。

2. 椭圆：椭圆是圆锥曲线的一种，它由离心率小于1的点构成。

椭圆具有两个焦点和一个长轴和短轴。

3. 抛物线：抛物线是圆锥曲线的一种，它具有一个焦点和一个直线作为其轴线。

所有的点到焦点的距离都等于其到轴线的距离。

4. 双曲线：双曲线是圆锥曲线的一种，它由离心率大于1的点构成。

双曲线具有两个焦点和两个分离的曲线枝。

5. 圆：圆是圆锥曲线的一种特殊情况，它的离心率为零，所有的点到圆心的距离相等。

6. 圆锥曲线的方程：圆锥曲线可以通过方程来表示。

例如，椭圆的标准方程为(x-h)²/a² + (y-k)²/b² = 1，其中(h,k)是椭圆的中心点，a 和b分别是长轴和短轴的长度。

7. 长轴和短轴：圆锥曲线具有两个轴，它们都通过曲线的中心点。

长轴是椭圆或双曲线的主轴，它的长度是贯穿曲线的最长距离。

短轴是与长轴垂直的轴，它的长度是贯穿曲线的最短距离。

8. 离心率：离心率是一个非常重要的指标，用来描述圆锥曲线的形状。

离心率通常用字母e表示，可以通过离心率的定义公式e =c/a来计算，其中c是焦点离中心的距离，a是长轴的长度。

9. 集点定理：集点定理是圆锥曲线研究的基本定理之一。

它表明，对于一个椭圆或双曲线，所有点到两个焦点的距离之和是常数，等于长轴的长度。

10. 曲率：曲率是描述曲线弯曲程度的属性。

圆锥曲线的曲率在不同点上有不同的值，它可以通过曲线的方程来计算。

这些是圆锥曲线的一些经典结论，它们是圆锥曲线理论的基础，可以应用在许多科学和工程领域，如天文学、物理学和工程学等。

数学圆锥曲线重要结论|高考圆锥曲线秒杀结论
圆锥曲线的相关内容是平面解析几何的核心,是支撑中学数学学科知识体系的主要内容,下面是为你整理的数学圆锥曲线重要结论，一起来看看吧。

数学圆锥曲线重要结论(一)
数学圆锥曲线重要结论(二)
数学圆锥曲线重要结论(三)
猜你感兴趣的：
1.高二数学选修1-1圆锥曲线知识点
2.数学高考题圆锥曲线题解题套路分析
3.高中数学圆锥曲线论文
4.20__高考数学圆锥曲线复习方法
5.关于数学文化的论文优秀范文
第 1 页共 1 页。