长方体的表面积的计算方法

长方体面积公式计算公式长方体是一种常见的几何体，它具有六个面，分别是上下底面、前后面和左右两侧面。

计算长方体的面积是一项基础的几何运算，而长方体面积公式可以帮助我们准确地求解长方体的表面积。

长方体的面积公式是通过对长方体的各个面进行测量和计算得出的。

根据几何原理，长方体的上下底面积相等，为长方体的长乘以宽；前后面的面积也相等，为长方体的长乘以高；左右两侧面积也相等，为长方体的宽乘以高。

因此，我们可以得出长方体的表面积公式如下：长方体的表面积= 2 × (长× 宽 + 长× 高 + 宽× 高)通过这个公式，我们可以计算出任意长方体的表面积。

下面，我将通过实际例子来展示如何应用长方体面积公式进行计算。

假设我们有一个长方体，它的长为5cm，宽为3cm，高为4cm。

现在，我们来计算一下这个长方体的表面积。

根据长方体面积公式，我们可以将长、宽和高代入公式中进行计算。

首先，计算长方体的上下底面积，即5cm × 3cm = 15cm²；然后，计算前后面的面积，即5cm × 4cm = 20cm²；最后，计算左右两侧面的面积，即3cm × 4cm = 12cm²。

将这三个面的面积相加，即可得到长方体的表面积。

长方体的表面积= 2 × (15cm² + 20cm² + 12cm²) = 2 × 47cm² = 94cm²所以，这个长方体的表面积为94cm²。

通过这个例子，我们可以看到，通过长方体面积公式，我们可以准确地计算出长方体的表面积。

这个公式的应用非常广泛，不仅可以用于计算长方体的表面积，还可以应用于其他几何体的表面积计算，比如正方体、圆柱体等。

长方体面积公式的应用不仅仅局限于数学课堂，它在日常生活中也有很多实际应用。

比如，我们可以通过计算长方体的表面积来确定包装盒的大小，以确保物品能够完全放入盒子中；在建筑设计中，我们也需要计算房间的表面积，以确定装修材料的用量等。

长方体表面面积公式长方体是我们日常生活中经常接触到的一种立体图形，它的形状如同一个长方形的盒子，有着六个面，包括上下两个底面和四个侧面。

我们可以通过计算长方体的表面积来了解这个立体图形的大小和形状，而长方体表面面积公式则是用来计算长方体表面积的重要工具。

长方体的表面积是指长方体各个面的总面积，包括上下两个底面和四个侧面的面积。

为了方便计算，我们可以将长方体拆分成若干个矩形，然后计算每个矩形的面积，最后将所有矩形的面积相加即可得到长方体的表面积。

长方体表面面积公式为：S = 2ab + 2bc + 2ac，其中a、b、c分别为长方体的三条边长。

这个公式的推导可以通过将长方体拆分成若干个矩形来实现。

具体地，我们可以将长方体拆分成两个上下底面和四个侧面，每个面都是一个矩形。

上下底面的面积为ab，共有两个，因此上下底面的面积之和为2ab。

同理，侧面可以拆分成bc、ac 两个矩形，每个矩形的面积为bc和ac，共有两个侧面，因此侧面的面积之和为2bc + 2ac。

将上下底面和侧面的面积相加，即可得到长方体的表面积。

长方体表面面积公式的应用非常广泛。

在日常生活中，我们可以用这个公式来计算长方体的表面积，如计算一个长方形盒子的表面积，以确定包装费用或材料数量。

在工程和建筑领域，长方体表面面积公式也被广泛应用。

例如，在设计房屋或建筑物时，建筑师需要计算墙壁、地板和天花板等表面的面积，以确定建筑材料的数量和成本。

在工业生产中，长方体表面面积公式也被广泛应用，如计算容器或管道的表面积，以确定涂层或绝缘材料的用量。

总之，长方体表面面积公式是计算长方体表面积的重要工具，它的应用范围非常广泛，包括日常生活、工程建筑和工业生产等领域。

掌握这个公式可以帮助我们更好地理解长方体的形状和大小，为我们的生活和工作带来便利。

长方体和正方体表面积计算公式长方体和正方体是我们生活中常见的几何体，无论是在建筑、设计、制造还是日常生活中，都有广泛的应用。

在计算长方体和正方体的表面积时，我们需要根据其特定的公式进行计算。

本文将介绍长方体和正方体的表面积计算公式及其应用。

一、长方体表面积计算公式长方体是一种具有六个矩形面的立体几何体，其表面积的计算公式为：长方体表面积 = 2(长×宽 + 长×高 + 宽×高)其中，长、宽、高分别代表长方体的三个边长。

上述公式中，2表示长方体的前后两个面、左右两个面、上下两个面，共六个面，每个面的面积都是长乘宽，因此需要将其相加。

例如，如果一个长方体的长、宽、高分别为3厘米、4厘米、5厘米，则其表面积为：长方体表面积 = 2(3 × 4 + 3 × 5 + 4 × 5) = 2(12 + 15 +20) = 94平方厘米二、正方体表面积计算公式正方体是一种具有六个正方形面的立体几何体，其表面积的计算公式为：正方体表面积 = 6 ×边长其中，边长代表正方体的边长。

上述公式中，6表示正方体有六个面，每个面的面积都是边长的平方，因此需要将其相加。

例如，如果一个正方体的边长为3厘米，则其表面积为：正方体表面积 = 6 × 3 = 6 × 9 = 54平方厘米三、长方体和正方体表面积的应用长方体和正方体的表面积计算公式在实际生活中有广泛的应用。

以下是一些例子：1. 在建筑设计中，建筑师需要计算建筑物的表面积，以确定需要使用的建筑材料的数量和成本。

例如，一个长方体的房间的墙壁和天花板的表面积可以用长方体表面积的公式来计算。

2. 在制造业中，工程师需要计算机器和设备的表面积，以确定需要使用的材料的数量和成本。

例如，一个正方体的箱子的表面积可以用正方体表面积的公式来计算。

3. 在日常生活中，我们可以用长方体和正方体表面积的公式来计算一些日常用品的表面积。

长方体的表面积知识点长方体是一个有六个矩形面的立体图形，其中每个矩形面的边长分别为a、b和c。

长方体的表面积是指所有矩形面的面积之和。

在本文中，我们将详细讨论长方体的表面积计算公式以及相关的应用。

1.长方体的表面积计算公式长方体的表面积计算公式是：2(ab + ac + bc)。

根据这个公式，我们可以得出长方体表面积与长、宽、高之间的关系。

2.实例演算为了更好地理解长方体表面积的计算方法，我们以一个具体的实例来演算。

假设长方体的长为5cm，宽为3cm，高为4cm。

根据表面积计算公式，我们可以计算出长方体的表面积。

表面积 = 2(5*3 + 5*4 + 3*4) = 2(15 + 20 + 12) = 2(47) = 94因此，这个长方体的表面积为94平方厘米。

3.表面积的意义和应用长方体的表面积是对长方体所占用的空间进行度量的一种方式。

它在现实生活中有许多应用。

以下是一些例子：a.建筑领域：在建筑设计中，计算建筑物的表面积可以帮助工程师确定需要的材料数量，从而预估成本和工期。

b.包装设计：在产品包装设计中，计算物体的表面积可以帮助设计师优化包装的形状和大小，从而节省材料和最大化存储空间。

c.装饰设计：在室内装饰设计中，计算墙面、地板和天花板的表面积可以帮助设计师确定所需的涂料和壁纸数量，以及地板和瓷砖的铺设。

d.计算容量：在物体容量计算中，表面积可以提供一些线索。

例如，如果我们知道一个长方体的表面积和其中一个维度，我们可以使用表面积计算公式来解决未知的维度。

4.表面积与体积的区别需要注意的是，长方体的表面积和体积是不同的概念。

表面积是对长方体外部的度量，而体积是对长方体内部空间的度量。

表面积是一个二维度量，通常用平方单位来表示，如平方厘米（cm²），平方米（m²）等。

而体积是一个三维度量，通常用立方单位来表示，如立方厘米（cm³），立方米（m³）等。

5.其他立体图形的表面积计算除了长方体，其他一些常见的立体图形的表面积也可以通过类似的方法进行计算。

长方体五个面的表面积公式篇一：长方体有五个面，每个面都是一个长方形。

计算长方体五个面的表面积时，可以使用以下公式:表面积 = 2 × (长面面积 + 宽面面积 + 高面面积)其中，长面、宽面、高面分别指长方体的一个长面、一个宽面和一个高面。

长方体的各个面的特征如下:- 长面：通常是长方形，长度是长方体的长度。

- 宽面：通常是长方形，宽度是长方体的宽度。

- 高面：通常是长方形，高度是长方体的高度。

根据长方体的特征，可以推导出长方体表面积的公式:表面积 = 2 × (长面面积 + 宽面面积 + 高面面积)= 2 × (长度×宽度 + 长度×高度 + 宽度×高度)= 2 × (长度×宽度 + 宽度×高度 + 长度×高度)= 2 × (长度 + 宽度 + 高度) ×长度×宽度= (长度 + 宽度 + 高度) × 2 ×长方体的长度×宽度因此，长方体五个面的表面积公式可以表示为:表面积 = (长面面积 + 宽面面积 + 高面面积) ×长方体的长度×宽度拓展：长方体表面积的计算方法计算长方体的表面积时，可以使用多种方法。

其中，最常见的方法是使用公式计算法，也称为“面积公式法”。

方法一：面积公式法1. 确定长方体的长、宽、高，并计算出每个面的面积。

2. 将每个面的面积乘以长方体的长、宽、高，得到总表面积。

方法二：折叠法1. 将长方体展开，并折叠成一个平面图形。

2. 计算每个面的面积，并将所有面积相加得到长方体的表面积。

无论使用哪种方法，计算长方体的表面积都需要一定的数学知识和技巧。

在实际生产和生活中，人们常常需要快速、准确地计算长方体的表面积，因此需要熟悉各种表面积计算方法和技巧。

篇二：长方体是由三个轴对称的平面组成的三维多面体，因此它有五个面。

长方体的表面积推导公式
在几何学中，长方体是一种具有六个面的立体图形，其中每个面都是长方形。

计算长方体的表面积是一项重要的几何问题，其常用的推导公式为：
长方体的表面积 = 2lw + 2lh + 2wh
其中，l、w、h分别表示长方体的长度、宽度和高度。

这个公式可以理解为将长方体展开成6个长方形，然后计算每个长方形的面积，最后将它们加起来。

例如，一个长方体的长为5cm，宽为4cm，高为3cm，那么根据
上述公式，其表面积为：
2 × 5 × 4 + 2 × 5 ×
3 + 2 ×
4 × 3 = 94（平方厘米）
这个公式也可以简化为：
长方体的表面积 = 2lw + 2lh + 2wh = 2(lw + lh + wh)
无论是哪种形式，这个公式都是计算长方体表面积的基本工具，对于工程、建筑等领域的计算都有广泛应用。

- 1 -。

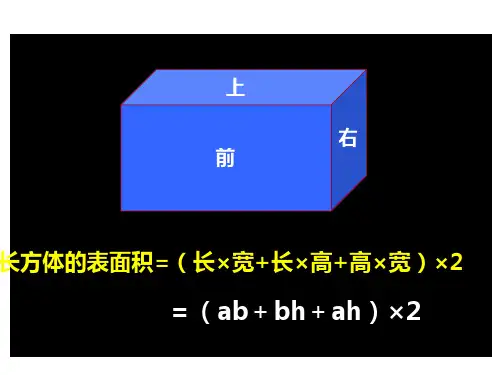
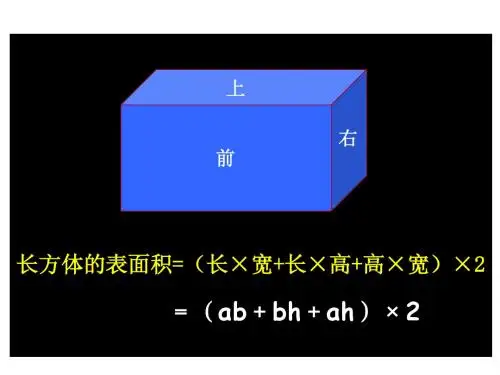
长方体的表面积
（1）前面的面积＝后面的面积＝长×高，
左面的面积＝右边的面积＝宽×高，
上面的面积＝下面的面积＝长×宽。

所以，长方体的表面积＝(前面的面积＋右面的面积＋上面的面积)×2
长方体的表面积＝（长×高＋宽×高＋长×宽）×2
通常我们用字母a表示长，用字母b表示宽，用字母h表示高，用S表示图形的面积。

长方体的表面积是：S＝2（ah＋bh＋ab）。

（2）长方体的表面积=侧面积+底面积×2
侧面积=底面周长×高
长方形的表面积=底面周长×高＋底面积×2
正方体的表面积
正方体的表面积是指围成正方体的6个正方形的面积之和，也就是说，要求一个正方体的表面积，我们只需要求出正方体的一个面的面积，再乘6就可以了。

正方体的表面积＝棱长×棱长×6
通常我们用字母a表示正方体的棱长，用S表示正方体的表面积，所以正方体的表面积是：
S＝6a²。

长方体表面面积公式长方体是我们日常生活中常见的一个几何体。

它有六个面，分别是两个底面和四个侧面。

这六个面中，除了底面是相同的矩形，其它的五个面都是相同的长方形。

想要计算长方体的表面积，我们需要知道各个面的面积，并将它们加起来。

长方体表面积的公式是：S=2ab+2ac+2bc，其中a、b、c分别代表长方体的三个棱长。

根据公式，我们可以把长方体表面积分成三部分。

第一部分是两个底面的面积，每个底面的面积都是ab。

由于底面相同，所以两个底面的面积相加就是2ab。

第二部分是长方体前后面以及左右两侧面的面积。

这四个面的面积都相等，都为ac，bc。

所以这部分的表面积应该是2ac+2bc。

第三部分是长方体上下两个面的面积。

这两个面的面积也相等，都为ab。

所以这部分的表面积也是2ab。

通过这个公式，我们可以为各种长方体计算表面积。

例如一个长方体的棱长分别为3 cm、4 cm和5 cm，那么它的表面积就是2×3×4+2×3×5+2×4×5=94 (cm²)。

也就是说，这个长方体的表面积是94平方厘米。

除此之外，这个公式也可以拓展到其他类似的几何体。

例如，如果我们希望计算正方体的表面积，即六个面中每个面都是正方形，那么我们可以将a、b、c这三个棱长看成相等的边长s。

这样，公式就变成了S=6s²。

当然，在计算长方体表面积时，还有一些可以简化的优化。

比如我们可以把公式写成S=2（ab+ac+bc），这样的话就可以省略重复计算两次的2ab。

另外，如果长方体的两个棱长相等，那么其中的一些项也可以简化。

总的来说，长方体表面积公式是一种非常重要的数学知识。

在我们进行日常生活、学术研究和工程设计等场景下都有广泛的应用。

通过熟练掌握这个公式，我们不仅可以准确地计算长方体的表面积，也能更好地理解其它几何体的表面积。