下载文档原格式
17世纪的一位法国数学家，提出了一个数学难题，使得后来的数学家一筹莫展，这个人就是费马(1601——1665)。
这道题是这样的：当n>2时，x^n+y^n=z^n没有正整数解。
在数学上这称为“费马大定理”。
为了获得它的一个肯定的或者否定的证明，历史上几次悬赏征求答案，一代又一代最优秀的数学家都曾研究过，即使用现代的电子计算机也只能证明：当n小于等于4100万时，费马大定理是正确的。
由于当时费马声称他已解决了这个问题，但是他没有公布结果，于是留下了这个数学难题中少有的千古之谜。
费马小传：费马（1601～1665）Fermat，Pierre de费马是法国数学家，1601年8月17日出生于法国南部图卢兹附近的博蒙·德·洛马涅。
他的父亲多米尼克·费马在当地开了一家大皮革商店，拥有相当丰厚的产业，使得费马从小生活在富裕舒适的环境中。
费马的父亲由于富有和经营有道，颇受人们尊敬，并因此获得了地方事务顾问的头衔，但费马小的时候并没有因为家境的富裕而产生多少优越感。
费马的母亲名叫克拉莱·德·罗格，出身穿袍贵族。
多米尼克的大富与罗格的大贵族构筑了费马极富贵的身价。
费马小时候受教于他的叔叔皮埃尔，受到了良好的启蒙教育，培养了他广泛的兴趣和爱好，对他的性格也产生了重要的影响。
直到14岁时，费马才进入博蒙·德·洛马涅公学，毕业后先后在奥尔良大学和图卢兹大学学习法律。
17 世纪的法国，男子最讲究的职业是当律师，因此，男子学习法律成为时髦，也使人敬羡。
有趣的是，法国为那些有产的而缺少资历的“准律师”尽快成为律师创造了很好的条件。
1523年，佛朗期瓦一世组织成立了一个专门鬻卖官爵的机关，公开出售官职。
这种官职鬻卖的社会现象一经产生，便应时代的需要而一发不可收拾，且弥留今日。
鬻卖官职，一方面迎合了那些富有者，使其获得官位从而提高社会地位，另一方面也使政府的财政状况得以好转。
业余数学家之王费马的名人故事
17世纪的一位法国数学家，提出了一个数学难题，使得后来的数学家一筹莫展，这个人就是费马(1601—1665)。
这道题是这样的：当n>2时，xn+yn=zn没有正整数解。
在数学上这称为“费马大定理”。
为了获得它的一个肯定的或者否定的证明，历史上几次悬赏征求答案，一代又一代最优秀的数学家都曾研究过，但是300多年过去了，至今既未获得最终证明，也未被推翻。
即使用现代的电子计算机也只能证明：当n小于等于4100万时，费马大定理是正确的。
由于当时费马声称他已解决了这个问题，但是他没有公布结果，于是留下数学难题中少有的千古之谜。
费马生于法国南部，在大学里学的是法律，以后以律师为职业，并被推举为议员。
费马的业余时间全用来读书，哲学、文学、历史、法律样样都读。
30岁时迷恋上数学，直到他64岁病逝，一生中有许多伟大的发现。
不过，他极少公开发表论文、著作，主要通过与友人通信透露他的思想。
在他死后，由儿子通过整理他的笔记和批注挖掘他的思想。
好在费马有个“不动笔墨不读书”的习惯，凡是他读过的书，都有他的圈圈点点，勾勾画画，页边还有他的评论。
他利用公务之余钻研数学，并且成果累累。
后世数学家从他的'诸多猜想和大胆创造中受益非浅，赞誉他为“业余数学家之王”。
费马对数学的贡献包括：与笛卡尔共同创立了解析几何；创造了作曲线切线的方法，被微积分发明人之一牛顿奉为微积分的思想先驱；通过提出有价值的猜想，指明了关于整数的理论——数论的发展方向。
他还研究了掷骰子的输赢规律，从而成为古典概率论的奠基人之一。
费马编辑词条费马费马(Pierre de Fermat，1601～1665）法国著名数学家，被誉为“业余数学家之王”。
他自己证明了他的大定理，他是先用毕达哥拉斯方程的通解公式证明这个毕氏公式中的数X，Y，Z无大于2的同次幂数存在，再把他的定理的不等式公式无穷递降到2次方时可以发现，他的不等式公式为二次方时，不等式中的数X，Y，Z都是同次幂数，而毕达哥拉斯方程中的数X，Y，Z不是同次幂数，这时用比较法完全可以判定他的定理成立。
目录人物简介人物生平主要贡献错误贡献评价展开编辑本段人物简介费马生性内向，谦抑好静，不善推销自己，不善展示自我。
因此他生前极少发表自己的论著，连一部完整的著作也没有出版。
他发表的一些文章，也总是隐姓埋名。
《数学论集》还是费马去世后由其长子将其笔记、批注及书信整理成书而出版的。
我们现在早就认识到时间性对于科学的重要，即使在l7世纪，这个问题也是突出的。
费马的数学研究成果不及时发表，得不到传播和发展，并不完全是个人的名誉损失，而是影响了那个时代数学前进的步伐。
对费马来说，真正的事业是学术，尤其是数学。
费马通晓法语、意大利语、西班牙语、拉丁语和希腊语，而且还颇有研究。
语言方面的博学给费马的数学研究提供了语言工具和便利，使他有能力学习和了解阿拉伯和意大利的代数以及古希腊的数学。
正是这些，可能为费马在数学上的造诣莫定了良好基础。
在数学上，费马不仅可以在数学王国里自由驰骋，而且还可以站在数学天地之外鸟瞰数学。
这也不能绝对归于他的数学天赋，与他的博学多才多少也是有关系的。
编辑本段人物生平幼年生活费马（也译为“费尔马”）1601年8月17日出生于法国南部图卢兹附近的博蒙·德·洛马涅。
他的父亲多米尼克·费马在当地开了一家大皮革商店，拥有相当丰厚的产业，使得费马从小生活在富裕舒适的环境中。
费马的父亲由于富有和经营有道，颇受人们尊敬，并因此获得了地方事务顾问的头衔，但费马小的时候并没有因为家境的富裕而产生多少优越感。
费马-业余数学家之王费马1601年8月17日出生于法国南部图卢兹附近的博蒙·德·洛马涅。
他的父亲多米尼克·费马在当地开了一家大皮革商店，拥有相当丰厚的产业，使得费马从小生活在富裕舒适的环境中。
费马的父亲由于富有和经营有道，颇受人们尊敬，并因此获得了地方事务顾问的头衔，但费马小的时候并没有因为家境的富裕而产生多少优越感。
费马的母亲名叫克拉莱·德·罗格，出身穿袍贵族。
多米尼克的大富与罗格的大贵族构筑了费马极富贵的身价。
费马小时候受教于他的叔叔皮埃尔，受到了良好的启蒙教育，培养了他广泛的兴趣和爱好，对他的性格也产生了重要的影响。
直到14岁时，费马才进入博蒙·德·洛马涅公学，毕业后先后在奥尔良大学和图卢兹大学学习法律。
费马尚没有大学毕业，便在博蒙·德·洛马涅买好了“律师”和“参议员”的职位。
等到费马毕业返回家乡以后，他便很容易地当上了图卢兹议会的议员，时值1631年。
尽管费马从步入社会直到去世都没有失去官职，而且逐年得到提升，但是据记载，费马并没有什么政绩，应付官场的能力也极普通，更谈不上什么领导才能。
不过，费马并未因此而中断升迁。
在费马任了七年地方议会议员之后，升任了调查参议员，这个官职有权对行政当局进行调查和提出质疑。
费马的婚姻使费马跻身于穿袍贵族的行列，费马娶了他的舅表妹露伊丝·德·罗格。
原本就为母亲的贵族血统而感骄傲的费马，如今干脆在自己的姓名上加上了贵族姓氏的标志“de”。
费马生有三女二男，除了大女儿克拉莱出嫁之外，四个子女都使费马感到体面。
两个女儿当上了牧师，次子当上了菲玛雷斯的副主教。
尤其是长子克莱曼特·萨摩尔，他不仅继承了费马的公职，在1665年当上了律师，而且还整理了费马的数学论著。
如果不是费马长子积极出版费马的数学论著，很难说费马能对数学产生如此重大的影响，因为大部分论文都是在费马死后，由其长子负责发表的。
费马和笛卡尔都是解析几何的发明者解析几何建立的故事一句话，科学的需要和对方法论的兴趣，推动了费尔马和笛卡尔对坐标几何的研究。
费马出身于商人家庭，他是学法律的，职业是律师，数学只是他的业余爱好。
虽然他只能利用工作之余的闲暇时间研究数学，但他对数论和微积分的研究都做出了第一流的贡献。
他还同帕斯卡一同开创了概率论的研究工作，他和笛卡尔也都是解析几何的发明者。
费马关于曲线的研究是从研究古希腊几何学家，特别是阿波罗尼的论著开始的。
当时阿波罗尼的《论平面轨迹》一书已失传很久了，是费马又把它重新写出来的人之一。
他用代数方法来研究曲线。
他说，他打算发起一个关于轨迹的一般研究，在这种研究是古希腊人没做到的。
1629年他写了一本《平面和立体的轨迹引论》，是在1679年发表的。
他在书中说，他找到了一个研究有关曲线问题的普遍方法。
我们并不清楚费马的坐标几何研究怎样产生的，很有可能他是把阿波罗尼的结果直接翻译成代数的形式。
他考虑任意曲线和它上面的一般点J，J的位置用A、E两个字母定出：A是从原点O沿底线到点Z的距离，E是从Z到J的距离。
它所用的坐标，就是我们现在的斜坐标。
但是Y轴没有明白出现，而且不用负数，它的A，E就是我们现在的X、Y。
费马把他的一般原理，叙述为“只要在最后的方程里出现两各未知量，我们就得到一个轨迹，这两个量之一，其末端描绘出一条直线或曲线。
“前面说的对不同位置的E，其末端J，J‘，J’‘……就把“线”描出，它的未知量A和E，实际是变数。
或者可以说，联系A和E的方程是不定的。
他写出联系A、E的各种方程，并指明它们所描绘的曲线。
例如，他给出方程（用我们现在的写法就是）d x = b y，并指出这代表一条直线。
他又给出d (a-x) = b y,并指出它也表示一条直线。
方程p2-x2 = y2代表一个圆。
a2+x2 = k y2和xy = a 各代表一条双曲线，x2 = ay代表一条抛物线，而且费马确实领悟到坐标轴可以平移和旋转。
费马大定理简介费马大定理，又被称为费马最后定理或费马猜想，是数学界的一个重要问题。
它是由17世纪法国数学家费尔马在1637年提出的，直到1994年才被英国数学家安德鲁·怀尔斯证明，被认为是数学史上最著名的定理之一。
费马大定理的表述非常简洁，即：对于任何大于2的整数n，方程x^n + y^n = z^n没有正整数解。
在费马提出这个猜想后的几百年里，许多数学家都尝试过证明它，但都以失败告终，直到怀尔斯的证明出现，才彻底解决了这个问题。
费马大定理的证明过程非常复杂，涉及到许多高深的数学知识。
怀尔斯使用了现代代数几何学、模形式和椭圆曲线等数学分支的理论和方法，最终完成了对费马大定理的证明。
他的证明被广泛认可，赢得了数学界的高度赞誉，也为他赢得了1994年的菲尔兹奖，这是数学界最高荣誉。
费马大定理的证明对数学的发展产生了巨大的影响。
它不仅填补了数学史上的一个重要空白，而且也推动了许多相关领域的发展。
例如，怀尔斯证明费马大定理所使用的工具和方法，对于椭圆曲线密码学的发展起到了重要的作用。
此外，费马大定理的证明还鼓舞了许多数学家攻克其他难题的信心，推动了整个数学领域的研究。
费马大定理的证明不仅仅是一个数学问题的解决，它还具有哲学和历史的意义。
费马大定理的提出和证明过程，展示了人类对于数学的追求和智慧的体现。
它也向世人展示了数学的美丽和深度，激发了人们对数学的兴趣和热爱。
尽管费马大定理已经被证明，但它的证明过程仍然具有很高的难度。
对于普通人来说，理解费马大定理的证明需要具备相当高的数学知识和能力。
然而，即使没有深入的数学知识，我们仍然可以欣赏这个定理的重要性和它对数学发展的巨大贡献。
费马大定理的解决是数学界的一项伟大成就，它不仅证明了费马的猜想，也为数学的研究和应用开辟了新的方向。
它告诉我们，数学是一门充满挑战和乐趣的学科，它的发展推动了人类的进步和创新。
费马大定理的证明是数学史上的一个里程碑，它让我们深刻认识到数学的力量和奇妙之处。
业余数学之王——费马我们都知道，法国几百年来一直盛产数学家，而且从未间断，这就是法国数学可以经久不衰的根源所在。
法国近代数学的发展可以追溯到十七世纪，这一时期正是科学复兴和发展的时候，而法国数学界则诞生了笛卡尔和费马等伟大的数学家。
而今天所介绍的是被称为“业余数学之王”的费马。
费马费马(Pierre de Fermat，1601~1665)是法国著名数学家，出生于法国南部的图卢兹地区，父亲是家产丰厚的皮革商人，后来还到政府就职，而母亲则是当地一名议会法官的女儿。
费马的家庭条件十分优渥，这就让他从小有机会接受良好的教育。
和当时的传统一样，费马青少年时期接受的是家庭教育，不过比较遗憾的是，没有任何资料记录了费马这段时间内的学习情况。
大约在14岁时，费马到进入图卢兹的学校学习法律。
费马选择学习法律不仅仅是因为家庭的影响，也是当时法国社会的风气，在当时的法国人看来，成为律师或法官是一件非常荣耀的事。
1631年，三十岁的费马进入图卢兹政府就职，此后一生中费马一路升迁，不过这倒不是因为他政绩突出，实际上以当时的资料来看，费马的管理水平和施政水平都很一般，谈不上有什么突出的成绩。
真正使得他得以升迁的除了他的贵族身份外，更多的是因为他历来廉洁奉公，真诚待人，这赢得了许多人的爱戴。
直到去世，费马都在政府部门兢兢业业工作，只在工作之余才花时间在感兴趣的数学上，这也正是费马被称“业余数学之王”的原因。
和同时代的其他数学家相比，费马的一生十分平静，没有什么大起大落，显得波澜不惊。
费马和自己的表妹结婚后，育有三儿两女，这些子女后来的境遇都使费马感到满意，尤其是他的大儿子克莱蒙。
克莱蒙几乎继承了费马的身份和公职，最重要的是，克莱蒙在费马去世以后花费大量时间精力整理出版他父亲在几十年里完成的研究笔记，否则，费马的工作将永远石沉大海，再无问世的可能。
1665年1月12日，在处理完卡斯特雷城的一个案子后，费马因病去世，结束了他平静、诚实、正直的一生。
费马定理费马原理是光学中最为基础的原理,它在物理学发展的历程中有着至关重要的作用。
它用一种新的看法将几何光学的三个基本实验定律（光的反射定律和折射定律、光的独立传播定律光的直线传播定律直线传播）进行统一,并表述了三者的联系。
通过研究几何光学问题，能彰显出费马定理的重要性，能更加系统化光学理论.可见通过费马原理推导上述三个基本实验定律,能使我们更加系统的理解光学理论，这对广大学者都有着不可或缺的意义。
费马原理的直观表达：光从空间的一点到另一点的实际路径是沿着光程为极值的路径传播的。
或者说， 光沿着光程为极大、极小或者常量的路径传播。
光线从Q 点传播到P 点所需的总时间：⎰∑∑=∆=∆===ndl c t l n c v l t PQ i i i i i i 1111费马原理：在所有可能的光传播路径中，实际路径所需的时间 取极值。
⎰==01ndl ct P Q δδ 在光传播的所有可能存在的路径中，其实际路径所对应的光程取极致。
⎰==0ndl L P Q δδ① 直线传播定律:两点间的所有可能连线中，线段最短-—光程取极小值。
② 内椭球面的反射： 椭球面上任一点到两个焦点连线的角平分线即过该点的面法线，且两线段长度之和相等。
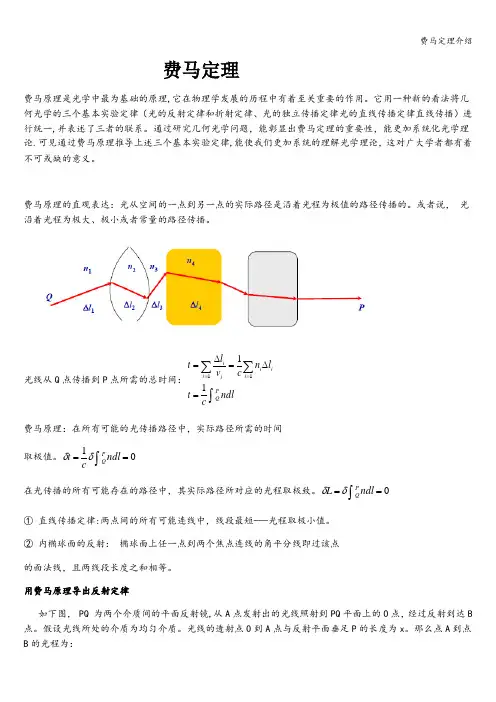
用费马原理导出反射定律如下图， PQ 为两个介质间的平面反射镜,从A 点发射出的光线照射到PQ 平面上的O 点，经过反射到达B 点。
假设光线所处的介质为均匀介质。
光线的透射点O 到A 点与反射平面垂足P 的长度为x 。
那么点A 到点B 的光程为：()⎥⎦⎤⎢⎣⎡-+++=222221x a H x H n OBn AO n L +=()22222211x a H n x H n -+++=OBn AO n L 21+=很明显，光程L 是关于变量x 的函数,由费马原理分析，真实的光程是固定的,在均匀介质中的一阶导数是0，即()()0222221=-+--+=x a H x a n x H nx dx dL即有()I n I n -sin sin =即I I -=反射定律由上面推导出来了.进一步可以证明22dxL d >0 ， 这说明满足反射定律的光线具有最短光程. 从费马原理导出折射定律下图中，两个介质均为均匀介质，它们的折射率分别为1n 、2n ，光线从1n 介质投射到折射面的O 点，光线折射后进入2n 介质，然后通过B 点。
