相似三角形的基本图形及其应用.docx

(一)相似三角形1、定义：对应角相等，对应边成比例的两个三角形，叫做相似三角形．①当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等，且三条对应边的比相等时，这两个(或几个)三角形叫做相似三角形，即定义中的两个条件，缺一不可；②相似三角形的特征：形状一样，但大小不一定相等；③相似三角形的定义，可得相似三角形的基本性质：对应角相等，对应边成比例．2、相似三角形对应边的比叫做相似比．①全等三角形一定是相似三角形，其相似比k=1．所以全等三角形是相似三角形的特例．其区别在于全等要求对应边相等，而相似要求对应边成比例．②相似比具有顺序性．例如△ABC∽△A′B′C′的对应边的比，即相似比为k，则△A′B′C′∽△ABC的相似比，当它们全等时，才有k=k′=1．③相似比是一个重要概念，后继学习时出现的频率较高，其实质它是将一个图形放大或缩小的倍数，这一点借助相似三角形可观察得出．3、如果两个边数相同的多边形的对应角相等，对应边成比例，那么这两个多边形叫做相似多边形．4、相似三角形的预备定理：平行于三角形的一条边直线，截其它两边所在的直线，截得的三角形与原三角形相似．①定理的基本图形有三种情况，如图其符号语言：∵DE∥BC，∴△ABC∽△ADE；（双A型）②这个定理是用相似三角形定义推导出来的三角形相似的判定定理．它不但本身有着广泛的应用，同时也是证明相似三角形三个判定定理的基础，故把它称为“预备定理”；③有了预备定理后，在解题时不但要想到“见平行，想比例”，还要想到“见平行，想相似”．(二)相似三角形的判定1、相似三角形的判定：判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

可简单说成：两角对应相等，两三角形相似。

例1、已知：如图，∠1=∠2=∠3，求证：△ABC∽△ADE．例2、如图，E 、F 分别是△ABC 的边BC 上的点，DE ∥AB,DF ∥AC , 求证：△ABC ∽△DEF.判定定理2：如果三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

专题12 相似三角形的性质及应用知识网络重难突破知识点一相似三角形的性质①对应角相等，对应边成比例．②周长之比等于相似比；面积之比等于相似比的平方．③对应高线长之比、对应角平分线长之比、对应中线长之比都等于相似比．【典例1】（2020•衢州模拟）如图，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR分别交AC，CD于点P，Q．平行四边形ABCD的面积为6，则图中阴影部分的面积为．【点拨】由四边形ABCD和四边形ACED都是平行四边形，易证得△BCP∽△BER，△ABP∽△CQP∽△DQR，又由点R为DE的中点，可求得各相似三角形的相似比，继而求得答案．【解析】解：∵四边形ABCD和四边形ACED都是平行四边形，∴AD＝BC＝CE，AB∥CD，AC∥DE，∴平行四边形ACED的面积＝平行四边形ABCD的面积＝6，△BCP∽△BER，△ABP∽△CQP∽△DQR，∴△ABC的面积＝△CDE的面积＝3，CP：ER＝BC：BE＝1：2，∵点R为DE的中点，∴CP：DR＝1：2，∴CP：AC＝CP：DE＝1：4，∵S△ABC＝3，∴S△ABP＝S△ABC＝，∵CP：AP＝1：3，∴S△PCQ＝S△ABP＝，∵CP：DR＝1：2，∴S△DQR＝4S△PCQ＝1，∴S阴影＝S△PCQ+S△DQR＝．故答案为：．【点睛】此题考查了平行四边形的性质以及相似三角形的判定与性质．熟记相似三角形的面积比等于相似比的平方是解题的关键．【典例2】（2019秋•河北区期末）如图在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC．（1）求证：△ADE∽△ABC；（2）如AF＝3，AG＝5，求△ADE与△ABC的周长之比．【点拨】（1）由于AG⊥BC，AF⊥DE，所以∠AFE＝∠AGC＝90°，从而可证明∠AED＝∠ACB，进而可证明△ADE∽△ABC；（2）依据△ADE∽△ABC，利用相似三角形的周长之比等于对应高之比，即可得到结论．【解析】解：（1）∵AG⊥BC，AF⊥DE，∴∠AFE＝∠AGC＝90°，∵∠EAF＝∠GAC，∴∠AED＝∠ACB，∵∠EAD＝∠BAC，∴△ADE∽△ABC；（2）由（1）可得△ADE∽△ABC，又∵AG⊥BC于点G，AF⊥DE于点F，∴△ADE与△ABC的周长之比＝＝．【点睛】本题考查相似三角形的判定，解题的关键是熟练运用相似三角形的判定，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．【变式训练】1．（2020春•甘州区校级月考）两个相似三角形面积比是4：9，其中一个三角形的周长为24cm，则另一个三角形的周长是（）cm．A．16 B．16或28 C．36 D．16或36【点拨】根据相似三角形的性质求出相似比，得到周长比，根据题意列出比例式，解答即可．【解析】解：∵两个相似三角形面积比是4：9，∴两个相似三角形相似比是2：3，∴两个相似三角形周长比是2：3，∵一个三角形的周长为24cm，∴另一个三角形的周长是16cm或36cm，故选：D．【点睛】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方是解题的关键．2．（2019秋•慈溪市期末）如图所示，若△ABC∽△DEF，则∠E的度数为（）A．28°B．32°C．42°D．52°【点拨】先求出∠B，根据相似三角形对应角相等就可以得到．【解析】解：∵∠A＝110°，∠C＝28°，∴∠B＝42°，∵△ABC∽△DEF，∴∠B＝∠E．∴∠E＝42°．故选：C．【点睛】本题考查相似三角形的性质的运用，全等三角形的对应角相等，是基础知识要熟练掌握．3．（2019秋•奉化区期末）如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB，若AB＝3BD，则S△ADE：S△EFC的值为（）A．4：1 B．3：2 C．2：1 D．3：1【点拨】由题意可证四边形BDEF是平行四边形，可得BD＝EF，AD＝2EF，通过证明△ADE∽△EFC，可求解．【解析】解：∵AB＝3BD，∴AD＝2BD，∵DE∥BC，EF∥AB，∴四边形BDEF是平行四边形，∴BD＝EF，∴AD＝2EF，∵DE∥BC，EF∥AB，∴∠AED＝∠C，∠FEC＝∠A，∴△ADE∽△EFC，∴S△ADE：S△EFC的＝（）2＝4：1，故选：A．【点睛】本题考查了相似三角形的判定和性质，平行四边形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．4.（2020•下城区模拟）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D，如果＝，AD＝9，那么BC的长是（）A．4 B．6 C．2D．3【点拨】证明△ADC∽△CDB，根据相似三角形的性质求出CD、BD，根据勾股定理求出BC．【解析】解：∵∠ACB＝90°，∴∠ACD+∠BCD＝90°，∵CD⊥AB，∴∠A+∠ACD＝90°，∴∠A＝∠BCD，又∠ADC＝∠CDB，∴△ADC∽△CDB，∴＝，＝，∴＝，即＝，解得，CD＝6，∴＝，解得，BD＝4，∴BC＝＝＝2，故选：C．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．5.（2019•纳溪区模拟）如图，已知矩形ABCD，AB＝6，BC＝10，E，F分别是AB，BC的中点，AF与DE相交于I，与BD相交于H，则四边形BEIH的面积为（）A．6 B．7 C．8 D．9【点拨】延长AF交DC于Q点，由矩形的性质得出CD＝AB＝6，AB∥CD，AD∥BC，得出＝1，△AEI∽△QDE，因此CQ＝AB＝CD＝6，△AEI的面积：△QDI的面积＝1：16，根据三角形的面积公式即可得出结果．【解析】解：延长AF交DC于Q点，如图所示：∵E，F分别是AB，BC的中点，∴AE＝AB＝3，BF＝CF＝BC＝5，∵四边形ABCD是矩形，∴CD＝AB＝6，AB∥CD，AD∥BC，∴＝1，△AEI∽△QDE，∴CQ＝AB＝CD＝6，△AEI的面积：△QDI的面积＝（）2＝，∵AD＝10，∴△AEI中AE边上的高＝2，∴△AEI的面积＝×3×2＝3，∵△ABF的面积＝×5×6＝15，∵AD∥BC，∴△BFH∽△DAH，∴＝＝，∴△BFH的面积＝×2×5＝5，∴四边形BEIH的面积＝△ABF的面积﹣△AEI的面积﹣△BFH的面积＝15﹣3﹣5＝7．故选：B．【点睛】本题考查了矩形的性质、相似三角形的判定与性质、三角形面积的计算；熟练掌握矩形的性质，证明三角形相似是解决问题的关键．6.（2020•杭州）如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB．（1）求证：△BDE∽△EFC．（2）设，①若BC＝12，求线段BE的长；②若△EFC的面积是20，求△ABC的面积．【点拨】（1）由平行线的性质得出∠DEB＝∠FCE，∠DBE＝∠FEC，即可得出结论；（2）①由平行线的性质得出＝＝，即可得出结果；②先求出＝，易证△EFC∽△BAC，由相似三角形的面积比等于相似比的平方即可得出结果．【解析】（1）证明：∵DE∥AC，∴∠DEB＝∠FCE，∵EF∥AB，∴∠DBE＝∠FEC，∴△BDE∽△EFC；（2）解：①∵EF∥AB，∴＝＝，∵EC＝BC﹣BE＝12﹣BE，∴＝，解得：BE＝4；②∵＝，∴＝，∵EF∥AB，∴△EFC∽△BAC，∴＝（）2＝（）2＝，∴S△ABC＝S△EFC＝×20＝45．【点睛】本题考查了相似三角形的判定与性质、平行线的性质等知识；熟练掌握相似三角形的判定与性质是解题的关键．知识点二相似三角形的应用【典例3】（2019秋•解放区校级期中）一块直角三角形木板的面积为1.5m2，一条直角边AB为1.5m，怎样才能把它加工成一个无拼接的面积最大的正方形桌面？甲、乙两位木匠的加工方法如图所示，请你用所学的知识说明哪位木匠的方法符合要求（加工损耗不计，计算结果中的分数可保留）【点拨】结合相似三角形的判定与性质进而得出两个正方形的边长，进而求出面积比较得出答案．【解析】解：由AB＝1.5m，S△ABC＝1.5m2，可得BC＝2m，由图甲，过点B作Rt△ABC斜边AC上的高，BH交DE于P，交AC于H．由AB＝1.5m，BC＝2m，得AC＝＝2.5（m），由AC•BH＝AB•BC可得：BH＝＝1.2（m），设甲设计的桌面的边长为xm，∵DE∥AC，∴Rt△BDE∽Rt△BAC，∴＝，即＝，解得x＝（m），由图乙，若设乙设计的正方形桌面边长为ym，由DE∥AB，得Rt△CDE∽Rt△CBA，∴＝，即＝，解得y＝（m），∵x＝，y＝，∴x＜y，即x2＜y2，∴S正方形甲＜S正方形乙，∴第二个正方形面积大【点睛】此题主要考查了相似三角形的应用，正确表示出正方形的边长是解题关键．【变式训练】1．（2019秋•嘉兴期末）如图，小明在打乒乓球时，为使球恰好能过网（设网高AB＝15cm），且落在对方区域桌子底线C处，已知小明在自己桌子底线上方击球，则他击球点距离桌面的高度DE为（）A．15cm B．20cm C．25cm D．30cm【点拨】证明△CAB∽△CDE，然后利用相似比得到DE的长．【解析】解：∵AB∥DE，∴△CAB∽△CDE，∴＝，而BC＝BE，∴DE＝2AB＝2×15＝30（cm）．故选：D．【点睛】本题考查了相似三角形的应用：利用视点和盲区的知识构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．2．（2019秋•鹿城区月考）如图，AB和CD表示两根直立于地面的柱子，AC和BD表示起固定作用的两根钢筋，AC与BD相交于点M，已知AB＝8m，CD＝12m，则点M离地面的高度MH为（）A．4 m B．m C．5m D．m【点拨】根据已知易得△ABM∽△DCM，可得对应高BH与HD之比，易得MH∥AB，可得△MDH∽△ADB，利用对应边成比例可得比例式，把相关数值代入求解即可．【解析】解：∵AB∥CD，∴△ABM∽△DCM，∴＝＝＝，（相似三角形对应高的比等于相似比），∵MH∥AB，∴△MCH∽△ACB，∴＝＝，∴＝，解得MH＝．故选：B．【点睛】此题主要考查了相似三角形的应用；用到的知识点为：平行于三角形一边的直线与三角形另两边相交，截得的两三角形相似；相似三角形的对应边成比例；对应高的比等于相似比；解决本题的突破点是得到BH与HD的比．3．（2019秋•滨江区期末）如图，小华同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，使斜边DF与地面保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE＝30cm，EF＝15cm，测得边DF离地面的高度AC＝120cm，CD＝600cm，则树AB的高度为420cm．【点拨】利用直角三角形DEF和直角三角形BCD相似求得BC的长，再加上AC的长即可求得树高AB．【解析】解：∵∠DEF＝∠BCD＝90°，∠D＝∠D，∴△DEF∽△DCB，∴BC：EF＝DC：DE，∵DE＝30cm，EF＝15cm，AC＝120cm，CD＝600cm，∴，∴BC＝300cm，∴AB＝AC+BC＝120+300＝420cm，故答案为：420．【点睛】本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．4.（2020•秦皇岛一模）如图所示，AD、BC为两路灯，身高相同的小明、小亮站在两路灯杆之间，两人相距6.5m，小明站在P处，小亮站在Q处，小明在路灯C下的影长为2m，已知小明身高1.8m，路灯BC 高9m．①计算小亮在路灯D下的影长；②计算建筑物AD的高．【点拨】解此题的关键是找到相似三角形，利用相似三角形的性质，相似三角形的对应边成比例求解．【解析】解：①∵EP⊥AB，CB⊥AB，∴∠EP A＝∠CBA＝90°∵∠EAP＝∠CAB，∴△EAP∽△CAB∴∴∴AB＝10BQ＝10﹣2﹣6.5＝1.5；②∵FQ⊥AB，DA⊥AB，∴∠FQB＝∠DAB＝90°∵∠FBQ＝∠DBA，∴△BFQ∽△BDA∴＝∴∴DA＝12．【点睛】本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求出建筑物AB的高与小亮在路灯D下的影长，体现了方程的思想．巩固训练1．（2019秋•连州市期末）两个相似三角形的对应边分别是15cm和23cm，它们的周长相差40cm，则这两个三角形的周长分别是（）A．45cm，85cm B．60cm，100cm C．75cm，115cm D．85cm，125cm【点拨】根据题意两个三角形的相似比是15：23，可得周长比为15：23，计算出周长相差8份及每份的长，可得两三角形周长．【解析】解：根据题意两个三角形的相似比是15：23，周长比就是15：23，大小周长相差8份，所以每份的周长是40÷8＝5cm，所以两个三角形的周长分别为5×15＝75cm，5×23＝115cm．故选：C．【点睛】本题考查对相似三角形性质的理解：（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．2．（2018秋•临安区期末）如图，在△ABC中，BC＝8，高AD＝6，点E，F分别在AB，AC上，点G，H 在BC上，当四边形EFGH是矩形，且EF＝2EH时，则矩形EFGH的周长为（）A．B．C．D．【点拨】通过证明△AEF∽△ABC，可得，可求EH的长，即可求解．【解析】解：如图，记AD与EF的交点为M，∵四边形EFGH是矩形，∴EF∥BC，∴△AEF∽△ABC，∵AM和AD分别是△AEF和△ABC的高，∴∴∴EH＝，∴EF＝，∴矩形EFGH的周长＝2×（+）＝故选：C．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，灵活运用相似三角形的性质是本题的关键．3．（2019秋•庐阳区校级期中）如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE＝1：4，则S△DOE：S△AOC的值为（）A．B．C．D．【点拨】由已知条件易求BE：BC＝1：5；证明△DOE∽△AOC，得到DE：AC的值，由相似三角形的性质即可解决问题．【解析】解：∵S△BDE：S△CDE＝1：4，∴BE：EC＝1：4，∴BE：BC＝1：5，∵DE∥AC，∴△DOE∽△AOC，∴DE：AC＝BE：BC＝1：5，∴S△DOE：S△AOC＝（）2＝，故选：D．【点睛】本题主要考查了相似三角形的判定及其性质的应用问题；熟练掌握相似三角形的判定与性质，证出BE：BC＝1：5是解决问题的关键．4．（2020•上城区一模）如图，△ABC中，D，E两点分别在边AB，BC上，若AD：DB＝CE：EB＝3：4，记△DBE的面积为S1，△ADC的面积为S2，则S1：S2＝16：21．【点拨】过点E、C分别作EF⊥AB于点F，CG⊥AB于点G，根据相似三角形的性质与判定即可求出答案．【解析】解：过点E、C分别作EF⊥AB于点F，CG⊥AB于点G，∴EF∥CG，∴△BEF∽△BCG，∴，∵CE：EB＝3：4，∴，∴，∴＝＝，∴S1：S2＝16：21，故答案为：16：21．【点睛】本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．5．（2019秋•江干区期末）如图，已知▱ABCD中，E是BC的三等分点，连结AE与对角线BD交于点F，则S△BEF：S△ABF：S△ADF：S四边形CDFE＝1：3：9：11．【点拨】由E是BC的三等分点，得到＝，根据平行四边形的性质得到AD∥BC，AD＝BC，根据相似三角形的性质得到＝＝设S△BEF＝k，S△ABF＝3k，S△ADF＝9k，求得S△ABF+S△ADF＝S四边形ABCD＝S△BEF+S四边形CDFE＝12k，得到S四边形CDFE＝12k﹣k＝11k，于是得到结论．【解析】解：∵E是BC的三等分点，∴＝，在▱ABCD中，∵AD∥BC，AD＝BC，∴△ADF∽△EBF，∴＝＝，∴S△BEF：S△ABF：S△ADF＝1：3：9，设S△BEF＝k，S△ABF＝3k，S△ADF＝9k，∴S△ABF+S△ADF＝S四边形ABCD＝S△BEF+S四边形CDFE＝12k，∴四边形CDFE＝12k﹣k＝11k，∴S△BEF：S△ABF：S△ADF：S四边形CDFE＝1：3：9：11，故答案为：1：3：9：11．【点睛】本题考查了平行四边形的性质、相似三角形的判定与性质以及面积的计算方法；熟练掌握平行四边形的性质，证明三角形相似是解决问题的关键．6．（2020•晋安区一模）如图，利用镜子M的反射（入射角等于反射角），来测量旗杆CD的长度，在镜子上作一个标记，观测者AB看着镜子来回移动，直到看到旗杆顶端在镜子中的像与镜子上的标记相重合，若观测者AB的身高为1.6m，量得BM：DM＝2：11，则旗杆的高度为8.8m．【点拨】根据题意抽象出相似三角形，然后利用相似三角形的对应边的比相等列式计算即可．【解析】解：根据题意得：△ABM∽△CDM，∴AB：CD＝BM：DM，∵AB＝1.6m，BM：DM＝2：11，∴1.6：CD＝2：11，解得：CD＝8.8m，故答案为：8.8．【点睛】本题考查了相似三角形的知识，解题的关键是根据实际问题抽象出相似三角形，难度不大．7．（2019秋•竞秀区期末）如图，路灯距地面的高度PO＝8米，身高1.6米的小明在点A处测量发现，他的影长AM＝2.4米，则AO＝9.6米；小明由A处沿AO所在的直线行走8米到点B时，他的影子BN 的长度为0.4米．【点拨】如图，设OA＝x，BN＝y．利用相似三角形的性质构建方程组即可解决问题．【解析】解：如图，设OA＝x，BN＝y．∵EB∥OP∥F A，∴△MAF∽△MOP，△NBE∽△NOP，∴＝，＝，∴＝，＝，解得x＝9.6，y＝0.4，故答案为9.6，0.4．【点睛】本题考查相似三角形的应用，解题的关键是学会利用参数构建方程组解决问题，属于中考常考题型．8．（2019秋•开江县期末）如图，学校操场旁立着一杆路灯（线段OP）．小明拿着一根长2m的竹竿去测量路灯的高度，他走到路灯旁的一个地点A竖起竹竿（线段AE），这时他量了一下竹竿的影长AC正好是1m，他沿着影子的方向走了4m到达点B，又竖起竹竿（线段BF），这时竹竿的影长BD正好是2m，请利用上述条件求出路灯的高度．【点拨】根据相似三角形的性质即可得到结论．【解析】解：由于BF＝DB＝2m，即∠D＝45°，∴DP＝OP＝灯高．在△CEA与△COP中，∵AE⊥CP，OP⊥CP，∴AE∥OP．∴△CEA∽△COP，∴．设AP＝xm，OP＝hm，则，①，DP＝OP＝2+4+x＝h，②联立①②两式，解得x＝4，h＝10．∴路灯有10m高．【点睛】本题考查了相似三角形的性质，熟练掌握相似三角形的性质是解题的关键．9．（2019秋•余杭区期末）如图，在△ABC中，点D，E分别在边AC，AB上且AE•AB＝AD•AC，连结DE，BD．（1）求证：△ADE∽△ABC．（2）若点E为AB中点，AD：AE＝6：5，△ABC的面积为50，求△BCD的面积．【点拨】（1）由已知得出AE：AC＝AD：AB，由∠A＝∠A，即可得出：△ADE∽△ABC．（2）设AD＝6x，则AE＝5x，AB＝10x，由已知求出AC＝＝x，得出CD＝AC﹣AD＝x，得出＝，由三角形面积关系即可得出答案．【解析】（1）证明：∵AE•AB＝AD•AC，∴AE：AC＝AD：AB，∵∠A＝∠A，∴△ADE∽△ABC．（2）解：∵点E为AB中点，∴AE＝BE，∵AD：AE＝6：5，∴设AD＝6x，则AE＝5x，AB＝10x，∵AE•AB＝AD•AC，∴AC＝＝＝x，∴CD＝AC﹣AD＝x，∴＝，∵△ABC的面积为50，∴△BCD的面积＝×50＝14．【点睛】本题考查了相似三角形的判定与性质、三角形面积关系等知识；熟练掌握相似三角形的判定与性质是解题的关键．10．（2018秋•江干区期末）如图，在菱形ABCD中，点E在BC边上（不与点B、C重合），连接AE、BD 交于点G．（1）若AG＝BG，AB＝4，BD＝6，求线段DG的长；（2）设BC＝kBE，△BGE的面积为S，△AGD和四边形CDGE的面积分别为S1和S2，把S1和S2分别用k、S的代数式表示；（3）求的最大值．【点拨】（1）证明△BAG∽△BDA，利用相似比可计算出BG＝，从而得到DG的长；（2）先证明△ADG∽△EBG，利用相似三角形的性质得＝（）2＝k2，＝＝k，所以S1＝k2S，根据三角形面积公式得到S△ABG＝，再利用菱形的性质得到S2＝S1+﹣S＝k2S+kS﹣S＝（k2+k﹣1）S；（3）由于＝＝1+﹣，然后根据二次函数的性质解决问题．【解析】解：（1）∵AG＝BG，∴∠BAG＝∠ABG，∵四边形ABCD为菱形，∴AB＝AD，∴∠ABD＝∠ADB，∴∠BAG＝∠ADB，∴△BAG∽△BDA，∴＝，即＝，∴BG＝，∴DG＝BD﹣BG＝6﹣＝；（2）∵四边形ABCD为菱形，∴BC＝AD＝kBE，AD∥BC，∵AD∥BE，∴∠DAE＝∠BEA，∠ADG＝∠BEG∴△ADG∽△EBG，∴＝（）2＝k2，＝＝k，∴S1＝k2S，∵＝＝k，∴S△ABG＝，∵△ABD的面积＝△BDC的面积，∴S2＝S1+﹣S＝k2S+kS﹣S＝（k2+k﹣1）S；（3）∵＝＝1+﹣＝﹣（﹣）2+，∴的最大值为．【点睛】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．注意相似三角形面积的比等于相似比的平方．也考查了菱形的性质．。

相似三角形知识点与经典题型知识点 1 有关相似形的概念(1) 形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形 .(2) 如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形．相似多边形对应边长度的比叫做相似比( 相似系数 ) ．知识点 2 比例线段的相关概念（ 1）如果选用同一单位量得两条线段 a,b 的长度分别为 m, n ，那么就说这两条线段的比是amb n ，或写成 a : bm : n ．注：在求线段比时，线段单位要统一。

（ 2）在四条线段 a, b, c, d 中，如果 a 和 b 的比等于 c 和d 的比，那么这四条线段a,b,c, d 叫做成比例线段，简称比例线段． 注：①比例线段是有顺序的， 如果说 a 是 b, c, d 的第四比例项， 那么应得比例式为：bd ．② a ccac ： d)中，a 、d 叫比例外项， b 、c 叫比例内项 , a 、c 叫比例前项， b 、d 叫比例后在比例式(a ： bbdb=c ，即 a ：b b ：d 那么 b 叫做 a 、 d 的比例中项， 此时有 b 2项， d 叫第四比例项，如果 ad 。

（ 3）黄金分割：把线段AB 分成两条线段 AC , BC ( AC BC ) ，且使 AC 是 AB 和 BC 的比例中项，即AC 2 AB BC ，叫做把线段 AB 黄金分割，点 C 叫做线段 AB 的黄金分割点，其中AC5 1AB ≈20.618 AB ．即ACBC 5 1 简记为： 长＝ 短＝5 1ABAC2全 长 2注：黄金三角形：顶角是360 的等腰三角形。

黄金矩形：宽与长的比等于黄金数的矩形知识点 3 比例的性质（ 注意性质立的条件：分母不能为0）（ 1） 基本性质：① a : b c : d adbc ；② a : b b : c b 2a c ． ad bc ，除注：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如了可化为 a : b c : d ，还可化为 a : c b : d ， c : d a : b ， b : d a : c ， b : ad : c ， c : a d : b ，d : c b : a ， d : b c : a ．a b，交换内项)c d (（ 2） 更比性质 ( 交换比例的内项或外项) ：ac d c ，交换外项( )b db ad b．同时交换内外项)ca (（ 3）反比性质 ( 把比的前项、后项交换) ：ac bd ．b da c（ 4）合、分比性质：a c abcd ．bdbd注：实际上，比例的合比性质可扩展为：比例式中等号左右两个比的前项，后项之间b ad c发生同样和差变化比例仍成立．如：a cac 等等．b da b c da bc d（ 5）等比性质：如果 ac e m(b d fn 0) ，那么 acem a ．bd fnb d f nb注：①此性质的证明运用了“设 k 法”（即引入新的参数 k ）这样可以减少未知数的个数，这种方法是有关比例计算变形中一种常用方法．②应用等比性质时，要考虑到分母是否为零．③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数，再利用等比性质也成立．如：a c e a 2c 3e a 2c 3e a；其中 b 2d 3 f 0．b d f b 2d 3 f b 2d 3 fb知识点 4比例线段的有关定理1. 三角形中平行线分线段成比例定理: 平行于三角形一边的直线截其它两边( 或两边的延长线 ) 所得的对应线段成比例 .A由 DE ∥ BC 可得：注：AD AE 或 BD EC 或 AD AE DB EC AD EA AB ACD EB C①重要结论：平行于三角形的一边, 并且和其它两边相交的直线, 所截的三角形的三边 与原三角形三边 对应成比．．．．．． ．．．．．．例 .②三角形中平行线分线段成比例定理的逆定理： 如果一条直线截三角形的两边( 或两边的延长线 ) 所得的对应线段成比例 . 那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法 , 即：利用比例式证平行线 .③平行线的应用：在证明有关比例线段时，辅助线往往做平行线, 但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比 .2. 平行线分线段成比例定理: 三条平行线截两条直线 , 所截得的对应线段成比例 .A D 已知 AD ∥ BE ∥CF,BE可得ABDE 或 AB DE 或 BC EF 或 BC EF 或 AB BC 等. CFBCEF AC DF AB DE AC DF DE EF注：平行线分线段成比例定理的推论：平行线等分线段定理： 两条直线被三条平行线所截， 如果在其中一条上截得的线段相等， 那么在另一条上截得的线段也相等。

课件相似三角形的应用(多场景)课件：相似三角形的应用一、引言相似三角形是几何学中的重要概念，广泛应用于日常生活和工程实践。

相似三角形的应用不仅体现在数学领域，还涉及物理学、建筑学、地理学等多个领域。

本课件旨在介绍相似三角形的基本概念及其在不同领域的应用，帮助大家更好地理解相似三角形的实用价值。

二、相似三角形的基本概念1.相似三角形的定义：如果两个三角形的对应角相等，且对应边成比例，则这两个三角形相似。

2.相似三角形的性质：相似三角形的对应角相等，对应边成比例，对应高的比、对应中线的比、对应角平分线的比都相等。

3.判定相似三角形的方法：AA（角角）相似定理、SAS（边角边）相似定理、SSS（边边边）相似定理。

三、相似三角形在数学领域的应用1.解直角三角形：利用相似三角形的性质，可以求解直角三角形中的未知边长和角度。

2.求解相似多边形：在解决多边形问题时，相似三角形的应用可以帮助我们求解多边形的边长、面积等几何量。

3.解析几何：在解析几何中，相似三角形的应用可以帮助我们求解直线、圆等几何图形的方程。

四、相似三角形在物理学领域的应用1.测量不规则物体的体积：利用相似三角形，可以求解不规则物体的体积，如测量岩石、木材等。

2.测量距离：在物理学实验中，相似三角形的应用可以帮助我们测量不易直接测量的距离，如测量地球到月球之间的距离。

3.解析力学：在解析力学中，相似三角形的应用可以帮助我们求解力的分解、力的合成等问题。

五、相似三角形在建筑学领域的应用1.设计建筑结构：相似三角形的应用可以帮助建筑师设计出稳定、美观的建筑结构。

2.测量建筑物的尺寸：在建筑物的施工过程中，相似三角形的应用可以帮助测量建筑物的尺寸，确保施工质量。

3.求解建筑物的高度：利用相似三角形，可以求解建筑物的高度，如测量塔的高度、建筑物之间的距离等。

六、相似三角形在地理学领域的应用1.测量地球表面距离：相似三角形的应用可以帮助测量地球表面两点之间的距离，如测量城市之间的距离。

4.5相似三角形的性质及应用一、相似三角形的性质1．相似三角形的对应角相等，对应边的比相等. 2. 相似三角形中的重要线段的比等于相似比.相似三角形对应高，对应中线，对应角平分线的比都等于相似比. 要点：要特别注意“对应”两个字，在应用时，要注意找准对应线段. 3. 相似三角形周长的比等于相似比∽，则由比例性质可得：4. 相似三角形面积的比等于相似比的平方∽，则分别作出与的高和，则21122=1122ABCA B C BC AD k B C k A D S k S B C A D B C A D '''''''⋅⋅⋅⋅=='''''''''⋅⋅△△要点：相似三角形的性质是通过比例线段的性质推证出来的. 二、三角形的重心三角形三条中线的交点叫做三角形的重心，三角形的重心分每一条中线成1:2的两条线段.OEFDABC即12OD OE OF OA OB OC === . 要点：H OEFDAB C过点E 作EH ∥BC 交AD 于H ，根据三角形的中位线平行于第三边并且等于第三边的一半可得CD=2EH ，从而得到BD=2EH ，再根据△BDO 和△EHO 相似，利用相似三角形对应边成比例列出比例式计算即可得证1=2OE HE OB BD ，同理其他比例也可以得到． 三、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度，通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点：测量旗杆的高度的几种方法：平面镜测量法 影子测量法 手臂测量法 标杆测量法2.测量距离测量不能直接到达的两点间的距离，常构造如下两种相似三角形求解。

1．如甲图所示，通常可先测量图中的线段DC 、BD 、CE 的距离（长度），根据相似三角形的性质，求出AB 的长.2．如乙图所示，可先测AC 、DC 及DE 的长，再根据相似三角形的性质计算AB 的长.要点：1．比例尺：表示图上距离比实地距离缩小的程度，比例尺= 图上距离/ 实际距离;2．太阳离我们非常遥远，因此可以把太阳光近似看成平行光线．在同一时刻，两物体影子之比等于其对应高的比;3．视点：观察事物的着眼点（一般指观察者眼睛的位置）; 4. 仰（俯）角：观察者向上（下）看时，视线与水平方向的夹角． 一、单选题1．两三角形的相似比是2：3，则其对应角的角平分线之比是（ ） A ．2:3 B ．2：3 C ．4：9 D ．8：27 【解答】B【提示】根据相似三角形对应角平分线的比等于相似比解答即可． 【详解】解：∵两三角形的相似比是2：3， ∴相似三角形对应角平分线的比是2：3，故选：B ．【点睛】本题考查了相似三角形的性质，主要利用了相似三角形对应角平分线的比，对应高的比，对应中线的比都等于相似比的性质．2．已知ABC DEF ∽△△，ABC 与DEF 的面积之比为1：2，若BC 边上的中线长为1，则EF 边上的中线长是（ ） A ．2 B ．2 C ．3D ．4【解答】A【提示】由ABC DEF ∽△△，ABC 与DEF 的面积之比为1：2可知：相似比为1:2，则对应中线的比为1:2，即可求出答案．【详解】∵ABC DEF ∽△△，ABC 与DEF 的面积之比为1：2 ∴相似比为1:2 ∴其对应中线的比为1:2 ∵BC 边上的中线长为1 ∴EF 边上的中线长是2 故选：A【点睛】本题主要考查了相似三角形的相似比的相关知识点，熟练掌握相似三角形面积比、相似比、对应边的高线、中线的比的关系是解题的关键，属于基础知识题．3．如图点D 、E 分别在△ABC 的两边BA 、CA 的延长线上，下列条件能判定ED ∥BC 的是（ ）．A ．AD DEAB BC =； B ．AD AE AC AB =；C ．AD AB DE BC ⋅=⋅； D ．AD AC AB AE ⋅=⋅． 【解答】D【提示】根据选项选出能推出ADE ABC ∆∆∽，推出D B ∠=∠或E C ∠=∠的即可判断． 【详解】解：A 、∵AD DEAB BC =，EAD BAC ∠=∠，不符合两边对应成比例及夹角相等的相似三角形判定定理. 无法判断ADE ∆与ABC ∆相似，即不能推出//DE BC ，故本选项错误；B 、AD AE AC AB =EAD BAC ∠=∠， ADE ACB ∴∆∆∽，E B ∴∠=∠，D C ∠=∠，即不能推出//DE BC ，故本选项错误；C 、由AD AB DE BC ⋅=⋅可知AB DEBC AD =，不能推出DAE BAC ∆∆∽，即不能推出D B ∠=∠，即不能推出两直线平行，故本选项错误；D 、∵AD AC AB AE ⋅=⋅，AD AEAB AC ∴=，EAD BAC ∠=∠， DAE BAC ∴∆∆∽，D B ∴∠=∠，//DE BC ∴，故本选项正确；故选：D ．【点睛】本题考查了相似三角形的性质和判定和平行线的判定的应用，主要考查学生的推理和辨析能力，注意：有两组对应边的比相等，且这两边的夹角相等的两三角形相似． 4．已知ABC 与DEF 相似，且A D ∠=∠，那么下列结论中，一定成立的是（ ） A ．B E ∠=∠ B ．AB ACDE DF =C ．相似比为AB DED ．相似比为BCEF【解答】D【提示】根据相似三角形的性质对不同的对应角和对应边进行分类讨论．【详解】解：∵B 可以与E 对应，也可以与F 对应，∴∠B=∠E 或∠B=∠F ，A 不一定成立； 同上，AB 可以与DE 对应，也可以与DF 对应，∴AB AC DE DF =或AB ACDF DE =，B 不一定成立；同上，AB 可以与DE 对应，也可以与DF 对应，∴相似比可能是AB DE ，也可能是ABDF ，C 不一定成立；∵∠A=∠D ，即∠A 与∠D 是对应角，∴它们的对边一定是对应比，即BC 与EF 是对应比，∴相似比为BCEF ，∴D 一定成立， 故选D ．【点睛】本题考查相似三角形的性质，注意相似三角形的性质是针对对应角和对应边而言的． 5．如图，小明站在 C 处看甲、乙两楼楼顶上的点 A 和点 E ．C ，E ，A 三点在同一直线上，B ，C 相距 20 米，D ，C 相距 40 米，乙楼的高 BE 为 15 米，小明的身高忽略不计，则甲楼的高 AD 为 （ ）A ．40 米B ．20 米C ．15 米D ．30 米【解答】D【提示】证明ADC EBC ∽△△，利用相似三角形的性质解答即可． 【详解】解：由题意可知：90ADC ∠=︒，90EBC ∠=︒，C ∠是公共角，∴ADC EBC ∽△△， ∴AD DCEB BC =， ∵20m BC =，40m DC =，15m BE =， ∴40=15=30m 20DC AD EB BC =⨯⨯．故选：D【点睛】本题考查相似三角形的判定及性质，解题的关键是熟练掌握相似三角形的判定及性质． 6．如图，在Rt △ABC 中，90ACB ∠=，CD AB ⊥垂足为D ，那么下列结论错误的是（ ）A ．22AC BD BC AD ⋅=⋅B ．22BC BD CD AB ⋅=⋅C ．AD BC AC CD ⋅=⋅ D ．CD BC AC BD ⋅=⋅ 【解答】B【提示】根据直角三角形的性质与相似三角形的判定可知△ADC ∽△CDB ∽△ACB ，利用相似三角形的对应线段成比例即可求解. 【详解】∵∠ACB=90°，CD ⊥AB ， ∴△ADC ∽△CDB ∽△ACB ∴AC2=AD·AB ，BC2=BD·AB ，故22AC BD BC AD ⋅=⋅，A 正确，B 错误；∵△ADC ∽△CDB∴AD AC CDCD BC BD == ∴AD BC AC CD ⋅=⋅，CD BC AC BD ⋅=⋅,C,D 选项正确； 故选B.【点睛】此题主要考查相似三角形的判定与性质，解题的关键是熟知直角三角形的性质及相似三角形的判定.7．如图，E ，F 是平行四边形ABCD 对角线AC 上两点，AE=CF=14AC ．连接DE ，DF 并延长，分别交AB ，BC 于点G ，H ，连接GH ，则ADG BGHS S △△的值为（ ）A ．12B ．23C ．34D ．1【解答】C【提示】首先证明AG ：AB=CH ：BC=1：3，推出GH ∥AC ，推出△BGH ∽△BAC ，可得223924ADC BAC BGHBGHS S BA SSBG （）（）====,13ADG ADCSS=，由此即可解决问题．【详解】∵四边形ABCD 是平行四边形 ∴AD=BC ，DC=AB ， ∵AC=CA ， ∴△ADC ≌△CBA ， ∴S △ADC=S △ABC ，∵AE=CF=14AC ，AG ∥CD ，CH ∥AD ，∴AG ：DC=AE ：CE=1：3，CH ：AD=CF ：AF=1：3， ∴AG ：AB=CH ：BC=1：3， ∴GH ∥AC ， ∴△BGH ∽△BAC ， ∴223924ADC BAC BGHBGHS S BA S SBG （）（）====，∵13ADG ADCS S=，∴913434ADG BGHS S=⨯=.故选C ．【点睛】本题考查平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等高模型等知识，解题的关键是灵活运用所学知识解决问题，属于中考选择题中的压轴题．8．如图，在正方形ABCD 中，ABP 是等边三角形，AP 、BP 的延长线分别交边CD 于点E 、F ，联结AC 、CP 、AC 与BF 相交于点H ，下列结论中错误的是（ ）A ．AE=2DEB ．CFP APHC ．CFP APCD ．2CP PH PB =⋅【解答】C【提示】A.利用直角三角形30度角的性质即可解决问题． B.根据两角相等两个三角形相似即可判断．C.通过计算证明∠DPB≠∠DPF ，即可判断．D.利用相似三角形的性质即可证明． 【详解】解：∵四边形ABCD 是正方形， ∴∠D=∠DAB=90°， ∵△ABP 是等边三角形， ∴∠PAB=∠PBA=∠APB=60°， ∴∠DAE=30°， ∴AE=2DE ，故A 正确; ∵AB ∥CD ，∴∠CFP=∠ABP=∠APH=60°，∵∠PHA=∠PBA+∠BAH=60°+45°=105°， 又∵BC=BP ，∠PBC=30°， ∴∠BPC=∠BCP=75°， ∴∠CPF=105°，∴∠PHA=∠CPF ，又易得∠APB=∠CFP=60°， ∴△CFP ∽△APH ，故B 正确; ∵∠CPB=60°+75°=135°≠∠DPF ， ∴△PFC 与△PCA 不相似，故C 错误; ∵∠PCH=∠PCB-∠BCH=75°-45°=30°， ∴∠PCH=∠PBC ， ∵∠CPH=∠BPC ， ∴△PCH ∽△PBC ，∴PC PHPB PC =,∴PC2=PH•PB ，故D 正确， 故选：C ．【点睛】本题考查相似三角形的判定和性质，等边三角形的性质，正方形的性质，直角三角形30度角的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．9．如图所示，D 、E 分别是ABC ∆的边AB 、BC 上的点，且//DE AC ，AE 、CD 相交于点O ．若45::2DOE COA S S ∆∆=，则BDES ∆与CDE S ∆的比是（ ）A ．1：2B ．1： 3C ．2：3D ．2：5 【解答】C【提示】利用相似三角形的性质解决问题即可． 【详解】解：∵//DE AC ， ∴DEO CAO ∆∆∽， ∵45::2DOE COA S S ∆∆=，∴2425DE AC ⎛⎫=⎪⎝⎭，∴25DE AC =， ∵//DE AC ， ∴25BE DE BC AC ==， ∴23BE EC =，∴BDES ∆与CDE S ∆的比2:3=，故选：C ．【点睛】本题主要考查的是相似三角形的性质和判定，熟练掌握相似三角形的性质和判定定理是解题的关键．10．如图，正方形ABCD 和正方形CGFE 的顶点,,C D E 在同一条直线上，顶点, ,B C G 在同一条直线上．O 是EG 的中点，EGC ∠的平分线GH 过点D ，交BE 于点H ，连接FH 交EG 于点M ，连接OH 交EC 于点N ．则BCCG 的值为（ ）A ．31-B ．3C ．21-D ．2【解答】C【详解】∵四边形ABCD 和四边形CGFE 是正方形，,,BC DC CE CG BCE DCG ∴==∠=∠．在BCE和DCG △中，,,(),,BC DC BCE DCG BCE DCG SAS BEC BGH CE CG =⎧⎪∠=∠∴∴∠=∠⎨⎪=⎩≌．90BGH CDG ∠+∠=︒，,90CDG HDE BEC HDE ∠=∠∴∠+∠=︒．GH BE ∴⊥．GH 平分,EGC BGH EGH ∠∴∠=∠．()BGH EGH ASA ∴≌．BH EH ∴=．又O 是EG 的中点，//HO BG ∴．D C DHN G ∴∽△△．DN HN DC CG ∴=．设HN a =，正方形ECGF 的边长是2b ，则2BC a =，22,,22b a aCD a NC b a b -==∴=，即2220a ab b +-=，解得(12)a b =-+或(12)a b =--（舍去），则221,212a BCb CG =-∴=-．二、填空题11．若两个相似三角形的面积比是9：25，则对应边上的中线的比为 _________． 【解答】3：5【提示】根据相似三角形的性质：相似三角形对应边上的中线之比等于相似比即可得出答案． 【详解】∵两个相似三角形的面积比是9：25 ∴两个相似三角形的相似比是3：5 ∴对应边上的中线的比为3：5 故答案为：3：5．【点睛】本题主要考查相似三角形的性质，掌握相似三角形的性质是解题的关键． 12．如图，△ABC ∽△CBD ，AB=9，BD=25，则BC=______．【解答】15【提示】根据相似三角形的性质列出比例式，代入计算即可求解． 【详解】解：∵△ABC ∽△CBD ，∴AB CBCB BD =，即2BC AB BD =⨯， AB=9，BD=25，2292522515BC AB BD ∴=⨯=⨯==，15BC =∴， 故答案为：15【点睛】本题考查了相似三角形的性质，根据相似三角形的性质列出比例式是解题的关键． 13．一个三角形三边长度之比为2：5：6，另一个与它相似的三角形最长边为24，则三角形的最短边为_________． 【解答】8【提示】首先设与它相似的三角形的最短边的长为x ，然后根据相似三角形的对应边成比例，即可得方程，解此方程即可求得答案．【详解】解：设与它相似的三角形的最短边的长为x ，则 2624x =，∴8x =；∴三角形的最短边为8． 故答案为：8．【点睛】此题考查了相似三角形的性质．此题比较简单，注意掌握相似三角形的对应边成比例定理的应用．14．如图，在矩形ABCD 中，E 是BC 的中点，连接AE ，过点E 作EF AE ⊥交DC 于点F ．若4AB =，6BC =，则DF 的长为______．【解答】74【提示】结合矩形的性质证明BAECEF ∆∆可求得CF 的长，再利用DF CD DF =-可求解．【详解】解：四边形ABCD 为矩形，90B C ∴∠=∠=︒，4CD AB ==，90BAE AEB ∴∠+∠=︒，EF AE⊥，90AEF∴∠=︒，90AEB CEF∴∠+∠=︒，BAE CEF∴∠=∠，BAE CEF∴∆∆，::AB CE BE CF∴=，E是BC的中点，6BC=，3BE CE∴==，4AB=，4:33:CF∴=，解得94CF=，97444DF CD DF∴=-=-=．故选：7 4．【点睛】本题主要考查矩形的性质，相似三角形的判定与性质，证明BAE CEF∆∆是解题的关键．15．用杠杆撬石头的示意图如图所示，P是支点，当用力压杠杆的A端时，杠杆绕P点转动，另一端B向上翘起，石头就被撬动．现有一块石头要使其滚动，杠杆的B端必须向上翘起8cm，已知杠杆的动力臂AP与阻力臂BP之比为4：1，要使这块石头滚动，至少要将杠杆的A端向下压_____cm．【解答】32【提示】首先根据题意画出图形，然后根据△APM∽△BPN有AP AMBP BN=，然后再利用动力臂AP与阻力臂BP之比为4：1和8BN≥即可求出AM的最小值．【详解】解：如图：AM、BN都与水平线垂直，即AM∥BN；∴△APM∽△BPN；∴APBP＝AMBN，∵杠杆的动力臂AP与阻力臂BP之比为4：1，∴AMBN＝41，即AM＝4BN；∴当BN≥8cm时，AM≥32cm；故要使这块石头滚动，至少要将杠杆的端点A 向下压32cm ． 故答案为：32．【点睛】本题主要考查相似三角形的判定及性质的应用，掌握相似三角形的判定及性质是解题的关键． 16．如图，已知,20,60AB BC ACBAD DAE AD DE AE ︒︒==∠=∠=，则DAC ∠的度数为_________．【解答】40°【提示】由AB BC ACAD DE AE ==可判定△ABC ∽△ADE ，得到∠BAC=∠DAE ，再根据20BAD ︒∠=，60DAE ︒∠=，可得出∠DAC 的度数.【详解】解：∵AB BC ACAD DE AE ==， ∴~ABC ADE ， ∴60BAC DAE ︒∠=∠=， 又∵20BAD ︒∠=， ∴40DAC ︒∠=． 故答案为：40°.【点睛】本题考查了相似三角形的判定和性质，解题的关键是能根据AB BC ACAD DE AE ==判定出△ABC ∽△ADE.17．如图，已知在ABC 中，90C ∠=︒，10AB =，1cot 2B =，正方形DEFG 的顶点G 、F 分别在边AC 、BC 上，点D 、E 在斜边AB 上，那么正方形DEFG 的边长为_____．【解答】207【提示】作CM ⊥AB 于M ，交GF 于N ，由勾股定理可得出AB ，由面积法求出CM ，证明△CGF ∽△CAB ，再根据对应边成比例，即可得出答案． 【详解】作CM ⊥AB 于M ，交GF 于N ，如图所示： ∵Rt △ABC 中，∠C ＝90°，AB ＝10，1cot B 2=，∴设BC ＝k ，则AC ＝2k ，AB2＝AC2＋BC2，即：102＝（2k ）2＋k2，解得：k ＝25， ∴BC ＝25，AC ＝45， ∴CM ＝AC BC AB ⋅＝452510⨯＝4，∵正方形DEFG 内接于△ABC ， ∴GF ＝EF ＝MN ，GF ∥AB ， ∴△CGF ∽△CAB ，∴CN GF =CM AB ，即4EF EF410-=， 解得：EF ＝207；故答案为：207．【点睛】本题考查的是相似三角形的判定和性质、正方形的性质、勾股定理等知识；正确作出辅助线、灵活运用相似三角形的判定定理和性质定理是解题的关键．18．如图，在ABC 中，90ACB ∠=︒，AC BC =，点E 是边AC 上一点，以BE 为斜边往BC 侧作等腰Rt BEF △，连接,CF AF ，若6AB =，四边形ABFC 的面积为12，则AE =_________，AF =_________．【解答】 234【提示】如图，过点E 作EH AB ⊥于H ，过点F 作FQ AC ⊥，交AC 的延长线于Q ，由面积和差关系可求3BCF S ∆=，通过证明ABE CBF ∆∆∽，可得2()ABE BCF S AB S BC∆∆=，可求2EH =，由勾股定理可求AE ，BE ，EF 的长，通过证明BEH EFQ ∆∆∽，可得2BE EH BH EF QF EQ ===，可求22EQ =，2QF =，由勾股定理可求解．【详解】解：如图，过点E 作EH AB ⊥于H ，过点F 作FQ AC ⊥，交AC 的延长线于Q ，90ACB ∠=︒，AC BC =，2AB BC ∴，=6AB ，32AC BC ∴==四边形ABFC 的面积为12，12ABC BCF S S ∆∆∴+=， 3BCF S ∆∴=，等腰Rt BEF ∆，2BE BF ∴，45EBF∠=︒，=45ABC ∠︒，ABE CBF ∴∠=∠，2AB BE BC FB == ABE CBF ∴∆∆∽，∴2()ABE BCF S AB S BC ∆∆=， 326ABE S ∆∴=⨯=，∴162AB EH ⨯=，2EH ∴=，45CAB ∠=︒，EH AB ⊥，45CAB AEH ∴∠=∠=︒，2AH EH ∴==，222AE EH ==，4BH ∴=，2CE =，2221825BE CE BC ∴=+=+=，10EF ∴=，180AEH BEH FEB QEF ∠+∠+∠+∠=︒， 90BEH FEQ ∴∠+∠=︒，且90BEH EBH ∠+∠=︒EBH QEF ∴∠=∠，且90Q BHE ∠=∠=︒，BEH EFQ ∴∆∆∽， ∴2BE EH BHEF QF EQ ===， 22EQ ∴=，2QF =， 42AQ ∴=，2232234AF AQ QF ∴=+=+=，故答案为：22，34．【点睛】本题考查了相似三角形的判定和性质，等腰直角三角形的性质，勾股定理等知识，利用相似三角形的性质求出EH 的长是本题的关键．三、解答题19．如图，在ABP 中，C ，D 分别是,AP BP 上的点．若4,5,6,3CD CP DP AC BD =====．(1)求证：ABP DCP ∽△△； (2)求AB 的长． 【解答】(1)见解析(2)AB＝8【提示】（1）△ABP与△DCP有公共角，分别计算PDPC与APBP的值，得到PD PCPA PB=，根据相似三角形的判定定理得出结论；（2）运用相似三角形的性质计算即可．（1）证明：∵CD＝CP＝4，DP＝5，AC＝6，BD＝3，∴AP＝AC+CP＝6+4＝10，BP＝BD+DP＝3+5＝8，∴54PDPC=，10584APBP==，∴PD APPC BP=，即PD PCPA PB=，∵∠DPC＝∠APB，∴△ABP∽△DCP；（2）解：∵△ABP∽△DCP，∴AB PBCD PC=，即844AB=，∴AB＝8．【点睛】本题考查了相似三角形的判定与性质，属于基础题．解决问题的关键是掌握：有两边对应成比例且夹角相等的两个三角形相似．20．如图，在矩形ABCD中，AB：BC＝1：2，点E在AD上，BE与对角线AC交于点F．(1)求证：△AEF∽△CBF；(2)若BE⊥AC，求AE：ED．【解答】(1)见解析(2)1：3【提示】（1）根据矩形的性质得到AD∥BC，然后根据相似三角形的判断方法可判断△AEF∽△CBF；（2）设AB=x，则BC=2x，利用矩形的性质得到AD=BC=2x，∠BAD=∠ABC=90°，接着证明△ABE∽△BCA，利用相似比得到AE=12x，则DE=32x，从而可计算出AE：DE．（1）解：证明：∵四边形ABCD为矩形，∴AD∥BC，∴△AEF∽△CBF；（2）设AB=x，则BC=2x，∵四边形ABCD为矩形，∴AD=BC=2x，∠BAD=∠ABC=90°，∵BE⊥AC，∴∠AFB=90°，∵∠ABF+∠BAF=90°，∠BAC+∠ACB=90°，∴∠ABF=∠ACB，∵∠BAE=∠ABC，∠ABE=∠BCA，∴△ABE∽△BCA，∴AE ABAB BC=，即2AE xx x=，∴AE=12x，∴DE=AD-AE=32x，∴AE：DE=13:22x x=1：3．【点睛】本题考查了三角形相似的判定与性质，应注意利用图形中已有的公共角、公共边等条件，同时利用相似三角形的性质进行几何计算．也考查了矩形的性质．21．如图，为了测量平静的河面的宽度EP，在离河岸D点3.2米远的B点，立一根长为1.6米的标杆AB，在河对岸的岸边有一根长为4.5米的电线杆MF，电线杆的顶端M在河里的倒影为点N，即PM PN=，两岸均高出水平面0.75米，即0.75DE FP==米，经测量此时A、D、N三点在同一直线上，并且点M、F、P、N N共线，点B、D、F共线，若AB、DE、MF均垂直与河面EP，求河宽EP是多少米？【解答】河宽为12米【提示】连接DF ，根据题意可得出四边形DEPF 为矩形，由ADB NDF ∽△△可求得DF ，便可解决问题．【详解】解：如图，连接DF ，∵点B 、D 、F 共线，DE 、MF 均垂直与河面EP ，且0.75DE FP ==， 4.5MF =， ∴四边形DEPF 为矩形， ∴DF EP =，∴ 4.50.75 5.25PN FM FP =+=+=， ∴ 5.250.756FN PN FP =+=+=， ∵AB 、DE 、MF 均垂直与河面EP ， ∴90ABD NFD ∠=∠=︒， ∵ADB NDF ∠=∠， ∴ADB NDF ∽△△； ∴AB NFBD DF =， ∵ 1.6AB =， 3.2BD =， ∴1.663.2DF =，∴12DF =， ∴12EP =（米）． 答：河宽EP 是12米．【点睛】本题主要考查了相似三角形的性质与判定，矩形的判定和性质等知识．关键是构造和证明三角形相似．22．如图，已知AD ，BC 相交于点E ，且△AEB ∽△DEC ，CD ＝2AB ，延长DC 到点G ，使CG ＝12CD ，连接AG ．(1)求证：四边形ABCG 是平行四边形；(2)若∠GAD ＝90°，AE ＝2，CG ＝3，求AG 的长． 【解答】(1)证明见解析； (2)35AG =【提示】（1）根据相似三角形的性质可得AB ∥CD ，再由CD ＝2AB ，CG ＝12CD ，可得AB ＝CG ，即可证明；（2）由平行四边形的性质可得AG ∥BC ，可得∠AEB ＝90°，再由CG ＝3可得AB ＝3，利用勾股定理可得BE ，再由相似三角形的性质可得CE ，从而得出BC ，即可求解． （1）证明：∵△AEB ∽△DEC ， ∴∠B ＝∠BCD ， ∴AB ∥CD ， 即AB ∥CG ，∵CD ＝2AB ，CG ＝12CD ，∴AB ＝CG ，∴四边形ABCG 是平行四边形； （2）解：∵四边形ABCG 是平行四边形，AE ＝2，CG ＝3， ∴AG ∥BC ，AG ＝BC ，AB ＝CG ＝3， ∵∠GAD ＝90°， ∴∠AEB ＝90°，在Rt △ABE 中，由勾股定理可得：BE 22AB AE -即BE ＝22325-=，∵△AEB ∽△DEC ， ∴12BE AB CE CD ==， ∴CE ＝25，∴BC ＝BE+CE ＝35， ∴AG ＝BC ＝35．【点睛】本题考查相似三角形的性质，勾股定理，平行四边形的判定与性质，解题的关键是熟练掌握相似三角形的性质，勾股定理的运用，平行四边形的判定与性质．23．如图，在△ABC 中，AD 是角平分线，点E 是边AC 上一点，且满足ADE B ∠=∠．(1)证明：ADB AED ∆∆；(2)若3AE =，5AD =，求AB 的长． 【解答】(1)见解析(2)253【提示】（1）证出∠BAD=∠EAD ．根据相似三角形的判定可得出结论； （2）由相似三角形的性质可得出AD ABAE AD =，则可得出答案． （1）∵AD 是∠BAC 的角平分线， ∴∠BAD=∠EAD ． ∵∠ADE=∠B ， ∴△ADB ∽△AED ． （2）∵△ADB ∽△AED ， ∴AD ABAE AD =，∵AE=3，AD=5， ∴535AB =， ∴253AB =． 【点睛】本题考查了相似三角形的判定与性质以及三角形内角和定理，熟练掌握相似三角形的判定定理和性质定理是解题的关键．24．已知：平行四边形ABCD ，E 是BA 延长线上一点，CE 与AD 、BD 交于G 、F ．求证：2CF GF EF =⋅．【解答】见解析【提示】根据平行四边形的性质得到AD BC ∥，AB CD ∥，得到△DFG ∽△BFC ，△DFC ∽△BFE ，根据相似三角形的性质列出比例式，计算即可． 【详解】证明：∵四边形ABCD 是平行四边形， ∴AD BC ∥，AB CD ∥，∴△DFG ∽△BFC ，△DFC ∽△BFE ∴GF DF CF BF =，CF DFEF BF =， ∴GF CFCF EF =， 即2CF GF EF =⋅．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．25．如图，已知cm,cm,23,36,117AD a AC b BC AC B D ===∠∠=︒=︒，ABC DAC △∽△．（1）求AB 的长；（2）求DC 的长； （3）求BAD ∠的度数．【解答】（1）32cm a ；（2）2cm3b ；（3）153︒【提示】（1）由ABC DAC △∽△，可得：,AB BCAD AC =再代入数据可得答案；（2）由ABC DAC △∽△，可得：,AC BCDC AC =再代入数据可得答案；（3）由ABC DAC △∽△，可得：117,36,BAC D B DAC ∠=∠=︒∠=∠=︒再利用角的和差可得答案； 【详解】解：（1）23,,BC AC AD a ==3,2BC AC ∴= ABC DAC △∽△，,AB BCAD AC ∴= 3,2AB a ∴= 3.2AB a ∴=（2） ABC DAC △∽△，,AC BCDC AC ∴= 而3,,2BC AC b AC == 3,2b DC ∴=2.3DC b ∴=（3） ABC DAC △∽△，36,117,B D ∠=︒∠=︒117,36,BAC D B DAC ∴∠=∠=︒∠=∠=︒11736153.BAD BAC DAC ∴∠=∠+∠=︒+︒=︒【点睛】本题考查的是相似三角形的性质，掌握相似三角形的对应角相等，对应边成比例是解题的关键.26．如图，在四边形ABCD 中，AC ，BD 交于点F ．点E 在BD 上，且BAE CAD ∠=∠，AB ACAE AD =．(1)求证：ABC AED ∽△△． (2)若20BAE ∠=︒，求∠CBD 的度数． 【解答】(1)证明见解析 (2)20︒【提示】（1）根据两边对应成比例，且夹角相等，两个三角形相似，即可证明．（2）根据（1）中ABC AED ∽△△，得出ADB ACB ∠=∠，再根据对顶角相等，AFD BFC ∠=∠，证得AFD BFC ∽△△，得出CBD CAD BAE ∠=∠=∠，即可求解． （1）∵BAE CAD ∠=∠∴BAE EAF CAD EAF ∠+∠=∠+∠， ∴BAC DAE ∠=∠， AB ACAE AD =，∵在ABC 和AED △中， AB ACAE AD BAC DAE ⎧=⎪⎨⎪∠=∠⎩，∴ABC AED ∽△△． （2）∵ABC AED ∽△△， ∴ADB ACB ∠=∠，又∵AFD BFC ∠=∠，对顶角相等，∴AFD BFC ∽△△， ∴CBD CAD ∠=∠，∵BAE CAD ∠=∠，20BAE ∠=︒，∴20CAD ∠=︒， 故答案为：20︒．【点睛】本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键． 27．如图，四边形ABCD 为正方形，且E 是边BC 延长线上一点，过点B 作BF ⊥DE 于F 点，交AC 于H 点，交CD 于G 点．(1)求证：△BGC ∽△DGF ； (2)求证：GD AB DF BG ⋅=⋅； (3)若点G 是DC 中点，求GFCE 的值．【解答】(1)见解析 (2)见解析 (3)5GF CE=【提示】（1）由正方形性质和题干已知垂直条件得直角相等，后由对顶角相等，进而得到△BGC ∽△DCF ．（2）由第一问的结论可得到相似比，既有DG BC DF BG ⋅=⋅，然后因为正方形四边相等，进行等量代换即可求出证明出结论．（3）通过ASA 判定出△BGC ≌△DEC ，进而根据第一问结论可得△BGC ∽△DGF ，然后通过相似比设未知数，赋值CG x =，即可求出GFCE 的值．（1）证明：∵四边形ABCD 是正方形 ∴90BCD ADC ∠=∠=︒ ∵BF DE ⊥ ∴90GFD ∠=︒ ∴BCD GFD ∠=∠，又∵BGC DGF ∠=∠， ∴△BGC ∽△DCF ． （2）证明：由（1）知△BGC ∽△DGF ， ∴BG BCDG DF =， ∴DG BC DF BG ⋅=⋅ ∵四边形ABCD 是正方形， ∴AB BC =∴DG AB DF BG ⋅=⋅． （3）解：由（1）知△BCC ∽△DGF ， ∴FDG CBG ∠=∠，在△BGC 与△DEC 中，,{,=,CBG CDE BCG DCE BC CD ∠=∠∠=∠ ∴△BGC ≌△DEC （ASA ） ∴CG EC = ∵G 是CD 中点 ∴CG DG = ∴::GF CE CF DC = ∵△BGC ∽△DGF ∴::GF DG CG BG =在Rt △BGC 中，设CG x =，则2BC x =，BC =∴CG BG =∴GF CE=【点睛】本题主要考查了正方形的性质，全等三角形判定和性质，相似三角形判定和性质等知识点，熟练运用相似三角形判定和性质是解题的关键．28．如图1，在ABC 中，90ACB ∠=︒，AC BC =，点D 是AB 边上一点（含端点A 、B ），过点B 作BE 垂直于射线CD ，垂足为E ，点F 在射线CD 上，且EF BE =，连接AF 、BF ．（1）求证：ABF CBE ∽；（2）如图2，连接AE ，点P 、M 、N 分别为线段AC 、AE 、EF 的中点，连接PM 、MN 、PN ．求PMN ∠的度数及MNPM 的值；（3）在（2）的条件下，若2BC =PMN 面积的最大值．【解答】（1）证明见解析；（2）135PMN ∠=；=2MN PM 3）14 【提示】（1）根据两边对应成比例，夹角相等判定即可．（2）PMN ∠的值可以根据中位线性质，进行角转换，通过三角形内角和定理求解即可，MNPM 的比值转换为AFCE 的比值即可求得.（3）过点P 作PQ 垂直于NM 的延长线于点Q ，12PMN S MN PQ =△，将相关线段关系转化为CE ，可得关系218PMN S CE =△，观察图象，当2CE BC == 【详解】（1）证明：∵90ACB ∠=︒，AC BC = ∴2AB BC =,45ABC BAC ∠=∠= ∵BE 垂直于射线CD , ∴90,BEF ∠= 又∵EF BE =∴2FB EB =,45FBE EFB ∠=∠= ∵+ABC ABE ABE FBE ∠∠=∠+∠ 即：ABF CBE ∠=∠又∵2AB BFCB BE == ∴ABF CBE ∽（2）解：∵点P 、M 、N 分别为线段AC 、AE 、EF 的中点∴//PM CN ，//MN AF ，11,22PM CE MN AF== ∴MPN CNP ∠=∠,CNM EFA ∠=∠∴+MPN MNP CNP MNP CNM EFA ∠∠=∠+∠=∠=∠ 又∵ABF CBE ∽ ∴90AFB CEB ∠=∠= 又∵45EFB ∠=∴904545EFA AFB BFE ∠=∠-∠=-= ∴+45MPN MNP ∠∠=又∵++180MPN MNP PMN ∠∠∠= ∴18045135PMN ∠=-=又∵12=12AFMN AFPM CECE = 又∵ABF CBE ∽ ∴=2AF AB CE CB = ∴=2MNPM（3）如下图：过点P 作PQ 垂直于NM 的延长线于点Q , 135,PMN ∠=︒ 45,PMQ MPQ ∴∠=︒=∠,PQ ∴= 111221222228216PMNS MN PQ AF PM AF CE AF CE ==⨯⨯==△又∵BC =∴AF =∴221168PMN S CE ==△∴当CE 取得最大值时，PMN 取得最大值， ,BE CE ⊥E ∴在以BC 的中点为圆心，BC 为直径的圆上运动，∴当CE CB ==CE 最大，∴11=2=84S ⨯， 【点睛】本题考查的是三角形相似和判定、以及三角形面积最大值的求法，根据题意找见相关的等量是解题关键．。

相似三角形的基本图形及其运用作者：蒋丽萍来源：《中学教学参考·语英版》2012年第02期相似三角形是初中几何中的核心模块，是中考中的重要考点，也是考查学生分析问题和解决问题的综合能力的重要载体.相似三角形中有一些基本图形，如果能掌握这些基本图形，并把它们从复杂的图形中挖掘出来，构成几何问题中的核心结构，问题的解决也就水到渠成.首先我们来扫描一下相似三角形的基本图形一、常规基本图形1.平行型此类型有两种基本图形：简称“A”型图和“X”型图【例1】已知：如右图，直线l的解析式为y=43x+4,l与x轴、y轴分别交于点A、（1）求原点O到直线l的距离（2）有一个半径为1的⊙C从坐标原点出发，以每秒1个单位长度的速度沿y轴正方向运动，设运动时间为t（秒）,当⊙C与直线l相切时，求t的值解析：（1）过点O作OH⊥AB于点H，利用等积法可求出斜边上的高OH，即原点O到直线l的距离为(2)当⊙C与直线l相切时,点C到直线l的距离等于⊙C的半径1，而点C的位置可能在点B的下方或上方，因此要分两种情况进行讨论①当点C的位置在点B的下方时，过点C作CG⊥AB于点G,则得到基本图形1，利用△BCG∽△BOH，得到BC4=1125，求出BC=53，再求出OC=73，由1·t=73就可求出t=73（秒）；②当点C′的位置在点B的上方时，过点C′作C′G′⊥直线l于点G′,则得到基本图形2，利用△BC′G′∽△BOH，同①得到BC′=53，再求出OC′=173，求出t=173（秒）点评：此题中既用到了型图又用到了型图.从不同的视角分析图形，找准切入点，也就成了解决问题的关键2.相交型此类型也有两种基本图形：简称斜型图和斜型图如图3，△ABC中，点D、E分别在AB、AC上，若∠ADE=∠ACB（或∠AED=∠ABC）,则△ADE∽△特别地，当点E与点C重合时，又得到了如图4所示的基本图形如图5，线段AD、BC相交于点E，连结AB、CD，若∠A=∠C（或∠B=∠D）,则△ABE∽△【例2】已知：如右图，矩形ABCD中，AC、BD交于点O，OF⊥AC于O交BA于点E，交CB的延长线于点F.求证解析：欲证，可寻找这四条线段所在的两个三角形，证出这两个三角形相似即可.连结AF得基本图形4，利用矩形的性质及OF⊥AC可证出∠1=∠2，又∠2+∠3=∠4+∠，所以∠4=∠2=∠1，所以△AOE∽△FOA，结论即可得证点评：由结论找到（或构造）要证的基本图形，追根寻源，问题迎刃而解【例3】已知：如右图，在⊙O中弦AB、CD相交于点E，若AB=10，CD=12，且点E是AB的中点，则点E也是CD的中点吗？为什么？解析：由题意可知，图中有基本图形5（这是圆中常用到的基本图形），利用△ACE∽△DBE得到512-CE=CE5，求出CE=6-11,DE=6+11,因此得出点E不是CD的中点点评：回归基本图形，以算代证，快速解决问题3.双垂直型（也称母子相似三角形）双垂直型图运用相当广泛，结合勾股定理，图中共有6条线段，只要已知其中的任意2条线段的长就可求出其余的4条线段来【例4】已知：如右图，C是半圆O上一点，，过点C作直径AB的垂线CP，P为垂足，弦AE分别交PC、CB于点D、F.(1)求证：；(2)求证：AD=CD；（3）若DF=54，DPAP=34,求PB的长解析：（1）欲证，需证△ACD∽△AEC，而这正是一个特殊的斜型图，即基本图形4，由条件证出∠ACD=∠B=∠AEC即可（2）由可得AC=CE,从而∠CAD=∠AEC=∠ACD，结论得证（3）可证出AD=CD=54，由DPAP=34,可得DP=34，AP=1，CP=2,图中有基本图形6，利用△CPA∽△BPC,得到12=2PB，从而求出点评：此题中既用到了特殊的斜型图又用到了双垂直型图，所以挖掘基本图形对于解题很重要二、特殊基本图形1.和为平角型如图7，点E在BC上，若∠AED=∠B=∠C，则△ABE∽△ECD.这个基本图形在几何综合图形中经常出现.特别地，当∠AED=∠B=∠时，又得到了如图8所示的基本图形【例5】已知：如右图，在梯形ABCD中，AD∥BC,AD=2,BC=4,点M是AD的中点，△MBC是等边三角形（1）求证：梯形ABCD是等腰梯形；（2）动点P、Q分别在线段BC和MC上运动，且∠保持不变，设PC=x，MQ=y，求y与x的函数关系式；（3）在（2）中当y取最小值时，判断△PQC的形状，并说明理由解析：（1）由条件可证△ABM≌△DCM,得到AB=DC,从而结论得证.（2）图中存在基本图形7，利用△CPQ∽△BMP，得到x4=4-y4-x，从而求得-x+4；（3）利用二次函数的最值可求出当x=2时，最小值y=3，证得△PQC为直角三角形点评：从复杂图形中挖掘出特殊基本图形的方法就是要熟悉这些特殊的基本图形.拓展延伸如右图，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME 和矩形ACNF，射线GA交EF于点H.若AB=kAE，AC=kAF，试探究HE与HF之间的数量关系，并说明理由解析：（问题探究） k=1时，易证△ABG≌△，得到AG=EP，同理AG=FQ，所以（拓展延伸）过点E作EP⊥GA，FQ⊥GA，垂足分别为P、Q，则得到基本图形8，利用△ABG∽△EAP，得到AGEP=ABEA，同理AGEP=ACFA.由AB=kAE，AC=kAF，得到ABEA=ACFA=k，从而EP=FQ.再由∠EHP=∠FHQ，得到△EPH≌△FQH，所以点评：此题一开始就将两个全等的直角三角形拼成了貌似图8的基本图形，然后一步步去构造出了含有两对此全等形的复杂图形，最后真正演变成了相似三角形中两个图8这样的基本图形，万变不离其宗2.和为直角型【例6】已知：如下图，四边形中，∠BAD=∠，CD=92,求四边形ABCD的面积解析:因为∠所以过点D作DE⊥AC于E，则得到基本图形9，利用△ABC∽△DAE，得AEBC=DEAC=ADAB=34.设AE=3k,则BC=4k,AC=12k,CE=9k,DE=9k，因为CD=92，所以k=1，可求得四边形ABCD的面积为点评：以和为直角型图形为依托，利用相似比例关系还原线段长度后定出面积大小由以上问题不难看出，识别并会利用相似三角形中的基本图形对解决几何问题是相当重要的.在解几何题时用好几何图形中的基本图形，可以有效解决问题并加深对问题本质的理解，从而达到提高解决综合问题能力的目的，正如华罗庚先生所言：不断积累，飞跃必来，突破随之（责任编辑金铃）。

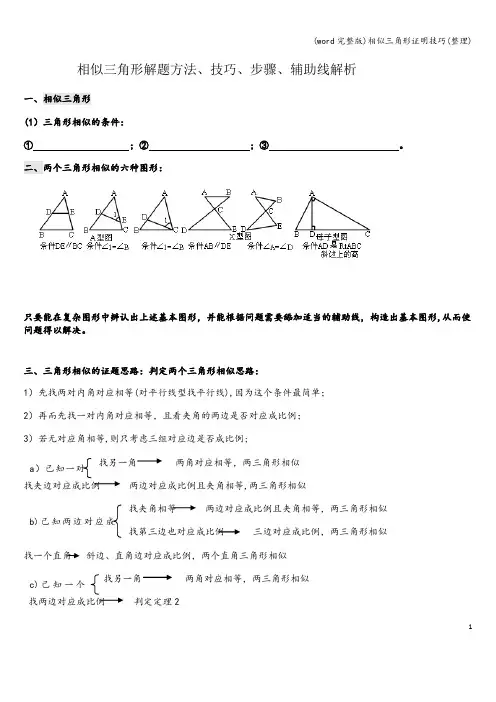
1相似三角形解题方法、技巧、步骤、辅助线解析一、相似三角形(1）三角形相似的条件：① ；② ；③ 。

二、两个三角形相似的六种图形：只要能在复杂图形中辨认出上述基本图形，并能根据问题需要舔加适当的辅助线，构造出基本图形,从而使问题得以解决。

三、三角形相似的证题思路：判定两个三角形相似思路：1）先找两对内角对应相等(对平行线型找平行线),因为这个条件最简单； 2）再而先找一对内角对应相等，且看夹角的两边是否对应成比例； 3）若无对应角相等,则只考虑三组对应边是否成比例; 找另一角 两角对应相等，两三角形相似找夹边对应成比例 两边对应成比例且夹角相等,两三角形相似找夹角相等 两边对应成比例且夹角相等，两三角形相似找第三边也对应成比例 三边对应成比例，两三角形相似找一个直角 斜边、直角边对应成比例，两个直角三角形相似 找另一角 两角对应相等，两三角形相似找两边对应成比例 判定定理2a ）已知一对b)己知两边对应成c)己知一个2找顶角对应相等 判定定理1找底角对应相等 判定定理1找底和腰对应成比例 判定定理3e ）相似形的传递性 若△1∽△2，△2∽△3，则△1∽△3四、“三点定形法”，即由有关线段的三个不同的端点来确定三角形的方法。

具体做法是：先看比例式前项和后项所代表的两条线段的三个不同的端点能否分别确定一个三角形，若能,则只要证明这两个三角形相似就可以了，这叫做“横定”;若不能，再看每个比的前后两项的两条线段的两条线段的三个不同的端点能否分别确定一个三角形，则只要证明这两个三角形相似就行了，这叫做“竖定”。

有些学生在寻找条件遇到困难时,往往放弃了基本规律而去乱碰乱撞,乱添辅助线，这样反而使问题复杂化，效果并不好，应当运用基本规律去解决问题。

例1、已知：如图，ΔABC 中，CE ⊥AB ，BF ⊥AC. 求证: BAAC AF AE（判断“横定”还是“竖定”？ ）例2、如图,CD 是Rt △ABC 的斜边AB 上的高，∠BAC 的 平分线分别交BC 、CD 于点E 、F ，AC ·AE=AF ·AB 吗？ 说明理由。

《相似三角形的应用》讲义一、相似三角形的定义及性质相似三角形是指对应角相等，对应边成比例的两个三角形。

相似三角形具有以下重要性质：1、对应角相等：两个相似三角形的对应角大小相等。

2、对应边成比例：相似三角形的对应边的长度比值相等。

3、周长比等于相似比：两个相似三角形的周长之比等于它们的相似比。

4、面积比等于相似比的平方：相似三角形的面积之比等于相似比的平方。

这些性质是解决相似三角形应用问题的基础，我们要牢记并熟练运用。

二、相似三角形在实际生活中的应用1、测量高度在实际生活中，我们常常需要测量一些物体的高度，如大树、高楼等，而直接测量往往比较困难。

这时就可以利用相似三角形的知识来解决。

例如，要测量一棵大树的高度，我们可以在与大树底部水平的地面上立一根标杆，然后测量出标杆的长度以及标杆和大树的影长。

由于太阳光线是平行的，所以标杆和大树与地面形成的三角形是相似的。

设标杆高为 a，标杆影长为 b，大树影长为 c，则根据相似三角形的性质，可得大树的高度为：＼（H ＝＼frac{ac}｛b}＼）2、测量距离相似三角形还可以用于测量无法直接到达的两点之间的距离。

比如，要测量一条河的宽度，我们可以在河的一侧选定一个点 A，在对岸选定一个点 B，然后在河的这一侧再找一个点 C，使得 AC 垂直于河岸。

接着，在 AC 的延长线上找一个点 D，使得 B、D 两点的连线经过点 C。

测量出 AC、CD 的长度。

因为三角形 ABC 和三角形 ADC相似，所以根据相似比可以计算出河宽 AB 的长度。

3、计算角度在一些几何问题中，通过相似三角形的关系可以计算出未知的角度。

例如，已知两个相似三角形的对应边的夹角，通过相似三角形对应角相等的性质，可以求出其他角的大小。

三、相似三角形在工程中的应用1、建筑设计在建筑设计中，相似三角形的原理被广泛应用。

比如，设计师在设计楼梯时，需要考虑楼梯的坡度和踏步的高度、宽度等比例关系，以保证楼梯的安全性和舒适性。

相似三角形的九大模型相似三角形是几何学中一类重要的图形，它具有一些独特的性质和模型。

这些模型可以用来解决各种实际问题，从简单的长度关系到复杂的空间结构。

本文将介绍相似三角形的九大模型，并给出相应的例子和应用场景。

相似三角形是指两个三角形形状相同，大小成比例。

相似三角形的对应边成比例，对应角相等。

相似三角形还有一些其他的性质，例如，相似三角形的中线、角平分线、高的比等于它们的相似比。

平行线模型：两个三角形分别在两条平行线上，它们的对应边平行且成比例。

这种模型经常用于解决一些与长度和角度相关的问题。

共顶点模型：两个三角形有一个共同的顶点，且它们的对应边成比例。

这种模型常用于证明两个三角形相似，以及求解一些角度问题。

角平分线模型：一个三角形的角平分线将这个三角形分成两个小的相似三角形。

这种模型可以用于证明两个三角形相似，以及求解一些角度问题。

平行四边形模型：一个平行四边形被它的两条对角线分成四个小的相似三角形。

这种模型可以用于解决一些与面积和长度相关的问题。

位似模型：一个相似变换将一个三角形映射到另一个三角形，这种变换称为位似变换。

这种模型可以用于解决一些与长度、角度和面积相关的问题。

旋转模型：一个三角形绕着它的一个顶点旋转一定的角度后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与角度和长度相关的问题。

镜像模型：一个三角形沿一条直线翻折后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与长度和角度相关的问题。

传递模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分相似。

这种模型可以用于解决一些与长度和角度相关的问题。

扩展模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分成比例。

这种模型可以用于解决一些与长度和角度相关的问题。

相似三角形的九创作者是几何学中一类重要的模型，它们具有广泛的应用价值。

课题：相似三角形的基本图形及其应用 【学习目标】1.梳理归纳常见相似中的基本图形2.灵活应用相似的相关知识解决一些问题【重点难点】熟悉相似中的基本图形并能灵活运用 【导学指导】 （一）知识链接常见基本图形及常用结论①A 型或X 型(1)可以看作“平行线分比例定理”的推论 (2)A 型：DE ∥△ADE ∽△DE BC＝AD AB{ABADBC DE ABC ADE BC DE X BD BACDAE =⇒⇒⇒∠=∠∠=∠∽△△∥型： (3)点D 是中点点E 也是中点②直角三角形斜边上的高（1）△ACD ∽△CBD ∽△ABC （2）射影定理：AC 2=AD ·ABBC 2=BD ·AB DC 2=AD ·DBABC EDABCDABCDE（3）利用 DB CD＝CD AD＝BCAC 合理地设出参数k若AC=3BC ，则 ADDB＝③母子相似（1）∠1＝∠2→△BCD ∽△ACB →CDBC＝BCAC→BC 2=CD ·AC 以上结论反过来也成立。

（2）∠1＝∠2→△AED ∽△ABC →AD AC＝AEAB→AD ·AB=AE ·AC 以上结论反过来也成立。

④利用直角三角形（或直角）构造相似AMCN ＝CMBN ＝ACBC ＝tanBACB D12ACBD1 2EABCMN lABCMNl（二）自主学习【例题】（八下课本68页第8页）已知在正方形ABCD 中，E 、F 分别是AD 、CD 边上的两点，且DE ＝CF ，问线段BE ，AF 有何关系，并说明理由。

【变式1】 若E 、F 分别是AD 、CD 的中点求：(1)BG AG 的值 (2)GF AG 的值（3） GFBG (用两种．．不同的方法）ABCDEF ABCDFGEABCDFGE【变式2】 若再连GC ，用多种．．方法证明：552 BE CG【变式3】若正方形的边长为4，经过AF 的中点G 作直线交边AD 于P ，交边BC 于Q 且AF=PQ ，求AP 的长。