单位阶跃信号的表示

O
t
宗量>0，函数值为1； 宗量<0，函数值为0。
（2）有延迟的单位阶跃信号
u(t
t0
)
0 1
t t
t t
0 0
,
t
0
0
由宗量 (t-t0)=0，可知 t=t0 时，即时 间为 t0 时，函数有断点、跳变点
u(t t0 ) 1
O
t0
t
5
3. 单位阶跃信号
(3) 用单位阶跃信号描述其他信号 门函数(Gate)：也称矩形窗函数
第一章 信号与系统分析导论
1.5 阶跃信号与冲激信号
1
主要内容
奇异信号
l 单位斜变信号 l 单位阶跃信号 l 单位冲激信号 l 冲激偶信号
2
1. 奇异信号
函数本身有不连续点(跳变点)或其导数与积分 有不连续点的一类函数统称为奇异信号或奇异 函数。
单位斜变 信号
单位冲激 信号
单位阶跃 信号
冲激偶 信号
4
2. 单位斜变信号
（1） 定义
R(t )
R(t
)
0 t
t0 t0
1
O1
t
（2）有延迟的单位斜变信号
R(t
t0
)

t
0 t0
t t0 t t0
R(t t0 ) 1
O t0 t0 1 t
由宗量t t0 0可知起始点为t0
4
3. 单位阶跃信号
（1）定义
u(t )
u(t )
0
1
t0
1
t 0 0点无定义或1/2
G
t
u
t
2
u
t
2

设x(t)在t=0与t0处连续，
x(t)(t) x(0)(t)
x(t)
t
(1) (1)
0
t0
t
x(t)(t t0 ) x(t0 )(t t0 )
(x(t0 )) (x(0))


0
t0
t
x(t)(t)dt x(0) (t)dt x(0)




x(t)(t t0)dt x(t0 ) (t t0 )dt x(t0 )
t
2
2
u(t ) u(t )
2
2
2、单位斜变信号：R(t)
R(t)
函数式：
R(t)

t 0
t 0 t 0
波形图：
1 01
t
tu(t)
平移： R(t t0 ) (t t0 )u(t t0 )
R(t t0 )
1
0 t0 1 t0
t
•与单位阶跃信号的关系：


⑵ 偶函数：
(t) (t)
(t t0 ) [(t t0 )] (t0 t)
•单位冲激信号的导数（微分）：
单位冲激信号的各阶导数（微分）表示为：
(t) d(t) dt
(t) d(t) dt
(t)

d(t) dt

•由阶跃信号表示的典型信号：
⑴ 符号函数信号： sgn(t)
sgn(t
)

1 1
t 0 t0
u(t) u(t)
2u(t) 1
sgn(t)
1
0
t
1
⑵ 矩形脉冲信号： G (t)--门函数信号

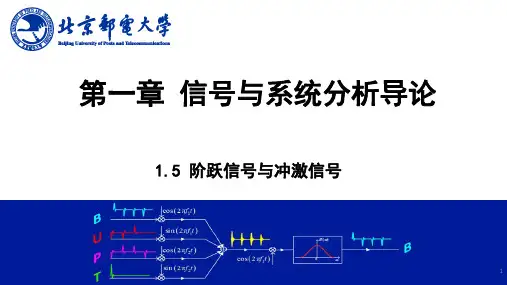
单位阶跃信号表达式单位阶跃信号是信号与系统中的重要概念，也是一种特殊的信号形式。

在信号与系统分析中，单位阶跃信号通常用符号u(t)表示，它在t=0时跃变为1，在t<0时为0。

单位阶跃信号在实际生活中有着广泛的应用，例如在电路中的开关电路、控制系统中的反馈环节等都会涉及到单位阶跃信号的使用。

让我们来理解什么是单位阶跃信号。

单位阶跃信号是一种理想化的信号，它在t=0时突变为1，此前一直为0。

可以将单位阶跃信号看作是一个理想的开关，表示在某个时刻突然发生的事件。

单位阶跃信号在电路中有着重要的应用。

例如，在开关电路中，当开关关闭时，电路中的电流为0；当开关突然打开时，电路中的电流会突变为正值，这个过程可以用单位阶跃信号来描述。

在控制系统中，单位阶跃信号常用于测试系统的稳定性和响应特性。

通过给系统输入单位阶跃信号，可以观察系统的输出响应，并从中得到系统的特性参数。

单位阶跃信号还可以用于描述系统的冲击响应。

冲击响应是指系统对一个瞬时冲击信号的响应，可以用单位阶跃信号的导数来表示。

在信号与系统分析中，我们经常使用冲击响应函数来描述线性时不变系统的特性，而单位阶跃信号在其中起到了重要的作用。

除了在电路和控制系统中的应用，单位阶跃信号还可以用于信号处理领域。

在数字信号处理中，单位阶跃信号常用于测试系统的频率响应和滤波器的特性。

通过对单位阶跃信号进行傅里叶变换或者Z 变换，可以得到系统的频率响应函数，从而了解系统对不同频率信号的处理能力。

在实际应用中，单位阶跃信号常常与其他信号进行组合。

例如，可以将单位阶跃信号与正弦信号相乘，得到一种脉冲信号。

这种脉冲信号在通信系统中有着重要的应用，可以用于数据传输和调制解调等方面。

单位阶跃信号是信号与系统分析中的重要概念，具有广泛的应用。

它可以用于描述电路中的开关过程、控制系统的响应特性、系统的冲击响应和频率特性等。

在实际应用中，单位阶跃信号常常与其他信号进行组合，形成更加复杂的信号形式。

1 sgn( t) 1 t 0 t 0

O
2

2
sgn t
1
O
t
-1
1 sgn( t ) u ( t ) u ( t ) 2 u ( t ) 1 u ( t) [sgn( t) 1 ] 2
三．单位冲激δ(t)（难点）
概念引出 定义1 定义2 冲激函数的性质
冲激导数的抽样情况：利用分部积分运算

(t)f(t) d t


f ( t ) ( t ) ( t ) ( t ) d t f
f(0 )
3.冲激偶（冲激的导数）
s( t )
1
(t )

1
成为
(1)
O
o
求导
s( t )
集美大学信息工程学院201041414阶跃信号和冲激信号阶跃信号和冲激信号信号函数本身有不连续点跳变点或其导数与积分有不连续点的一类信号函数统称为奇异信号或奇异函数
§1.4 阶跃信号和冲激信号
集美大学信息工程学院 2010.4
本节介绍
信号（函数）本身有不连续点(跳变点)或其导 数与积分有不连续点的一类信号（函数）统称为 奇异信号或奇异函数。 主要内容： •单位斜变信号 •单位阶跃信号 •单位冲激信号 •冲激偶信号
0 u ( t t ) 0 1
t
u( t t 0 )
1
O
1
t t 0 , t 0 0 t t 0
0
t0 u(t t0 )
t
由宗量 t O t t 0 可 t 知 t , 即 时 0 0 ，函数有断点，跳变点 间为 t0 时 宗量>0 函数值为1 宗量<0 函数值为0

若u1和u2有限值，则有 C1u1(o ) C1u1(o ) C2u2 (o ) C2u2 (o )
C1u1(o ) C2u2 (o ) C1u1(o ) C2u2 (o ) u1(o ) u2 (o ) Us
电容电压初始值：
u1(o )
C2 C1 C2
Us
u2 (o )
C1 C1 C2
(0 ) 1 C
uc (0 )
t
i
0
1
C
c ()d
0
ic ()d
0
若ic有限，则： uc (o+)= uc (o-)
或 q (o+)= q (o-)
意义：
能量不能发生突变
4
2、引例2: 图示电路
t<0 ，K打开，有 iL (0 ) 0
t=0 ，K闭合，有
iL (t)
1 L
t
uL ()d
若uL有限，则： iL (o+)=iL (o-)
1 0
1t
L
uL ()d
L
uL ()d
0
或 (o+)= (o-)
i
L
(0
)
iL
(0 ) iL (0
)
1 L
t
uL ()d
0
1
L
0 0
u
L
()d
意义：
能量不能发生突变
5
3、换路定律： （1）若ic有限，则： uc (o+)= uc (o-) 或q (o+)= q (o-) （2）若uL有限，则： iL (o+)=iL (o-) 或 (o+)= (o-)
i2 (0 ) 3A

例子
0 (当t 2 ) 1 vc (t ) (t ) (当 t ) 2 2 2 1 (当t ) 2 电流ic(t)为
：
从物理方面理解函数的意义。电路图如下： 电压源vc(t)接向电容元件Ｃ，假定vc(t)是斜变信号。
vc (t )

ic (t )
c
vc (t )
ic (t )
dvc (t ) ic (t ) c dt c [u (t ) u (t )] 2 2
1
1 2
c
2
0 2
t

0 2
t 0 2
t
如果0的极限情况，则vc(t)成为阶跃信号，它的微分— —电流ic(t)是冲激函数其表达式为： vc (t ) u (t ) v (t )
信号与系统
孔艳岩
495239861
1.4 阶跃信号和冲激信号 1.单位斜变信号
斜变信号也称斜升信号。 它是从某一时刻开始随时间正比例增长的信号。 如果增长的变化率是1，就称为单位斜变信号。

(1)单位斜变信号
f (t )
如果将起始点移至t0,则可写成
0 t 0 f (t ) t t 0
1
0
1
t
与阶跃函数类似，对于符号函数在跳变点也可不予定义，或 规定sgn(0)=0. 显然，阶跃信号来表示符号函数
sgn( t ) 2u (t ) 1
2、阶跃函数的性质：
（1）可以方便地表示某些信号
f(t) = 2u(t)- 3u(t-1) +u(t-2)
（2）用阶跃函数表示信号的作用区间

x(t)dt 2
Ae
(
t
)
2
dt
2A
A
0
2
二、离散时间信号：
1、单位样值序列： (n)
函数式：
(n)
1 0
n0 n0
波形图：
(n)
1
0
n
位移：
1 (n n0 ) 0
n n0 n n0
(n n0)
1
0 n0
n
• 抽样性：
设有序列x(n) ，则有
x(n)
1 2 0
12 3 4 5
n
x(t)
1
x(t)
1
x(t)
(1)
0
x(t)
x(t)
1
1
t
2
2
t
0
t
x(t)
1
x(t)
1
t
22
t
0
t
单位冲激信号在信号与系统的理 论中，是一个重要的基本信号，与 t 运动学中的质点、电学中的点电荷 一样，是一个理ቤተ መጻሕፍቲ ባይዱ的模型。
•单位冲激信号的性质： ⑴ 抽样性（筛选性）：
设x(t)在t=0与t0处连续，
• 欧拉公式：
cos t 1 (e jt e jt ) 2
e jt cos t j sin t
sin t 1 (e jt e jt ) 2j
e jt cos t j sin t
正余弦信号是我们熟悉的常用基本信号，它有很好的特 性，与指数信号类似，它们的导数和积分依然是正余弦信 号，在正弦交流电路分析中我们知道，角频率为Ω的正弦 信号作用于电路，其输出还是角频率为Ω的正弦信号。
称为它们的初相位，Ω是它们的角频率。

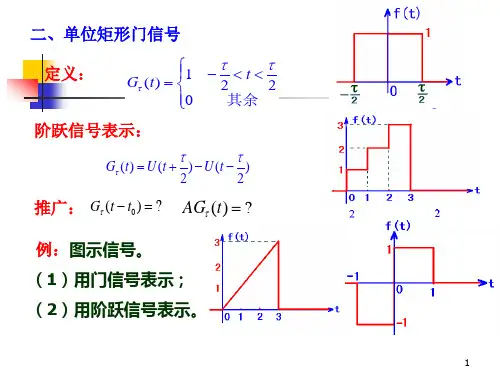
单位阶跃信号单位阶跃信号的定义为：单位阶跃信号是信号分析的基本信号之一，在信号与系统分析中有着非常重要的作用，通常，我们用它来表示信号的定义域，简化信号的时域表示形式。

例如：可以用两个不同延时的单位阶跃信号来表示一个矩形门信号，即：在MATLAB中，可通过多种方法得到单位阶跃信号，下面分别介绍主要的几种。

方法一：调用Heaviside(t)函数在MATLAB的Symbolic Math Toolbox 中，有专门用于表示单位阶跃信号的函数，即Heaviside(t)函数，用它即可方便地表示出单位阶跃信号以及延时的单位阶跃信号，并且可以方便地参加有关的各种运算过程。

例①．用MATLAB画出单位阶跃信号的波形，其程序如下：ut=sym('Heaviside(t)'); %定义单位阶跃信号（要用符号函数定义法）ezplot(ut,[-2,10]) %绘制单位阶跃信号在范围之间的波形运行结果如下：例②．用MATLAB画出信号的波形其程序如下：f=sym('Heaviside(t+2)-3*Heaviside(t-5)'); %定义函数表达式ezplot(f,[-4,20]) %绘制函数在范围之间的波形运行结果如下：方法二：数值计算法在MATLAB中，有一个专门用于表示单位阶跃信号的函数，即stepfun( )函数，它是用数值计算法表示的单位阶跃函数。

其调用格式为：stepfun(t,t0) 其中，t是以向量形式表示的变量，t0表示信号发生突变的时刻，在t0以前，函数值小于零，t0以后函数值大于零。

有趣的是它同时还可以表示单位阶跃序列，这只要将自变量以及取样间隔设定为整数即可达到。

下面通过一个例子来说明如何调用stepfun( )函数来表示单位阶跃函数。

例①：用stepfun( )函数表示单位阶跃信号，并绘出其波形程序如下：t=-1:0.01:4; %定义时间样本向量t0=0; %指定信号发生突变的时刻ut=stepfun(t,t0); %产生单位阶跃信号plot(t,ut) %绘制波形axis([-1,4,-0.5,1.5]) %设定坐标轴范围运行结果如下：例②：绘出门函数的波形程序如下：t=-4:0.01:4; %定义时间样本向量t1=-2; %指定信号发生突变的时刻u1=stepfun(t,t1); %产生左移位的阶跃信号 (t+2) t2=2; %指定信号发生突变的时刻u2=stepfun(t,t2); %产生右移位的阶跃信号 (t-2) g=u1-u2; %表示门函数plot(t,g) %绘制门函数的波形axis([-4,4,-0.5,1.5]) %设定坐标轴范围-4<x<4 ，-0.5<y<1.5运行结果如下：方法三: 定义matlab函数u.m为function y = u(n)y = (n>=0);。

阶跃信号傅里叶变换的多种求解方法阶跃信号是一种具有明显跳跃变化的信号，通常在控制系统、通信系统等领域中被广泛应用。

在信号处理中，傅里叶变换是一种常用的信号分析方法，可以将时域信号转换为频域信号，从而方便进行滤波、频率分析等处理。

本文将介绍阶跃信号傅里叶变换的多种求解方法，包括：1. 基本公式法阶跃信号可以表示为一个单位阶跃函数和一个常数的和，即： f(t) = k + u(t)其中，k为常数，u(t)为单位阶跃函数。

根据傅里叶变换的基本公式，可得：F(ω) = ∫[k + u(t)]e^(-jωt)dt= k∫e^(-jωt)dt + ∫u(t)e^(-jωt)dt= kπδ(ω) + 1/jω + πδ(ω) (其中，δ(ω)为狄拉克δ函数)= (k + 1/2)πδ(ω) + 1/jω2. 分段法阶跃信号可以分段表示为：f(t) = {k, t<0; k+1, t≥0}根据傅里叶变换的线性性，可将f(t)分解为两个信号的和：f(t) = kδ(t) + (k+1)u(t)其中，δ(t)为单位冲激函数。

根据傅里叶变换的性质，可得：F(ω) = k + (k+1)/jω + π(k+1)δ(ω)3. 积分法将阶跃信号表示为积分形式：f(t) = k + ∫u(t')dt'根据傅里叶变换的积分性质，可得：F(ω) = kπδ(ω) + 1/jω·[1-e^(-jωt)]/(jω)= (k+1/2)πδ(ω) + 1/jω - (1/2πjω)·e^(-jωt) 其中，δ(ω)为狄拉克δ函数。

以上即为阶跃信号傅里叶变换的三种求解方法，可以根据不同情况选择合适的方法进行求解。

同时，需要注意的是，在计算过程中要注意分段和积分的边界条件，以及狄拉克δ函数的性质和定理的应用。

7
iL (o-)= 5A
13-3 电荷守恒与磁链守恒
一、电荷守恒定律 引例：图示电路 a
+ u1
- + u2 -
t<0 ，K打开，电路稳定，有 u 1 (0 ) 0 u 2 ( 0 ) 0 t=0 ，K闭合，在节点a有
u1 du u du2 C1 1 2 C2 R1 dt R2 dt
u c (0 ) u c (0 ) 18V

t o 等效电路 :
i1 (o ) 0, i 2 (o ) 3A


ic

i c (o ) 1A
u L 2 (o ) 9V u L1 (o ) 15V
u L1 u L2

14
电路初始值确定
电路初始值
t=0，K闭，有
u c (0 ) u c (0 ) 18V
L1 、 L2 和 is =3A组成割集，由磁链守恒定律，有
L1i1 (o ) L 2i 2 (o ) L1i1 (o ) L 2i 2 (o ) 又 i1 (o ) i 2 (o ) 3 0 i1 (o ) 0, i 2 (o ) 3A
i L (0 ) i L (0 ) 1A
o+等效电路:
ic (o+)

i c (o ) i L (o ) 1A
u R (o ) 8V

+
uR -
u L (o ) 0 i 2 (o ) Байду номын сангаас 0
u 2 (o ) 0
16
练习: 图示电路，t<0，K在1，电路稳定，t=0，K从1到2。

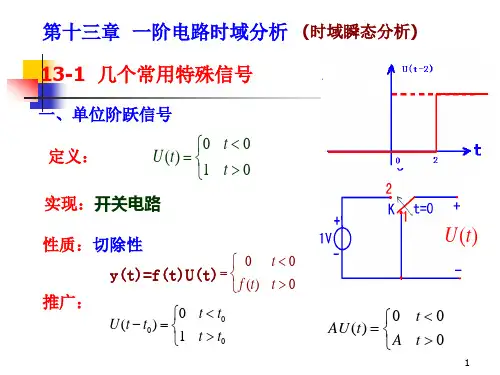
单位阶跃信号的表示-matlab————————————————————————————————作者：————————————————————————————————日期：单位阶跃信号单位阶跃信号的定义为：单位阶跃信号是信号分析的基本信号之一，在信号与系统分析中有着非常重要的作用，通常，我们用它来表示信号的定义域，简化信号的时域表示形式。

例如：可以用两个不同延时的单位阶跃信号来表示一个矩形门信号，即：在MATLAB中，可通过多种方法得到单位阶跃信号，下面分别介绍主要的几种。

方法一：调用Heaviside(t)函数在MATLAB的Symbolic Math Toolbox 中，有专门用于表示单位阶跃信号的函数，即Heaviside(t)函数，用它即可方便地表示出单位阶跃信号以及延时的单位阶跃信号，并且可以方便地参加有关的各种运算过程。

例①．用MATLAB画出单位阶跃信号的波形，其程序如下：ut=sym('Heaviside(t)'); %定义单位阶跃信号（要用符号函数定义法）ezplot(ut,[-2,10]) %绘制单位阶跃信号在范围之间的波形运行结果如下：例②．用MATLAB画出信号的波形其程序如下：f=sym('Heaviside(t+2)-3*Heaviside(t-5)'); %定义函数表达式ezplot(f,[-4,20]) %绘制函数在范围之间的波形运行结果如下：方法二：数值计算法在MATLAB中，有一个专门用于表示单位阶跃信号的函数，即stepfun( )函数，它是用数值计算法表示的单位阶跃函数。

其调用格式为：stepfun(t,t0) 其中，t是以向量形式表示的变量，t0表示信号发生突变的时刻，在t0以前，函数值小于零，t0以后函数值大于零。

有趣的是它同时还可以表示单位阶跃序列，这只要将自变量以及取样间隔设定为整数即可达到。

下面通过一个例子来说明如何调用stepfun( )函数来表示单位阶跃函数。

信号与系统公式总结信号与系统是电子信息类专业中非常重要的一门课程，它是基于数学和工程学原理的理论与实践的结合。

信号与系统公式总结作为这门课程的核心内容，在学习和应用中起着重要的作用。

下面将对信号与系统中的常用公式进行总结，以供参考。

一、信号及其表示公式1. 常数信号: x(t) = A (常数值 A)2. 常函数信号: x(t) = A, t∈[t1, t2]，否则 x(t)=0，其中 t1<t<t23. 正弦信号: x(t) = A*sin(ωt+θ)，其中A为振幅，ω为角频率，θ为初相位4. 余弦信号: x(t) = A*cos(ωt+θ)，其中A为振幅，ω为角频率，θ为初相位5. 单位阶跃信号: u(t) = 1，t≥0，否则 u(t) = 06. 单位冲激信号: δ(t) = 0，t≠0，否则δ(t) = ∞二、信号运算公式1. 平移公式: y(t) = x(t-T) (平移单位为 T，右移 T 为正，左移 T 为负)2. 缩放公式: y(t) = A*x(a*t) (缩放比例为 a，若 a>1，信号变化幅度增大；若0<a<1，信号变化幅度减小)3. 均值公式: RMS = sqrt((1/T)*∫(x(t)^2)dt) (T为时间区间，x(t)为信号函数)4. 线性运算公式: y(t) = a*x(t) + b*y(t) (y(t)表示输出信号，x(t)表示输入信号，a和b为常数)5. 卷积公式: y(t) = ∫[x(τ)*h(t-τ)]dτ (卷积公式是时间域中输入信号和系统响应的乘积积分，表示系统的输出)三、系统性质与稳定性公式1. 线性性质: L(a*x1(t)+b*x2(t)) = a*L(x1(t)) + b*L(x2(t)) (x1(t)和x2(t)为输入信号，a和b为常数，L()表示对信号进行线性处理)2. 时不变性质: 若输入信号延时 T 后输出信号也延时 T，即 y(t) = L{x(t)}，则 y(t-T) = L{x(t-T)}3. 稳定性性质: 若输入信号 x(t) 有界，输出信号 y(t) 也有界，则系统是稳定的。

一、概述齐格勒-尼科尔斯（Ziegler-Nichols）是一种经典的单位阶跃响应曲线，用于控制系统的稳定性分析和参数整定。

这个方法是由美国工程师John G. Ziegler和Nathaniel B. Nichols于1942年提出的，是控制工程领域中非常重要的一部分。

本文将详细介绍齐格勒-尼科尔斯单位阶跃响应曲线的相关内容。

二、单位阶跃响应曲线基本概念1. 单位阶跃响应曲线的定义单位阶跃响应曲线是指在控制系统中输入单位阶跃信号时，系统的输出响应的曲线。

单位阶跃信号是在 t=0 时刻由零跃变成1的信号，其数学表示为u(t)=1, t>=0。

通过单位阶跃响应曲线可以分析系统的动态特性，对系统的稳定性和性能进行评估。

2. 单位阶跃响应曲线的特点单位阶跃响应曲线通常具有上升时间、峰值超调量、峰值时间等特征参数，这些参数可以从曲线上直接测量得到。

根据单位阶跃响应曲线的特点，可以得到系统的动态响应特性，从而进行控制器参数的整定。

三、齐格勒-尼科尔斯单位阶跃响应曲线的求解方法1. 基本思想齐格勒-尼科尔斯单位阶跃响应曲线的求解方法是根据系统的动态特性来确定控制器的参数。

其基本思想是通过改变控制器的增益和时间常数，使得系统的单位阶跃响应曲线能够达到某种特定的性能要求，如快速响应、稳定性等。

2. 求解步骤齐格勒-尼科尔斯单位阶跃响应曲线的求解步骤一般包括以下几个步骤：（1）确定系统的传递函数形式；（2）选择合适的控制策略，如比例控制、积分控制、比例积分控制等；（3）通过试控制法或者模拟仿真法，找到系统的临界增益和临界频率，从而确定控制器的参数。

四、齐格勒-尼科尔斯单位阶跃响应曲线的应用1. 控制系统整定齐格勒-尼科尔斯单位阶跃响应曲线常常被用于控制系统的参数整定。

通过分析单位阶跃响应曲线的特性参数，可以确定合适的控制器增益和时间常数，从而使得系统达到理想的动态响应性能。

2. 稳定性分析对于控制系统的稳定性分析，通过观察单位阶跃响应曲线的振荡频率和振荡幅度，可以对系统的稳定性进行初步判断，并确定合适的控制器参数。

阶跃响应与传递函数的关系一、引言阶跃响应与传递函数是控制系统理论中的两个重要概念，它们之间存在密切的关系。

在控制系统设计和分析中，我们需要了解这两个概念之间的联系和作用，以便更好地应用于实际问题。

本文将详细介绍阶跃响应与传递函数的关系。

二、阶跃响应的定义阶跃信号是一种特殊的输入信号，其形式为单位阶跃函数。

单位阶跃函数是一种从0瞬间跳变到1的函数，数学表达式为：u(t) = 0, t < 0u(t) = 1, t >= 0控制系统对于单位阶跃输入信号的输出称为阶跃响应。

在时域上，阶跃响应通常表示为y(t)，其数学表达式为：y(t) = Kp + Kd * (d/dt)y(t) + Ki * ∫y(t)dt其中Kp、Kd、Ki分别表示比例、微分和积分控制器的增益。

三、传递函数的定义传递函数是描述线性时不变系统（LTI）行为特征的重要工具，在控制系统理论中广泛应用。

传递函数通常表示为H(s)，其中s是复变量，表示系统的拉普拉斯变换。

传递函数描述了输入信号与输出信号之间的关系，其数学表达式为：H(s) = Y(s)/U(s)其中Y(s)和U(s)分别表示系统的输出和输入信号的拉普拉斯变换。

四、阶跃响应与传递函数的关系在控制系统中，阶跃响应与传递函数之间存在密切的关系。

具体来说，阶跃响应是传递函数在时域上的表现形式。

我们可以通过传递函数求解系统的阶跃响应。

1. 从传递函数求解阶跃响应对于一个线性时不变系统，其传递函数可以通过对系统进行拉普拉斯变换得到。

因此，我们可以通过对传递函数进行反演得到系统在时域上的表现形式，即阶跃响应。

具体来说，在s域中将传递函数H(s)除以s得到：H(s)/s = Y(s)/(U0 * s)其中U0表示单位阶跃输入信号的幅值。

将左右两边进行拉普拉斯反演得到：h(t) = L^{-1}[H(s)/s] = L^{-1}[Y(s)/(U0 * s)]其中L^{-1}表示拉普拉斯反演运算符。

单位阶跃函数是一个非常重要的信号函数，在工程数学中经常出现。

它的拉普拉斯变换式是一个非常重要的公式，在信号处理、控制系统等领域都具有重要的应用价值。

在本文中，我将详细解释单位阶跃函数的拉普拉斯变换式，以及其推导过程。

1. 单位阶跃函数的定义单位阶跃函数，通常用符号u(t)表示，其定义如下：u(t) = {0, t < 0;1, t > 0.}可以看出，单位阶跃函数在t = 0时取值为1，而在t < 0时取值为0。

2. 拉普拉斯变换的定义拉普拉斯变换是一种将一个函数f(t)转换为另一个函数F(s)的数学方法，其定义如下：F(s) = L{f(t)} = ∫[0, ∞] e^(-st) * f(t) dt其中，s是复变量，t是实变量，e^(-st)是指数函数。

3. 单位阶跃函数的拉普拉斯变换式现在我们来推导单位阶跃函数的拉普拉斯变换式。

根据拉普拉斯变换的定义，我们有：U(s) = L{u(t)} = ∫[0, ∞] e^(-st) * u(t) dt根据单位阶跃函数的定义，我们可以将积分区间分为两部分：U(s) = ∫[0, ∞] e^(-st) * u(t) dt = ∫[0, ∞] e^(-st) * dt= lim(t→∞) ∫[0, t] e^(-st) * dt= lim(t→∞) [-1/s * e^(-st)] [0, t]= lim(t→∞) [-1/s * (e^(-st) - 1)]当t→∞时，e^(-st)趋于0，因此上式等于：U(s) = lim(t→∞) [-1/s * (0 - 1)] = 1/s单位阶跃函数的拉普拉斯变换式为：U(s) = 1/s4. 结论单位阶跃函数的拉普拉斯变换式为U(s) = 1/s。

这个结论在信号处理、控制系统等领域有着广泛的应用，在分析系统的稳定性、频域特性等方面起着重要作用。

通过本文的讲解，我们对单位阶跃函数的拉普拉斯变换式有了更深入的理解，也了解了拉普拉斯变换的基本原理和推导过程。

阶跃信号与符号函数sgn(t)的关系阶跃信号是信号处理领域中常见的一种信号类型，它在某个特定的时间点突然变化，并在此后保持不变。

阶跃信号通常用符号函数sgn(t)来表示，它是一个以时间t为变量的函数。

符号函数sgn(t)的定义如下：sgn(t) = {-1, t < 00, t = 01, t > 0}可以看出，符号函数sgn(t)是根据时间t的正负来返回一个取值为-1、0或1的函数。

它在t=0时取值为0，当t > 0时取值为1，当t < 0时取值为-1。

阶跃信号与符号函数sgn(t)的关系在于，阶跃信号可以用符号函数sgn(t)来表示。

具体来说，我们可以将阶跃信号分为连续时间和离散时间两种情况进行讨论。

1.连续时间的阶跃信号：连续时间的阶跃信号通常用单位阶跃函数u(t)或者海维赛德函数H(t)来表示，它们与符号函数sgn(t)的关系如下：u(t) = (sgn(t) + 1) / 2H(t) = (sgn(t) + 1) / 2其中，u(t)表示单位阶跃函数，H(t)表示海维赛德函数。

它们都可以看作是符号函数sgn(t)的平移和缩放变换。

这种表示方式在信号处理领域中非常常见，并且更容易进行数学分析和计算。

2.离散时间的阶跃信号：离散时间的阶跃信号通常用序列的形式来表示，例如：x(n) = {0, n < 01, n >= 0}其中，x(n)表示离散时间的阶跃信号。

可以看出，它与符号函数sgn(t)的取值是一致的。

当n < 0时，x(n)的取值为0；当n >= 0时，x(n)的取值为1。

因此，离散时间的阶跃信号可以看作是符号函数sgn(t)在离散时间下的等价表示。

阶跃信号在信号处理领域中应用非常广泛。

它常常用于系统的输入信号，以模拟系统在某个时间点上的突变行为。

在实际应用中，可以通过控制信号的起始时间和幅值来改变阶跃信号的具体形状。

除了阶跃信号，符号函数sgn(t)还可以与其他信号类型进行组合，产生更复杂的信号形式。

阶跃信号尺度变换公式阶跃信号是一种特殊的信号，其在某一时间点突然从一个值跳变到另一个值。

在信号处理领域中，我们经常需要对信号进行尺度变换，即改变信号的幅度大小。

阶跃信号的尺度变换公式是一种常用的数学公式，用于描述阶跃信号在尺度变换后的形式。

阶跃信号的数学表达式是一个单位阶跃函数，通常表示为u(t)，其中t表示时间。

当t大于等于0时，u(t)的值为1；当t小于0时，u(t)的值为0。

阶跃信号的尺度变换公式可以表示为：y(t) = A * u(t)其中，y(t)表示尺度变换后的阶跃信号，A表示尺度变换的比例因子。

尺度变换公式中的乘法运算表示将原始信号的幅度乘以比例因子，从而得到尺度变换后的信号。

尺度变换公式的应用非常广泛。

在信号处理中，我们经常需要对信号进行放大或缩小操作，以便更好地进行分析和处理。

通过改变比例因子A的值，我们可以实现对信号的尺度变换。

当A大于1时，信号被放大；当A小于1时，信号被缩小。

尺度变换公式还可以用于描述信号的平移操作。

通过将尺度变换公式中的t替换为t-t0，其中t0表示平移的时间偏移量，我们可以实现对信号的平移操作。

平移操作将信号的整体形态沿时间轴平移，而不改变信号的幅度大小。

除了阶跃信号，尺度变换公式还可以应用于其他类型的信号，如方波信号、正弦信号等。

对于这些信号，尺度变换公式的形式也是类似的，只是具体的数学表达式会有所不同。

在实际应用中，尺度变换公式常常与其他信号处理技术相结合，如滤波、采样、编码等。

通过将尺度变换与这些技术相结合，我们可以实现更复杂的信号处理操作，从而满足不同应用的需求。

阶跃信号尺度变换公式是一种常用的数学工具，用于描述信号在尺度变换后的形式。

通过改变比例因子A的值，我们可以实现对信号的放大或缩小操作，从而适应不同的信号处理需求。

尺度变换公式在信号处理领域具有广泛的应用，是我们理解和分析信号行为的重要工具。