医学统计学讲义第十章线性相关
- 格式：ppt
- 大小：476.50 KB
- 文档页数：53
下载文档原格式
合集下载
医学统计学简单线性回归和线性相关
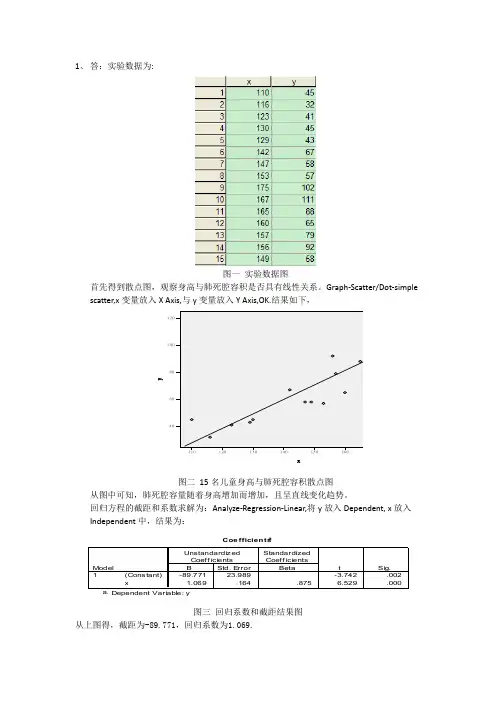
1、答：实验数据为:图一实验数据图首先得到散点图，观察身高与肺死腔容积是否具有线性关系。
Graph-Scatter/Dot-simple scatter,x图二15名儿童身高与肺死腔容积散点图从图中可知，肺死腔容量随着身高增加而增加，且呈直线变化趋势。
回归方程的截距和系数求解为：Analyze-Regression-Linear,将y放入Dependent, x放入Independent中，结果为：图三回归系数和截距结果图从上图得，截距为-89.771，回归系数为1.069.回归系数等于0的假设检验：建立假设、确定检验水准α。
H0:β=0,即儿童的身高与肺死腔容积无直线关系。
H1:β≠0,即儿童的身高与肺死腔容积有直线关系。
检验水准α=0.05计算检验统计量F值，确定P值。
图四方差齐性结果图从上图得，F=42.629，概率P<0.05，即拒绝H0,接受H1，可认为儿童的身高与肺死腔容积有直线关系。
证明：由图三和图四可得，t b=6.529=√F=6.529。
估计回归系数的95%置信区间：Analuze-Regression-Linear-save，勾上Mean，结果如下,图五总体回归系数置信区间得总体回归系数95%置信区间为(13.664,109.797)。
2、答：实验数据为：图一实验数据图首先得到散点图，观察凝血时间与凝血酶浓度是否具有线性关系。
Graph-Scatter/Dot-simple scatter,x变量放入X Axis,与y变量放入Y Axis,OK.结果如下，图二15名健康成人凝血时间与凝血酶浓度散点图从图中可知，凝血酶浓度随着凝血时间增加而减少，且呈直线变化趋势。
其次进行双变量正态检验：对x进行正态检验，结果为，图三 x变量正态检验结果图从上图可知，概率P>0.05，即x变量服从正态变量。
以凝血酶浓度和凝血时间作直线回归，并进行残差分析。
Analyze-Regression-Linear,将y放入Dependent, x放入Independent中，结果为：图四回归系数和截距结果图从上图得，截距为2.816，回归系数为-0.123.并且从上图得，概率P<0.05，即拒绝H0,接受H1，可认为凝血时间与凝血酶浓度有直线关系。
医学统计学-直线相关和回归分析
Page 6
2.相关的概念
➢当两个数值变量之间出现如下情况：当一个 变量增大，另一个也随之增大(或减少)，我 们称这种现象为共变，也就是有相关关系。
➢若两个变量同时增加或减少，变化趋势是同 向的，则两变量之间的关系为正相关 (positive correlation)；若一个变量增加时，另 一个变量减少，变化趋势是反向的，则称为 负相关(negative correlation)。
Page 17
➢H0：ρ＝0，两变量间无直线相关的关系；
➢H1：ρ≠0，两变量间有直线相关的关系；
➢a =0.05
t 0.9456 7.1196 1 0.94562
82
➢ν=8-2=6
➢以自由度为6查附表2的t界值表，得P<0.01， 按α=0.05的水准拒绝H0，接受H1，认为2岁 时的身高和成年身高之间存在正相关。
)
XY X Y / X 2 X 2 / n
n
lXY lXX
a Y bX
Page 41
最小二乘法求解(了解)
Q (Y Yˆ )2 (Y a bX )2 最小
根据微积分学中的求极值的方法，令 Q对a、
b的一阶偏导数等于0，即：
Q
a
n
2
i 1
Yi
a
bX i
0
Q b
n
2
i 1
Yi
Page 7
直线相关的概念
➢直线相关（linear correlation），又称简单相 关，用以描述两个呈正态分布的变量之间的 线性共变关系，常简称为相关。
Page 8
➢用以说明具有直线关系的两个变量间相关关 系的密切程度和相关方向的指标，称为相关 系数（correlation coefficient），又称为积差 相关系数（coefficient of product-moment correlation），Pearson相关系数 。
2.相关的概念
➢当两个数值变量之间出现如下情况：当一个 变量增大，另一个也随之增大(或减少)，我 们称这种现象为共变，也就是有相关关系。
➢若两个变量同时增加或减少，变化趋势是同 向的，则两变量之间的关系为正相关 (positive correlation)；若一个变量增加时，另 一个变量减少，变化趋势是反向的，则称为 负相关(negative correlation)。
Page 17
➢H0：ρ＝0，两变量间无直线相关的关系；
➢H1：ρ≠0，两变量间有直线相关的关系；
➢a =0.05
t 0.9456 7.1196 1 0.94562
82
➢ν=8-2=6
➢以自由度为6查附表2的t界值表，得P<0.01， 按α=0.05的水准拒绝H0，接受H1，认为2岁 时的身高和成年身高之间存在正相关。
)
XY X Y / X 2 X 2 / n
n
lXY lXX
a Y bX
Page 41
最小二乘法求解(了解)
Q (Y Yˆ )2 (Y a bX )2 最小
根据微积分学中的求极值的方法，令 Q对a、
b的一阶偏导数等于0，即：
Q
a
n
2
i 1
Yi
a
bX i
0
Q b
n
2
i 1
Yi
Page 7
直线相关的概念
➢直线相关（linear correlation），又称简单相 关，用以描述两个呈正态分布的变量之间的 线性共变关系，常简称为相关。
Page 8
➢用以说明具有直线关系的两个变量间相关关 系的密切程度和相关方向的指标，称为相关 系数（correlation coefficient），又称为积差 相关系数（coefficient of product-moment correlation），Pearson相关系数 。
医学统计学 10第十讲 线性相关
2
XX
X2
X2
n
lYY
2
Y Y
Y2
Y2
n
l XY
X
X Y
Y
XY
X Y
nቤተ መጻሕፍቲ ባይዱ
例13-1
测得某地15名正常成年人的血铅X和24小 时的尿铅Y，试分析血铅与24小时尿铅之 间是否直线相关。
15名自愿者的血铅和24小时尿铅测量值（μmol/L）
编号 X
Y 编号 X
Y
1 0.11 0.14 9 0.23 0.24
∑X=3.00 ∑Y=3.17 ∑ X2=0.7168 ∑Y2=0.7681 ∑XY=0.7388 n=15
=0.9787
相关系数的假设检验
上例中的相关系数r等于0.9787，说明了15例样本中血 铅与尿铅之间存在相关关系。但是，这15例只是总体中的 一个样本，由此得到的相关系数会存在抽样误差。因为，总 体相关系数（）为零时，由于抽样误差，从总体抽出的15 例，其r可能不等于零。所以，要判断该样本的r是否有意义， 需与总体相关系数=0进行比较，看两者的差别有无统计学 意义。这就要对r进行假设检验，判断r不等于零是由于抽样 误差所致，还是两个变量之间确实存在相关关系。
2 0.25 0.25 10 0.33 0.30
3 0.23 0.28 11 0.15 0.16
4 0.24 0.25 12 0.04 0.05
5 0.26 0.28 13 0.20 0.20
6 0.09 0.10 14 0.34 0.32
7 0.25 0.27 15 0.22 0.24
8 0.06 0.09
习题
1.相关分析一般是研究（ ） A.两份随机样本的两个相同指标的相互关系 B.两份随机样本的两个相同指标间的差别 C.两份随机样本的两个不同指标的相互关系 D.一份随机样本的两个相同指标的相互关系 E.一份随机样本的两个不同指标的相互关系 2.相关系数反映了两变量间的（ ） A.依存关系 B.函数关系 C.比例关系 D.相关关系 E.因果关系
医学统计学直线相关
23
6.
相关分析应用时，区别两点
¾ 假设检验结果，说明相关关系的可靠程度。 ¾ |r|值的大小：说明相关关系的密切程度
7.
两个样本能否合并为一个样本后再进行相 关分析，应审慎对待。
24
等 级 相关
Rank Correlation
等级相关一般概念
等级相关相当于秩相关，是一种非参数方
法，即以秩次取代原始数据的分析方法。 适用如下列资料：
u = rs n − 1
ν =∞
29
例：用60Co对狗造成急性放射病，对照
射后5天时的健康状况进行综合评分，并 记录其存活天数，见表7-3第⑵、⑷栏。 试作等级相关分析。
30
等级相关系数计算表
编号 1 2 3 4 5 6 7 合计 综合评分 X Ui 79 2 80 3 91 6 90 5 70 1 87 4 92 7 存活天数 Y Vi >45 7 30 6 16 2 24 3 28 5 25 4 14 1 d -5 -3 4 2 -4 0 6 d2 25 9 16 4 16 0 36 106
17
两种假设检验方法
按ν=n-2直接查附表13（r界值表），确定P 值。相同自由度下，r值越大，P值越小。 t 检验：
r −0 r t= = s r 1− r 2 n −2
ν=n-2，根据t值和ν查t界值表。
18
例：就上例所得r值，检验TcPO2与PaO2之间是 否存在直线关系？ H0：两变量之间不存在直线相关关系，ρ =0 H1： ρ >0 单侧α =0.05 本例，n=10，r=0.844，则
31
H0: 健康状况综合评分与生存时间不存在 相关关系（ρs＝0） H1: 健康状况综合评分与生存时间存在相 关关系（ρs≠0）
6.
相关分析应用时，区别两点
¾ 假设检验结果，说明相关关系的可靠程度。 ¾ |r|值的大小：说明相关关系的密切程度
7.
两个样本能否合并为一个样本后再进行相 关分析，应审慎对待。
24
等 级 相关
Rank Correlation
等级相关一般概念
等级相关相当于秩相关，是一种非参数方
法，即以秩次取代原始数据的分析方法。 适用如下列资料：
u = rs n − 1
ν =∞
29
例：用60Co对狗造成急性放射病，对照
射后5天时的健康状况进行综合评分，并 记录其存活天数，见表7-3第⑵、⑷栏。 试作等级相关分析。
30
等级相关系数计算表
编号 1 2 3 4 5 6 7 合计 综合评分 X Ui 79 2 80 3 91 6 90 5 70 1 87 4 92 7 存活天数 Y Vi >45 7 30 6 16 2 24 3 28 5 25 4 14 1 d -5 -3 4 2 -4 0 6 d2 25 9 16 4 16 0 36 106
17
两种假设检验方法
按ν=n-2直接查附表13（r界值表），确定P 值。相同自由度下，r值越大，P值越小。 t 检验：
r −0 r t= = s r 1− r 2 n −2
ν=n-2，根据t值和ν查t界值表。
18
例：就上例所得r值，检验TcPO2与PaO2之间是 否存在直线关系？ H0：两变量之间不存在直线相关关系，ρ =0 H1： ρ >0 单侧α =0.05 本例，n=10，r=0.844，则
31
H0: 健康状况综合评分与生存时间不存在 相关关系（ρs＝0） H1: 健康状况综合评分与生存时间存在相 关关系（ρs≠0）
医学统计学(课件)线性相关与回归
• X-自变量（independent variable）；
• Y-应变量（dependent variable）；
•
Y
-
给定cept）或常数项（constant term）；
• b - 回归系数（regression coefficient）。
回归方程参数的计算
表11-2 方差分析表
变异来源 SS
MS
F
总变异 14563.13
8
回归
12538.06
1
12538.06 43.34
残差
2025.07
7
289.30
P
<0.01
Hypothesis test
（二） t 检验
b0 t
Sb
Sb
SY X l XX
n2
SY X
SS残差
残差
lYY
(Y Y )2
Y 2 ( Y )2 n
• 例11-2 从男青年总体中随机抽取11名男青年组成 样本，分别测量每个男青年的身高和前臂长，测
量结果如表11-3所示，试计算身高与前臂长之间
的相关系数。
52
50
48
前臂长(cm)
46
44
42
40
150
160
170
180
190
则回归方程为：
Yˆ 13.049 9.94X
simple regression
（3）作回归直线
• 按上述回归方程，在 X 实测值的范围内，任取两个 相距较远的点 A( X1 ,Yˆ1 ) 和 B( X2 ,Yˆ2 )，连接A、B两点 即得到回归直线。
医学统计学相关线性回归
医学统计学相关线性回归
通过本次演讲，我们将深入讨论医学统计学中与线性回归相关的课题，从介 绍线性回归的概念和应用开始，逐步深入到模型、方法和实践案例等方面。
什么是线性回归？
线性回归是一种用来研究自变量与因变量间关系的统计方法。通过拟合线性模型，我们能够对变量间的 关系进行建模、预测和解释。
线性回归的应用
线性回归的优化算法
为了拟合最佳的回归模型，我们可以使用不同的优化算法，如梯度下降、牛 顿法和拟牛顿法等。
广义线性模型
广义线性模型是线性回归的扩展，通过引入链接函数和指数族分布，可以处 理因变量不满足正态分布的情况。
残差分析
残差分析用于评估模型的拟合优度和残差的性质。正常的残差应当满足独立性、无明显的模式和符合正 态分布。
反应曲面法
反应曲面法可以帮助我们更好地理解自变量与因变量的关系。通过绘制反应 曲面图，我们可以可视化预测结果和优化因素。
最小二乘法
最小二乘法是一种常用的线性回归系数估计方法，通过最小化观测值与模型预测值之间的差异来拟合最 佳拟合直线或平面。
岭回归、Lasso回归和Elastic Net回归
岭回归通过L2正则化项控制回归系数的大小；Lasso回归通过L1正则化项使得 某些回归系数为零；Elastic Net回归结合了L2和L1正则化项的优势。
正则化回归的优缺点
1 优点
减少多重共线性和过拟合的影响，提高模型预测性能。
2 缺点
模型复杂度提高，对解释性较弱。
参数估计
参数估计用于计算回归系数的值，帮助我们理解自变量对因变量的影响大小 和方向。
量影响分析
量影响分析用于衡量自变量对因变量的影响程度。通过变化自变量的取值，我们可以观察因变量的变动 情况。
通过本次演讲，我们将深入讨论医学统计学中与线性回归相关的课题，从介 绍线性回归的概念和应用开始，逐步深入到模型、方法和实践案例等方面。
什么是线性回归？
线性回归是一种用来研究自变量与因变量间关系的统计方法。通过拟合线性模型，我们能够对变量间的 关系进行建模、预测和解释。
线性回归的应用
线性回归的优化算法
为了拟合最佳的回归模型，我们可以使用不同的优化算法，如梯度下降、牛 顿法和拟牛顿法等。
广义线性模型
广义线性模型是线性回归的扩展，通过引入链接函数和指数族分布，可以处 理因变量不满足正态分布的情况。
残差分析
残差分析用于评估模型的拟合优度和残差的性质。正常的残差应当满足独立性、无明显的模式和符合正 态分布。
反应曲面法
反应曲面法可以帮助我们更好地理解自变量与因变量的关系。通过绘制反应 曲面图，我们可以可视化预测结果和优化因素。
最小二乘法
最小二乘法是一种常用的线性回归系数估计方法，通过最小化观测值与模型预测值之间的差异来拟合最 佳拟合直线或平面。
岭回归、Lasso回归和Elastic Net回归
岭回归通过L2正则化项控制回归系数的大小；Lasso回归通过L1正则化项使得 某些回归系数为零；Elastic Net回归结合了L2和L1正则化项的优势。
正则化回归的优缺点
1 优点
减少多重共线性和过拟合的影响，提高模型预测性能。
2 缺点
模型复杂度提高，对解释性较弱。
参数估计
参数估计用于计算回归系数的值，帮助我们理解自变量对因变量的影响大小 和方向。
量影响分析
量影响分析用于衡量自变量对因变量的影响程度。通过变化自变量的取值，我们可以观察因变量的变动 情况。
第十章 线性相关与回归
相关与回归
28
直线回归就是用来研究两个连续性变量x 直线回归就是用来研究两个连续性变量 之间的数量依存关系。 和y之间的数量依存关系。其中 为自变 之间的数量依存关系 其中x为自变 y为因变量 它依赖于x。 为因变量， 量，y为因变量，它依赖于x。 直线回归适用于单变量正态分布资料， 直线回归适用于单变量正态分布资料，即 y为随机正态变量，x为可以精确测量的 为随机正态变量， 为可以精确测量的 为随机正态变量 值。
31
根据上例的数据，求男青年身高与前臂长之间的回归 方程。 从相关系数的计算中，已经求得：
• • • • • • ∑X=1891 ∑Y=500 ∑ X2=89599 ∑ Y2=22810 ∑XY=86185 N=11
相关与回归 12
例 10.1
• 从男青年总体中随机抽取11名男青年的身 高和前臂长，身高和前臂长均以cm为单位， 测量结果如表10-1所示，试计算身高与前 臂长之间的相关系数？是正相关还是负相 关？
相关与回归
13
表10-1 11例男青年身高与前臂长的测量结果 例男青年身高与前臂长的测量结果
编号 1 2 3 4 5 6 7 8 9 10 11 身高（cm） 170 173 160 155 173 188 178 183 180 165 166 前臂长（cm） 47 42 44 41 47 50 47 46 46 43 44
X、Y 变化趋势相同---变化趋势相同---完全正相关; 完全正相关; 反向变化----完全负相关。 反向变化----完全负相关。 ----完全负相关
图12-3 12相关系数示意图
相关与回归
9
X、Y 变化互不影响----零 变化互不影响-------零
相关(zero 相关(zero correlation)
医学统计学直线相关与回归分析
SY|X为Y的剩余标准差——扣除X的影响后Y的变异程度。
SY|X
Y Yˆ 2
n2
残差 2
＝ n2
SS剩 ＝ n2
MS剩＝ˆY|X
Y的剩余标准差——扣除X的影 响后Y （即回归所能解释的部 分）本身的变异程度
SY|X 度量了实际散点远离回归直线的离散程度， 反映了模型的可靠性。越小模型越好。
直线回归系数的t检验
H0：总体回归系数＝0； H1：总体回归系数≠0； =0.05
=15-2=13
按=13查t界值表，t0.05/2,13=2.160， t0.01/2,13=3.012， t>t0.01/2,13，得P<0.01。按 =0.05水准拒绝H0，接受H1。
认为胰岛素和血糖存在直线回归关系。
直线相关与回归
Linear Correlation and regression Analysis
▪ 人的体重往往随着身高的增加而增加。二 者之间是否存在某种关联？如果存在，可 否用身高来推测体重的多少？
▪ 人的肺活量往往随着胸围的增加而增加。 是否可以建立胸围和肺活量的数量关系？
▪ 还有：年龄与血压、药物剂量与动物死亡 率、胰岛素与血糖水平的关系等
可以用回归来解释的部分
Y即的与X有总关变的部异分
份额的大小可以 用相关系数的平
方来衡量 （决定系数）
不能用X来解释的部分 即与X无关的部分（随机误差）
Page 72
估计值 的意义
▪ 给定X时，Y的均数的估计值。 ▪ X=10, = 12.7015
即胰岛素为10mU/L，平均血糖值为 12.7015mmol/L
15例糖尿病患者胰岛素患者胰岛素水平和血糖水平的散点图
第10章 线性相关与回归818
1.正相关 2.负相关 3.无相关
二、线性相关系数
相关系数就是说明具有直线关系的两个变量间相关密切 程度和相关方向的统计量。
皮尔森(Pearson)相关系数的计算公式为：
r
r rXY
( X X )(Y Y ) LXY
( Xi X )2 (Yi Y )2
LXX .LYY
相关系数r没有测量单位，其数值为-1≤r≤1
400
1156
33
726
484
1089
246
3622
2024
6610
根据表10-2数据绘制散点图，如下图所示：
40
30
蛙心律
20
Yˆ 4.087 1.523X
10
0
0
10
20
30
温度
三、线性回归方程的显著性检验
对线性回归方程要进行假设检验，就是要检验b是否 为β=0的总体中的一个随机样本。该假设检验通常 用采用方差分析或者t检验，两者的检验效果等价。
医学统计学
第十章 线性相关与回归
房价走势图
模拟数据
症状监测图
模拟数据
一、线性相关的基本概念
把这种Y随着X变化而变化的关系称之为相关关系，如果这种变 化呈现直线关系，又称之为直线相关（线性相关）或简单相关。
相关关系 直线相关
根据散点图中点的分布即线性相关的性质和相关之间的密 切程度，可分为以下几种情况：
t检验： t | b 0 | , =n-2
sb
方差分析： SS总 SS回归 SS剩余，总 =回归 +剩余
MS回归
SS回归
回归
，MS剩余
SS剩余 ，F
剩余
MS回归 MS剩余
二、线性相关系数
相关系数就是说明具有直线关系的两个变量间相关密切 程度和相关方向的统计量。
皮尔森(Pearson)相关系数的计算公式为：
r
r rXY
( X X )(Y Y ) LXY
( Xi X )2 (Yi Y )2
LXX .LYY
相关系数r没有测量单位，其数值为-1≤r≤1
400
1156
33
726
484
1089
246
3622
2024
6610
根据表10-2数据绘制散点图，如下图所示：
40
30
蛙心律
20
Yˆ 4.087 1.523X
10
0
0
10
20
30
温度
三、线性回归方程的显著性检验
对线性回归方程要进行假设检验，就是要检验b是否 为β=0的总体中的一个随机样本。该假设检验通常 用采用方差分析或者t检验，两者的检验效果等价。
医学统计学
第十章 线性相关与回归
房价走势图
模拟数据
症状监测图
模拟数据
一、线性相关的基本概念
把这种Y随着X变化而变化的关系称之为相关关系，如果这种变 化呈现直线关系，又称之为直线相关（线性相关）或简单相关。
相关关系 直线相关
根据散点图中点的分布即线性相关的性质和相关之间的密 切程度，可分为以下几种情况：
t检验： t | b 0 | , =n-2
sb
方差分析： SS总 SS回归 SS剩余，总 =回归 +剩余
MS回归
SS回归
回归
，MS剩余
SS剩余 ，F
剩余
MS回归 MS剩余
医学统计人卫线性相关与回归
➢S S 回 为 回 归 平 方 和 ， 它 反 映 在 Y 的 总 变 异 中 由 于 X 与 Y的直线关系而使Y变异减小的部分，也就是在总平
方和中可以用X解释的部分。SS回越大，说明回归效 果越好,即SS总中可用X与Y线性关系解释的变异越多。
➢S S 剩 为 剩 余 平 方 和 ， 它 反 映 X 对 Y 的 线 性 影 响 之 外 的 一切因素对Y的变异的作用，也就是在总平方和SS总 中无法用X解释的部分。在散点图中，各实测点离回
1.两变量的变化趋势呈直线趋势(linear)； 2.因变量y属于正态随机变量(normal distribution)；
x y 3.对于I型回归要求对于每个选定的 ， 都有一个正态分布的总体，并且这些总 x y 体的方差都相等(equal variance)；对于II型回归，要求 、 均服从正态
分布。
3.两变量间存在直线相关关系，并不一定是因果 关系，可能是伴随关系；
4.直线回归方程的适用范围一般以自变量的取值
范围为限，在此范围内求出的估计值称内插；
超此范围所得Ŷ称外延。若无充分理由应避免
外延。
第25页/共29页
直线相关与回归的区别与联系
（一）区别
1. 资料要求不同：相关要求两个变量是双变量正 态分布；回归要求应变量Y服从正态分布，而自 变量X是能精确测量和严格控制的变量。
3.利用回归方程进行统计控制：规定Y值的变化，通过控制X的范围来实现统计 控制的目标,所以统计控制是利用回归方程进行的逆估计。
第24页/共29页
应用直线相关和回归应注意的问题
1.作直线相关和回归分析要有实际意义；
2.在进行分析之前，应先绘制散点图，当其分布 有直线趋势时，才适宜作直线相关回归分析。 散点图还能提示资料有无异常点。
医学统计学第十章线性相关
3 选择合适的方法
根据变量的类型和相关性 的形态选择合适的相关系 数计算方法。
偏相关系数的计算方法
控制其他变量
偏相关系数可以通过计算两个变 量在控制其他变量影响下的相关 性得出。
计算公式
偏相关系数的计算需要考虑各个 变量的相关系数和协方差。
解读结果
偏相关系数的值可以告诉我们， 在控制其他变量的情况下，感兴 趣变量之间的纯粹相学统计学中的重要概念之一，它描述了变量之间的关系。本章 将介绍线性相关的定义、分析方法和计算公式，并探讨相关系数的性质和显 著性检验。
散点图的分析方法
Visualizing Relationships
使用散点图可以直观地展示变 量之间的关系，通过观察点的 分布和走势，可以初步判断是 否存在线性相关。
用于衡量线性相关的强度和方向，取值范围为-1到1，绝对值越接近1，相关性越强。
Spearman 相关系数
用于衡量变量之间的单调关系，不受线性假设的限制，适用于有序和无序数据。
偏相关系数
用于控制一个或多个变量的影响，测量剩余变量与感兴趣变量之间的相关性。
相关系数的性质
1
正相关
当变量之间存在正相关时，它们的值会同时增加或减少。
Identifying Outliers Exploring Patterns
散点图还可以帮助我们识别异 常值，即偏离正常关系的数据 点，这对于后续的分析和处理 非常重要。
通过散点图，我们可以发现各 种有趣的模式和趋势，这有助 于深入了解变量之间的关系。
相关系数的计算公式
Pearso n 相关系数
2
负相关
当变量之间存在负相关时，一个变量的增加会导致另一个变量的减少。
3
医学统计学相关线性回归
由X推算Y的方程： X ax. y bx. yY
由Y推算X的方程： Y a y.x by.x X
2、应用不同：说明两变量间依存变化的数量关系 用回归，说明变量间的相关关系用相关。
3、意义不同：b表示X每增（减）一个单位，Y平 均改变b个单位；r说明具有直线关系的两个变量间 相关关系的密切程度与相关的方向。
判断回归方程效果的指标: 1、剩余标准差 2、残差 3、决定系数
P444
回归分析的一般步骤： 1. 绘制散点图，初步判断是否呈直线
趋势
2.计算a、b。(如果基本呈直线趋势)
3.对b作假设检验
方法： (1) F检验 (2) t检验 (3) 用r检验来代替。
4.作结论
如P≤0.05, 说明方程成立，列出回归方程； 如P >0.05, 说明方程不成立，不列回归 方程。
Unstandardized Standardized Adjusted S.E of mean predictions
应变量原始预测值
标准化后的预测值，预测值的均数为0， 标准差为1
不考虑当前记录，当前模型对该记录应 变量的预测值
预测值的标准差
Mean
条件均数的置信区间
Individual 个体 y 值的容许区间
散点呈随机分布，
斜率为0，说明误差项独 立，独立性假设成立。
不能直接采用 直线回归分析。
体重与学生化残差散点图
由X推Y的回归方程为： Y=-58.235+0.716X
相关分析的一般步骤： 1.绘制散点图 2.求r 3. 对r作假设检验: (1) t检验; (2) 查表 4.作结论：有无相关及其方向
输出系列相关残差的Durbin-Watson检验和残差与预测值
医学统计学第十章线性相关
n
lYY
2
YY
Y2
Y2
n
lX Y X X Y Y X Y X n Y
相关系数的性质
总体相关系数
-1 ≤ r ≤ 1 r＞0为正相关 r＜0为负相关 r＝0为零相关或无相关
相关关系示意图
0≤ rC ≤ 1
例10.5 两种血型系统的相关性
某人按两种血型系统统计某地6094人的血型分布，结 果见表10.5，问两种血型的分布间有无关系？
ABO 血型 M
O 431 A 388 B 495 AB 137 合计 1451
MN血型 N MN
490 902 410 800 587 950 179 325 1666 2977
350
秒)
300 50
60
70
80
90
100
心率(次/分)
男
300
50
60
70
80
90
100
心率(次/分)
女
(2) 分别计算两样本相关系数r
男性
r1
14.3 23 7330.8827 85.686 6370.9 41 467
女性
r2
23.2 55 1 0.9179 13.9 31 8 6479.2 05 000
缩时间均呈负相关关系
(4)比较两总体相关系数是否相等
H0：男子心率与心脏左室电机械收缩时间的相
关与女子的相等，1＝2；
H1：男子心率与心脏左室电机械收缩时间的相
关与女子的不等，1≠2。 =0.10。
作z变换，然后对z值进行分析
z1 1 2 l n 1 1 0 0 ..8 88 8 2 2 -1 7 7.， 3z2 8 1 2 7 l n 1 1 9 0 0 ..9 91 1 7 7 -1 9 9.57
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相关系数的含义
表达两变量间线性相关的程度和方向的一个统 计指标
➢ 符号: 相关系数小于0为负相关；大于0为正相关； 等于0为零相关。 ➢ 数值: 相关系数的绝对值越大，表示两变量间的相 关程度越密切；相关系数越接近于0，表示相关越不密 切。
例10.1资料相关系数的计算
X ＝ 1.4 34 Y5.7266 lXX 2.9 404lY0Y 1.543lX 9Y 5.9396
r 5.9396 0.9579 2.4904 10 .5439
10.2.2 相关系数的假设检验
H 0：＝0，体重与体表面积无相关关系；
H 1：0，体重与体表面积有相关关系。
= 0.05
t r 0 sr
r 1r2 n2
t 服从自由度为n-2的 t 分布。
例10.1资料相关系数的假设检验
t r ＝ 0.9579 9.4369 1r2 10.95729
133.4 57.266
分析步骤
散点图 相关系数计算 相关系数的假设检验
10名3岁男童体重与体表面积散点图
体
6.5
表
面
积 6.0
Y
(103cm2)
5.5
5.0
11
12
13
14
15
16
体重(kg)，X
Pearson相关系数的计算
r
XXYY lXY
2
2
XX YY
lXlX YY
精品
医学统计学第十章线性相关
例:某医院欲研究儿童的体重与体表面积的关系，测
量了10名3岁男童体重与体表面积，数据见下表
编号
1 2 3 4 5 6 7 8 9 10 合计
X (X,kg)
11.0 11.8 12.0 12.3 13.1 13.7 14.4 14.9 15.2 16.0 133.4
Y (Y,103cm2)
圆的周长与半径的关系： C＝2R
速度、时间与路程的关系：L＝ST
X与Y的函数关系：
Y＝a+bX
非确定性关系：两变量在宏观上存在关系，但并未精 确到可以用函数关系来表达。
青少年身高与年龄的关系；
年龄与血脂的关系；身高与体重的关系；
体重与体表面积的关系；
药物浓度与反应率的关系；
相关关系与确定性关系(2)
0 01234
(f) z
z变换（双曲正切变换）
R.A.Fisher(1921)提出的
z 1 ln1 r 2 1 r
其反变换
r e2z 1 e2z 1
的区间估计
z值 的分布
变换值z近似服从均数为
1 2ln (1r)/1(r)
标准差为 1/ n的正3 态分布
将相关系数r变换为z值，并按正态分布原理估
当对事物的规律了解加深时，相关关系 可以转变为确定性关系。
父亲患白化病X, (X=是，否); 子女患白化病Y, (Y=是，否); X与Y的关系不确定。
当母亲患白化病时，X与Y的关系确定： X=是，则Y=是； X=否，则Y=否。
(父亲为异常基因的携带者出外。)
相关关系(correlation)
例10.1 10名3岁男童体重与体表面积的关系
编号 1 2 3 4 5 6 7 8 9
合计
体重(X,kg) 体表面积(Y,103cm2)
11.0 5.283 11.8 5.299 12.0 5.358 12.3 5.292 13.1 5.602 13.7 6.014 14.4 5.830 14.9 6.102 15.2 6.075 10 16.0 6.411
100
0 -1.0 -0.8 -0.6 -0.4 -0.2 0.0
= -0.8
=0
300
200
100
0 0 0.2 0.4 0.6 0.8 1.0
=0.8
.5 1.0 1.5 2.0
(d) z
200 150 100 50
0 -2 -1 0 1 2
(e) z
250 200 150 100 50
5.283 5.299 5.358 5.292 5.602 6.014 5.830 6.102 6.075 6.411 57.266
内容
相关关系与确定性关系 定量资料的相关 定性资料的相关 等级资料的相关 相关分析的正确应用
10.1 相关关系与确定性关系
确定性关系：两变量间的函数关系
r e2z 1 e2z 1
的95%可信区间：0.8271～0.9903； 的99%可信区间：0.7373～0.9939
10.2.4 两样本相关系数的比较
X 的离均差平方和:
2
lXX XX
Y 的离均差平方和:
2
lYY YY
X与Y 间的离均差积和: lX Y X X Y Y
离均差平方和、离均差积和的展开：
lXX
2
X X
X 2
X2
n
lYY
2
YY
Y2
Y2
n
lX Y X X Y Y X Y X n Y
当一个变量增大，另一个也随之增大 (或减少)，我们称这种现象为共变，或 相关(correlation)。两个变量有共变现 象，称为有相关关系。
相关关系不一定是因果关系。
10.2 定量资料的相关
反映两定量指标间的相关关系用 Pearson 相关系数。 (Pearson correlation coefficient)
相关系数的性质
总体相关系数
-1 ≤ r ≤ 1 r＞0为正相关 r＜0为负相关 r＝0为零相关或无相关
相关关系示意图
正相关
负相关
零相关
零相关
0<r<1 (a)
完全正相关
-1<r<0 (c)
完全负相关
r0 (e)
零相关
r0 (g)
零相关
r＝1
r＝-1
r＝0
r=0
(b)
(d)
(f)
(h)
计z的 100(1- )%的可信限
zusz zu
1 n3
然后再进行反变换，求出的可信区间
以例10.1数据为例，试计算总体相关系数
的95%及99%可信区间 z的95%可信区间：
1.9198±1.96×0.3780 = (1.1789，2.6607) z的99%可信区间：
1.9198±2.58×0.3780 = (0.9446，2.8950)
n2
102
自由度＝10－2，P＜0.001
拒绝H0，接受H1。可以认为3岁男童体重与体
表面积之间有正相关关系。
10.2.3 总体相关系数的区间估计
相关系数 分布
相关系数 =0
样本相关系数的分布是对称的，当样本含量较大时，近 似正态分布
相关系数不等于0
样本相关系数的分布是偏态
300
200