COS 目录

1.1 缩略语和符号表示以下缩略语和符号表示适用于本手册：AID ：应用标识符（Application Identifier）APDU ：应用协议数据单元（Application Protocol Data Unit）ATR : 复位应答（Answer to Reset）b ：二进制（Binary）BER : 基本编码规则（Basic Encoding Rules）BWI : 块等待时间整数（Block Waiting Time Integer）CLA : 命令报文的类别字节（Class Byte of the Command Message）CWI : 字符等待时间整数（Character Waiting Time Integer）DEA : 数据加密算法（Data Encryption Algorithm）DES : 数据加密标准（Data Encryption Satandard）DF : 专用文件（Dedicated File）DIR : 目录（Directory）ED ：电子存折（Electronic Deposit）EDC : 错误检测代码（Error Detection Code）EF : 基本文件（Elementary File）EMV : Europay、Mastercard、VISAEP ：电子钱包（Electronic Purse）Etu ：基本时间单元（Elementary Time Unit）FCI : 文件控制信息（File Control Information）FID ：文件标识（File Identifier）GND : 地（Ground）Hex. ：十六进制数（Hexadecimal）IC : 集成电路（Integrated Circuit）ICC ：集成电路卡（Integrated Circuit Card）IEC : 国际电工委员会（International Electrotechnical Commission）INS : 命令的指令字节（Instruction Byte of Command Message）ISO : 国际标准化组织（International Standardization Organization）Lc : 终端发出的命令数据域的实际长度Le : 响应数据的最大期望长度LEN ：长度（Length）MAC ：报文鉴别代码（Message Authentication Code）MF : 主控文件（Master File）P1 : 参数1（Parameter 1）P2 : 参数2（Parameter 2）PBOC : 中国人民银行PIN : 个人密码（Personal Identification Number）PIX : 专用应用标识符扩展码（Proprietary Application Identifier Extension) PSA : 支付系统应用（Payment System Application）PSAM ：消费安全存取模块（Purchase Secure Access Module）PSE : 支付系统环境（Payment System Environment）RFU ：保留为将来使用（Reserved for Future Use）RID : 已注册的应用提供者标识（Registered Application Provider Identify) RST : 复位（Reset）SAM ：安全存取模块（Secure Access Module）SFI : 短文件标识符（Short File Identifier）SW1 : 状态码1（Status Word One）SW2 : 状态码2（Status Word Two）TAC : 交易认证码（Transaction Authorization Crypogram）TCK : 校验字符（Check Character）TLV : 标签、长度、值（Tag Length Value）VCC : 电源电压（Supply Voltage）VPP : 编程电压（Programming Voltage）‘0’～‘9’和‘A’～‘F’：十六进制数0x00～0x0F ：十六进制数XX ：1个字节16进制数XXXX ：2个字节16进制数XX…XX ：未知个字节16进制数。

04
双城—拳皇
05
幽冥太—第十二 届齐鲁动漫展动 漫美少年获得者
06
摄影达人—魔导 士
A
K
感谢聆听
C
N
Aபைடு நூலகம்
K
cosplay全接触：文化新旅
演讲人 2 0 2 x - 11 - 11
C
N
目录
01. part1costar星 02. part2costar秀
01
part1costar星
part1cos tar星
ee— aliceinwo nderland
麵條—个 人合辑
华夜— ff12-弗
兰
娇娇—黑 执事-红
夫人
美歪— aion
烈— gdcrew
团长
part1cos tar星
水果稀— 我是小甜
甜
轩辕玖— 天元突破
-妮娅
蘑菇ah— 个人合辑
miluku— vocaloid
美美—个 人合辑
音迪—巡 音
part1costar星
天命紫聖—个人合辑 小嗳—人型电脑天使心 zs清浅—个人合辑 九音—原创军服 紫悠—原创lolita 小嗳—人型电脑天使心 ZS清浅—个人合辑 九音—原创军服 紫悠—原创LOLITA
02
part2costar秀
06 烈&风间召 唤—侍魂
01 墨央组—凡
尔赛玫瑰
05 蔬果村—哈
利 ·波 特
02 304—薄樱
鬼
04 304之星
03 304—完美 小姐进化论
part2costar 秀
part2costar 秀
01
米菲琳—永恒之 塔
02
湿叔—黑执事塞 巴斯

三角函数三角函数（Trigonometric）是数学中属于初等函数中的超越函数的一类函数。

它们的本质是任意角的集合与一个比值的集合的变量之间的映射。

通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。

另一种定义是在直角三角形中，但并不完全。

现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

它包含六种基本函数：正弦、余弦、正切、余切、正割、余割。

由于三角函数的周期性，它并不具有单值函数意义上的反函数。

三角函数在复数中有较为重要的应用。

在物理学中，三角函数也是常用的工具。

目录[隐藏] 定义基本公式相关计算相关概念高等数学内容定义基本公式相关计算相关概念高等数学内容定义它有六种基本函数(初等基本表示)：三角函数数值表（斜边为r，对边为y，邻边为x。

）在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设O P=r，P点的坐标为（x，y）有正弦函数sinθ=y/r 正弦（sin）:角α的对边比上斜边余弦函数cosθ=x/r 余弦（cos）:角α的邻边比上斜边正切函数tanθ=y/x 正切（tan）:角α的对边比上邻边余切函数cotθ=x/y 余切（cot）:角α的邻边比上对边正割函数secθ=r/x 正割（sec）:角α的斜边比上邻边余割函数cscθ=r/y 余割（csc）:角α的斜边比上对边以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ =1-cosθ余矢函数coversθ =1-sinθ基本公式同角三角函数关系式·平方关系：三角函数sin^2(α)+cos^2(α)=1cos^2(a)=(1+cos2a)/2tan^2(α)+1=sec^2(α)sin^2(a)=(1-cos2a)/2cot^2(α)+1=csc^2(α)·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1·商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·对称性180度-α的终边和α的终边关于y轴对称。

小小白（Cosplay角色扮演者）编辑 小小白，中国知名coser，2006年开始接触COS，出版作品有《福》、《洛幕》、《白》、《白社会》、《潋心》等。 后加入杭州玄机科技信息技术有限公司，负责2DQ版动画《秦时明月之笑闯江湖》第二季、3D动画《秦时明月之万里长城》、3D动画《秦时明月之天行九歌》、3D动画电影《秦时明月3D电影龙腾万里》、3D动画《英雄冯子材》、3D动画《秦时明月之君临天下》的宣传企划，3D动画《秦时明月之万里长城》的媒体推广、网站策划。 中文名郭许炜 外文名Guo Xuwei 别 名小小白 国 籍中国 民 族汉族 星 座巨蟹座 出生地浙江嘉兴 出生日期1986年7月5日 职 业《秦时明月》系列宣传企划 经纪公司杭州玄机科技信息技术有限公司 代表作品仙侠奇缘之花千骨-白子画、秦时明月-白凤凰、银魂—坂田银时、盗墓笔记——解语花 现居地上海 昵 称白胖子，白少，白殿，大白，白白 目录 1人物生活 ▪ 详细资料 ▪ 个人简介 ▪ 粉丝印象 2主要作品 ▪ 静态作品 ▪ 动态作品 ▪ 出版物参与 3媒体报道 4官方形象 5后援会 6活动出席 1人物生活 编辑 详细资料 性格：含蓄 内向 寡言（在微博上是个逗比） 喜欢的颜色：粉色 喜欢吃的菜：都喜欢呀 最拿手的菜：方便面 最常说的话：1、放着我来做…… 2、放着，我会吃完的…… 3、大家饿了么？…… 4、这个角色我也要出的…… 最常做的动作：低头猛吃…… 个人简介 《咎狗之血》—— 小小白 小小白，杭州玄机科技信息技术有限公司媒介部经理，国内知名Coser。由于从小喜爱动漫，2006年考入浙江科技学院学习动画设计及相关动漫产业知识学习，同年开始Cosplay生涯。长期的业内Cos活动以及众多动漫节的经历，让他在动漫产业的宣发方面积累了很多经验，曾与腾讯、网易、九城等大型门户型网站合作；受邀参加过中国国际动漫节、东京电玩节、台北书展

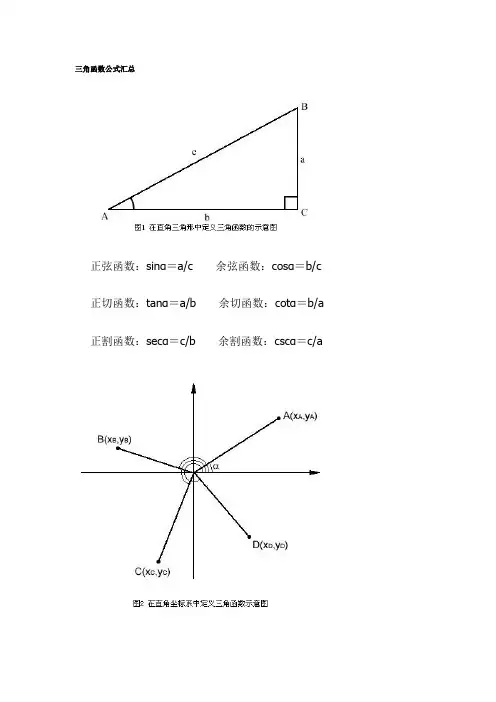
三角函数公式汇总正弦函数：sinα＝a/c余弦函数：cosα＝b/c 正切函数：tanα＝a/b余切函数：cotα＝b/a 正割函数：secα＝c/b余割函数：cscα＝c/a正弦函数：sinα＝y/r余弦函数：cosα＝x/r正切函数：tanα＝y/x余切函数：cotα＝x/y 正割函数：secα＝r/x余割函数：cscα＝r/y sin0°=0sin90°=1sin180°=0cos0°=1cos90°=0cos180°=－1tan0°=0tan90°=不存在tan180°=0 cot0°=不存在cot90°=0cot180°=不存在转化关系1、倒数关系sinα×cscα＝1cosα×secα＝1tanα×cotα＝12、平方关系1＋tan2α＝sec2α1＋cot2α＝csc2αsin2α＋cos2α＝1和角、倍角、半角公式1、和角公式sin(α＋β)＝sinαcosβ＋cosαsinβcos(α＋β)＝cosαcosβ－sinαsinβtan(α＋β)＝(tanα＋tanβ)/(1－tanαtanβ)cot(α＋β)＝(cotαcotβ－1)/(cotα＋cotβ)2、倍角公式sin2α＝2sinαcosαsin3α＝3sinα－4sin3αcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2αcos3α＝4cos3α－3cosαtan2α＝(2tanα)/1－tan2αtan(3α)=(3tanα-tan3α)/(1-3tan2α)3、半角公式sin(α/2)＝±[(1－cosα)/2]1/2cos(α/2)＝±[(1＋cosα)/2]1/2tan(α/2)＝±[(1－cosα)/(1＋cosα)]1/2＝sinα/(1＋cosα)＝(1－cosα)/ sinα4、万能公式sinα＝[2tan(α/2)]/[1＋tan2(α/2)]cosα＝[1－tan2(α/2)]/[1＋tan2(α/2)]tanα＝[2tan(α/2)]/[1－tan2(α/2)]积化和差、和差化积公式1、积化和差公式sinαsinβ＝－[cos(α＋β)－cos(α－β)]/2sinαcosβ＝[sin(α＋β)＋sin(α－β)]/2cosαsinβ＝[sin(α＋β)－sin(α－β)]/2cosαcosβ＝[cos(α＋β)＋cos(α－β)]/22、和差化积公式sinα＋sinβ＝2sin[(α＋β)/2]cos[(α－β)/2]sinα－sinβ＝2cos[(α＋β)/2]sin[(α－β)/2]cosα＋cosβ＝2cos[(α＋β)/2]cos[(α－β)/2]cosα－cosβ＝－2sin[(α＋β)/2]sin[(α－β)/2]3、辅助角公式asinα+bcosα=(a2+b2)1/2sin(а+θ)（其中：cosθ=a/[(a2+b2)1/2 ]，sinθ=b/[(a2+b2)1/2] ，tanθ=b/a ）目录 ·诱导公式·诱导公式记忆口诀·同角三角函数基本关系·同角三角函数关系六角形记忆法·两角和差公式·倍角公式·半角公式·万能公式·万能公式推导·三倍角公式·三倍角公式推导·三倍角公式联想记忆·和差化积公式·积化和差公式·和差化积公式推导诱导公式★诱导公式★常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)诱导公式记忆口诀※规律总结※上面这些诱导公式可以概括为：对于k·π/2±α(k∈Z)的个三角函数值，①当k是偶数时，得到α的同名函数值，即函数名不改变；②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan.（奇变偶不变）然后在前面加上把α看成锐角时原函数值的符号。

三宇数码科技（上海）有限公司于2003年成立，是一家专业生产各种卡片（会员卡、电信卡、刮刮卡、磁条卡、智能IC卡、可视卡），RFID技术开发及软件系统应用、推广和智能卡相关服务的日资企业，是日本理光授权的可以提供可视卡解决方案的少数几家国内公司之一，也是日本CSK软件公司的中国唯一代理商。

公司占地面积达3500平方米，员工100多人。

公司引进具有国际先进水平的制卡生产流水线，已获得了《集成电路卡注册证书》，并且通过了ISO9001:2008质量体系认证，从而提高了企业的产品质量和管理水平。

优秀的设计人才，科学先进的管理模式、完美的产品售后服务为公司的不断发展打下了坚实的基础。

公司的产品广泛应用于金融、电信、移动、社保、医疗、交通、驾驶员管理、旅游、商场、工商税务、安全控制等领域，受到各界的好评。

IC卡及COS简介IC卡（Integrated Circuit Card）也就是集成电路卡，是由法国人在70年代发明的。

国际标准组织（ISO）对IC卡的简单定义如下：一张镶嵌集成电路芯片的信用卡大小的塑胶卡片，并对于IC卡的物理和电器指标以及应用标准做出较详尽的规定～ISO7816。

IC卡的应用随着集成电路技术的飞速发展以及人们对于卡片的作用的认识逐渐成为关注的焦点。

自八十年代末，IC卡首先在欧洲大量使用，作为解决电信以及银行支付中存在的诸多问题的有效解决方案。

随后IC卡的作用被大多数人充分认识，在世界各地IC卡的应用成为了一种产业。

IC卡的应用领域也被大大扩展，目前IC卡主要应用在：（1）电信：作为GSM网络的用户识别卡～SIM卡，还作为公用电话收费卡～公用电话IC卡。

（2）银行：IC卡在银行支付行业的应用成为一种时尚，解决了磁条信用卡（银行卡）应用过程中存在的诸多问题。

有信用卡、扣帐卡、储值卡、电子钱包等多种应用。

（3）保险：IC卡作为管理社会保险以及商业保险的有效手段。

（4）付费电视：IC卡在付费电视方面的应用成为一种新的趋势。

cos
1 , 2 2 1 f x f y
cos
fy 1
O x
,

Dx y
y C
f x2 f y2
cos fy cos
定理1 目录 上页 下页 返回 结束
因此

P P cos cos d S P d x y z cos P P cos cos d S z y P P dzdx d xd y z y
(0, 0, ), r ( x, y, z )
点 M 的线速度为
l
M
i j k v r 0 0 x y z
rot v
x
( y, x, 0)
O x
r
y
i
y x 0
y
j
z
k
(0, 0, 2 ) 2
(此即“旋度”一词的来源)
通过作辅助线把 分成与z 轴只交于一点的几部分, 在每一部分上应用斯托克斯公式, 然后相加, 由于沿辅助
曲线方向相反的两个曲线积分相加刚好抵消, 所以对这
类曲面斯托克斯公式仍成立. 证毕 注意: 如果 是 xOy 面上的一块平面区域, 则斯托克斯 公式就是格林公式, 故格林公式是斯托克斯公式的特例.
同理
2
Q R P yR (3) 在G内存在某一函数 R使 d u P d x Q d证毕 d z u, z y (4) 在G内处处有P y ,
Q x Q , x z

zR ,
y
R x
P z
定理2
目录Βιβλιοθήκη 上页下页返回结束
例3. 验证曲线积分 ( y z ) d x ( z x) d y ( x y ) d z 与路径无关, 并求函数

三角函数大全三角函数是数学中属于初等函数中的超越函数的一类函数。

它们的本质是任何角的集合与一个比值的集合的变量之间的映射。

通常的三角函数是在平面直角坐标系中定义的。

其定义城为整个实数域。

另一种定义是在直角三角形中，但并不完全。

现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

目录公式分类三角关系一个特殊公式坡度公式锐角三角函数一般公式二倍角公式三倍角公式三倍角公式半角公式万能公式其他四倍角公式五倍角公式六倍角公式八倍角公式九倍角公式十倍角公式N倍角公式半角公式两角和公式三角和公式和差化积积化和差双曲函数诱导公式万能公式其它公式内容规律一些重要的定理正弦定理余弦定理展开公式分类三角关系一个特殊公式锐角三角函数一般公式二倍角公式三倍角公式三倍角公式半角公式万能公式其他四倍角公式五倍角公式六倍角公式七倍角公式八倍角公式九倍角公式十倍角公式N倍角公式半角公式两角和公式三角和公式和差化积积化和差双曲函数诱导公式万能公式其它公式内容规律一些重要的定理正弦定理余弦定理展开编辑本段公式分类三角关系倒数关系：tanα ·cotα=1sinα ·cscα=1cosα·secα=1商的关系：sinα/cosα=tanα=secα/cscα平方关系：一个特殊公式（sina+sinθ）*（sina-sinθ）=sin（a+θ）*sin（a-θ）证明：（sina+sinθ）*（sina-sinθ）=2 sin[（θ+a)/2] cos[(a-θ)/2] *2 cos[（θ+a)/2] sin[(a-θ）/2]=sin（a+θ）*sin（a-θ）[1]坡度公式我们通常把坡面的铅直高度h与水平宽度l的比叫做坡度（也叫坡比），用字母i表示，即i=h / l,坡度的一般形式写成l : m形式，如i=1:5.如果把坡面与水平面的夹角记作a（叫做坡角），那么i=h/l=tan a.锐角三角函数正弦：sinα=∠α的对边/∠α 的斜边余弦：cosα=∠α的邻边/∠α的斜边正切：tanα=∠α的对边/∠α的邻边余切：cotα=∠α的邻边/∠α的对边一般公式sin30°=二分之一sin45°=二分之根号二sin60°=二分之根号三cos30°=二分之根号三cos45°=二分之根号二cos60°=二分之一tan30°=三分之根号三tan45°=1tan60°=根号三[2]二倍角公式正弦sin2A=2sinA·cosA余弦正切tan2A=（2tanA）/（1-tan^2(A））三倍角公式三倍角公式sin3α=4sinα·sin（π/3+α）sin（π/3-α）cos3α=4cosα·cos（π/3+α）cos（π/3-α）tan3a = tan a · tan（π/3+a）· tan（π/3-a) 三倍角公式推导sin（3a)=sin(a+2a)=sin2acosa+cos2asina=2sina（1-sin^2a)+（1-2sin^2a)sina=3sina-4sin^3acos3a=cos（2a+a)=cos2acosa-sin2asina=（2cos^2a-1）cosa-2（1-cos^2a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina（3/4-sin^2a)=4sina[（√3/2）-sina][（√3/2）+sina]=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[（60+a)/2]cos[（60°-a)/2]*2sin[（60°-a)/2]cos[（60°+a)/2] =4sinasin（60°+a)sin（60°-a)cos3a=4cos^3a-3cosa=4cosa(cos^2a-3/4）=4cosa[cos^2a-（√3/2）^2]=4cosa(cosa-cos30°）(cosa+cos30°）=4cosa*2cos[(a+30°）/2]cos[(a-30°）/2]*{-2sin[(a+30°）/2]sin[(a-30°）/2]}=-4cosasin(a+30°）sin(a-30°）=-4cosasin[90°-（60°-a)]sin[-90°+（60°+a)]=-4cosacos（60°-a)[-cos（60°+a)]=4cosacos（60°-a)cos（60°+a)上述两式相比可得tan3a=tanatan（60°-a)tan（60°+a)现列出公式如下：sin2α=2sinαcosα tan2α=2tanα/（1-tan^2（α））cos2α=cos^2（α）-sin^2（α）=2cos^2（α）-1=1-2sin^2（α）可别轻视这些字符，它们在数学学习中会起到重要作用，包括在一些图像问题和函数问题中三倍角公式sin3α=3sinα-4sin^3 α=4sinα·sin（π/3+α）sin（π/3-α）cos3α=4cos^3 α-3cosα=4cosα·cos（π/3+α）cos（π/3-α）tan3α=tan（α）*(-3+tan（α）^2）/(-1+3*tan（α）^2）=tan a ·tan （π/3+a）· tan（π/3-a)半角公式sin^2（α/2）=（1-cosα）/2cos^2（α/2）=（1+cosα）/2tan^2（α/2）=（1-cosα）/（1+cosα）tan（α/2）=sinα/（1+cosα）=（1-c osα）/sinα万能公式sinα=2tan（α/2）/[1+tan^2（α/2）]cosα=[1-tan^2（α/2）]/[1+tan^2（α/2）]tanα=2tan（α/2）/[1-tan^2（α/2）]其他sinα+sin（α+2π/n)+sin（α+2π*2/n)+sin （α+2π*3/n)+……+sin[α+2π*(n-1）/n]=0cosα+cos（α+2π/n)+cos（α+2π*2/n)+cos （α+2π*3/n)+……+cos[α+2π*(n-1）/n]=0 以及sin^2（α）+sin^2（α-2π/3）+sin^2（α+2π/3）=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式sin4A=-4*(cosA*sinA*（2*sinA^2-1））cos4A=1+(-8*cosA^2+8*cosA^4）tan4A=（4*tanA-4*tanA^3）/（1-6*tanA^2+tanA^4）五倍角公式sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*（5-10*tanA^2+tanA^4）/（1-10*tanA^2+5*tanA^4）六倍角公式sin6A=2*(cosA*sinA*（2*sinA+1）*（2*sinA-1）*(-3+4*sinA^2））cos6A=((-1+2*cosA)*（16*cosA^4-16*cosA^2+1））tan6A=(-6*tanA+20*tanA^3-6*tanA^5）/(-1+15*tanA-15*tanA^4+tanA^6）七倍角公式sin7A=-(sinA*（56*sinA^2-112*sinA^4-7+64*sinA^6））cos7A=(cosA*（56*cosA^2-112*cosA^4+64*cosA^6-7））tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6）/(-1+21*tanA^2-35*tanA^4+7*tanA^6）八倍角公式sin8A=-8*(cosA*sinA*（2*sinA^2-1）*(-8*sinA^2+8*sinA^4+1））cos8A=1+（160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2）tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6）/（1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8）九倍角公式sin9A=(sinA*(-3+4*sinA^2）*（64*sinA^6-96*sinA^4+36*sinA^2-3））cos9A=(cosA*(-3+4*cosA^2）*（64*cosA^6-96*cosA^4+36*cosA^2-3））tan9A=tanA*（9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8）/（1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8）十倍角公式sin10A = 2*(cosA*sinA*（4*sinA^2+2*sinA-1）*（4*sinA^2-2*sinA-1）*(-20*sinA^2+5+16*sinA^4））cos10A = ((-1+2*cosA^2）*（256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1））tan10A = -2*tanA*（5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8）/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10）N倍角公式根据棣美弗定理，（cosθ+ i sinθ）^n = cos(nθ）+ i sin(nθ）为方便描述，令sinθ=s，cosθ=c考虑n为正整数的情形：cos(nθ）+ i sin(nθ）= (c+ i s)^n = C(n,0)*c^n + C(n,2）*c^(n-2）*(i s)^2 + C(n,4）*c^(n- 4）*(i s)^4 + ... …+C(n,1）*c^(n-1）*(i s)^1 + C(n,3）*c^(n-3）*(i s)^3 + C(n,5）*c^(n-5）*(i s)^5 + ... …=>；比较两边的实部与虚部实部：cos(nθ）=C(n,0)*c^n + C(n,2）*c^(n-2）*(i s)^2 + C(n,4）*c^(n-4）*(i s)^4 + ... …i*虚部：i*sin(nθ）=C(n,1）*c^(n-1）*(i s)^1 + C(n,3）*c^(n-3）*(i s)^3 + C(n,5）*c^(n-5）*(i s)^5 + ... …对所有的自然数n：⒈cos(nθ）：公式中出现的s都是偶次方，而s^2=1-c^2（平方关系），因此全部都可以改成以c（也就是cosθ）表示。

2
y=sin2x图象由y=sinx图象（纵标不变）， 1 横标缩短 而得。 2
y=si nx
y=si n2x
2π O x
横标伸长2倍而得。
1 y=sin 2 x图象由y=sinx图象（纵标不变），
返回目录
π 例2：如何由y=sinx 的图象得到y=3sin(2x+ 3
)
方法1：y=sinx
纵向伸长3倍

返回目录
2.求函数 y=sin4x+2 3 sinxcosx-cos4x 的最小正周期和最小值, 并写出该函数在 [0, ] 上的单调增区间. 解: ∵ y=sin4x+2 3 sinxcosx-cos4x =(sin2x-cos2x)(sin2x+cos2x)+ 3 sin2x = 3 sin2x-cos2x
2 2

(

2
k ,

2
k )( k z )
递增
递减
x 2k

2
y , k z 时， m ax 1
y , k z 时，m in 1
x 2 k , k z 时，y m a x 1
最值
奇偶性
x 2k

2
x 2k , k z
纵向伸长3倍
y=3sinx
y
方法2： y=sinx － O 6 纵向伸长3倍 y=3sinx 1 横向缩短 2 y=3sin2x π 左移 6 y=3sin(2x+π ) 3
π 3 π y=3sin(x+ 3 ) 1 横向缩短 2 π y=3sin(2x+ ) 3
左移
y=3sinx

(
z)
证明: 因为z0为f(z)的一级极点, 所以
f (z) c1(z z0 )1 c0 c1(z z0 ) K
(z z0 ) f (z) c1 c0 (z z0 ) c1(z z0 )2 K
Res[
f
(z),
z0 ]
c1
lim(z
zz0
z0 )
f
(z)
目录 上页 下页 返回 结束
即:展开式中不含(z-z0)的负幂次项, 则称z0为可去奇点.
目录 上页 下页 返回 结束
(2). 极点: 若f(z)在z0处的洛朗级数为
f (z) cm(z z0)m cm1(z z0)m1 K c1(z z0)1 c0 c1(z z0) K , cm 0
即:展开式中只有有限个(z-z0)的负幂次项, 则称z0为f(z) 的极点. 若负幂次项的次数绝对值的最大值为 m, 则称z0为m 级极点。
解: z =±i , 1 是孤立奇点.
因为 z - 2 在 z =±i , 1处解析, 且不是零点
z =±i 是分母的 1 级零点，所以是 f (z) 的1级极点; z = 1 是分母的 3 级零点，所以是 f (z) 的 3 级极点 .
目录 上页 下页 返回 结束
(2)
f
(z)
ez 1 z2
解: z = 0是孤立奇点.
1
ze z
z
1
(
1) z
1 (1)2 2! z
K
z 1 1 (1)K 2! z
Res[
f
(z), 0]
c1
1 2
目录 上页 下页 返回 结束
3. 极点的留数
z0为f(z)的极点, 则有如下法则 (1). 法则1: z0为f(z)的一级极点, 那么

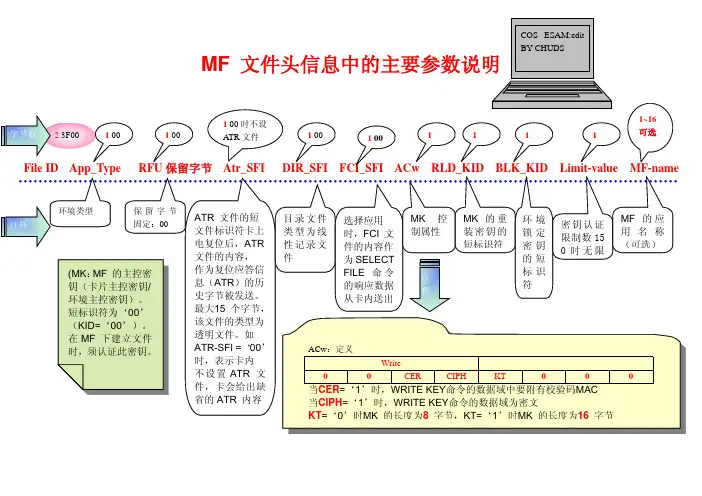
MF 文件头信息中的主要参数说明23F00字节数(MK ：MF 的主控密钥（卡片主控密钥/环境主控密钥）。

短标识符为‘00’（KID=‘00’）。

在MF 下建立文件时，须认证此密钥。

注释注释DDF文件21~16(可选可放到最后)210020*********File_ID DDF_Name LNG App_t RFU DIR_SFI FCI_SFI ACw RLD_KID BLK_KID Lim字节(MK ：DDF 的主控密钥（环境主控密钥）。

短标识符为‘00’（KID=‘00’）。

在DDF 下建立文件时，须认证此密钥ACw ：定义WriteCERCIPHKTKP1KACT当CER =‘1’时，WRITE KEY 命令的数据域中要附有校验码MAC 当CIPH =‘1’时，WRITE KEY 命令的数据域为密文KT =‘0’时MK 的长度为8字节，KT=‘1’时MK 的长度为16字节KP1，标识RLD-KID 所指密钥的位置，KP1=‘0’时，RLD-KID 所指密钥在当前DDF 下=‘1’时，RLD-KID 所指密钥在父目录下.KACT =‘0’表示不存在MK 。

可通过父目录下的主控密钥按ACw 定义的方式建立MK 。

当卡复位后，在该应用环境下不可建立任何形式的应用和文件。

KACT=‘1’表示MK 已经存在。

缺省值为全‘0’密钥长度由KT 设定注释ADF文件ADF 下密钥钥ACw ：定义WriteCERCIPHKTKP1KP2KACT当CER =‘1’时，WRITE KEY 命令的数据域中要附有校验码MAC 当CIPH =‘1’时，WRITE KEY 命令的数据域为密文KT =‘0’时MK 的长度为8字节，KT=‘1’时MK 的长度为16字节KP1，标识RLD-KID 所指密钥的位置，KP1=‘0’时，RLD-KID 所指密钥在当前ADF 下,=‘1’时，RLD-KID 所指密钥在父目录下.KACT =‘0’表示不存在MK 。

SmartCOS ®IC卡及COS简介IC卡（Integrated Circuit Card）也就是集成电路卡，是由法国人在70年代发明的。

国际标准组织（ISO）对IC卡的简单定义如下：一张镶嵌集成电路芯片的信用卡大小的塑胶卡片，并对于IC卡的物理和电器指标以及应用标准做出较详尽的规定～ISO7816。

IC卡的应用随着集成电路技术的飞速发展以及人们对于卡片的作用的认识逐渐成为关注的焦点。

自八十年代末，IC卡首先在欧洲大量使用，作为解决电信以及银行支付中存在的诸多问题的有效解决方案。

随后IC卡的作用被大多数人充分认识，在世界各地IC卡的应用成为了一种产业。

IC卡的应用领域也被大大扩展，目前IC卡主要应用在：（1）电信：作为GSM网络的用户识别卡～SIM卡，还作为公用电话收费卡～公用电话IC卡。

（2）银行：IC卡在银行支付行业的应用成为一种时尚，解决了磁条信用卡（银行卡）应用过程中存在的诸多问题。

有信用卡、扣帐卡、储值卡、电子钱包等多种应用。

（3）保险：IC卡作为管理社会保险以及商业保险的有效手段。

（4）付费电视：IC卡在付费电视方面的应用成为一种新的趋势。

（5）身份识别：有些国家已经开展了IC卡在出入境管理等方面的应用。

（6）门径控制：IC卡作为关键部门进出入管理方面的有效媒介。

（7）管理服务：利用IC卡的诸多特点，应用IC卡于政府部门的管理工作。

国内类似的应用有税务申报IC卡、工商企业管理卡等。

IC卡根据集成电路芯片的特性分为智能卡和存储卡。

智能卡的集成电路芯片是一个MCU（微控制单元）。

在单元里有ROM（用于存储指令代码）、RAM、EEPROM（作为用户数据存储）和CPU。

很多人又【1】深圳市明华奥汉磁卡系列有限公司北京市明华奥汉科技有限公司SmartCOS ®把智能卡称为CPU卡。

有关智能卡与外界交换信息的电气指标以及指令格式在ISO7816-3&4中有详细的规定。

三角函数值特殊角三角函数值三角函数是数学中属于初等函数中的超越函数的一类函数。

它们的本质是任意角的集合与一个比值的集合的变量之间的映射。

通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。

另一种定义是在直角三角形中，但并不完全。

现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

由于三角函数的周期性，它并不具有单值函数意义上的反函数。

目录编辑本段应用三角函数在复数中有较为重要的应用。

在物理学中，三角函数也是常用的工具。

它有六种基本函数：函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数 sin（A）=a/c余弦函数 cos（A）=b/c正切函数 tan（A）=a/b余切函数 cot（A）=b/a其中a为对边，b为邻边，c为斜边编辑本段三角函数值表sin0=0cos0=1tan0=0sin15=（√6-√2）/4cos15=（√6+√2）/4tan15=sin15/cos15=2-√3sin30=1/2cos30=√3/2tan30=√3/3sin45=√2/2cos45=sin45=√2/2tan45=1sin60=√3/2cos60=1/2tan60=√3sin75=cos15cos75=sin15tan75=sin75/cos75 ＝2＋√3sin90=cos0cos90=sin0tan90无意义sin105=cos15cos105=-sin15tan105=-cot15sin120=cos30cos120=-sin30tan120=-tan60sin135=sin45cos135=-cos45tan135=-tan45sin150=sin30cos150=-cos30tan150=-tan30sin165=sin15cos165=-cos15tan165=-tan15sin180=sin0cos180=-cos0tan180=tan0sin195=-sin15cos195=-cos15tan195=tan15sin360=sin0cos360=cos0tan360=tan0cos72=[(√5)-1]/4（利用黄金等腰三角形可得出）sin1=0.01745240643728351 sin2=0.03489949670250097 sin3=0.05233595624294383sin4=0.0697564737441253 sin5=0.08715574274765816sin6=0.10452846326765346sin7=0.12186934340514747 sin8=0.13917310096006544 sin9=0.15643446504023087sin10=0.17364817766693033 sin11=0.1908089953765448 sin12=0.20791169081775931sin13=0.22495105434386497 sin14=0.24192189559966773 sin15=0.25881904510252074sin16=0.27563735581699916 sin17=0.2923717047227367 sin18=0.3090169943749474sin19=0.3255681544571567 sin20=0.3420201433256687 sin21=0.35836794954530027sin22=0.374606593415912 sin23=0.3907311284892737sin24=0.40673664307580015sin25=0.42261826174069944 sin26=0.4383711467890774 sin27=0.45399049973954675sin28=0.4694715627858908 sin29=0.48480962024633706 sin30=0.49999999999999994sin31=0.5150380749100542 sin32=0.5299192642332049 sin33=0.544639035015027sin34=0.5591929034707468 sin35=0.573576436351046 sin36=0.5877852522924731sin37=0.6018150231520483 sin38=0.6156614753256583 sin39=0.6293203910498375sin40=0.6427876096865392 sin41=0.6560590289905073 sin42=0.6691306063588582sin43=0.6819983600624985 sin44=0.6946583704589972 sin45=0.7071067811865475sin46=0.7193398003386511 sin47=0.7313537016191705 sin48=0.7431448254773941sin49=0.7547095802227719 sin50=0.766044443118978 sin51=0.7771459614569708sin52=0.7880107536067219 sin53=0.7986355100472928 sin54=0.8090169943749474sin55=0.8191520442889918 sin56=0.8290375725550417 sin57=0.8386705679454239sin58=0.848048096156426 sin59=0.8571673007021122 sin60=0.8660254037844386sin61=0.8746197071393957 sin62=0.8829475928589269 sin63=0.8910065241883678sin64=0.898794046299167 sin65=0.9063077870366499 sin66=0.9135454576426009sin67=0.9205048534524404 sin68=0.9271838545667873 sin69=0.9335804264972017sin70=0.9396926207859083 sin71=0.9455185755993167 sin72=0.9510565162951535sin73=0.9563047559630354 sin74=0.9612616959383189 sin75=0.9659258262890683sin76=0.9702957262759965 sin77=0.9743700647852352 sin78=0.9781476007338057sin79=0.981627183447664 sin80=0.984807753012208 sin81=0.9876883405951378sin82=0.9902680687415704 sin83=0.992546151641322 sin84=0.9945218953682733sin85=0.9961946980917455 sin86=0.9975640502598242 sin87=0.9986295347545738sin88=0.9993908270190958 sin89=0.9998476951563913 sin90=1cos1=0.9998476951563913 cos2=0.9993908270190958 cos3=0.9986295347545738cos4=0.9975640502598242 cos5=0.9961946980917455 cos6=0.9945218953682733cos7=0.992546151641322 cos8=0.9902680687415704 cos9=0.9876883405951378cos10=0.984807753012208 cos11=0.981627183447664 cos12=0.9781476007338057cos13=0.9743700647852352 cos14=0.9702957262759965 cos15=0.9659258262890683cos16=0.9612616959383189 cos17=0.9563047559630355 cos18=0.9510565162951535cos19=0.9455185755993168 cos20=0.9396926207859084 cos21=0.9335804264972017cos22=0.9271838545667874 cos23=0.9205048534524404 cos24=0.9135454576426009cos25=0.9063077870366499 cos26=0.898794046299167 cos27=0.8910065241883679cos28=0.882947592858927 cos29=0.8746197071393957 cos30=0.8660254037844387cos31=0.8571673007021123 cos32=0.848048096156426 cos33=0.838670567945424cos34=0.8290375725550417 cos35=0.8191520442889918 cos36=0.8090169943749474cos37=0.7986355100472928 cos38=0.7880107536067219 cos39=0.7771459614569709cos40=0.766044443118978 cos41=0.754709580222772 cos42=0.7431448254773942cos43=0.7313537016191705 cos44=0.7193398003386512 cos45=0.7071067811865476cos46=0.6946583704589974 cos47=0.6819983600624985 cos48=0.6691306063588582cos49=0.6560590289905074 cos50=0.6427876096865394 cos51=0.6293203910498375cos52=0.6156614753256583 cos53=0.6018150231520484 cos54=0.5877852522924731cos55=0.5735764363510462 cos56=0.5591929034707468 cos57=0.5446390350150272cos58=0.5299192642332049 cos59=0.5150380749100544 cos60=0.5000000000000001cos61=0.4848096202463371 cos62=0.46947156278589086 cos63=0.4539904997395468cos64=0.43837114678907746 cos65=0.42261826174069944 cos66=0.4067366430758004cos67=0.3907311284892737 cos68=0.3746065934159122 cos69=0.35836794954530015cos70=0.3420201433256688 cos71=0.32556815445715675 cos72=0.30901699437494745cos73=0.29237170472273677 cos74=0.27563735581699916 cos75=0.25881904510252074cos76=0.24192189559966767 cos77=0.22495105434386514 cos78=0.20791169081775923cos79=0.19080899537654491 cos80=0.17364817766693041 cos81=0.15643446504023092cos82=0.13917310096006546 cos83=0.12186934340514749 cos84=0.10452846326765346cos85=0.08715574274765836 cos86=0.06975647374412523 cos87=0.052335956242943966cos88=0.03489949670250108 cos89=0.0174524064372836 cos90=0tan1=0.017455064928217585 tan2=0.03492076949174773 tan3=0.052407779283041196tan4=0.06992681194351041 tan5=0.08748866352592401 tan6=0.10510423526567646tan7=0.1227845609029046 tan8=0.14054083470239145 tan9=0.15838444032453627tan10=0.17632698070846497 tan11=0.19438030913771848 tan12=0.2125565616700221tan13=0.2308681911255631 tan14=0.24932800284318068 tan15=0.2679491924311227tan16=0.2867453857588079 tan17=0.30573068145866033 tan18=0.3249196962329063tan19=0.34432761328966527 tan20=0.36397023426620234 tan21=0.3838640350354158tan22=0.4040262258351568 tan23=0.4244748162096047 tan24=0.4452286853085361tan25=0.4663076581549986 tan26=0.4877325885658614 tan27=0.5095254494944288tan28=0.5317094316614788 tan29=0.554309051452769 tan30=0.5773502691896257tan31=0.6008606190275604 tan32=0.6248693519093275 tan33=0.6494075931975104tan34=0.6745085168424265 tan35=0.7002075382097097 tan36=0.7265425280053609tan37=0.7535540501027942 tan38=0.7812856265067174 tan39=0.8097840331950072tan40=0.8390996311772799 tan41=0.8692867378162267 tan42=0.9004040442978399tan43=0.9325150861376618 tan44=0.9656887748070739 tan45=0.9999999999999999tan46=1.0355303137905693 tan47=1.0723687100246826 tan48=1.1106125148291927tan49=1.1503684072210092 tan50=1.19175359259421 tan51=1.234897156535051tan52=1.2799416321930785 tan53=1.3270448216204098 tan54=1.3763819204711733tan55=1.4281480067421144 tan56=1.4825609685127403 tan57=1.5398649638145827tan58=1.6003345290410506 tan59=1.6642794823505173 tan60=1.7320508075688767tan61=1.8040477552714235 tan62=1.8807264653463318 tan63=1.9626105055051503tan64=2.050303841579296 tan65=2.1445069205095586 tan66=2.246036773904215tan67=2.355852365823753 tan68=2.4750868534162946 tan69=2.6050890646938023tan70=2.7474774194546216 tan71=2.904210877675822 tan72=3.0776835371752526tan73=3.2708526184841404 tan74=3.4874144438409087 tan75=3.7320508075688776tan76=4.0107809335358455 tan77=4.331475874284153 tan78=4.704630109478456tan79=5.144554015970307 tan80=5.671281819617707 tan81=6.313751514675041tan82=7.115369722384207 tan83=8.144346427974593 tan84=9.514364454222587tan85=11.43005230276132 tan86=14.300666256711942 tan87=19.08113668772816tan88=28.636253282915515 tan89=57.289961630759144 tan90=无取值编辑本段数学方程式数关系tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1商数关系tanα=sinα/cosα cotα=cosα/sinα平方关系sinα²+cosα²=11+tanα²=secα²1+cotα&sup2=cscα²以下关系，函数名不变，图像看象限.sin（2kπ＋α）＝sinαcos（2kπ+α）=cosαtan（2kπ+α）=tanαcot（2kπ+α）=cotαsin（π＋α）=-sinαcos（π＋α）=-cosαtan（π＋α）=tanαcot（π＋α）=cotαsin（π－α）=sinαcos（π－α）=-cosαtan（π－α）=-tanαcot（π－α）=-cotαsin（2π－α）＝-sinαcos（2π－α）＝cosαtan（2π－α）＝-tanαcot（2π－α）＝-cotα以下关系，奇变偶不变，符号看象限sin（90°-α）=cosαcos（90°-α）=sinαtan（90°-α）=cotαcot（90°-α）=tanαsin（90°+α）=cosαcos（90°+α）=-sinαtan（90°+α）=-cotαcot（90°+α）=-tanαsin（270°-α)=-cosαcos（270°-α)=-sinαtan（270°-α)=cotαcot（270°-α)=tanαsin（270°+α）=－cosαcos（270°+α）=sinαtan（270°+α）=-cotαcot（270°+α）=-tanα积化合差公式sinα ·cosβ=（1/2）*[sin（α＋β）＋sin（α－β）] cosα ·sinβ=（1/2）*[sin（α＋β）－sin（α－β）] cosα ·cosβ=（1/2）*[cos（α＋β）＋cos（α－β）] sinα ·sinβ=（1/2）*[cos（α＋β）－cos（α－β）]和差化积公式sinα+sinβ=2*[sin(α+β)/2]*[cos(α-β)/2]sinα-sinβ=2*[cos(α+β)/2]*[sin(α-β)/2]cosα+cosβ=2*[cos(α+β)/2]*[cos(α-β)/2]cosα-cosβ=-22*[sin(α+β)/2]*[sin(α-β)/2]三倍角公式sin3α=3sinα-4sinα³cos3α=4cosα³-3cosα两角和与差的三角函数关系sin（α+β）=sinαcosβ+cosαsinβsin（α-β）=sinαcosβ-cosαsinβcos（α+β）=cosαcosβ-sinαsinβcos（α-β）=cosαcosβ+sinαsinβtan（α+β）=(tanα+tanβ )/(1－tanα ·tanβ)tan（α－β）=(tanα-tanβ )/(1+tanα ·tanβ)正弦二倍角公式：sin2α = 2cosαsinα推导：sin2A=sin(A+A)=sinAcosA+cosAsinA=2sinAcosA拓展公式：sin2A=2sinAcosA=2tanAcos^2A=2tanA/[1+tan^2A] 1+sin2A=(sinA+cosA)^2余弦二倍角公式：余弦二倍角公式有三组表示形式，三组形式等价：1.Cos2a=Cos^2a-Sin^2a=[1-tan^2a]/[1+tan^2a]2.Cos2a=1-2Sin^2a3.Cos2a=2Cos^2a-1推导：cos2A=cos(A+A)=cosAcosA-sinAsinA=cos^2A-sin^2A=2cos^2A-1 =1-2sin^2A正切二倍角公式：tan2α=2tanα/[1-tan^2α]推导：tan2A=tan(A+A)=(tanA+tanA)/(1-tanAtanA)=2tanA/[1-tan^2A]降幂公式：cosA^2=[1+cos2A]/2sinA^2=[1-cos2A]/2tanA^2=[1-cos2A]/[1+cos2A]变式：sin2α=sin^2(α+π/4)-cos^2(α+π/4)=2sin^2(a+π/。

sin(n+a) =—sin a
cos ( n + a ) = —cos a
tan ( n + a ) = tan a
cot ( n + a ) =cot a
公式三
公式三：
任意角
sin(―
cos(—
a与的三角函数值之间的关系：
-a) =— sin a
-a)=cos a
tan(—
cot(—
-a ) =—tan a
•降幕公式
•降幕公式：
sir/2(a ) = (1-cos (2a)) /2=versin (2 a )/2
cos"2 ( a ) = (1+cos (2a)) /2=vercos (2 a )/2
tan"2 ( a ) = (1-cos (2 a ))/(1+cos (2a))
・万能公式
•万能公式：
sin
(2
JI
—a
)=—sin a
cos
(2
JI
—a
)=cos a
tan
(2
JI
—a
)=—tan a
cot
(2
JI—a)=—co来自 a公式六公式六：
n/2±a及3Ji/2±a与a的三角函数值之间的关系:
sin
(n /2+a ) =cos a
cos
(n /2+a ) = — sin a
tan
(n /2+a ) = —cot a
cot
(3 Ji /2+ a ) = — tan a
sin
(3 Ji /2— a ) = —cos a
cos
(3 Ji /2— a ) = — si na

3）安全隔离与信息交换产品
安全隔离与信息交换产品是指能够保证不同网络之间在网络协议终止的基础上，通过安全通道在实现网络隔离的同时进行安全数据交换的软硬件组合。
适用的产品范围为：（1）安全隔离与信息交换产品；（2）安全隔离与文件单向传输产品。
2、通信安全
4）安全路由器
安全路由器是指为保障所传输数据完整性、机密性、可用性，应用于重要信息系统的，具备IKE密钥协商能力，端口IPSec硬件线速加密能力的路由器。
7、评估审计与监控
10）入侵检测系统（IDS）
入侵检测系统指通过对计算机网络或计算机系统中的若干关键点收集信息并对其进行分析，发现违反安全策略的行为和被攻击迹象的软件或软硬件组合。
适用的产品范围为：（1）网络型入侵检测系统；（2）主机型入侵检测系统。
11）网络脆弱性扫描产品
网络脆弱性扫描产品指利用扫描手段检测目标网络系统中可能被入侵者利用的脆弱性的软件或软硬件组合。
8、应用安全
13）网站恢复产品
网站恢复产品是对受保护的静态网页文件、动态脚本文件及目录的未授权更改及时地进行自动恢复的软件或软硬件组合。
适用的产品范围为：针对静态网页文件、动态脚本文件及目录进行自动恢复的产品。
网络安全隔离卡是指安装在计算机内部，能够使连接该计算机的多个独立的网络之间仍然保持物理隔离的设备。安全隔离线路选择器是与配套的安全隔离卡一起使用，适用于单网布线环境下，使同一计算机能够访问多个独立的网络，并且各网络仍然保持物理隔离的设备。
适用的产品范围为：（1）安全隔离计算机；（2）安全隔离卡；（3）安全隔离线路选择器。
7）安全操作系统
安全操作系统是指从系统设计、实现、使用和管理等各个阶段都遵循一套完整的系统安全策略，并实现了GB 17859-1999《计算机信息系统等级保护划分准则》所确定的安全等级三级（含）以上的操作系统。

三角函数积分表
目录:
1. 积分只有 sin的函数
2. 积分只有 cos的函数
3. 积分只有 tan的函数
4. 积分只有 sec的函数
5. 积分只有 csc的函数
6. 积分只有 cot的函数
7. 积分只有 sin和 cos的函数
8. 积分只有 sin和 tan的函数
9. 积分只有 cos和 tan的函数
10. 积分只有 sin和 cot的函数
11. 积分只有 cos和 cot的函数
12. 积分只有 tan和 cot的函数
1. 积分只有sin的函数
其中
其中
（其中是Coversine函数）
其中
其中
其中
其中
2. 积分只有cos的函数
3. 积分只有tan的函数
4. 积分只有sec的函数
5. 积分只有csc
的函数
6. 积分只有
cot的函数
7. 积分只有sin和cos的函数
also:
also:
also:
also:
also:
8. 积分只有sin和tan的函数
9. 积分只有cos和tan的函数
10. 积分只有sin和cot的函数
11. 积分只有cos和cot的函数
12. 积分只有tan和cot的函数。