「働くこと」に结びつく学习理论と実践活动(IV教育心理学と実(精)
- 格式:pdf
- 大小:879.21 KB
- 文档页数:8

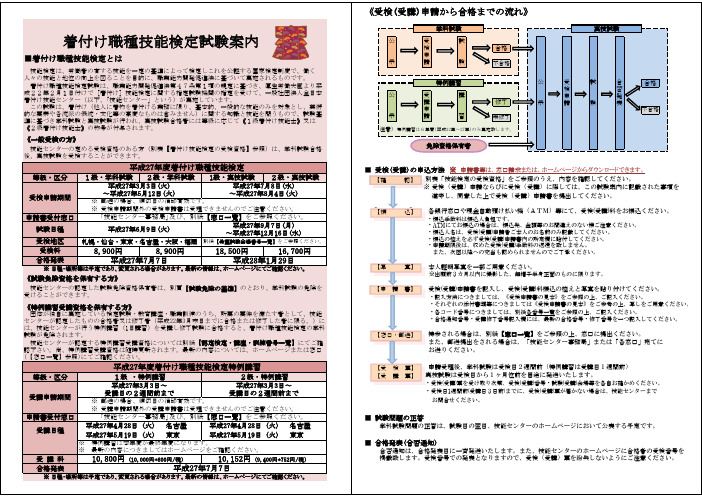
【確 認】 別表「技能検定の受検資格」をご参照のうえ、内容を確認してください。
※ 受検(受講)申請ならびに受検(受講)に際しては、この試験案内に記載された事項を【振 込】 各銀行窓口や現金自動預け払い機(ATM)等にて、受検(受講)料をお振込ください。
・振込手数料は振込人負担です。
・ATMにてお振込の場合は、振込先、金額等のお間違えのない様ご注意ください。
【写 真】 本人証明写真を一部ご用意ください。
※出願前3カ月以内に撮影した、無帽子半身正面のものに限ります。
【申 請 書】 受検(受講)申請書を記入し、受検(受講)料振込の控えと写真を貼り付けてください。
・記入方法につきましては、《受検申請書の見本》をご参照の上、ご記入ください。
・それぞれの添付書類等につきましては《受検申請書の見本》をご参考の上、写しをご用意ください。
【窓口・郵送】 持参される場合は、別紙 お送りください。
【受 検 票】 申請受理後、学科試験は受検日2週間前(特例講習は受講日1週間前) 実技試験は受検日から1ヶ月位前を目途に発送いたします。
・受検(受講)票を受け取り次第、受検(受講)番号・試験(受講)会場等を各自お確かめください。
・受検日1週間前(受講日3日前)までに、受検(受講)票が届かない場合は、技能センターまで
また、郵送提出をされる場合は、「技能センター事務局」または「各窓口」宛てに【確認】【振込】
【写真】
【申請書】
【窓口・郵送】
【受検票】
【受講票】。

206教育実習教育実習をを通じてじて見見えてきたえてきた非母語話者日本語教師非母語話者日本語教師非母語話者日本語教師のの利点利点陳 良慶要旨要旨筆者は、国際教養大学専門職大学院グローバル・コミュニケーション実践研究科日本語教育実践領域在学中に3学期に亘って教育実習を体験した。
日本語母語話者の実習生とともに実習を行い、同じ授業内容を担当したが、非日本語母語話者である筆者は文法や発音の間違いをしばしば指摘され、教えることをあきらめかけた時もあった。
しかし、海外教育実習で、母語を使って同じ母語の学習者に文法を指導した際、学習者からもらった感謝の言葉で、今まで気づかなかった非母語話者日本語教師の利点に気づいた。
因って、本稿では、非母語話者教師の利点について述べることにした。
更に、自己評価を通して、そうした利点が十分発揮できたかどうか自己点検し、非母語話者日本語教師の養成について述べる。
キーワードキーワード:非母語話者日本語教師、自己評価チェックリスト1.1. はじめにはじめに筆者の母語は閩南語及び北京語である。
台湾では高校から大学まで計7年間日本語学科に所属し、1年間日本の大学に留学した経験もある。
将来、日本語教育の職に就くことを考え、国際教養大学専門職大学院グローバル・コミュニケーション実践研究科日本語教育実践領域に入学し日本語教授法等の専門知識を獲得するための努力を続けてきた。
日本語教師を目指す母語話者実習生たち(以下、NS 実習生)と同じ条件で、媒介言語の使用を最小限にして実習授業を担当した。
本学大学院の教育実習においては、学習者のレベルに沿って教案を自ら作成し、教壇に立ち教育実習を行う。
秋実習(2011年9月~12月)と冬実習(2012年1月)は本学内で、それぞれ学内の交換留学生、台湾からの短期プログラム参加者を対象に実施された。
海外春実習(2012月3月)はマレーシアで実施された。
実習現場のビデオ撮影や大学院教員及び他の実習生による評価を参考にしながら、教え方の改善を図った。
1.はじめに わが国最初の保育者養成は1879(明治12)年に官立の東京女子師範学校に保姆練習科が設置されたことにより開始された。
しかし,これは第1回の卒業生を出しただけで廃止となり,同校本科に幼稚保育術と幼稚園実地保育という科目が組み込まれた。
その後は小学校教員養成に付随して保育者養成が行われた。
また,官立学校における保育者養成を基盤にしつつ,各幼稚園での見習い制や東京府教育会による速成養成がなされた。
キリスト教系では桜井女学校幼稚保育科1が最初の保育者養成機関であった。
これは米国長老派教会の宣教師であるエリザベス・パットン・ミリケン(Elizabeth Patton Milliken, 1860-1951)によって1884年に始められ,1898年に廃止されるまでに,少なくとも43名の卒業生を輩出し,私立における保育者養成の先駆となった。
戦前の保育者養成においては,官立に対し,キリスト教系保育者養成機関の方が優れた養成を行なってきたといわれながら2,その存在は傍流に位置づけられてきた。
それは,保育者養成の内容や養成された保育者の資質能力,また,その後の成長に対する実証的研究がほとんどないためである。
そこで,本稿では,草創期におけるキリスト教系保育者養成機関が養成した保育者の思想や実践を明らかにするため,桜井女学校幼稚保育科卒業生である吉田(春日)鉞エツに注目する。
幼稚保育科卒業生の中で,とりわけ吉田は多くのキリスト教系幼稚園に関わっており,幼稚園教育のパイオニアとして知られている。
彼女は『日本幼児保育史』において,明治時代の幼稚園設立に貢献した婦人として「春日鉞のようなクリスチャンの保姆等の努力がめだっている」3と評価されている。
また,『日本基督教幼稚園史』では「最初の基督教幼稚園保姆」として取り上げられ4,『キリスト教保育に捧げた人々』5にも紹介されている。
これらの先行研究では,彼女が多くの幼稚園を設立し,主任保姆として活躍したと指摘されてきたが,彼女の保育実践の内容や特質については具体的に検討されていない。


結び目理論の科学への応用-プリオン分子モデルとこころのモデルを中心として河内明夫(大阪市立大学大学院理学研究科)結び目理論という学問があることを, 寺阪英孝先生の1971年の幾何学の講義で初めて教わったときから, 報告者は結び目に興味を持ち研究してきた. 寺阪先生は, 実際にひもを使って結び目をつくって話をされたのであるが, その印象もあり当初から結び目理論が数学だけでは割り切れない要素を含んでいることを感じ, 結び目の数学研究ばかりでなく, いろいろな学問との関わりについても興味を持ち探求してきた. それを披露できるこのような機会を与えてくれたこと対し担当の先生方にお礼申し上げます.内容構成については, まず結び目・絡み目・空間グラフの数学とサイエンスについて, 具体例に基づいて説明を行う. それから, サイエンスへ応用する結び目の数学の例として, プリオン蛋白分子モデルの結び目理論と「こころ」のモデルの結び目理論―こころの有り様を図示する試み―について解説する.図1.1:結ばれていない(左側), ひとえ結び(中央), 8の字結び(右側)図1.2: 自明な結び目(左側)三葉結び目(中央) 8の字結び目(右側)1.結び目・絡み目・空間グラフの数学とその科学的意味を考える結び目とは, 3次元空間内に置かれた1本のひもの状態のことである(図1.1). 数学では結び目は閉じたひもとして考える(図1.2). 絡み目とは, いくつかの閉じたひもの結び目の集まりのことである(図1.3). また空間グラフとは, 3次元空間に埋め込まれたグラフで, 孤立した頂点(次数0の頂点)や1本の辺としか繋がらないような頂点(次数1の頂点)をもたないようなもののことである図1.3:ホップの絡み目(上左側), ボロミアン環(上右側), オリンピック・マーク(下)図1.4:樹下のθ曲線=図1.5(図 1.4). 数学の結び目理論とは, 結び目, 絡み目, あるいは空間グラフの, モノとしては同じだが, 配置が異なる場合のその差異を数学を使って研究する学問であるといえる.1) 両端のあるひもの結び目, 両端のあるひもを含む絡み目, あるいは次数1の頂点をもつ空間グラフを考えることもあるが, そのときにはそれらがある3次元閉領域に入っており, かつ端点のすべてがその領域の境界上にあると考えるならば, それらは結び目理論として意味を持つ(図1.5).2) このような3次元閉領域と端点をもつ結び目・絡み目あるいは次数1の頂点をもつ空間グラフの組は, タングルと呼ばれるが, 結び目理論の研究においては有用な概念である. 歴史的には結び目理論はトポロジー(位相幾何学)の分野と考えられてきたのであるが, その理由としては2つの与えられた結び目・絡み目あるいは空間グラフが同じものであるとすべき条件が連続的な1対1対応(同相写像)というトポロジーの言葉で与えられていることが大きい. ここでは, 次の定義により話をすすめる.=定義: 2つの与えられた結び目(あるいは絡み目,空間グラフ)が同じ(同型)であるとは, それらを(伸び縮みや変形可能なひもとみなして)あやとりの要領で同じ形に変形できるということである. 言いかえると, それらを(伸び縮みや変形可能なひもとみなして)有限回のライデマイスター移動(図1.6)により移りあうことである.図1.6:ライデマイスター移動図1.7:結び目表(同型なもの, 鏡像に同型なもの, 素でないものを除く)3)数学研究としての結び目理論の主要目的は, つぎのようなものである.(1) どのような結び目・絡み目があるかを研究し, それらを重複なしにリストアップすること(2) 2つの与えられた結び目・絡み目が, 同じ(同型)かどうかを判定すること“重複なしにリストアップする”とは, 例えば, 図1.7のような表を作成することである. 図1.8の左図の結び目は, 右図の結び目と同型で自明な結び目である. もしこの事実を予め知っているのでなければ, どのようにしてそれが自明な結び目であることを知ることができるだろうか?この問いに思いをめぐらすならば, 与えられた結び目が自明な結び目かどうかを判定するだけでも大変に難しい問題であることに気づくはずである. 同じ結び目ならば同じ値をとるような, 計算可能な位相不変量の開発という数学による考察が必要な理由はここにある.図1.8結び目が文化人類学とも関わる話題として, 組みひもの特別な場合である三つ編みをここで取り上げよう.例: 三つ編み(縄文土器にも見られる)図1.9は, 縄文時代の土器から拓本により写し取ったもののコピーであるが, 三つ編み部分がきれいに見てとれる.三つ編みの手法により, 短いひもから長い丈夫なひもを作ることができるが, この縄文土器から, 尐なくとも縄文時代にはその技術が知られていたことがわかる. また, この三つ編みを図1.10のようにつなぐと, 古くから贈物の飾りである「水引き」の結び目(あわび結び)ができる. このことは, 古くから日本には結び目文化があった証しのように思われる. この議論のどこが数学かといえば, 図1.10にをつけた部分のような同型を見つけたり, それを示したり(あるいは同型でないことを示したり)するのが結び目の数学である. 実際, この同型は, 図1.11のように(両端部分の領域を動かすことなく)変形して, 示すことができる.図1.9:北海道恵庭市ユカンボシE8遺跡B地点から出土(縄文時代前期)4)図1.10:「水引き」の結び目(あわび結び)図1.11:部分の同型の証明図1.12:チェーンさて, サイエンスにおける結び目とは何かについてであるが, 数学ではひもは線のことであるが, サイエンスにおいてはひもとみなせる対象がひもであるといえよう. 例えば, 図1.12のチェーンは, 絡み目と考えることもあるし, また1本のひもと考えることもある. サイエンスの理解が深まるにつれ, ひもとみなせる対象もより広がっている. 点は時間の軌跡を考えれば線になり, また線は時間の軌跡を考えれば面になるのだから, サイエンスにおける結び目の研究対象としては,・3次元空間(3次元としてみた宇宙)内の“ひも”・4次元空間(時空)内の“曲面”であるといえ, サイエンスにおける結び目の数学の役割として次の2点を挙げることができよう.(1)それぞれのサイエンスにおいて課された条件の下で, どのような絡まり方が可能かを研究し, それらを重複なしにリストアップすること(2) 2つのひも(あるいは曲面)の絡まりが与えられているときに, それらは同じか違うかを判定することサイエンスとしてのひも(結び目,絡み目,空間グラフ)の例を見てみよう.例: ヤン・バクスター方程式図1.13は, 平面上を衝突しないで動いた3つの粒子の時間変化の軌跡の間の等式, ヤン・バクスター方程式(行列の方程式として表現される)を表しているが, その解からジョーンズ方程式などの結び目, 絡み目, あるいは空間グラフに対する位相不変量が得られることが知られている.5)図1.13:ヤン・バクスター方程式例: DNA結び目DNA(デオキシリボ核酸)を1本のひもとみなすと, ヒトのDNA は両端のある長いひもである. ウイルスやバクテリアの場合には閉じたひもになる場合があり図1.14のような閉じた結び目になる.図1.14:環状DNA: 掲載に当たってN. R. Cozzarelliに感謝する(S. A. Wassermann, J. M. Dungan, N. R. Cozzarelli, Science, 229(1985), 171-174参照)例:ひも状ウイルス図1.15のエボラ出血熱のウイルスはひも状のRNA(リボ核酸)ウイルスとして知られている. エボラ出血熱は死亡率の高い病気である.図1.15:エボラ出血熱ウイルス/Japanese/disease-prevention/ infectious-diseases/virusebola/Pictures-Of-The-Effects-Of-Ebola.html参照例:分子の立体構造原子を点で表し, 原子の結合を線で表すと, 分子は分子グラフと呼ばれるような結び目・絡み目や空間グラフとみなせるようになる(図1.16参照).ホップの絡み目(図1.4)の分子H34C66O2は, 1960年に初めて合成された連結でなくかつ分離もできない分子で,カテナンとよばれている.6)これは3次元空間の中にあることで初めて意味を持つ分子である. 近年になって, 電子顕微鏡など科学技術の発展により, 結び目理論として興味のある分子が次々と合成されている. 三葉結び目(図1.3 ) の分子も合成されている.7)また, ボロミアン環(図1.4)の分子も合成されている.8) 棒状分子が環状分子に図1.17のように突き刺ささり, 両端にストッパーがあって抜けなくなったロタキサンと呼ばれる興味深い分子もある(輪の数が2個以上のときにはポリロタキサンという).9)たくさんのポリロタキサンが配置された状態で, それらの環状分子を繋ぐことにより新分子が構成される仕組みであるロタキサンネットワークやより一般の分子機械は, 結び目理論の知識の活用が期待できる合成化学の研究分野と思われる.10)分子グラフの絡まりの違いを明確に区別することの重要性として, 血液型, 薬の効き目, 蛋白質のアミノ酸配列などがよく知られている. 例えば, アミノ酸には互いに鏡像の関係にある2種類があり, その一方のものだけをペプチド結合によりつながれてできるひも状のものがタンパク分子というわけである. 数学における空間グラフのカイラリティ問題, すなわち与えられた空間グラフとその鏡像が同型でないかどうかを判定する問題は, 化学においても重要な問題である(図1.18参照).図1.16:分子グラフ図1.17:ポリロタキサン図1.18:有向ホップ絡み目が含むという理由でカイラルとなる空間グラフの例例:宇宙の大規模構造トポロジーは距離とは無関係な概念であるので, ミクロの世界とマクロの世界で類似性があってもおかしくはない. 宇宙の大規模構造についても近年知られるようになった.銀河を点として3次元宇宙の中に配置していくと興味深いものが見えてくる. 銀河の全体は, 銀河団を頂点とするような網目状の空間グラフを形成しており, さらに超銀河団はフィラメント状の壁をつくっている(図1.19参照).11)図1.19:国立天文台4次元デジタル宇宙プロジェクト提供今までに述べてきたサイエンスとしてのひもの例が指し示しているのは森羅万象の基本には結び目がある!という考えである. サイエンスにおける結び目理論とは, 基本となる数学の結び目理論の上に立って, 次の質問に答えることであろう.質問:3次元宇宙内のひもとみなせるもの(あるいは時空内の曲面)に対して, どのような絡み方の数学的な理論展開が可能だろうか?この質問に関する具体例として, 2節ではプリオン分子モデルについて, 3節では「こころ」のモデルについて, 理論展開を試みる. 結び目理論がいろいろなものに適用できる可能性を感じていただけたら幸いである.2. プリオン蛋白分子モデルの結び目理論蛋白分子はアミノ酸配列からなるひもと考えることができる. プリオンの異常による病気, プリオン病は, 牛ならば狂牛病, ヤギならばスクレイピー, ヒトならばクロイツフェルト・ヤコブ病などと呼ばれるが, 哺乳類すべてに同様な病気があるといわれている. プリオン病を引き起こす原因は不明となっているが, 1997年にノーベル医学・生理学賞を受賞したスタンレイ B. プリズナー理論では, プリオン蛋白分子の立体構造が引き起こす病気といわれている. 知られているプリオンタンパク分子の性質をここに挙げる.12)プリオン蛋白分子の性質:(1) 前駆的プリオン蛋白分子(図2.1)は, N-末端が失われて, 成熟型(正常型)プリオンPr PCまたは異常型プリオンPrP SCに変わる.(2) 成熟型プリオンPr PCと異常型プリオンPrP SCから2つの異常型プリオンPrP SCが生成される.(3) 成熟型プリオンPr PCと異常型プリオンPrP SCの1次構造は同じで, それらの主な違いは立体構造にある.(4) 成熟型プリオンPr PCのα-へリックスは, 異常型プリオンPrP SCでは, β-シートに変わっている.(5) 1か所S-S結合部がある.図2.1:前駆的プリオン蛋白分子 (山内・立石監修, スローウイルス感染とプリオン, 近代出版(1995)参照)前駆的プリオン蛋白分子は, 全体が井桁状に固定され, 両端も固定されているが, 成熟型プリオンPr PCと異常型プリオンPrP SCでは図2.1の上部(N末端)が取り除かれ, 特に異常型プリオンPrP SCではバラけている状態にある. 成熟型プリオンPr PCでも異常型プリオンPrP SCでもそうであるが, 下部(C末端)は細胞膜に錨を下ろす形で繋がっている. プリオンに関する結び目理論の問題として, 次の問題は興味深い問題といえよう.13)問題:プリオン蛋白分子は絡まりやすいか?図2.2:プリオンストリング図2.3:プリオンタングルを空間グラフと考えるプリオン蛋白分子のモデルとして, 1つの自明な結び目であるループ(S-Sループ)と1本のひも(GPIテイル)からなる空間グラフで, 3次元空間の下半空間(黒色部分)とつながったもの(プリオンストリング)を考える(図2.2参照). ここに注目する理由は,ここがプリオンコアに相当する部分であり, 感染価がプリオンコアの濃度と比例するなどプリオンコアに問題がありそうだからである. 図2.3左側の図のようないくつかのプリオンストリングの集まりをプリオンタングルという. それを数学的に扱うために図2.3右側の図のような空間グラフ(プリオングラフ)として考える. プリオンタングルが絡まることの意味をはっきりさせるために, つぎの概念を用意する.定義:プリオンタングルTがプリオンタングルT1とT2の分離和であるとは,Tをプリオングラフと考えたとき, それが平面によりT1とT2のプリオングラフに分けられていることである(図2.4参照). 分離可能プリオンタングルとは分離和に同型なプリオンタングルのことで, 分離不能プリオンタングルとは分離可能でないようなプリオンタングルのことである.図2.4例えば, 図2.3左側の図のプリオンタングルは分離可能である. 次のような分離不能プリオンタングルの存在は, 報告者の結果から示される.14)定理: 2つの任意の(分離可能あるいは分離不能)プリオンタングルT1とT2の分離和が与えられているとき, T1とT2に同型なものを合併したプリオンタングルT 1∪T2で, 分離不能になるようなものが無限個存在する. とくに,I型: T1あるいはT2に含まれるGPIテイルどうしの1回の交差交換II型: T1あるいはT2に含まれるGPIテイルとS-S ループの1回の交差交換のどちらの操作によっても, それらを構成できる(図2.6参照).図2.5:交差交換I型II型図2.6:分離不能プリオンタングルの例(II型は吉田佳代による)15)プリオングラフの分類問題は, 分類が実行可能に見える結び目理論の問題である.3. こころのモデルの結び目理論―こころの状態を図示する試みこころを結び目で図示してもよいのではないかと考えた理由として, 日常生活では, 性格・人格やこころのあり様をひもにたとえて表現しており, 経験上結び目で表現しても矛盾が生じにくい点を挙げることができる. 例えば, 素直な性格, ひねくれた性格, 思いの糸, こころがつながる, こころが固い絆で結ばれる, こころの琴線, 人間関係のもつれ, わだかまりが解ける, 人に絡む, …. 他にも, B. Stewartと P. G. Tait が1894に著した書物16) の中で“The soul exists as a knotted vortex ring in the aether. ”(魂はエーテル内の渦巻きの結び目として存在する)を主張したことも, こころを結び目で表現してもそう不自然ではないことを示唆している.17)結び目によるこころのモデルの基本的な考え方は, こころ(mind)を(これから定義するような)結び目とし, その結び目の型(つまり, 同型なものの集まり)を人格(personality)とする考え方である. 特に, その結び目が自明ならば素直な性格のこころ(untwisted mind), 自明でないならばひねくれた性格のこころ(twisted mind)と考える. さらに, その結び目の交差交換(図2.5)をこころ変わり(mind-change), 人格が変わるようなこころ変わりをこころの屈折(essential mind-change)と定義する.図3.1からわかるように, こころ変わりの仕方によって, 素直な性格のこころも, またひねくれた性格のこころも素直な性格のこころから生じることがわかる. この任意性は, 日々多尐のショックを受けてもひねくれないが, 何かをきっかけにひねくれるというこころのあり様を表現するのに適している.図3.1報告者は心理学の専門家ではなく, 榎本・桑原「人格心理学」放送大学教材(2004)で心理学を勉強した. それによると, 人格の基本因子は次のように定義される.18)人格の基本因子(1) 内向性‐外向性(2) 神経症的傾向(3) 精神病的傾向この項目(3)は曖昧さを含んでいるという理由から, 次に述べるような人格の5因子モデル(Five-Factor Model, Big Five)が提案された.19)人格の5因子モデル(1) 内向性-外向性(2) 神経症的傾向(3.1) 経験への開放性(3.2) 協調性(3.3) 誠実性5因子モデルについては, その心理テストが具体的な質問形式で一般的になされているものであり, こころのモデルの構成ではそのデータを利用する.20)こころのモデルを構成する際には, つぎの2点を解決しなくてはならない. (1)誕生時のこころの状態をどのように定義するか. 言い換えると, 両親から引き継がれた遺伝的性質により, 誕生時点で必ずしもこころが素直な性格のこころとは限らないこと(2)こころ変わりを起こすような年齢, 歴史, 標準化しえない要因による非常に多くの様々な原因があることさて, Kという人のn歳時のこころの結び目モデルの構成法を紹介しよう. まず以下の(ステップI)~(ステップV)のようにして, Kに関する5因子モデルの数値データを取得する. ここで, それぞれ因子について, -1は否定的性格, +1は肯定的性格であることを意味しており, Kの両親のデータは肯定的性格でも0とおく.ni=1 ni=1 ni=1 ni=1 ni=1(ステップI )K の誕生時の父親の数値データを取得する.(1)内向性-外向性: IE F = -1, 0(2)神経症的傾向: N F = -1, 0(3-1)経験への開放性: O F = -1, 0(3-2)協調性: A F = -1, 0(3-3)誠実性: C F = -1, 0(ステップII )K の誕生時の母親の数値データを取得する.(1)内向性-外向性: IE M = -1, 0(2)神経症的傾向: N M = -1, 0(3-1)経験への開放性: O F = -1, 0(3-2)協調性: A M = -1, 0(3-3)誠実性: C M = -1, 0(ステップIII )K の誕生時の両親のデータを計算する.-2≦IE P =IE F + IE M ≦ 0-2≦ N P = N F + N M ≦ 0-2≦ O P = O F + O M ≦ 0-2≦ A P = A F + A M ≦ 0-2≦ C P = C F + C M ≦ 0(ステップIV )K のi 歳時の5因子のデータの数値化する(i=1, 2,…, n). (1)内向性-外向性: IE i = -1, 0, 1(2)神経症的傾向: N i = -1, 0, 1(3-1)経験への開放性: O i = -1, 0, 1(3-2)協調性: A i = -1, 0, 1(3-3)誠実性: C i = -1, 0, 1(ステップV )K のn 歳までの5因子の数値の総和を求める.-2-n ≦IE P +∑ IE i ≦n-2-n ≦ N P +∑ N i ≦n-2-n ≦ O P +∑ O i ≦n-2-n ≦ A P +∑ A i ≦n-2-n ≦ C P +∑ C i ≦n(ステップV)の5因子それぞれの数値の総和と0を比較し, それらの小さい方をそれぞれ IE[n], N[n], O[n], A[n], C[n] で表し, n歳でのこころの結び目M(n;a,b) を次のように定義する.21)定義: n歳でのこころの結び目 M(n;a,b)とは, 図3.2のa+2b交差点を持つ図式の結び目のことである. ただし, a, b はa= IE[n] + N[n], b=O[n]+A[n]+C[n]で定義される整数である. このとき, a, bは -2n-4≦a≦0, -3n-6≦b≦0をみたす.図3.2例えば, M(n;-1,-1)は三葉結び目, M(n;-2,-1)は8の字結び目を表している. 次の命題は, 結び目理論の標準的な2橋結び目の分類理論から直ちに示すことができる.22)命題:(1)こころの結び目M(n;a,b) が素直な性格のこころの結び目である必要十分条件は, a=0 または b=0となることである.(2)ひねくれた性格のこころの結び目M(n;a,b)とM(m;c,d)が同じ人格をもつ必要十分条件は, (a,b)=(c,d)となることである.我々のこころの遍歴は, このようなこころの結び目モデルの場合, 誕生時から死亡時までの時空にはめ込まれたシリンダー状の曲面になる(図3.3参照). このシリンダーは有限個の自己交差点をもつが, それらはこころ変わりを起こしている点(人格が変わるときには屈折点)を表していることになる.図3.3:こころの遍歴このようなこころの結び目モデルを使えば, (n人の)こころの絡み目も考えることができ, その心的関係も図示できることになる. ここでは,こころの絡み目の自己救済関係の分類について説明しよう. こころの結び目成分Kとこころの絡み目成分Lからなるこころの絡み目K∪Lを考えるとき, KとLが分離可能であるとは, 絡み目K∪Lの任意の図式が, ライデマイスター移動により, K と Lが交叉しない位置にまで移動できることである. また, Kが Lから自己救済可能であるとは, Kの何回かのこころ変わりにより, K と L は分離可能になることである. 問題を単純化するために次のような同値関係を導入する.定義:こころの絡み目L と L’が類似の自己救済関係をもつとは, 結び目成分に関する全単射対応τ:L → L’で, つぎをみたすようなものが存在することである:すなわち, Lの任意の結び目成分 K とそれ以外のLの成分からなる任意の部分絡み目 S について, つぎの(1)と(2)が成り立つ.(1) K と S が分離可能であるかどうかとτ(K)とτ(S)が分離可能かどうかが一致する.(2) K が S から自己救済であるかどうかということとτ(K)がτ(S)から自己救済可能であるかどうかということが一致する.そこで, n人のこころの絡み目の自己救済関係とは, 類似の自己救済関係をもつものを無視したときのn人のこころの絡み目のことである, と定義すれば, 次の問題が自然に思い浮かぶ.問題: n人のこころの絡み目の自己救済関係を分類して図示せよ.分離可能なn人のこころの絡み目の自己救済関係を代表する絡み目は定義により必ず分離可能であるので, この問題を考えるには分離不能なn人のこころの絡み目の自己救済関係のみを考えればよい. 分離不能な2人のこころの絡み目の自己救済関係はつぎのようになる.命題:分離不能な2人K1, K2のこころの絡み目の自己救済関係は, 図3.4の(1),(2), (3)に示される3つの絡み目で代表される. ここで, (1)は両方が互いに他者から自己救済不可能であること, (2)は両方が互いに他者から自己救済可能であること, (3)は K1がK2から自己救済可能であるが, K2がK1から自己救済不可能であることを意味している. 特に(3)が起こる場合には, 必ずK1はひねくれた性格のこころである.図3.43人以上のこころの絡み目の自己救済関係の分類は大変複雑になる. その理由の1つとして, 図1.3のボロミアン環のような, どの2人のこころの結び目も分離しているが, 全体として分離不能になっているようなこころの絡み目の存在を挙げることができる. ここでは, 分離不能な3人のこころの絡み目の自己救済関係(いわゆる三角関係)は, このような1対2の自己救済関係を無視しても, 30通りに分類されることを示唆するにとどめる.23)4. まとめ1節では, 森羅万象の基本に結び目あり, ひもとみなせるものがあればそこでは結び目理論が展開可能ではないか、という自説の説明を試みた. 2節では, プリオン分子の結び目論的モデルを, 3節では心理学の「こころ」の結び目論的モデルを解説した.24)注1)結び目理論の一般的な事柄については, 拙書「レクチャー結び目理論」(2007)共立出版,あるいはそこで述べた参考書などを参照されたい.2) 実際のサイエンスにおいて, 端点付き結び目・絡み目や次数1の頂点付き空間グラフの絡まりが意味を持つ場合があり, そのような場合の研究にも報告者は興味を持っている.拙著,in: Knots and soft-matter physics, Topology of polymers and related topics in physics, mathematics and biology, 物性研究 92-1(2009-4),16-19では, 端点付き結び目・絡み目や次数1の頂点付き空間グラフを結び目理論の対象とする研究を行った. 3)表の中程の3つの結び目を除き, すべての結び目の交差点の上下を区別せず描いてある.その理由は, それらは交代結び目といわれるもので, 交差点の上下を1か所指定し, そこからひもに沿って上下を交代に付けていけば, 鏡像であるものを無視して一意的に結び目が復元できるからである.4) 北海道恵庭市発掘調査報告書「北海道恵庭市ユカンボシE8遺跡B地点」(1992)参照.5) L. H. カウフマン「結び目の数学と物理」培風館, 1995(鈴木・筆者監訳)や注1)の拙書で述べた参考書などを参照されたい.6) E. J. Wasserman et al, J. Am. Chem. Soc. 82(1960), 4433-4434を参照せよ.7) J. P. Sauvage et al., Angew. Chem. Int. Ed. Engl. 43(2004), 4482を参照せよ.8) J. F. Stoddart et al. Science 304(2004), 1308を参照せよ.9) A. Harada; J. Li; M. Kamachi, Nature 356(1992), 325-327を参照せよ.10) 手塚,他「トポロジーデザイニング-新しい幾何学からはじめる物質・材料設計」エヌ・ティー・エス(2009)を参照されたい.11) /edr/jp/astro/structures/structures.aspなどを参照せよ.12) K. Basler et al., Cell 46(1986), 417-428, Z. Huang et al.,Proc. Natl. Acad. A.91(1994), 7139-7143, 山内・立石監修「スローウイルス感染とプリオン」近代出版(1995),「狂牛病のすべてファクト・ブック」日経BP社(1996 )などを参照されたい.13) 異常プリオンからアミロイド線維というものが形成される. 前駆アミロイドベータ蛋白質の断片の蓄積で起こる病気であるアルツハイマーについても, それらの断片からアミロイド線維が形成されることが知られている. 結び目理論からのアプローチの方法として, 蛋白分子のモデルを構成してその絡まり方を研究することが考えられるだろう.14) 前半の結果はより一般的な形で拙著, Osaka J. Math. 26(1989),743-758で示されている.交差交換の条件を課した結果は拙著,in: Knots 90, Walter de Gruyter(1992), 465-476で暗に示されている. 拙著,in:Topological Molecules, Proc. of Yamada Conference 2008(出版予定), (http://www.sci.osaka-cu.ac.jp/~kawauchi/index.html)を参照されたい. ついでながら, 1つのプリオンストリングのみでは, 条件なしにはどれも自明なプリオンストリングに同型になってしまう. 一方, S-SループがGPIテイルの結び目についてロタキサンのストッパーのように働く場合には,1つのプリオンストリングでも自明なプリオンストリングに同型にならないようなものを構成できる.15) 吉田著,2009年度大阪市立大学修士論文を参照せよ.16)R.Rucker,The fourth dimension,A guided tour of the higher universes,Houghton Mifflin Company, Boston (1984) を参照せよ. この説はKelvin卿(= W.Thomson)の渦巻き原子説に基づく. P.G. Tait は結び目理論研究の先祖の1人である.17) この講演の翌日, 山下靖氏(奈良女子大)からある本の存在を教わった. それは, フランスの精神分析医で思想家のジャック・ラカンが曲面(メビウスの帯, トーラス, クロスキャップ, クラインの壺)およびボロミアン環を心的構造の対象として取り上げていたことを記したジャンヌ・グラノン‐ラフォン著「ラカンのトポロジー, 精神分析空間の位相構造」(中島・吉永訳), 白揚社(1991)の本のことである. 内容は本報告とは一致しないが,この本から心的構造と曲面のトポロジーとは相性がよいこと, および本報告でも意味を持つボロミアン環がラカンの心的構造として意味があることを読み取ることができ, こころを結び目で表現する研究をさらに深化させるのに参考になる.18) H. J. Eysenck, The biological basis of personality, Transaction Publishers(2006) を参照せよ.19) P. T. Costa and R. R. McCrae,Journal of Personality and Social Psychology, 55(1988), 258-265 を参照せよ.20) この報告では 5因子モデルから構成できるもっとも単純なモデルを紹介している. 拙著,in: Proc. Knot theory for Scientific Objects, OCAMI Studies, 1(2007), 129-141において構成したものとは尐しだけ異なる.21) 図3.2において, 2bの代わりにbとおくと, a, bの値により結び目あるいは2成分絡み目となる. そのときには「こころ変わり」を交差交換によっては定義できないが, 結び目理論のスプライスの概念(例えば, 注1)で述べた拙書を参照)を利用すれば類似の考察が可能である.22) 注1)で述べた拙書を参照されたい.23)命題の証明も含めて, 注20)で述べた拙著を参照されたい.24)「こころ」を国と解釈すれば, 国と国の関係も絡み目として表せるだろう. オリンピック・マークを想起されたい.。
「子どもが育つ魔法の言葉」ドロシー・ロー・ノルト、レイチャル・ハリス( 原題Children Learn What They Live Parenting to Inspire Values) 詩「子は親の鏡」けなされて育つと、子どもは、人をけなすようになるとげとげした家庭で育つと、子どもは、乱暴になる不安な気持ちで育てると、子どもも不安になる「かわいそうな子だ」と言って育てると、子どもは、みじめな気持ちになる子どもを馬鹿にすると、引っ込みじあんな子になる親が他人を羨んでばかりいると、子どもも人を羨むようになる叱りつけてばかりいると、子どもは「自分は悪い子なんだ」と思ってしまう励ましてあげれば、子どもは、自信を持つようになる広い心で接すれば、キレる子にはならない誉めてあげれば、子どもは、明るい子に育つ愛してあげれば、子どもは、自分が好きになる認めてあげれば、子どもは、自分が好きになる見つめてあげれば、子どもは、頑張り屋になる分かち合うことを教えれば、子どもは、思いやりを学ぶ親が正直であれば、子どもは、正直であることの大切さを知る子どもに公平であれば、子どもは、正義感のある子に育つやさしく、思いやりをもって育てれば、子どもは、やさしい子に育つ守ってあげれば、子どもは、強い子に育つ和気あいあいとした家庭で育てば、子どもは、この世の中はいいところだと思えるようになるけなされて育つと、子どもは、人をけなすようになる∙不満だらけの親の気持ちは、ものの言い方や、ちょっとした仕草や目つきに表れます。
相手に不満があるときには、自然に目つきや物言いがきつくなるものです。
小さな子どもは、こういう親の態度にとても敏感で、傷つきやすいものです。
∙子どものためにはならないと分かっていても、わたしたちは、ついカッとなってしまうものです。
カッとならないためには、意識的に気持ちをコントロールしなくてはなりません。
事前に段取りをとっておき、やっていいことといけないことを子どもに言い聞かせておけば、避けられることもあります。
出会った人を必ず味方にする「フレーム理論」プレジデント2014/8/19 09:15日本大学教授佐藤綾子=文■まずは自己分析。
アピールするポイントを定めるこの連載では、たびたびにわたり「パフォーマンス心理学」の技法は「相手に自分のことを上手に伝える」うえで非常に有効である、ということをお伝えしてきました。
今回はその総仕上げとして、パフォーマンス心理学の原理原則であり、出会った人を必ず自分の味方にしてしまう、強い自己アピールの仕方をご紹介します。
それは「フレーム理論」です。
「フレーム」とは額縁、枠組みです。
モナリザの絵を思い出してください。
ルーブル美術館で観るとわかりますが、モナリザは意外に小さいのです。
もしあの絵が額縁なしで、そのまま廊下にピンナップされていたら、人々の注目を集めるには時間がかかってしまうことでしょう。
人は皆、フレームに収められたところだけに注目し、フレームの外は忘れてしまいがちです。
人間には、そんな受け止め方の傾向があるのです。
それを利用したのが、パフォーマンス心理学の「フレーム理論」。
あなたが持っている長所や実力の中で、特に強調して見せたいと思う部分をフレームに入れてクローズアップし、あとの部分はちょっとフェードアウトしておくことです。
相手はまず、あなたがクローズアップしたフレームの中だけを、強いインパクトで受け止めます。
そこで注意したいのが、フレームに入れるということは、自分にとって長所でもない部分をアピールしたり、不相忚な実力があるように見せたりすることではない、ということです。
例えばあなたが、判断力は人並みで、協調型の人間だったとしましょう。
ただ、新たに会うクライアントには、自分の中のありったけの決断力を最大限にアピールしたい。
そんなときには、髪形をビシリと決め、キリッと口元も引き締め、アイコンタクトを最大に。
声のトーンは、文末を「……」と尻切れトンボで終わらせずに完結させ、イントネーションも下降調で区切ります。
日本労働組合日本の場合、複数の労働者が組合結成に合意することにより労働組合を結成できる。
結成についていかなる届け出も認証も許可も必要ではない。
ただし、法人登記を行うためには、地域の労働委員会に規約その他必要書類を提出し、労働組合法上の規定を満たしている証明を得る必要がある。
定義労働組合とは、賃金労働者が、その労働生活の諸条件を維持または改善するための恒常的な団体である日本の労働組合法では、その第2条で「……労働者が主体となつて自主的に労働条件の維持改善その他経済的地位の向上を図ることを主たる目的として組織する団体又はその連合団体をいう」と定義している。
労働組合は、職業別組合から出発し、一般組合を経て産業別組合へと発展していくのが、多くの先進工業国でみられた展開過程であった。
ただし日本においては、職業別組合から企業別組合へという過程が特徴的である。
日本最初の労働組合は、アメリカ合衆国で近代的な労働組合運動を経験した高野房太郎や片山潜らによって1897年に結成された職工義友会を母体に、同年7月5日に創立された労働組合期成会である。
現在のような企業別組合が発達したのは、第二次世界大戦以降である。
労働組合員および労働組合のシンパに対しては、経営者にとって不都合な場合が多いため「共産主義者」「アカ」などのレッテル貼りがおこなわれ、時折職場でのイジメが問題となる場合がある。
実際には資本主義経済のなかで自身の労働に対する取り分を主張しているだけであり、サラリーマンを中心とした労働者は給与賃金に対する主張を行うためにも労働組合を利用すべきである、という意見もみられる。
労働者労働者とは、労働基準法第9条で「職業の種類を問わず、事業又は事務所に使用される者で賃金を支払われるものをいう」とされる。
契約上において、請負、個人事業主とされている者についても、実質的な「使用従属関係の有無」で判断される。
(厚生労働省労働基準局の通達を参照すること。