岩土力学中应力计算

第四章地基土中的应力计算★概述★土中自重应力计算★基底压力的分布与计算★地基附加应力及有效应力原理第一节概述地基应力计算的目的：1. 计算土体变形，比如建筑物地基的沉降；2. 土体承载力与稳定性分析。

一、地基土中应力分类1.按引起的原因分为自重应力和附加应力自重应力——由土体自身重量所产生的应力。

附加应力——由外荷（静的或动的）引起的土中应力增量。

一、地基土中应力分类2.按作用原理或应力传递方式分为有效应力和孔隙应（压）力有效应力——土粒所传递的粒间应力，它是控制土的体积（或变形）和强度两者变化的土中应力。

孔隙应（压）力——由土孔隙中的水和气体所传递的应力。

二、基本假设视地基土体为连续体半无限的线弹性体均质各向同性体按《弹性力学》的方法进行计算。

三、土中一点的应力状态土中一点的应力状态：---土中一点在各个方向上应力的数值。

三、土中一点的应力状态土力学中，法向应力以压应力为正，拉应力为负。

剪应力的正负号规定是：当剪应力作用面上的法向应力方向与坐标轴的正方向一致，则剪应力的方向与坐标轴正方向一致时为正，反之为负。

第二节自重应力的计算一、均质土体1.竖向自重应力2.水平向自重应力K 0-土的静止侧压力系数z FFz cz γγσ=•=二、成层土体地基为不同土层且无地下水ii h γσ∑=三、有地下水时的自重应力地下水位以下的砂土、粉土以及粘性土液性指数大于等于1时均取浮重度；粘性土液性指数小于等于0时取天然重度，在0～1之间时依最不利原则取其天然或浮重度。

例题4-1、4-2、4-3例题4-3两者相比较可以看出，当地下水位下降时，会引起有效自重应力的增加。

地下水位的升降，使地基土中自重应力也相应发生变化。

当地下水位长期下降时，地基中有效应力增加，从而引起地面大面积沉降；当地下水位长期上升时，会引起地基承载力减少、湿陷性土的塌陷等现象。

第三节基底压力和基底附加压力计算地基---建筑物影响范围内的有限土层。

第2章 土中 应 力 计 算自重应力：由土体重力引起的应力附加应力：由于建筑物荷载在土中引起的应力 要求：正确理解自重应力、附加应力、基底压力、基底附加压力的概念及影响因素。

掌握各种应力的计算公式、计算方法及分布规律。

第一节 土中应力状态法向应力以压应力为正，拉应力为负；剪应力以逆时针方向为正，顺时针方向为负。

σx 、σy 、σz ，τxy=τyx、τyz=τzy、τzx=τxz，第二节 土中的自重应力由土体重力引起的应力称为自重应力。

一般是自土体形成之日起就产生于土中。

一、均质地基土的自重应力土体在自身重力作用下任一竖直切面均是对称面，切面上都不存在切应力。

因此只有竖向自重应力σc z ，其值等于单位面积上土柱体的重力W 。

深度z 处土的自重应力为： 式中 γ为土的重度，kN/m 3 ；F 为土柱体的截面积m 2。

σcz 的分布:随深度z 线性增加，呈三角形分布。

二、成层地基土的自重应力地基土通常为成层土。

当地基为成层土体时，设各土层的厚度为h i ，重度为γi ，则在深度z 处土的自重应力计算公式地下水位以上的土层取天然重度γ，地下水位以下的土层取有效重度γ`( γ` = γsat- γw) γw=10kN/m3 三、土层中有不透水层时的自重应力在地下水位以下，如果埋藏有不透水层（坚硬的粘土、基岩），该层面处的自重应力应按上覆土层的水土总重计算。

四、水平向自重应力式中K 0为侧压力系数，也称静止土压力系数例题 2-1某土层及其物理性质指标如图所示，地下水位在地表下1.0 m ，计算土中自重应力并绘出分布a 点：b 点：c 点：d 点：例题 2-2某地基土层的地质剖面如图所示，计算各土层的自重应力并绘出分布 50m 处：48m 处：45m 顶：45m 不透水层面：43m 处：【课堂讨论】• 土的性质对自重应力有何影响?• 地下水位的升降是否会引起土中自重应力的变化？如何影响？作业1、20==h cz γσkpa h cz 6.1816.1811=⨯==γσkpa h h cz 4.271)108.18(6.182211=⨯-+=+=γγσkpah h h cz 6.523)104.18(4.27332211=⨯-+=++=γγγσ0==h cz γσkpah cz 3621811=⨯==γσh h cz 5.613)105.18(362211=⨯-+=+=γγσkpah h h ww cz 5.913105.612211=⨯+=++=γγγσkpah h h h w w cz 5.1292195.91332211=⨯+=+++=γγγγσ第二节 基底压力的简化计算建筑物荷载通过基础传递给地基的压力称基底压力，又称地基反力。

第五章 土体中的应力计算第一节 概述大多数建筑物是造建在土层上的，我们把支承建筑物的这种土层称为地基。

由天然土层直接支承建筑物的称天然地基，软弱土层经加固后支承建筑物的称人工地基，而与地基相接触的建筑物底部称为基础。

地基受荷以后将产生应力和变形，给建筑物带来两个工程问题，即土体稳定问题和变形问题。

如果地基内部所产生的应力在土的强度所允许的范围内，那么土体是稳定的，反之，土体就要发生破坏，并能引起整个地基产生滑动而失去稳定，从而导致建筑物倾倒。

地基中的应力，按照其因可以分为自重应力和附加应力两种：自重应力：由土体本身有效重量产生的应力称为自重应力。

一般而言，土体在自重作用下，在漫长的地质历史上已压缩稳定，不再引起土的变形（新沉积土或近期人工充填土除外）。

附加应力：由于外荷（静的或动的）在地基内部引起的应力称为附加应力，它是使地基失去稳定和产生变形的主要原因。

附加应力的大小，除了与计算点的位置有关外，还决定于基底压力的大小和分布状况。

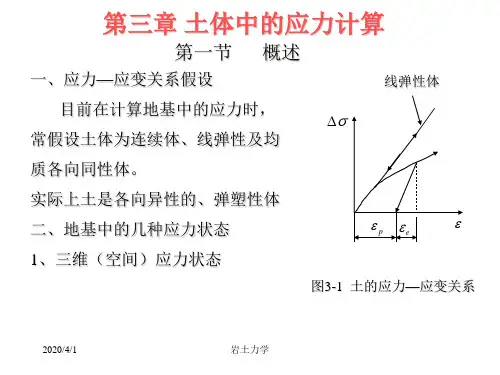
一、应力～应变关系的假定真实土的应力～应变关系是非常复杂的，目前在计算地基中的附加应力时，常把土当成线弹性体，即假定其应力与应变呈线性关系，服从广义虎克定律，从而可直接应用弹性理论得出应力的解析解。

1、关于连续介质问题弹性理论要求：受力体是连续介质。

而土是由三相物质组成的碎散颗粒集合体，不是连续介质。

为此假设土体是连续体，从平均应力的概念出发，用一般材料力学的方法来定义土中的应力。

2、关于线弹性体问题理想弹性体的应力与应变成正比直线关系，且应力卸除后变形可以完全恢复。

土体则是弹塑性物质，它的应力应变关系是呈非线性的和弹塑性的，且应力卸除后，应变也不能完全恢复。

为此进行假设土的应变关系为直线，以便直接用弹性理论求土中的应力分布，但对沉降有特殊要求的建筑物，这种假设误差过大。

3、关于均质、等向问题理想弹性体应是均质的各向同性体。

而天然地基往往是由成层土组成，为非均质各向异性体。

岩土水平抗力系数的解析与应用岩土水平抗力系数是岩土力学中的一个关键参数，它对于岩土工程设计和施工具有重要意义。

本文将对岩土水平抗力系数进行解析和应用，帮助您更好地理解和应用这一概念。

一、岩土水平抗力系数概述在岩土工程中，土体或岩体受到外部作用力时，会产生一定的抗力。

岩土水平抗力系数描述了土体或岩体在水平方向上抵抗外部荷载或应力的能力，它是反映岩土抗剪强度的一个重要参数。

岩土水平抗力系数可以用于计算基坑、挡墙、地基承载力、边坡稳定性等方面的设计。

二、岩土水平抗力系数的计算方法岩土水平抗力系数的计算方法有很多，常用的方法有承载力法、基于土壤参数的方法和基于随机场理论的方法等。

以下是一种常用的计算方法：1. 承载力法承载力法是基于限 equilibrium 原理，即在岩土体中的任何一个平面上，切片的抗剪力不超过该平面上的抗剪强度，抗剪强度可用库仑公式表示。

根据承载力法，水平抗力系数可通过以下公式计算：Kh = τ / (γ * H)其中，Kh表示水平抗力系数，τ表示土体或岩体的抗剪强度，γ表示土体或岩体的体积重量，H表示土体或岩体的高度。

2. 基于土壤参数的方法基于土壤参数的方法是通过实验室试验和现场测试获取土体参数，然后根据经验公式计算水平抗力系数。

这种方法广泛应用于土体工程领域。

3. 基于随机场理论的方法在某些情况下，土壤的物理性质可能是非均匀和随机变化的，此时可以考虑使用基于随机场理论的方法来计算水平抗力系数。

这种方法可以更准确地描述土体的非均匀性和变异性。

三、岩土水平抗力系数的应用岩土水平抗力系数在岩土工程设计和施工中有着广泛的应用。

以下是几个常见的应用方面：1. 基坑设计在基坑设计中，需要考虑土壤的水平抗力系数，以确定基坑支护结构的类型、尺寸和稳定性。

水平抗力系数的大小直接影响基坑支护的安全性和经济性。

2. 边坡稳定性分析边坡稳定性是岩土工程中的关键问题之一，水平抗力系数是边坡稳定性分析的基础。

土力学2地基中应力计算土力学是研究土体力学性质的科学分支，其中地基中应力计算是土力学中的一个重要内容。

地基是建筑物的基础，承受着建筑物的重量和外部荷载的作用。

合理计算地基中的应力，对设计和施工都至关重要。

本文将介绍地基中应力计算的基本原理和方法。

地基中的应力可以分为两种类型：垂直应力和水平应力。

垂直应力是指垂直于地面方向的应力，也称为轴向应力。

水平应力是指平行于地面方向的应力，也称为环向应力。

地基的应力状态主要由建筑物的重力作用和地基外荷载共同决定。

首先要进行地基中垂直应力的计算。

垂直应力可以通过建筑物的重量和地基的承载力来计算。

一般情况下，建筑物的重量可以根据结构设计文件中的荷载参数进行估算。

而地基的承载力则需要根据土壤的性质和地基的几何形状来进行计算。

常用的计算方法有承载力极限平衡法和桩基承载力计算法。

通过这些方法可以计算出地基中的垂直应力分布。

接下来是地基中水平应力的计算。

水平应力的计算与地基的变形特点相关。

常见的地基变形包括沉降、倾斜和水平位移等。

根据土壤的弹性模量、剪切模量和地基的几何形状，可以利用弹性力学原理推导出地基中的水平应力。

对于直角边界条件的地基来说，可以通过弹性基础解法来进行计算。

而对于其它边界条件下的地基，需要使用有限元软件进行数值计算。

在进行地基中应力计算时，还需要考虑土体的强度特性。

土体的强度主要包括抗压强度、抗剪强度和抗拔强度等。

这些强度参数可以通过室内试验或现场试验来测定。

在计算地基中的应力时，需要按照土体的强度特性来确定土体的极限承载力和变形特性。

除了垂直应力和水平应力的计算，地基中的应力计算还需要考虑地下水的影响。

地下水可以对地基的应力产生很大的影响，特别是在饱和土的情况下。

地下水压力可以通过水文地质调查和现场测试来进行测定，并考虑到地基中的应力计算中。

总之，地基中应力的计算对于设计和施工都至关重要。

它直接影响到地基的稳定性和建筑物的安全性。

因此，在进行地基设计时，需要进行合理的应力计算，并结合实际情况进行工程应用。

土木工程师-专业基础（水利水电）-岩土力学-土的应力分布及计算[单选题]1.一地基中粉质黏土的重度为16kN/m3，地下水位在地表以下2m的位置，粉质黏土的饱和重度为18kN/m3（江南博哥），地表以下4m深处的地基自重应力是()。

[2017年真题]A.65kPaB.68kPaC.45kPaD.48kPa正确答案：D参考解析：自重应力计算公式为：σ＝γz。

式中，z为土层厚度；γ为土体重度。

计算时地下水位以上用天然重度，地下水位以下用有效重度（浮重度），即：γ′＝γsat－γw。

式中，γsat为粉质黏土的饱和重度；γw为水的重度。

故可得：γ′＝18－10＝8kN/m3，代入数据得：σc＝γh1＋γ′h2＝16×2＋8×2＝48kPa。

[单选题]2.引起土体变形的力是()。

[2013年真题]A.总应力B.有效应力C.孔隙水压力D.自重应力正确答案：B参考解析：有效应力是指通过颗粒接触点传递的力，直接与土的变形和强度相关，定义为饱和土体单位截面上由土颗粒承担的力。

对于饱和土体，可以推出土体中的总应力σ等于有效应力σ′与孔隙水压力u之和，即σ＝σ′＋u。

其中，有效应力决定着土体的变形和强度，一般需利用有效应力原理，通过确定总应力和孔隙水压力间接确定。

[单选题]3.均布载荷作用下，矩形基底下地基中同样深度处的竖向附加应力的最大值出现在()。

[2016年真题]A.基底中心以下B.基底的角点上C.基底点外D.基底中心与角点之间正确答案：A参考解析：当矩形基础底面受到竖直均布荷载作用时，基础的四个角点下任意深度z处的竖向附加应力均相同，计算公式为：σz＝Kcp0。

式中，p0表示基底附加压力，单位为kPa；Kc表示无因次附加应力系数。

对于非角点下地基中的应力可用角点法求得，即自计算点将荷载面分割为几个小矩形荷载面，计算点要位于各小荷载面的公共角点上，再利用角点公式计算各个小荷载面对计算点产生的附加应力，然后叠加。

第三章土体中的应力计算学习指导内容简介建筑物的建造使地基土中原有的应力状态发生了变化，如同其它材料一样，地基土受力后也要产生应力和变形。

在地基土层上建造建筑物，基础将建筑物的荷载传递给地基，使地基中原有的应力状态发生变化，从而引起地基变形。

研究地基土中应力的分布规律是研究地基和土工建筑物变形和稳定问题的理论依据，它是地基基础设计中的一个十分重要的问题。

教学目标掌握土中自重应力计算、基底压力计算以及各种荷载条件下的土中附加应力计算方法。

学习要求1、掌握土中自重应力计算2、掌握矩形面积均布荷载、矩形面积三角形分布荷载以及条形荷载等条件下的土中竖向附加应力计算方法3、掌握基底压力和基底附加压力分布与计算4、掌握太沙基的饱和土体的有效应力原理要点及完整表达式5、了解有效应力原理的工程应用基本概念自重应力、附加应力、有效应力、孔隙水压力、基底压力、基底附加压力、角点法、附加应力系数学习内容第一节概述第二节有效应力原理第三节地基中的自重应力第四节基底附加压力第五节地基中附加应力第六节应力路线学时安排本章总学时数：12学时第一节0.5学时第二节3学时第三节0.5学时第四节2学时第五节 3.5学时第六节 1.5主要内容第一节概述大多数建筑物是造建在土层上的，我们把支承建筑物的这种土层称为地基。

由天然土层直接支承建筑物的称天然地基，软弱土层经加固后支承建筑物的称人工地基，而与地基相接触的建筑物底部称为基础。

地基受荷以后将产生应力和变形，给建筑物带来两个工程问题，即土体稳定问题和变形问题。

如果地基内部所产生的应力在土的强度所允许的范围内，那么土体是稳定的，反之，土体就要发生破坏，并能引起整个地基产生滑动而失去稳定，从而导致建筑物倾倒。

地基中的应力，按照其因可以分为自重应力和附加应力两种：自重应力：由土体本身有效重量产生的应力称为自重应力。

一般而言，土体在自重作用下，在漫长的地质历史上已压缩稳定，不再引起土的变形（新沉积土或近期人工充填土除外）。

地层破裂压力计算公式地层破裂压力相关计算公式地层破裂压力是地层中发生裂缝或破裂的临界应力值，是岩土力学中的一个重要参数。

本文将列举几个与地层破裂压力相关的计算公式，并举例解释说明。

1. 维里准则(Von Mises Criterion)维里准则是地层破裂压力计算中常用的一个准则，其公式如下：维里应力= √[(σ₁ - σ₂)² + (σ₂ - σ₃)² + (σ₃ - σ₁)² + 6(τ₁₂² + τ₂₃² + τ₃₁²)]/ √2其中，σ₁、σ₂和σ₃为主应力，τ₁₂、τ₂₃和τ₃₁为主应力之间的切应力。

例子：假设某地层的主应力大小分别为σ₁ = 20 MPa，σ₂ = 15 MPa，σ₃ = 10 MPa，切应力大小分别为τ₁₂ = 5 MPa，τ₂₃ = 2 MPa，τ₃₁ = 3 MPa。

按照维里准则计算地层破裂压力：维里应力= √[(20 - 15)² + (15 - 10)² + (10 - 20)² + 6(5² + 2² + 3²)] / √2 = √[5² + 5² + (-10)² + 6(25 + 4 + 9)] /√2 = √[100 + 100 + 100 + 6(38)] / √2 = √[100 + 100 + 100 + 228] / √2 = √528 / √2 ≈ MPa因此，该地层的维里应力约为 MPa。

2. 摩尔—库伦准则(Mohr-Coulomb Criterion)摩尔—库伦准则是另一种常用的地层破裂压力计算准则，其公式如下：摩尔应力= (σ₁ - σ₃) / 2 + √[((σ₁ - σ₃) / 2)² + τ²]其中，σ₁和σ₃为主应力，τ为主应力之间的切应力。

例子：假设某地层的主应力大小分别为σ₁ = 20 MPa，σ₃ = 10 MPa，切应力大小为τ = 5 MPa。