当前位置：文档之家 › 数字信号处理第一章习题答案

数字信号处理第一章习题答案

  • 格式：pdf
  • 大小：3.19 MB
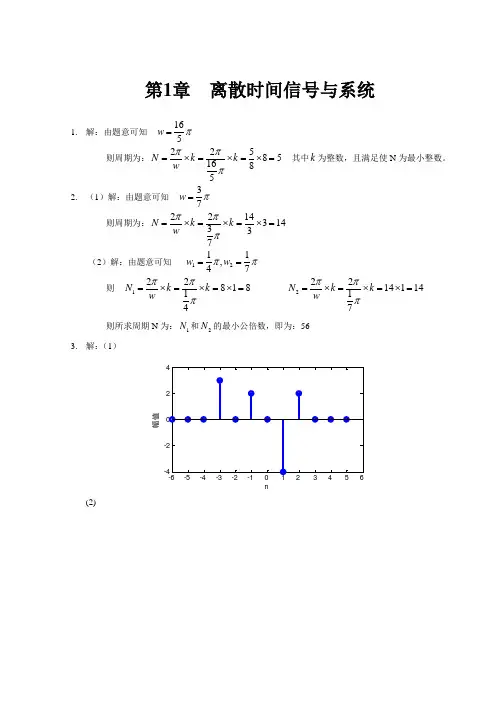
  • 文档页数：21

下载文档原格式

  / 21

合集下载

数字信号处理第一章课后答案

数字信号处理第一章课后答案
故系统是线性系统。
第 1 章 时域离散信号和时域离散系统
n
（7） y(n)= x(m) 令输入为m0
x(n－n0)
输出为
n
y′(n)= =0[DD)]x(m-n0)
m0
nn0
y(n－n0)= x(m)≠y′(n) m0
故系统是时变系统。 由于
n
T［ax1(n)+bx2(n)］=
［ax1(m)+bx2(m)
第 1 章 时域离散信号和时域离散系统
解：
x(n)=δ(n+4)+2δ(n+2)－δ(n+1)+2δ(n)+δ(n－1)
+2δ(n－2)+4δ(n－3)+0.5δ(n－4)+2δ(n－6)
2． 给定信号：
2n+5
－4≤n≤－1
(x(n)= 6 0
0≤n≤4 其它
(1) 画出x(n)序列的波形， 标上各序列值；
（2） y(n)=x(n)+x(n+1)
n n0
（3） y(n)= x(k) k nn0
（4） y(n)=x(n－n0) （5） y(n)=ex(n)
第 1 章 时域离散信号和时域离散系统
解：（1）只要N≥1， 该系统就是因果系统， 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M， 则|y(n)|≤M， （2） 该系统是非因果系统， 因为n时间的输出还和n时间以 后（（n+1）时间）的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
第 1 章 时域离散信号和时域离散系统 题2解图（四）

数字信号处理课后答案

数字信号处理课后答案

k = n0
∑
n
x[ k ]
（B） T {x[n]} =
∑
x[k ]
（C） T {x[ n]} = 0.5
x[ n ]
（D） T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ，输出为 y[n] ，满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ，则系统是（A） （A）线性的 （B）时不变的 （C）因果的 （D）稳定的 解：
（a） T { x[ n ]} = h[ n] + x[ n ], （c） T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ，单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 ， n < 0 ， 则 y[3] = 0.5 。 解： y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解： （a）
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞

数字信号处理第一章答案 朱冰莲

数字信号处理第一章答案 朱冰莲

1-3 （1）解：05162/2/85 ,16ππωπ==∴是周期的周期为。

（2）解：80()() 2 /16, n j x n eT ππωπ-==∴是无理数是非周期的。

（3）解：0382/2/43,8ππωπ==∴是周期的周期为。

1-4()()()()00000000112120()()*()()(),()0(2)1, ()()()1,()1,(m nm n n nnnmm n n m n nm n m n n n n n n n n n n n n n y n x n h n x m h n m n n y n n n n N y n x m h n m y n n n βαββααβααβαβαβααβαβαβαα∞=-∞=----==+--+--+--==-<=≤≤+-=-==-=--=≠-=+-=∑∑∑∑(1)当时当时部分重叠)β()()()()()00-N 11111-12(3)1 ,()()().,1(),nm n n n nnm m n n m n nm n N m n N n N n N N n n n n n N n n n n n N y n x m h n m y n N βαββααβααβαβαβαβαβαβαβααβ=+----=-+=-+-++--+---≥+-=-==--==≠--==∑∑∑当时全重叠1-6[]1212120000()()[()()()()][()][()][()]()()()()()|x(n)|<=M y(n)|=|x(n)g(n)|<x T ax n bx n ag n x n bg n x m aT x n bT x n T x n n g n x n n g n n x n n x n +=+=+∴-=-≠--（1）解：y(n)=g(n)(n)系统是线性系统。

因此是移变的由于n 时刻的系统的输出只和n 时刻信号有关因此是因果的当输入x(n)满足是对应的输出|=M |()|()g n g n 因此若为有限信号则系统稳定，否则不稳定[]0012121212()()[()()]()()[()][()]nnnm n k n k n T ax n bx n ax m bx m ax k bx k aT x n bT x n ===+=+=+=+∴∑∑∑（2）解：系统是线性系统。

数字信号处理(吴镇扬)第一章习题解答

数字信号处理(吴镇扬)第一章习题解答
傅立叶系数
提示：与理想采样信号的频谱进行比较。上述过程是物理采样后的频谱。
1.6解：
(1) （性质1）
(2) （性质4）
(3)
(4)1.7（1）Fra bibliotek：(2)解：
(3)解：
(4)解：
（5）解:
1.8 (1)解：令
由题意可知，所求序列等效为 。
而
故：
（2）解：
因为：
所以,
1.10 (1)解：
，为双边序列
本小题采用部分分式法求逆Z变换，可以使用“留数法”…..
所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
(3) 当n0＞0时，该系统是因果系统；当n0＜0时，该系统是非因果系统；系统稳定。
（4）因果、稳定。
（5）因果、稳定。
（6）因果、稳定。
（7）因果，但由于 。
（8） 在 时刻有值，故非因果。由于 的值都在 的时刻内，那么 ，故系统稳定。
1.17解：由图可知：
所以
（1）解：
（2）解：
通解
特解
带入方程得：
（3）解：
当 时，右边序列的围线C内包含 两个极点。故
因此
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。

数字信号处理第三版课后答案 第一章

数字信号处理第三版课后答案 第一章

数字信号处理第三版课后答案第一章数字信号处理第三版课后答案第一章第一章时域离散信号和时域离散系统练习和计算机问题解决1单位脉冲序列δ（n）及其加权和表示图1所示的序列。

题1图第一章时域离散信号和时域离散系统解决方案：x(n)=δ(n+4)+2δ(n+2)-δ(n+1)+2δ(n)+δ(n-1)+2δ(n-2)+4δ(n-3)+0.5δ(n-4)+2δ(n-6)2.给定信号：2n+5(x(n)=60-4≤n≤-10≤n≤4其它（1）绘制X（n）序列的波形，并标记每个序列的值；（2）用延迟单位脉冲序列及其加权和表示X（n）序列；第1章时域离散信号与时域离散系统(3)令x1(n)=2x(n-2),试画出x1(n)波形；(4)令x2(n)=2x(n+2),试画出x2(n)波形；（5）让X3（n）=x（2-n），尝试绘制X3（n）波形。

（1）x（n）序列的波形如问题2的图（I）所示。

(2)x(n)=-3δ(n+4)-δ(n+3)+δ(n+2)+3δ(n+1)+6δ(n)+6δ(n-1)+6δ(n-2)+6δ(n-3)+6δ(n-4)m4(2m5)(nm)6(nm)m0一4第一章时域离散信号和时域离散系统（3） X1（n）的波形是X（n）的波形，它向右移位2位，乘以2，然后绘制出图形如题2解图(二)所示。

(4)x2(n)的波形是x(n)的波形左移2位，再乘以2,画出该图如问题2的图（III）所示。

（5）绘制X3（n）时，首先绘制X（-n）的波形（即，将X（n）的波形绕纵轴旋转180°，然后向右移动2位。

X3（n）的波形如溶液2的图（IV）所示。

第1章时域离散信号与时域离散系统题2解图(一)第一章时域离散信号和时域离散系统问题2解决方案图（二）第1章时域离散信号与时域离散系统题2解图(三)第一章时域离散信号和时域离散系统问题2解决方案图（四）第1章时域离散信号与时域离散系统3.判断下面的序列是否是周期的;若是周期的，确定其周期。

数字信号处理-第1章习题答案

数字信号处理-第1章习题答案

解：
2 i 14i i 3 , N min 14 (1) N 0 3 / 7 3 (2) i 7, j 4, N min 56 2 j 2 j 14 j N2 0 / 7 2 i 8i N1 0 / 4 2 i
0
20
40
60 n
80
100
120
1 3 绘出如下序列的波形。 1.3
(1) x(n) 3 (n 3) 2 (n 1) 4 (n 1) 2 (n 2) (2) x(n) 0.5n R5 (n)
解 (1)
3
2
1
0 x(n n) -1 -2 2 -3 -4 -4
因此，T[.]为线性系统；
T x( n n1 ) nx ( n n1 ) T x( n n1 ) y ( n n1 ) y ( n n1 ) ( n n1 ) x ( n n1 )
因此 T[.]为时变系统。 因此， 为时变系统
1 16 确定下列系统的因果性与稳定性。 1.16
(2) 收敛区域为|z|>a，即圆|z|=a的外部。
1 0.8 0.6 0.4 Imagina ary Part 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1 -0.5 0 Real Part 0.5 1 1.5
j 1 1 2 e a c 1 2 a cos a 1 j (3) H (e ) j 2 e a d a 1 2a cos a
2 i
3 x(n) cos n 4 7
1 0.8 0.6 04 0.4 0.2 x(n) 0 -0.2 -0.4 -0 0.6 6 -0.8 -1

数字信号处理(第三版)第1章习题答案

－m≤3， 或写成n－3≤m≤n， 这样y(n)的非零区间要求m同时满足下
面两个不等式：
0≤m≤3
m－3≤m≤n
上面公式表明m的取值和n的取值有关， 需要将n作分段的假设。 按 照上式， 当n变化时， m应该按下式取值：
第九页，共105页。
max{0, n－3}≤m≤min{3, n}
当0≤n≤3时， 下限应该是0， 上限应该是n； 当4≤n≤6时， 下限应该是
y(n)=
n 1 y(n) 7 n
0
0≤n≤3
4≤n≤6
其它
第十一页，共105页。
在封闭式求解过程中， 有时候决定求和的上下限有些麻烦， 可借助于 非零值区间的示意图确定求和限。 在该例题中， 非零值区间的示意图如图
1.2.1所示。 在图1.2.1(b)中， 当n<0时， 图形向左移动， 图形不可能 和图1.2.1(a)的图形有重叠部分， 因此y(n)=0。 当图形向右移动时， 0≤n≤3， 图形如图1.2.1(c)所示， 对照图1.2.1(a)， 重叠部分的上下限自 然是0≤m≤n。 当图形再向右移动时， 4≤n≤6， 如图1.2.1(d)所示， 重 叠部分的上下限是n－3≤m≤3。 当图形再向右移动时, 7≤n， 图形不可能和
(1) x(n) Acos 3 πn A是常数
第二十二页，共105页。
图1.3.2
第二十三页，共105页。
［例1.3.5］已知x1(n)=δ(n)+3δ(n－1)+2δ(n－2)，x2(n)=u(n)－u(n－3)，
试求信号x(n)， 它满足x(n)=x1(n)*x2(n), 并画出x(n)的波形。
解： 这是一个简单的计算线性卷积的题目。
x(n)=x1(n)*x2(n) =［δ(n)+3δ(n－1)+2δ(n－2)］*［u(n)－u(n－3)

数字信号处理(吴镇扬)第一章习题解答

（2）解：
所求序列为双边序列，采用留数法求解。
当n>=1时，围线C内只有一个极点 ，
则：
当n<1时，围线外只有一个极点 ，利用辅助留数定理，则：
因此
（4）解：
1.12
(1)解：直接法
帕氏定理：
（2）解：直接法
帕氏定理：
（3）解：直接法
帕氏定理：
1.13
(1)解：
该系统不是线性系统；
该系统是时不变系统。
所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.Байду номын сангаас9
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
（2）解：
该系统不是线性系统；
该系统是时不变系统。
（3）解：
令 ，则
而
该系统是线性系统时不变系统。
注：
令 ，则
而
该系统是线性时不变系统。
（4）解：
该系统是线性系统时不变系统。
（5）解：
该系统是线性系统时变系统。
1.14解：
(1)
(2)
(3)
1.16
（1）解：因果、稳定。
(2)当n0<0时，系统非因果,不稳定。
(3) 当n0＞0时，该系统是因果系统；当n0＜0时，该系统是非因果系统；系统稳定。
（4）因果、稳定。
（5）因果、稳定。

数字信号处理方勇第一章习题答案

习 题1-1 有一个连续信号)2cos()(ψπ+=ft t x a ，式中Hz f 20=，2πψ=，（１） 求出)(t x a 的周期；（２） 用采样间隔s T 02.0=对)(t x a 进行采样，写出采样信号)(ˆt xa 的表达式； （３） 画出对应)(ˆt xa 的时域离散信号（序列）)(n x 的波形，并求出)(n x 的周期。

解：（1）)(t x a 的周期是s fT a 05.01==（2）∑∞-∞=-+=n a nT t fnT t x)()2cos()(ˆδψπ∑∞-∞=-+=n nT t nT )()40cos(δψπ（3）)(n x 的数字频率为πω8.0=，252=ωπ周期5=N 。

)28.0cos()(ππ+=n n x ，画出其波形如题1-1图所示。

题1-1图 1-2 设)sin()(t t x a π=，()()sin()a s s x n x nT nT π==，其中s T 为采样周期。

（1）)(t x a 信号的模拟频率Ω为多少？ （2）Ω和ω的关系是什么？（3）当s T s 5.0=时，)(n x 的数字频率ω为多少？ 解：（1）)(t x a 的模拟频率s rad /π=Ω。

（2）Ω和ω的关系是：s T ⋅Ω=ω。

（3）当s T s 5.0=时，rad πω5.0=。

1-3 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）)873cos()(ππ-=n A n x ，A 为常数；（2）)81()(π-=n j e n x 。

解： （1）πω73=，3142=ωπ，这是有理数，因此是周期序列，周期是14=T ； （2）81=ω，πωπ162=，这是无理数，因此是非周期序列。

1-4 研究一个线性时不变系统，其单位脉冲响应为指数序列)()(n u a n h n =，10<<a 。

对于矩阵输入序列，1,01()0N n N R n ≤≤-⎧=⎨⎩,其他 求出输出序列，并用MATLAB 计算，比较其结果。

数字信号处理教程习题分析与解答(程佩青)第一章

第一章 离散时间信号与系统1 .直接计算下面两个序列的卷积和)n (h *)n (x )n (y =请用公式表示。

分析：①注意卷积和公式中求和式中是哑变量m （ n 看作参量）， 结果)(n y 中变量是 n ,; )()()()()(∑∑∞-∞=∞-∞=-=-=m m m n x m h m n h m x n y ②分为四步 （1）翻褶（ -m ），（2）移位（ n ）,（3）相乘，; )( )( 4n y n n y n 值的，如此可求得所有值的）相加，求得一个（③ 围的不同的不同时间段上求和范一定要注意某些题中在 n如此题所示，因而要分段求解。

2 .已知线性移不变系统的输入为)n (x ,系统的单位抽样响应 为)n (h ,试求系统的输出)n (y ,并画图。

)(5.0)(,)1(2 )()4()(5.0)(,)2( )()3()()(,)( )()2()()(,)( )()1(3435n u n h n u n x n R n h n n x n R n h n R n x n R n h n n x n n n =--==-=====δδ分析：①如果是因果序列)(n y 可表示成)(n y ={)0(y ，)1(y ，)2(y ……}，例如小题（2）为)(n y ={1，2，3，3，2，1} ;②)()(*)( , )()(*)(m n x n x m n n x n x n -=-=δδ ;0 00 , 01()0 , ,()0,n n n a n N h n n n n x n n n β-⎧≤≤-=⎨⎩⎧≤⎪=⎨<⎪⎩其他()∑∑∑+-=+-=--+===-=-+≥nN n m mn n nN n m mn n m nn m m n h m x n y N n n 111N -00)()()( , 1)3(αββααβ全重叠时当()()()()βααβαβαβαββααβαβαβ==≠--=--=---+++--,)(,100111n n N N n N n n N n n n N n y③卷积和求解时，n 的分段处理。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

e j (0 n ) e j (0 n ) u ( n) ， 0 r 1 2
1-4
第一章
数字信号处理基本概念
我们将其分解为标准的指数序列形式，然后根据 Z 变换的求和定义式求得其对应的 Z 变换、收敛域并画出零极点图。 其 Z 变换为
1
X ( z ) Ar n cos(0 n ) z n A r n
收敛区域为 z r ，极点为 z re
j0
， re
j 0
，零点为 z 0 ， r cos( 0 ) cos 。
其对应的零极点图如题 1-6 图所示。 利用 MATLAB 画出其零极点,如题 1-6 图(b)所示： A=1; r=1; w0=4*pi; w=2*pi; x=2*r*cos(w0); y=A*r*cos(w0-w); b=[A*cos(w) -y ]; a=[1 -x r*r]; zplane(b,a);
k 0
N 1
an
1 aN 1 a 1
(
1 a n n N 1 )a 1 a
所以
0 , n0 1 a n 1 y ( n) , 0 n N 1 1 a n N 1 1 a n ( ) , N 1 n a 1 a
n 0 n
e j (0 n ) e j (0 n ) n z 2
A cos Arz 1 cos(0 ) A j 1 A j 1 e e 2 (1 re j0 z 1 ) 2 (1 re j0 z 1 ) 1 2rz 1 cos 0 r 2 z 2
1-4 研究一个线性时不变系统，其单位脉冲响应为指数序列 h( n) a n u ( n) ， 0 a 1 。 对于矩阵输入序列，
1 , 0 n N 1 RN (n) ,其他 0
求出输出序列，并用 MATLAB 计算，比较其结果。 分析：输入 x ( n) R N ( n) ，线性时不变系统的输出等于输入序列与单位脉冲响应的卷 积，用公式表示为 y ( n) x ( n) h( n)
3 7

8
) ， A 为常数；
1-1
第一章
1 j ( n ) 8 。
数字信号处理基本概念
（2） x ( n) e 解： （1）
2 14 3 ， ，这是有理数，因此是周期序列，周期是 T 14 ； 7 3 1 2 16 ，这是无理数，因此是非周期序列。 （2） ， 8
k
x ( k ) h( n k )

为了计算输出序列的第 n 个值，必须计算出乘积 x(k ) h(n k ) ，并将所得到的序列值 相加。 解：输出序列 y ( n) x ( n) h( n) （１） （２）

k
x(k ) h(n k ) 可以分成三种情况来求解：
1-2
第一章
数字信号处理基本概念
利用 MATLAB 求其响应,程序如下： a=1/2; N=20; n=0:N-1; c=[1]; d=[1 -a]; x=ones(1,N); y=filter(c,d,x); stem(n,y); ylabel('y(n)');
题 1-4 图 输出相应序列 y ( n) 1-5 设 x ( n) a n u ( n) ， h( n) b n u ( n) ab n 1u ( n 1) ，求 y (n) x(n) h(n) 。 解：
当 n 0 时，由于 h(n k ) 和 x ( k ) 的非零取样互不重叠，因此 y ( n) 0 。 当 0 n N 1 时，从 k 0 到 k n ， h(n k ) 和 x ( k ) 的非零取样值有重叠， 因此
y ( n)
k
x ( k ) h( n k ) a n k
题 1-6 图(b) 零极点图 讨论 通常将正弦序列信号展开为两个基本复指数序列和或差的形式，然后按照 Z 变 换定义式求起对应的 Z 变换和收敛域。对于 Z 变换表达式可表示为等比级数和的形式 的序列，其 Z 变换的收敛域是保证等比小于 1，如本例中要保证 q z re
1 j0
1 ，可
2n n ( 3)
n0 n0
m0
（2） y (n) nx(n) 是否为时不变系统，并利用 MATLAB x ( m) ，
n
1-6
第一章
数字信号处理基本概念
验证。 解： （1）令输入为 x(n n0 ) ，输出为 Y ( n) T [ x( n n0 )]
n n0 m0
n 0
n

an z n
1 an z n 1 1 az n 1

1 1 1 z (1 a 2 ) n n a z 1 1 1 az 1 n 0 1 az 1 1 az (1 az )( z a )
x(n) a ， 0 a 1 是一个双边序列，其收敛域为 a z 1 a 表示极点，极点为
m0
x(m n )
0
n
而 y ( n n0 )
x(m) Y (n) ，所以系统是时变的。
MATLAB 验证： 令 x( n) ( n 1) 2 ( n) ( n 1) ， n0 1 程序如下： x=[1 2 1];n0=1;n=-1:1; x0=[2 1];%x0为x横坐标非负的值 y=cumsum(x0); Y=cumsum(x); subplot(3,2,1);stem(n,x); xlabel('n');ylabel('x(n)');title('输入');axis([-1,3,0,4]); subplot(3,2,2);n=0:1;stem(n,y); xlabel('n');ylabel('y(n)');title('输出');axis([-1,3,0,4]); subplot(3,2,3);n=0:2;stem(n,x); xlabel('n');ylabel('x(n-n0)');title('输入');axis([-1,3,0,4]); subplot(3,2,5);n=0:2;stem(n,Y); xlabel('n');ylabel('Y(n)');title('输出');axis([-1,3,0,4]); subplot(3,2,4);n=1:2;stem(n,y); xlabel('n');ylabel('y(n-n0)');title('输出');axis([-1,3,0,4]);
5 z 1 , 2 z 3 的逆 Z 变换，并用 MATLAB 求解。 1 z 1 6 z 2
X ( z) 1 1 , 1 1 2z 1 3 z 1
解：由部分分式展开可得
因为 2 z 3 。所以得 x ( n ) MATLAB 求解： 程序如下： syms k z; Fz=5*z/(z^2+z-6); fk=iztrans(Fz,k) 运行结果： fk =2^k - (-3)^k 1-9 判断系统（1） y (n)
（１）双边指数序列 x(n) a
n
， 0 a 1；
（２）正弦调制序列 x(n) Ar n cos( 0 n )u (n) ， 0 r 1 。 解： （1）双边指数序列可写为
a n x ( n) n a
其 Z 变换为
1
,n 0 ,n 0
X ( z) an z n
周期 N 5 。


5 2
题 1-1 图
x(n) cos(0.8n 2) ，画出其波形如题 1-1 图所示。
1-2 设 x a (t ) sin(t ) ， x( n) xa ( nTs ) sin( nTs ) ，其中 Ts 为采样周期。 （1） x a (t ) 信号的模拟频率 为多少？ （2） 和 的关系是什么？ （3）当 Ts 0.5s 时， x ( n) 的数字频率 为多少？ 解： （1） x a (t ) 的模拟频率 rad / s 。 （2） 和 的关系是： Ts 。 （3）当 Ts 0.5s 时， 0.5rad 。 1-3 判断下面的序列是否是周期的，若是周期的，确定其周期。 （1） x(n) A cos( n
解： （1） x a (t ) 的周期是
Ta

1 0.05s f
ˆ a (t ) （2） x
n

cos(2fnT ) (t nT )

n
cos(40nT ) (t nT )
2
（3） x ( n) 的数字频率为
0.8 ，
X ( z)
所以， 其 Z 反变换为
z ，z a za z a za H ( z) ，z b z b z b z b z Y ( z) X ( z) H ( z) ， z b z b
y ( n) x ( n) h( n) 1[Y ( z )] b n u ( n)
显然，在 z a 处， X ( z ) 的极点被 H ( z ) 的零点所抵消，如果 b a ，则 Y ( z ) 的收敛域 比 X ( z ) 与 H ( z ) 收敛域的重叠部分要大。 1-6 求下列序列的 Z 变换及其收敛域，并用 MATLAB 画出零极点示意图。
1-3
第一章
数字信号处理基本概念