3-1&2 LKJ2000型监控装置系统组成及工作原理

第三章习题解答3-1 某圆柱形固定床填充的催化剂直径为p d ，高为h ，试求等体积的当量直径及球形度。

解：h d d e 2p 346ππ=，32p 23h d d e = ()p 312p p 2322218)24(23d h h d h d d h d P P +=⋅⋅+⨯⎪⎭⎫ ⎝⎛=πππφ3-2 求20mm×20mm×25mm 的长方体颗粒的体积当量直径，表面积当量直径，比表面积当量直径及形状系数。

解：体积当量直径：mm V d ev 7.262520206633=⨯⨯⨯==ππ表面积当量直径：mm Sd es 8.282)252020202020(=⨯⨯+⨯+⨯==ππ比表面积当量直径：mm S V a d ea 1.232)252020202020(252020666=⨯⨯+⨯+⨯⨯⨯⨯=== 形状系数：86.08.287.26222222=====es ev es ev P s d d d d S S ππφ 3-3 由边长皆为2mm 的立方体，直径和高度均为2mm 的圆柱体及直径为3mm 的球体各10kg 组成的均匀颗粒床层，床层直径为0.2m ，高度为 1 m 。

已知颗粒的密度皆为1900kg/m 3，求床层的空隙率和颗粒的平均比表面积。

解： 床层体积：3220314.012.044m h d V b =⨯⨯==ππ颗粒体积：30158.01900310m V P =⨯= 床层空隙率：497.00314.00158.00314.0=-=-=bpb V V V ε 颗粒的平均比表面积：3球柱立a a a a ++=-13000002.0002.0002.06002.0002.0-=⨯⨯⨯⨯=m a 立 1223000002.0)002.0(4002.02)002.0(4-=⨯⨯⋅+⨯⨯=m a πππ柱 1322000003.066003.0003.0-==⨯⨯=m a ππ球 11 2.67676232000300030003---==++=++=mm m a a a a 球柱立 3-4 某形状近似球形的微小固体颗粒，其沉降运动处于斯托克斯定理区，试计算（1）该颗粒在20℃与200℃的常压空气中的沉降速度之比为多少？（2）该颗粒在20℃与50℃的水中的沉降速度之比为多少？[（1）1.44，（2）0.55]解：（1）20℃空气的粘度s Pa ⋅⨯=-51081.1μ，200℃空气的粘度s Pa ⋅⨯=-5'106.2μ，因沉降速度处于斯托克斯定律区，ρρ>>p ，故()()()()44.11081.1106.2181855''''22'=⨯⨯=--=--=--μρρμρρμρρμρρs s s s t t g d gd u u （2）20℃水的粘度s Pa ⋅⨯=-3101μ，50℃水的粘度s Pa ⋅⨯=-3'1055.0μ，因沉降速度处于斯托克斯定律区，并考虑到液体的密度随温度变化很小，故()()()()55.01011055.0181833'''''22'=⨯⨯=≈--=--=--μμμρρμρρμρρμρρs s p p p p t t g d g d u u 无论是气体还是液体，温度的改变主要是通过粘度的变化而影响沉降速度。

正保远程教育旗下品牌网站 美国纽交所上市公司(NYSE:DL)自考365 中国权威专业的自考辅导网站官方网站： 高等教育自学考试辅导《护理学研究》第三章第一节讲义选择研究问题一、研究问题的概念指研究者想要回答的特殊疑问，它确定了研究中所需收集资料的类型，研究者一般是从较宽泛的领域中识别出问题。

研究目的是指研究者通过实施研究所要达到的特殊效果，是为了解决问题或通过汇集相关信息以促进问题的解决。

课题是指一个已确立的科研题目，科研项目由若干个研究课题组成，是较复杂和综合性较强的研究题目。

课题与项目两者之间的区别在于研究课题规模较小，周期较短，而科研项目则周期较长，复杂程度和规模较大。

二、研究问题的来源（选择）护理领域需要研究的问题和尚待验证的理论很多，研究课题主要来自理论、实践、文献或他人建议。

一个研究问题的产生，常需经过较长期的观察和思考，主要从护理实践和日常工作中发现问题，逐步形成新的想法，从而提出研究课题。

选题是一个严密的科学思维过程，也是科技工作者理论水平和科研能力的综合体现。

所以研究问题的产生需要有背景，需要有科学理论依据和实践基础，如在日常护理工作中遇到一些不能解释的现象或无法解决的问题，可在相关理论和实践经验的指导下，逐渐形成解决问题的具体设想和方法，从而提出要研究的课题。

1.研究者自选题来源 选题过程是研究工作的重要阶段，如何发现和选择研究问题常是护理工作者的难点。

研究问题通常来自护士的临床实践、阅读护理文献、社会问题及已有的护理理论等。

不少人平时遇到的问题很多，但开始要做研究工作时，却又想不起来或感到很笼统。

选择一个好的研究问题的确不是容易的事，需要平时多观察、多看文献和思考。

目前护理研究问题大多为个人自选，由国家下达的研究题目还不多。

研究题目的方向常见有：①研究各临床护理专业问题。

②比较两种或两种以上的护理措施的效果。

③评价新的护理方法或护理模式。

④护理教育。

⑤护理管理。

⑥发展和检验测量工具等。

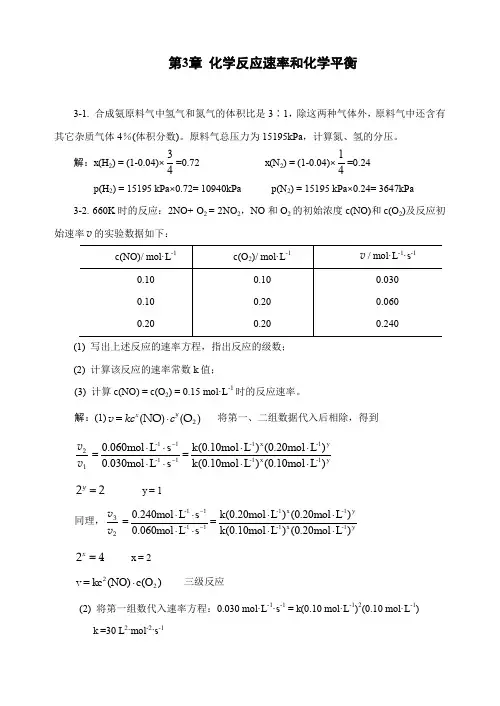
3 地基应力和沉降典型范例【例3-1】有一矩形基础放置在均质粘性土层上,如图所示。

基础长度l=10m，宽度b=5m，埋置深度d=1.5m，其上作用着中心荷载P=10000kN。

地基土的天然湿重度为20kN/m3，土的压缩曲线如图所示。

若地下水位距基底2.5m，试求基础中心点的沉降量。

【解题思路】本例题是典型的利用现有地基沉降量计算规范法计算建筑物地基沉降的算例，在计算中主要把握好规范法计算各个步骤，计算公式应用正确。

具体步骤可以见教材说明。

【解答】（1）基底附加压力由l/b=10/5=2<10可知，属于空间问题，且为中心荷载，所以基底压力为基底净压力为（2）对地基分层因为是均质土，且地下水位在基底以下2.5m处，取分层厚度H i=2.5m。

（3）各分界层面的自重应力计算（注意：从地面算起）根据分界层面上自重应力，绘制自重应力分布曲线，如图所示。

（4）各分界层面的附加应力计算该基础为矩形，属空间问题，故应用“角点法”求解。

为此，通过中心点将基底划分为4块相等的计算面积，每块的长度l1=5m，宽度b1=2.5m。

中心点正好在4块计算面积的公共角点上，该点下任意深度z i处的附加应力为任一分块在该处引起的附加应力的4倍，计算结果如下表所示。

附加应力计算成果表 位 置 z i z i/b l/b Kc0 0 0 2 0.2500 170 1 2.5 1.0 2 0.1999 136 2 5.0 2.0 2 0.1202 82 3 7.5 3.0 2 0.0732 50 4 10.0 4.0 2 0.047432 512.55.020.032822根据分界层面上附加应力，绘制附加应力分布曲线，如图所示。

（5）确定压缩层厚度从计算结果可知，在第4点处有 ，所以，取压缩层厚度为10m 。

（6）计算各分层的平均自重应力和平均附加应力 （7）初始孔隙比和压缩稳定后的孔隙比层 次平均自重应力 （kPa ） 平均附加应力 （kPa ） 加荷后总的应力（kPa ） 初始孔隙比压缩稳定后的孔隙比Ⅰ 55 153 208 0.935 0.870 Ⅱ 94 109 203 0.915 0.870 Ⅲ 122 66 188 0.895 0.875 Ⅳ 150 41 191 0.885 0.873（8）计算地基的沉降量分别计算各分层的沉降量，然后累加即地基最终沉降量【例3-2】柱荷载F=1190kN，基础埋深d=1.5m，基础底面尺寸l×b＝4m×2m；地基土层如图所示，试用《地基规范》方法计算该基础的最终沉降量。

习题解答3-1．填空题（1） 在模拟通信系统中，有效性与已调信号带宽的定性关系是（ 已调信号带宽越小，有效性越好），可靠性与解调器输出信噪比的定性关系是（解调器输出信噪比越大，可靠性越好）。

（2） 鉴频器输出噪声的功率谱密度与频率的定性关系是（功率谱密度与频率的平方成正比），采用预加重和去加重技术的目的是（提高解调器输出信噪比）。

（3） 在AM 、DSB 、SSB 、FM 等4个通信系统中，可靠性最好的是（FM ），有效性最好的是（SSB ），有效性相同的是（AM 和DSB ），可靠性相同的是（DSB 、SSB ）。

（4） 在VSB 系统中，无失真传输信息的两个条件是：（相干解调）、（系统的频率特性在载频两边互补对称）。

（5） 某调频信号的时域表达式为6310cos(2105sin10)t t ，此信号的载频是（106）Hz ，最大频偏是（2500）Hz ，信号带宽是（6000）Hz ，当调频灵敏度为5kHz/V 时，基带信号的时域表达式为（30.5cos10t ）。

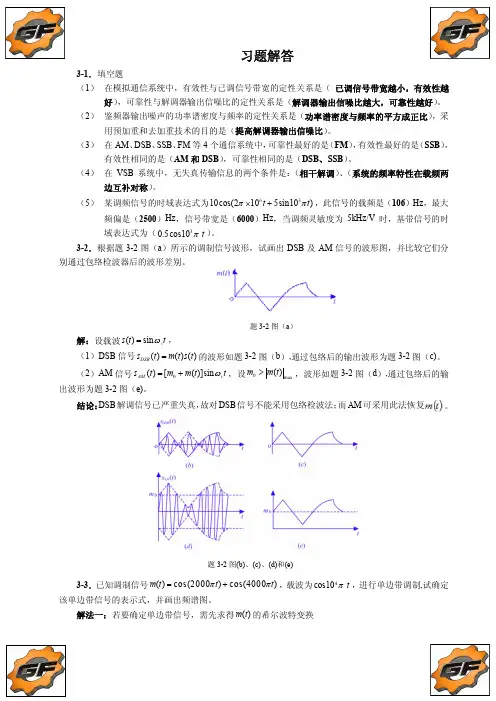
3-2．根据题3-2图（a ）所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别通过包络检波器后的波形差别。

解：设载波()sin c s t t ，（1）DSB 信号()()()DSB s t m t s t 的波形如题3-2图（b ）,通过包络后的输出波形为题3-2图（c)。

（2）AM 信号0()[()]sin AM c s t m m t t ，设0max ()m m t ，波形如题3-2图（d ）,通过包络后的输出波形为题3-2图（e)。

结论：DSB 解调信号已严重失真，故对DSB 信号不能采用包络检波法；而AM 可采用此法恢复。

3-3．已知调制信号()cos(2000)cos(4000)m t t t ，载波为4cos10t ，进行单边带调制,试确定该单边带信号的表示式，并画出频谱图。

解法一：若要确定单边带信号，需先求得()m t 的希尔波特变换题3-2图（a ）题3-2图(b)、(c)、(d)和(e)ˆ()cos(2000)cos(4000)22sin(2000)sin(4000)mt t t t t故上边带信号11ˆ()()cos ()sin 2211cos(12000)cos(14000)22USB c c s t m t t mt t t t下边带信号为11ˆ()()cos ()sin 2211cos(8000)cos(6000)22LSB c c s t m t t mt t t t其频谱图如题2-3图所示。

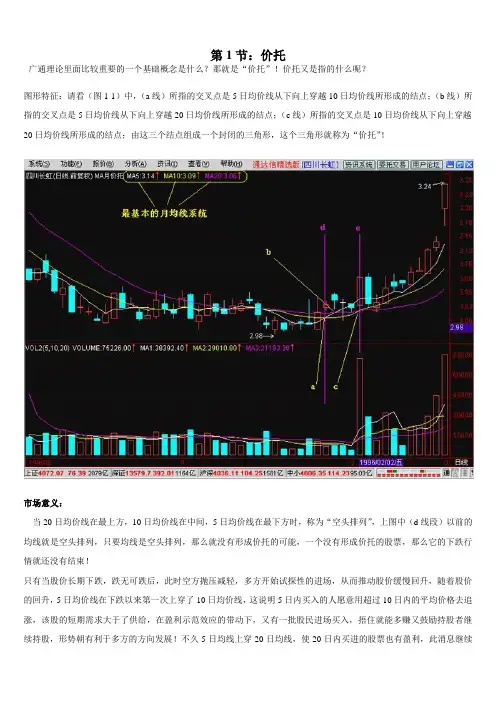
第1节：价托广通理论里面比较重要的一个基础概念是什么？那就是“价托”！价托又是指的什么呢？图形特征：请看（图1-1）中，（a线）所指的交叉点是5日均价线从下向上穿越10日均价线所形成的结点；（b线）所指的交叉点是5日均价线从下向上穿越20日均价线所形成的结点；（c线）所指的交叉点是10日均价线从下向上穿越20日均价线所形成的结点；由这三个结点组成一个封闭的三角形，这个三角形就称为“价托”！市场意义：当20日均价线在最上方，10日均价线在中间，5日均价线在最下方时，称为“空头排列”，上图中（d线段）以前的均线就是空头排列，只要均线是空头排列，那么就没有形成价托的可能，一个没有形成价托的股票，那么它的下跌行情就还没有结束！只有当股价长期下跌，跌无可跌后，此时空方抛压减轻，多方开始试探性的进场，从而推动股价缓慢回升，随着股价的回升，5日均价线在下跌以来第一次上穿了10日均价线，这说明5日内买入的人愿意用超过10日内的平均价格去追涨，该股的短期需求大于了供给，在盈利示范效应的带动下，又有一批股民进场买入，捂住就能多赚又鼓励持股者继续持股，形势朝有利于多方的方向发展！不久5日均线上穿20日均线，使20日内买进的股票也有盈利，此消息继续鼓动人们买进该股，鼓励持股者继续持股，该股的需求量急增，而供给量却越来越小，终于有一天，10日均线上穿了20日均线，最终三条均线封闭成一个三角形托，这使盈利的人扩展到5日持股者、10日持股者、20日持股者，这种循环继续强化的话，三条均线将向上形成多头排列上图中（e线段）以后的均线就是多头排列，从而展开一轮多头行情！三角形“托”在底部形态中是否有普遍性，考证后发现绝大多数个股都有这个规律，而在长期下跌的末端，这种三角形托几乎成了底部的代名词。

价托的分类：价托按照周期长短和不同场合的组合使用等分为以下几种。

1：月价托（由5日、10日、20日均价线组成），该组合较为敏感，对中长期底部的提示作用较弱，对阶段性短期底部的提示有一定的参考作用；见（图1-2）2：季价托（由20日、40日、60日均价线组成），该组合的稳定度较好，对中长期底部的提示作用较好，但对阶段性短期底部的提示作用稍显迟钝；3：短长结合的价托（由5日、10日、60日均价线组成），该组合既有一定的稳定度，也有一定的灵敏度4：超短期均线价托（由5、10、20单位均线组合而成），一般是指用在15分钟、30分钟、60分钟等K线周期上的均线系统，该系统一般用来对被怀疑的股价底部区间进行微观分析，以指导对个股进行精确的瞄准；注：说到精确制导好像有点跑题了，那是中、高级班要解决的问题，必须结合广通多项单一技术进行综合的研判，比如结合“扇骨线”技术、“内径线”技术、“2+3均线系统”、“多周期综合分析”等等内容一同研判，那才能做到短线精确制导，现在我们新生要解决的问题主要是基础概念的问题，一部份新同学恐怕连多方炮的正确含意都没真正的搞懂吧？所以大家要有虚心、耐心、恒心，只要认真做完每一课作业，相信你们对于这些最基础的理论能够掌握得更好一些！第2节：量托在讨论日K线5日、10日和20日均价线的同时，我们必需同时研究5日、10日和20日均量线，在某种意义上说，均量线的三角形托甚至比均价线的三角形托更加重要。

习题3-1.选择题：（1）已知单位负反馈闭环系统是稳定的，其开环传递函数为：)1(2)s )(2+++=s s s s G （，系统对单位斜坡的稳态误差是： 3-2 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解 Φ()()./(.)s L k t s ==+001251253-3 一阶系统结构图如图3-45所示。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。

图 题3-3图解 由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K sK K s K s 令闭环增益212==ΦK K ， 得：5.02=K 令调节时间4.03321≤==K K T t s ，得：151≥K 。

3-4 设二阶控制系统的单位阶跃响应曲线如图 所示。

如果该系统为单位反馈控制系统，试确定其开环传递函数。

图 题3-4图 解：由图知，开环传递函数为3-5 设角速度指示随动统结构图如图3-40所示。

若要求系统单位阶跃响应无超调，且调节时间尽可能短，问开环增益K 应取何值，调节时间s t 是多少图3-40 题3-5图解：依题意应取 1=ξ，这时可设闭环极点为02,11T -=λ。

写出系统闭环传递函数Ks s Ks 101010)(2++=Φ闭环特征多项式20022021211010)(⎪⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛+=++=T s T s T s K s s s D 比较系数有 ⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛=K T T 101102200 联立求解得 ⎩⎨⎧==5.22.00K T 因此有 159.075.40''<''==T t s3-6 图所示为某控制系统结构图，是选择参数K 1和K 2，使系统的ωn =6，ξ=1.3-7 已知系统的特征方程，试判别系统的稳定性，并确定在右半s 平面根的个数及纯虚根。

三阶系统.doc这时，调节时间s t 近似为： ns t ωξξ)1(42--=(3-13)图3-3 二阶系统模拟电路K K K K R100,40,20,10=图3-3是图3-1的模拟电路图。

表3-1列出有关二阶系统在三种情况（欠阻尼、 临界阻尼、过阻尼）下具体参数的表达式，以便计算理论值。

表3-12、图3-4是典型三阶系统原理方框图图2-4 典型三阶系统t )开环传递函数为：)1)(1()1)(1()()(2121021++=++=S T S T S KS T S T S T K K S H S G (3-14)其中，021K K K= (开环增益)图3-5是典型三阶系统模拟电路图。

op1op2op3op5r(t)200k200k200k500k2μ1μ100k 1μ500k10k10kC(t)图2-5 三阶系统模拟电路100k R-----op6三阶系统模拟电路的开环传递函数为：)1)(1()15.0)(11.0(500)()(21++=++=S T S T S KS S S R S H S G (3-15)式中R 的单位为K Ω，比较式(1-14)和(2-15)得⎪⎪⎩⎪⎪⎨⎧====RK T T T 5005.01.01210 (3-16) 系统的特征方程为0)()(1=+S H S G ，由式(2-14)可得0)1)(1(21=+++K S T S T S展开得到：0)(221321=++++K S S T T S T T (3-17)将式(2-16)代入式(2-17)得到06.005.023=+++K S S S或020201223=+++K S S S (3-18)用劳斯判据求出系统稳定、临界稳定和不稳定时的开环增益 3S 1 202S 12 20K图图1S12202012K-⨯ 00S 20K由0202012>-⨯K020>K得到系统稳定范围： 120<<K由0202012=-⨯K得到系统临界稳定时： 12=K 由0202012<-⨯K得到系统不稳定范围 12>K将R K500= 代入上式得到：Ω>K R 7.41 系统稳定Ω=K R 7.41 系统临界稳定 Ω<K R 7.41 系统不稳定系统稳定、临界稳定和不稳定时输出波形如图3-6A,3-6B,3-6C 所示。

第三章思考题1. 试说明集总参数法的物理概念及数学处理的特点答：当内外热阻之比趋于零时，影响换热的主要环节是在边界上的换热能力。

而内部由于热阻很小而温度趋于均匀，以至于不需要关心温度在空间的分布，温度只是时间的函数， 数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。

2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答：要改善热电偶的温度响应特性，即最大限度降低热电偶的时间常数,形状上要降低体面比，要选择热容小的材料，要强化热电偶表面的对流换热。

3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题 答；所谓“无限大”平板，是指其长宽尺度远大于其厚度，从边缘交换的热量可以忽略 不计，当平板两侧换热均匀时，热量只垂直于板面方向流动。

如薄板两侧均匀加热或冷却、 炉墙或冷库的保温层导热等情况可以按无限大平板处理。

4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答：非稳态导热过程进行到一定程度,初始温度分布的影响就会消失，虽然各点温度仍 随时间变化,但过余温度的比值已与时间无关，只是几何位置()和边界条件(Bi 数) 的函数，亦即无量纲温度分布不变，这一阶段称为正规状况阶段或充分发展阶段。

这一阶段的数学处理十分便利，温度分布计算只需取无穷级数的首项进行计算。

5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是： 这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。

你是否同意这种看法,说明你的理由。

答：我不同意这种看法，因为随着时间的推移，虽然物体中各点过余温度的比值不变 但各点温度的绝对值在无限接近。

这与物体中各点温度趋近流体温度的事实并不矛盾。

6. 试说明Bi 数的物理意义。