夫琅禾费单缝衍射次极大位置
- 格式：ppt
- 大小：1.07 MB
- 文档页数：47
下载文档原格式
合集下载
夫琅禾费衍射实验报告
dsinu??在单缝衍射因子具有极大值的地方即在???0的地方duu??除了在u???0处出现衍射主极强外还在一系列位置上出现衍射的次极强
[实验题目]
夫琅禾费衍射的定量研究
[实验目的]
1、掌握在光学平台上组装、调整光路的基本方法； 2、观察并定量测定不同衍射元件产生的光衍射图样； 3、学习微机自动控制和测量衍射光强的分布及其相关参量。
[实验内容]
1、掌握在光学平台上组装、调试产生夫琅禾费衍射的光路； 2、 定量研究单缝衍射图样分布规律 （光强比、 对称性、 缝宽等） ， 统一取第二排第四列的单狭缝（缝.宽 b=175μm） ； 3、定量研究三缝衍射光强分布，计算缝间距和缝宽(缝宽 b=40 μm,缝间距 d=90μm)，定性分析干涉和衍射的相互关系； 4、定性观察 10 个不同衍射屏衍射的光强分布。
2
2
表示衍射光场任意方向的相对光强。
单缝衍射光强分布的特点： 单缝的夫琅禾费衍射图样的中心有一 个主极强(零级衍射斑)，两侧都有一系列次极强和暗斑。主极强出现 在 sin
0 的地方， 原因是到这里的各条衍射光线有相同的
相位，它们相干叠加的结果具有最大的光强。 几何光学中的光线就是零级衍射线， 几何光学中的象点就是零级 衍射斑的中心。 在单缝衍射因子具有极大值的地方， 即在
一、单缝衍射 计算光强比： 背景光： I p
I 3 I 4 4 15 9.5 2 2
I1 I 2 175 172 1.83%( 10%) . 对称性要求： I I 172 175 1 2 Ip 9.5 2 2
4
主极强位置与缝数目 N 无关，但 N 越大，主极强宽度越小；相 邻主极强之间有 N-1 个暗纹和 N-2 个次极强；光强分布的外部轮廓 （包络线型）与单缝衍射的形状相同，这是单缝衍射因子的作用。
[实验题目]
夫琅禾费衍射的定量研究
[实验目的]
1、掌握在光学平台上组装、调整光路的基本方法； 2、观察并定量测定不同衍射元件产生的光衍射图样； 3、学习微机自动控制和测量衍射光强的分布及其相关参量。
[实验内容]
1、掌握在光学平台上组装、调试产生夫琅禾费衍射的光路； 2、 定量研究单缝衍射图样分布规律 （光强比、 对称性、 缝宽等） ， 统一取第二排第四列的单狭缝（缝.宽 b=175μm） ； 3、定量研究三缝衍射光强分布，计算缝间距和缝宽(缝宽 b=40 μm,缝间距 d=90μm)，定性分析干涉和衍射的相互关系； 4、定性观察 10 个不同衍射屏衍射的光强分布。
2
2
表示衍射光场任意方向的相对光强。
单缝衍射光强分布的特点： 单缝的夫琅禾费衍射图样的中心有一 个主极强(零级衍射斑)，两侧都有一系列次极强和暗斑。主极强出现 在 sin
0 的地方， 原因是到这里的各条衍射光线有相同的
相位，它们相干叠加的结果具有最大的光强。 几何光学中的光线就是零级衍射线， 几何光学中的象点就是零级 衍射斑的中心。 在单缝衍射因子具有极大值的地方， 即在
一、单缝衍射 计算光强比： 背景光： I p
I 3 I 4 4 15 9.5 2 2
I1 I 2 175 172 1.83%( 10%) . 对称性要求： I I 172 175 1 2 Ip 9.5 2 2
4
主极强位置与缝数目 N 无关，但 N 越大，主极强宽度越小；相 邻主极强之间有 N-1 个暗纹和 N-2 个次极强；光强分布的外部轮廓 （包络线型）与单缝衍射的形状相同，这是单缝衍射因子的作用。
夫琅禾费单缝衍射光强分布的研究
夫琅禾费单缝衍射光强分布的研究（Research Of Fraunhofer Single Slot Diffraction Of LightIntensity Distribution）摘要：我们在光学中学习了有关夫琅禾费单缝衍射和圆孔衍射的内容，本文主要是对夫琅禾费单缝衍射光强的计算公式进行数学推导以及拓展，并且根据推导的数学公式对夫琅禾费单缝衍射光强分布情况进行讨论，对夫琅禾费单缝衍射的特点进行分析介绍。
关键词：夫琅禾费单缝衍射（Fraunhofer single slot diffraction）、光强（Light intensity）、光强分布（Light intensity distribution）、最大值（Maximum）引言：光的衍射是光的波动性的重要现象之一。
衍射现象即波在传播过程中不沿直线传播，而是向各方向绕射的现象。
而光绕过障碍物偏离直线传播而进入几何阴影，并在屏幕上出现光强分布不均匀的现象，称为光的衍射。
在衍射现象中，把平行光束的衍射现象，称为夫琅禾费衍射。
夫琅禾费衍射在光学研究中有着重要意义，它主要包括单缝衍射、圆孔衍射。
这里我重点介绍夫琅禾费单缝衍射的光强分布特点。
一、夫琅禾费单缝衍射实验装置与衍射图样的特点。
所谓夫琅禾费衍射是指光源、衍射屏和观察屏三者之间都是相距无限远的衍射情况。
即相当于入射光和衍射光都是平行的情况。
在这种情况下计算衍射花样中光强的分布时，数学运算就比较简单。
所谓光源在无限远，实际上就是把光源置于第一个透镜的焦平面上，使之成为平行光束；所谓观察角在无限远，实际上是在第二个透镜的焦平面上观察衍射花样。
由于透镜的会聚，衍射花样的光强将比菲涅耳衍射花样的光强大大增加。
夫琅禾费单缝衍射包含着衍射现象的许多主要特征。
夫琅禾费单缝衍射光路图如下图所示：夫琅禾费单缝衍射图样的主要特点如下：（1）中央有一条特别明亮的亮条纹，其宽度是其他亮条纹的两倍；其他亮条纹的宽度相等，亮度逐渐下降。
9单缝夫琅禾费衍射ok
测径
a
I缝 (P) I丝 (P) P 0
13
1
x2 x1 0
x
x 0
I
0
f
b. 其他明纹（次极大）宽度
asin a k
a
1 x f x0 a 2
—衍射明纹宽度的特征
零级亮斑的宽度比其余的大一倍
14
入射波长变化，衍射效应如何变化 ?
f 0
相邻窄带发的子波到p点的相位差为：
2
x sin
2 a sin N
P 点即为 N 同频率、同振幅、相差依次为△ 的子波的叠加
（矢量合成）
4
P 点的合振幅 Ep 就是各子波的振幅矢量和的模； 相邻矢量
间的夹角为各子波间振动的相位差
对于O点： 0， 0
单缝衍射因子
2. 菲涅耳—基尔霍夫衍射公式
i E ( p) r0
x
ikr E ( Q ) e d 0 0
傍轴条件
焦平面
x
r
a
r x 0 O r
P
P0
s
f
i ikr E ( p ) E (Q) e dxdy f
r r r0 x sin
2 a
0.047 0.017 0
a
2
a
a
sin
(5)条纹宽度
a.中央明纹宽度
2 a
1
x2 x1 0
x
x 0
I
0
角宽度
傍轴条件
f
a
I缝 (P) I丝 (P) P 0
13
1
x2 x1 0
x
x 0
I
0
f
b. 其他明纹（次极大）宽度
asin a k
a
1 x f x0 a 2
—衍射明纹宽度的特征
零级亮斑的宽度比其余的大一倍
14
入射波长变化，衍射效应如何变化 ?
f 0
相邻窄带发的子波到p点的相位差为：
2
x sin
2 a sin N
P 点即为 N 同频率、同振幅、相差依次为△ 的子波的叠加
（矢量合成）
4
P 点的合振幅 Ep 就是各子波的振幅矢量和的模； 相邻矢量
间的夹角为各子波间振动的相位差
对于O点： 0， 0
单缝衍射因子
2. 菲涅耳—基尔霍夫衍射公式
i E ( p) r0
x
ikr E ( Q ) e d 0 0
傍轴条件
焦平面
x
r
a
r x 0 O r
P
P0
s
f
i ikr E ( p ) E (Q) e dxdy f
r r r0 x sin
2 a
0.047 0.017 0
a
2
a
a
sin
(5)条纹宽度
a.中央明纹宽度
2 a
1
x2 x1 0
x
x 0
I
0
角宽度
傍轴条件
f
2—3 夫琅和费单缝衍射
3、狭缝上所有次波在P 的叠加
积分过程见（附录2－1） b sinu u sin A A A0 sincu 令 p 0 u
2 sin u 2 2 2 2 Ap A0 A sin c u 0 2 u
I p I 0 sinc 2 u P点光强随θ的分布
16
三、强度公式的讨论 1、最大最小位置：
y2 = u
-
·
-2.46
·
-1.43
· 0
0
+1.43
+2.46
解得 :
相应 :
u 1.43， 2.46， 3.47， „
b sin 1.43 , 2.46 , 3.47 ,„
19
前几个次最大的位置
次最大序号 次最大位置 相对强度
u
1.43 2.46
(k 1, 2, ) 暗纹 (k 1, 2, ) 明纹 中央明纹
•正、负号表示衍射条纹对称分布于中央明纹的两侧 •对于任意衍射角，单缝不能分成整数个半波带，
在屏幕上光强介于最明与最暗之间。
方法一、菲涅耳半波带法
I / I0
明纹宽度
中央明条纹的角宽度 为中央两侧第一暗条纹 之间的区域:
3.47
4.48
sin
3 2b 5 2.46 b 2b 7 3.47 b 2b 9 4.48 b 2b 1.43 b
I I 0
1 2 3 4
0.047
0.017
0.008
0.005
1 sin k0 k 2 b
b
0
sin (2k 1)
2b
光强的分布实验数据记录表格
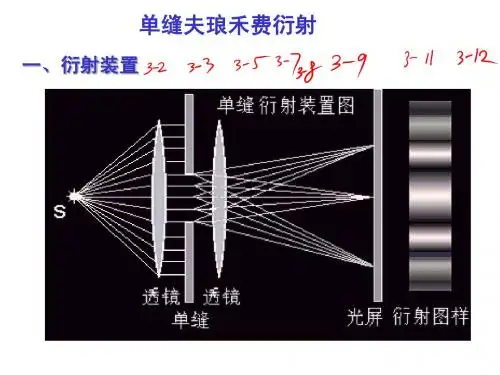
竭诚为您提供优质文档/双击可除光强的分布实验数据记录表格篇一：实验11光强分布实验11光强分布实验中切勿用眼对视激光否则会造成视网膜永久性损伤一、实验理论简介光的衍射是光的波动性的一种重要表现。
当光在传播过程中经过障碍物时，如不透明物体的边缘、小孔、细线、狭缝等，一部分光会传播到几何阴影中去，产生衍射现象。
如果障碍物的尺寸与波长相近，那么这样的衍射现象就比较容易观察到。
单缝衍射有两种，一种菲涅耳夫衍射——光源和衍射屏到衍射物的距离为有限远时的衍射，即所谓近场衍射，入射波和衍射波都是球面波；另一种为夫琅和费衍射——光源至单缝的距离和单缝到衍射屏的距离均为无限远（或相当于无限远），即要求照射到单缝上的放射光、衍射光都为平行光（激光满足要求），即所谓远场衍射，入射波和衍射波都可看做平面波。
本实验观察夫琅和费衍射。
实验中使用半导体激光作为光源，由于激光束的方向性好，所以可将激光看做平行光使用。
马吕斯定律：当两偏振片相对转动时，透射光强就随着两偏振片的透光轴的夹角而改变。
如果偏振片是理想的，当的它们的透光轴互相垂直时，投射光强应为零：当交角θ为其他值时，透射光强i为:i=i0cos2θ式中i0是两光轴平行（θ=0）时的透射光强。
上式称为马吕斯定律。
二、实验目的：1．观察夫琅和费单缝衍射现象，加深对光的波动性理解。
2．握用硅光电池作用原理测量单缝的衍射光强和偏振光的光强分布，验证马吕斯定律。
三、实验装置图11、激光电源2、半导体激光器3、扩束镜及平行光管4、二维调节架5、小孔狭缝板、光栅板、可调狭缝、小孔屏、起偏检偏装置6、光电探头7、一维光强测量装置8、数字式检流计四、实验原理p图2p0本实验仅研究夫琅和费单缝衍射。
平行光通过单缝在离单缝无限远处产生的衍射为夫琅和费衍射。
本实验采用激光光源，而且单缝离屏的间距d远大于缝宽a，所以产生平行光的透镜和观察衍射图样的透镜均可省略，如图2所示。
设中央亮纹的光强为i0，经计算得出屏幕上与光轴成角的p处的光强：ii0sin2uu2(uasin)(1)-3-2-023u图3当u=0(=0)时，即i=i0，为中央主极大。
夫琅禾费单缝衍射实验的教学研究
3.1“焦面接收”装置
把单色点光源 放在凸透镜 的前焦面上，经透镜 后的光束成为平行光垂直照在单缝 上，由惠更斯—菲涅耳原理，位于狭缝波阵面上每一点都可看成新的子波波源，它们向各个方向发射球面次波，这些次波经透镜 会聚于 的后焦面上，把接收屏 放在凸透镜 的后焦面上，则由几何光学可知 、 相当于距单缝 无限远。
2夫琅禾费衍射
由光源、衍射屏和接收屏组成的系统，按它们相互间距的大小，将衍射分为两大类。一类是光源和接收屏（或两者之一）距离衍射屏有限的为菲涅尔衍射；另一类是光源和接收屏都距离衍射屏为无限远的夫琅和费衍射[1]。
3实现夫琅和费单缝衍射的几种实验装置
要实现夫琅禾费衍射，必须保证光源到单缝的距离和单缝到衍射屏的距离均无限远（或相当于无限远），但是,把光源及接收屏放在离衍射屏无限远在实际上是做不到的。因此，必须采取相应的措施，才能实际形成夫琅禾费衍射。要使光源距狭缝无限远，实际上可以把光源置于第一个透镜的焦平面上，使之成为平行光束；要使观察屏距狭缝无限远，实际上可以再第二个透镜的焦平面上放置观察屏幕。下面介绍下面将介绍三种形成夫琅禾费衍射的装置[2]。
(a) (b)
图3 两种像面接收装置
Fig.3Two surface receivers
4夫琅禾费衍射图样规律
本实验采用的是如图2所示的远场接受装置,S是波长为 的单色光源，置于透镜 的前焦面上，单色光经透镜 后形成一束平行光投射于狭缝为 的单缝AB上。狭缝上各点可以看成是新的波源，由新的波源向各个方向发出球面次波。这些次波可以看成很多不同方向的平行光束。当衍射屏距离单缝的距离Z满足 ,由惠更斯—菲涅尔原理可推出衍射屏上任意一点 光强 的分布规律为[6]：
可以对L的取值范围进行估算：实验时，若取 ，入射光是 激光，其波长为632.80nm， ，所以只要取 ，就可满足夫琅和费衍射的远场条件。但实验证明，取 ，结果较为理想。
把单色点光源 放在凸透镜 的前焦面上，经透镜 后的光束成为平行光垂直照在单缝 上，由惠更斯—菲涅耳原理，位于狭缝波阵面上每一点都可看成新的子波波源，它们向各个方向发射球面次波，这些次波经透镜 会聚于 的后焦面上，把接收屏 放在凸透镜 的后焦面上，则由几何光学可知 、 相当于距单缝 无限远。
2夫琅禾费衍射
由光源、衍射屏和接收屏组成的系统，按它们相互间距的大小，将衍射分为两大类。一类是光源和接收屏（或两者之一）距离衍射屏有限的为菲涅尔衍射；另一类是光源和接收屏都距离衍射屏为无限远的夫琅和费衍射[1]。
3实现夫琅和费单缝衍射的几种实验装置
要实现夫琅禾费衍射，必须保证光源到单缝的距离和单缝到衍射屏的距离均无限远（或相当于无限远），但是,把光源及接收屏放在离衍射屏无限远在实际上是做不到的。因此，必须采取相应的措施，才能实际形成夫琅禾费衍射。要使光源距狭缝无限远，实际上可以把光源置于第一个透镜的焦平面上，使之成为平行光束；要使观察屏距狭缝无限远，实际上可以再第二个透镜的焦平面上放置观察屏幕。下面介绍下面将介绍三种形成夫琅禾费衍射的装置[2]。
(a) (b)
图3 两种像面接收装置
Fig.3Two surface receivers
4夫琅禾费衍射图样规律
本实验采用的是如图2所示的远场接受装置,S是波长为 的单色光源，置于透镜 的前焦面上，单色光经透镜 后形成一束平行光投射于狭缝为 的单缝AB上。狭缝上各点可以看成是新的波源，由新的波源向各个方向发出球面次波。这些次波可以看成很多不同方向的平行光束。当衍射屏距离单缝的距离Z满足 ,由惠更斯—菲涅尔原理可推出衍射屏上任意一点 光强 的分布规律为[6]：
可以对L的取值范围进行估算：实验时，若取 ，入射光是 激光，其波长为632.80nm， ，所以只要取 ，就可满足夫琅和费衍射的远场条件。但实验证明，取 ，结果较为理想。
单缝夫琅禾费衍射实验报告(华科版)
2020年春季大学物理实验专业班级：学号： 姓名： 日期：实验名称：单缝夫琅禾费衍射实验目的：观察激光通过单缝后的夫琅禾费衍射现象，测量出单缝宽度实验仪器材料：激光笔、光屏（白纸、墙壁）、卡片（银行卡、校园卡）、直尺、卷尺实验方案（装置）设计：相关理论（公式）、原理图、思路等【夫琅禾费衍射实验原理】：光的衍射通常分为两类：当衍射屏离光源或接收屏的距离为有限远，称为菲涅耳衍射； 当衍射屏与光源和接收屏的距离都是无限远，称为夫琅禾费衍射。
如上图：单缝宽度AB=a ，单缝到接收屏之间的距离是L ，衍射角为Ф 的光线聚到屏上P 点。
设P 点到中央明纹中心距离X K 。
A 、B 出射光线到P 点的光程差则为φsin a 。
当光程差是半波长的偶数倍，形成暗纹。
由于Ф很小，Lax a k /sin =φ即：当λk L ax k =/，时，出现暗纹。
得到单缝宽度：kx Lk a /λ=实验过程：实验步骤、实验现象观察、出现的问题及解决方法等 {一}实验步骤：【1】自制实验器材与装置，并将“狭缝装置”固定于桌面；调整并摆好激光笔的位置，使激光能垂直于狭缝射到远处的墙壁上，并呈现较为清晰的衍射图像；【2】用卷尺测出“狭缝装置”到墙壁的距离L ，重复测量5次，取平均值，并记录数据； 【3】测量暗环中心到中央明纹中心的距离X k ，可选择第1级（k=1）或第2级（k=2）暗纹。
测量5次，取平均值，并记录数据；【4】通过实验原理部分的公式计算出狭缝宽度。
（本实验采用红色激光，红光的波长为650nm ）{二}实验现象的观察：当正确摆好实验装置后，在墙壁上可以观察到，清楚的衍射现象，有亮纹也有暗纹，如下图所示（拍摄效果可能不是很好，见谅）：{三}出现的问题以及解决的方法：（1）问题：开始时，由于并不太了解缝隙要“小”到的程度，所以缝隙宽度太大，无法观察到衍射现象解决：调节缝宽到足够小，即可观察到明显的衍射现象，在1mm 以下，现象比较明显。
夫琅禾费衍射
夫琅禾费衍射摘要：运用数学方法推导了不同孔径夫琅禾费衍射的振幅和光强分布，并作出计算机模拟图，定性定量的研究夫朗禾费衍射的光强分布和图样。
引言光学中的衍射分为近场衍射和远场衍射，而我们在实验室见到的多是远场衍射，即夫琅禾费衍射，所以本文对其进行了进一步研究。
夫琅禾费衍射是平行光入射，所以可以较容易的用数学方法对其研究论证。
本文对不同孔径的夫琅禾费衍射进行了研究，掌握了他们的成像规律才能将其更好的应用在实际生活中。
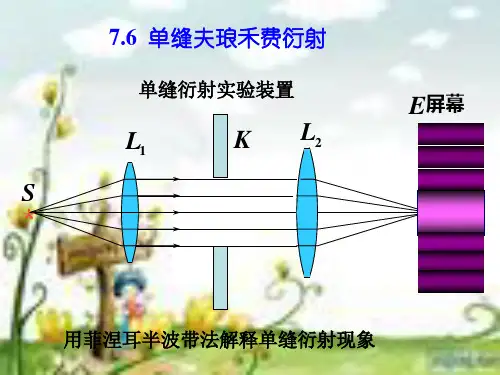
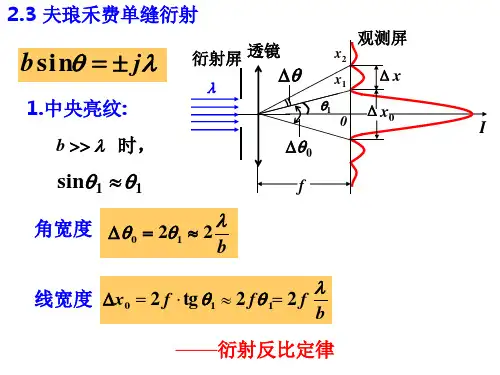
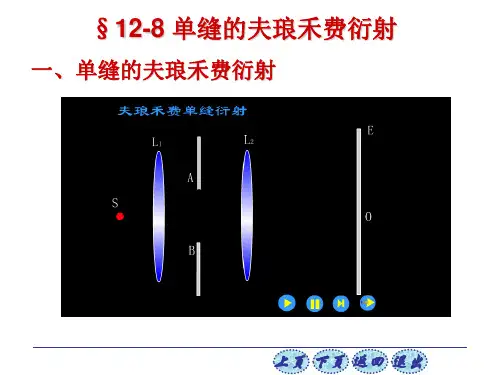
关键词:夫朗禾费衍射 光强分布 计算机模拟 惠更斯-菲涅耳原理 傅里叶变换 1夫琅禾费单缝衍射光强及分布的研究衍射花样的光强分布B'M Bx FP 0PI/I 0光强振幅－3π-2π-ππ2π3π－3π-2π-ππ2π3πy=tguuuy图1 图2当光屏放置在透镜2L 的焦平面上时，屏上出现衍射花样，光强的分布可由u c I I 20sin =式决定，不同的衍射角θ对应于光屏上不同的观察点，首先来决定衍射花样中光强最大值和最小值的位置，即求出满足光强的一阶导数为零的那些点：()2222sin cos sin sin 0u u u u d u du u u -⎛⎫== ⎪⎝⎭ 由此得sin 0,u u tgu ==分别解以上两式，可得出所有的极值点。
1）单缝衍射中央最大值的位置：由sin 0u =，解得满足()00sin /u b πθλ=的那个方向，即0sin θ=0 (中央最大值的位置) （1）也就是在焦点0P 处，200p I =A ，光强为最大。
这里，叠加的各个次波位相差为零，所以振幅叠加相互加强。
2）单缝衍射最小值的位置由sin u =0 ，解得满足 2(s i n )/2k k u b k πθλπ== 的一些衍射方向，即sin k kbλθ=（最小值位置）()1,2,3,k =±±± （2）时，p A 为零，屏上这些点是暗的。
3）单缝衍射次最大的位置在每两个相邻最小值之间有一最大值，这些最大值的位置可由u tgu =这一超越方程解得，我们可以用图解法求得u 的值，作直线y u =和正切曲线y tgu =（图3的下半部），它们的诸交点就是这个超越方程的解：12340, 1.43, 2.463.47, 4.48,u u u u u ππππ==±=±=±=±由此可得分列于中央主最大两边的其他最大值（称为次最大）的位置为()1020300003sin 1.4325sin 2.4627sin 3.4721sin 21,2,k bb bbbbk b k λλθλλθλλθλθ=±≈±=±≈±=±≈±⎛⎫≈±+ ⎪⎝⎭=3) 把这些θ值代入u c I I 20sin =式，可得各最大值光强的比值，若以中央最大的光强20A 为1，即使振幅归一化，则对于10θ,20θ,30θ…处，次最大光强依次为2221230.0472,0.0165,0.0083,A =A =A = 衍射花样最大值与最小值位置沿着垂直于缝长的方向分S(图 3)布，（图3），并由（1）、（2）和（3）三式决定，在居间位置，光强也介乎最大值与最小值之间。
7.6 单缝夫琅禾费衍射解析
( k 1,2 , ) 暗纹 ( k 1,2 , ) 明纹 中央明纹
正、负号表示衍射条纹对称分布于中央明纹的两侧
对于任意衍射角，单缝不能分成整数个半波带，
在屏幕上光强介于最明与最暗之间。
讨论
1. 光强分布 当 增加时,为什么光强的 极大值迅速衰减？
I
5 3 2a 2a
0
(2)由单缝衍射明纹所满足的条件
a sin (2k 1)
第1级明纹所对应的衍射角满足
2
600 109 3 sin (2k 1) (2 1 1) 4 . 5 10 2a 2 0.2 103
600 109 3 sin (2k 1) (2 1 1) 4 . 5 10 2a 2 0.2 103
第一级暗纹 k=1,1=300
a
sin 1
0.5 2 1.0m
例、一束波长为 =5000Å的平行光垂直照射在一个 单缝上。(2)如果所用的单缝的宽度a=0.5mm，缝后 紧挨着的薄透镜焦距f=1m，求：(a)中央明条纹的角 宽度；(b)中央亮纹的线宽度；(c) 第一级与第二级暗 纹的距离； (a)
3 2a
5 sin 2a
当 角增加时，半波带数增加，未被抵消的半 波带面积减少，所以光强变小； 另外，当： K ( ) I
2. 中央亮纹宽度
中央两侧第一暗条纹之间的区域，称做零极 （或中央）明条纹，它满足条件：
I
a
a sin
a 3 2a 5 sin 2a
a sin 2k
2
k 1
则
a sin0
夫琅禾费单缝衍射
焦距 f 为：
(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m
[B]
矩形孔的夫琅禾费衍射
两个正交迭置的狭缝（设宽度分别为a、b） 衍射光在x, y方向的衍射角分别为
x, y
衍射光场：两个按正交方向展开的单缝衍射场的乘积
I(P)
I
0
s i n
2
s i n
2
远去的汽车头灯
最小分辨角：
S1
D
*
1
1.22
D
* S2
0 I
表达式中的波长 是指衍射光场在像方空间所处介质
中的波长
眼睛（正常人眼） a=D/2=1mm，n=1，n'=1.336，
0=550nm，f '=2.2cm
角分辨极限： m=0.610/n'a ≈2.511×10-4 rad
线分辨极限：
0m=0.610/na ≈3.355×10-4 rad
分辨本领:
1 R
min
光学系统对被观察对象微小细节的分辨能力
These photographs of an automobile’s headlights were taken at the greater and greater distances from the camera.
远去的汽车头灯
两个按正交方向展开的单缝衍射场的乘积衍射光在xy方向的衍射角分别为其中矩形远场衍射振幅三维图矩形孔的夫琅禾费衍射图样矩形远场衍射强度三维图24设圆孔的直径为d与p点对应的衍射角为衍射屏观察屏中央亮斑爱里斑变小第一暗圈所包围的中央亮斑叫做爱里斑airydisk线半径
2.3 夫琅禾费单缝衍射
bsin j
(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m
[B]
矩形孔的夫琅禾费衍射
两个正交迭置的狭缝（设宽度分别为a、b） 衍射光在x, y方向的衍射角分别为
x, y
衍射光场：两个按正交方向展开的单缝衍射场的乘积
I(P)
I
0
s i n
2
s i n
2
远去的汽车头灯
最小分辨角：
S1
D
*
1
1.22
D
* S2
0 I
表达式中的波长 是指衍射光场在像方空间所处介质
中的波长
眼睛（正常人眼） a=D/2=1mm，n=1，n'=1.336，
0=550nm，f '=2.2cm
角分辨极限： m=0.610/n'a ≈2.511×10-4 rad
线分辨极限：
0m=0.610/na ≈3.355×10-4 rad
分辨本领:
1 R
min
光学系统对被观察对象微小细节的分辨能力
These photographs of an automobile’s headlights were taken at the greater and greater distances from the camera.
远去的汽车头灯
两个按正交方向展开的单缝衍射场的乘积衍射光在xy方向的衍射角分别为其中矩形远场衍射振幅三维图矩形孔的夫琅禾费衍射图样矩形远场衍射强度三维图24设圆孔的直径为d与p点对应的衍射角为衍射屏观察屏中央亮斑爱里斑变小第一暗圈所包围的中央亮斑叫做爱里斑airydisk线半径
2.3 夫琅禾费单缝衍射
bsin j
12-8单缝的夫琅禾费衍射
f
x0
2f
tan 1
2 f 12f来自aaB. 次极大
x
f
a
1 2
x0
前提仍然是很小
上页 下页 返回 退出
缝宽变化对条纹的影响
由
x
f
a
1 2
x0
知，缝宽越小，条纹宽度越宽
I
0
sin
当 a 时，
当 a 时，0
x ，此时屏幕呈一片明亮；
，x此时0屏幕上只显出单
一的明条纹单缝的几何光学像。
∴几何光学是波动光学在/a0时的极限情形
b
b
b
3 f 2 f f
bbb
f 2 f 3 f x
b
上页
下页b
返回
退b 出
衍射图样 衍射图样中各级条纹的相对光强如图所示.
1 I / I0 相对光强曲线
0.017 0.047
0.047 0.017
-2( /a) -( /a) 0 /a 2( /a) sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称 次极大。 中央极大值两侧的各极小值称暗纹。
(P处干涉相消形成暗纹)
上页 下页 返回 退出
2.明暗纹条件
由半波带法可得明暗纹条件为：
a sin 2k k 1，2，3，L ——暗纹
2
a sin 2k 1 k 1，2，3，L
2
——明纹(中心)
asin 0
——中央明纹(中心)
上述暗纹和中央明纹(中心)的位置是准确的，其余 明纹中心的实际位置较上稍有偏离。
上页 下页 返回 退出
明纹宽度
A. 中央明纹
当 a 时 ， 1 级暗纹对应的衍射角
关于夫琅禾费单缝衍射实验教学研究的文献综述
关于夫琅禾费单缝衍射实验教学研究的文献综述1引言光的衍射现象是光波动性的一个主要标志，也是光波在传播过程中的最重要属性之一，光的衍射在近代科学技术中占有极其重要的地位。
光的单缝衍射实验是光学中非常重要的一个实验，但是在实验教材描述比较简单，学生未能全面掌握操作技巧，实验时存在一些重要的实际操作问题，在教学中学生经常会遇到一些容易忽视但又十分重要的问题。
通过对夫琅禾费单缝衍射实验前的实验设计、实验过程中的控制和监视、实验后数据的深入分析，不仅为学生掌握衍射方面的知识提供准确的实验参考依据，为教师教学质量的提高起到一定的作用，而且也可以为学生实验提供实验参考，提高实验的效率，培养学生的实验操作能力，分析和探究问题的能力。
2研究的发展与现状2.1夫琅禾费衍射发展与现状关于光发生的衍射的具体机理及规律，惠更斯提出了次波说，惠更斯认为：任何时刻波面上的没一点都可以作为次波的波源，各自发出的球面次波；在以后的任何时刻，所有这些次波波面的包络面形成整个波在该时刻的新的波面。
但是惠更斯次波说不涉及波的时空周期特性—波长、振幅和相位，因而不能说明在障碍物的边缘波的传播方向偏离直线的现象。
菲涅耳对惠更斯的原理进行了改进，补充描述了次波的基本特性—振幅和相位的定量表达式，并增加了“次波相干叠加”的原理，以严密的数学，推导出严密的数学推理导出了菲涅耳衍射积分，发展成为了惠更斯—菲涅耳原理，但是由于此积分式相当复杂，历史上对于此积分的进一步研究，只是选取了几种几何形状较简单的开孔和障碍物，并且是在相对于孔径法线对称的前提下来进行推导和演示的，如：单缝、圆孔、园屏等，结果能圆满地解释光的衍射现象。
麦克斯韦在1865年的理论研究中指出，电磁波以光速传播，说明光是一中电磁现象。
这个理论在1888年赫兹在实验室证实。
至此，确立的光的电磁理论基础，光的电磁理论发展起来后，基尔霍夫从波的微分方程出发，利用场论中的格林函数得到了基尔霍夫衍射公式：01(P )(GU )4U G U ds n n π∑∂∂=-∂∂⎰⎰ ，基尔霍夫衍射公式可以给出与实际符合很好的结果，因而在实际中得到广泛的应用。
多缝的夫讲义琅禾费衍射
I
N2
由上讨论可知：
0 12
n
N4
当相邻缝间距d 一定时，多
缝干涉和双缝干涉明纹间隔 都是一样的（与N无关）。
n 0 1 234
随着缝数的增加，明条纹变 得越细、越亮，而明条纹之
N6
间是大片暗区。
n 0 1 2 34 5 6
3、单缝衍射因子对多缝干涉的影响、缺级：
当α=±k'π （k'= 1, 2, 3, …)
aθ δ
θ
A assiN i n na0(sin )(ssiN i n n) 其中
a sin
ΔL
II0(sin)2(ssiiN nn)2
d sin
单缝衍射因 子
缝间干涉因子
2、缝数N对多缝干涉条纹的影响（多缝使条纹细而明亮）：
⑴ 主极大（明条纹中心）：
当 dsink 即 22k时：
解：
⑴ dab2 即 2， 4 缺 级
aa
所以单缝衍射中央明纹内有3条干涉明纹：0、±1级明纹。
⑵ 因为： d b a d s i n a s i n
多缝干涉因子： (ssiiN n n)2(ssii2 n n)2(2co )s2
I I 0 (si) 2 ( n s sN ii) n 2 n I 0 (si) 2 ( n 2 co ) 2 4 s I 0 (s 2 2 i) n 2
k=0
k=4 k=3
k = -2
k=2
k = -1 k = 1
-90°-80°-70°-60°-50°-40°-30°-20°-10° 0° 10° 20° 30° 40° 50° 60° 70° 80° 90°
3、光栅的分辨本领：
光学基础光的干涉与衍射的现象与计算
光学基础光的干涉与衍射的现象与计算光的干涉与衍射是光学中的重要现象，我们可以通过这些现象来理解光的性质和传播规律。
本文将介绍光的干涉与衍射的概念、原理以及计算方法。
一、干涉的概念与现象干涉是指两束或多束光相遇时所产生的相互作用现象。
干涉的本质是光波的叠加，当两束光波相遇时，它们会相互叠加并产生明暗交替的干涉条纹。
干涉现象可以通过Young双缝实验来观察。
Young实验中，将一块狭缝板放在光源前方，形成两个狭缝，然后让光通过这两个狭缝，形成两个相干光源。
当这两个光源发出的光在屏幕上相遇时，就会出现干涉条纹。
干涉条纹的出现是因为两个光波在相遇点处发生干涉，相长干涉会产生亮条纹，相消干涉会产生暗条纹。
二、干涉的计算方法干涉计算的关键是求出相邻两条干涉条纹之间的光程差。
干涉条纹之间的光程差决定了干涉条纹的间距和亮暗程度。
光程差的计算公式为：Δ = d * sinθ其中，Δ为光程差，d为两个狭缝之间的距离，θ为入射光线与平行光束的夹角。
在Young实验中，干涉条纹的间距可以用以下公式计算：λ = Δy / L其中，λ为干涉条纹间距，Δy为相邻两个亮条纹的间距，L为屏幕与狭缝板的距离。
三、衍射的概念与现象衍射是指当光波通过一个或多个小孔或物体边缘时，波的传播方向发生改变的现象。
衍射现象是光波的波动性质的表现，它使光线呈现出扩散的特点。
衍射的经典实验是夫琅禾费衍射实验。
在夫琅禾费衍射实验中，光通过一个狭缝后，形成一个光源的小孔。
当这个光源的小孔和屏幕距离较远时，我们可以观察到在屏幕上的衍射图样。
衍射图样的形状决定于狭缝的尺寸和光的波长。
四、衍射的计算方法衍射计算同样需要求解光程差，以确定衍射图样的形状和大小。
单缝衍射中，衍射角的计算公式为：θ = λ / a其中，θ为衍射角，λ为入射光波的波长，a为缝宽。
衍射的主极大和次极大的位置可以用以下公式计算：y(m) = m * λ * L / a其中，y(m)为第m个极大处的位置，L为缝到屏幕的距离。
2_6夫琅禾费单缝衍射
屏幕 屏幕
S
*
3
2.6.2 强度的计算 x
屏幕
dx
r
θ
r0
P
B
S
F1
x
λ
Δ = x sin θ
M N 0 D B′
P0
θ
宽度dx窄带所发次波振幅
将波前 BB′分割成许多等宽窄带dx, 初位相 ϕ0 = 0
A0 dx A0 整个狭缝所发次波振幅； b A0 dx cos ωt M点所发次波的振动 dE0 = b
πb sin θ λ
λ
次最大光强的角位 置近似为：
sin θ k 0
2
2k + 1 λ ≈± 2 b
⎛ sin u ⎞ 代入单缝衍射因子 I = ⎜ ⎟ I 0 各次最大的光强为： ⎝ u ⎠
I10 = 0.0472 I 0
I 20 = 0.0165 I 0
I 30 = 0.0083I 0
10
可见，衍射级次越高，光强就越小。次最大的光 强最大不到中央最大值的1/20，并且随着级数的增 加而很快减小。 光强曲线
1.0
I I0
− 3π
− 2π
−π
0
π
2π
u
11
2.6.4 单缝衍射图案的特点
(1)、各级最大值的光强不相等，随着级数k的增 大而减小。中央最大值的光强最大（主最大）， 次最大值远小于中央最大值 Ｉ１０< 0.05Ｉ０ (2)、角宽度 规定以相邻暗纹的角距离作为其间条纹的角宽度。 在近轴条件下， θ很小， sinθ ≈θ ， 由暗纹的角位置公式 sin θ k ≈ θ = k
~ A0 dx 其复振幅为 dE = e b
i
2π
夫琅禾费单缝衍射光强分析与探讨 修改
夫琅禾费单缝衍射光强分析与探讨摘要：在夫琅禾费单缝衍射实验中,如果在透镜的物方焦面内沿着某一圆周改变光源S的位置,让透镜出射的单色平面光波都以相同的入射角H0入射到单缝衍射屏上,则单缝衍射光强分布均会发生改变,说明衍射图样的光强分布不仅和入射角H0以及衍射角H有关,而且和光源S的位置有关;考虑单缝衍射屏上光波相位的分布和平面光波的入射方位(即光源S的位置)的关系,采用矢量图解法对单缝衍射因子进行分析及计算,得到了全面的夫琅禾费单缝衍射光强公式。
关键词：单缝衍射;光强;光程差;斜入射目录1 夫琅禾费单缝衍射（一） (1)的物方焦点时的装置及现象 (1)1.1 单色点光源S位于透镜L11.2 用积分法来求夫琅禾费单缝衍射的光强………………………………（）1.3 衍射光强的极值分布条件及特点………………………………………（）2 夫琅禾费单缝衍射（二）……………………………………………………（）2.1 单色点光源S位于透镜L的物方焦面上时的装置……………………（）12.2 单缝衍射因子分析及计算………………………………………………（）3 总结…………………………………………………………………………（）1 夫琅禾费单缝衍射（一）1.1 单色点光源S位于透镜L的物方焦点时的装置及现象1如图1所示,单色点光源S置于凸透镜L1的物方焦平面上,从点光源发出的光经过透镜以后变成平行光,垂直射到宽度约为十分之几毫米的狭缝上。
缝后置一凸透镜L2,在L2象方焦平面上放置接收屏,则屏上显现出由一系列不连续的明亮短线组成的衍射图样,如图1[1]所示。
改变缝的宽度,衍射图样也发生变化,缝越宽,衍射图样越收缩,当缝宽足够大时(远大于波长),则衍射图样缩成一点,这就是点光源S在透镜中所成的象。
狭缝对光波在方向上的限制,使光在x方向上产生衍射,生成一系列沿x方向排列的明亮的短线,这些短线好像是点光源的一个扩展开的象。
如果用氮生在光器作为光源,则可以把透镜L1去掉,使激光直接照射在单缝上,并且去掉L2,在缝后足够远处(几米)屏上可观察到夫琅禾费衍射图样。
大学物理第十七章波动光学(九)单缝的夫琅禾费衍射
u
I
I
0
(
sin u
u
)2
式中I0 ( NA1 )2为中央明纹光强
作光强曲线，令 I 0得极值位置 u
明纹： 暗纹：
sin 0,1.43 ,2.46 ,
a
a
sin
a
,
2
a
,
3
a
,请与半波带法比较
谢谢欣赏!
θ≠0，衍射光线汇集于L2的焦平面上某点P δ≠0 P处光强可由菲涅耳公式计算
介绍确定P光强的两种简便方法 菲涅耳波带法
振幅矢量叠加法
二、菲涅耳半波带法（半定量方法）
衍射角为的一束平行
光线的最大光程差：
AC asin
a
用 去分，设 k
2
2
对应的单缝a被分为
A A1
暗纹
二级 一级 中央明纹 暗纹 暗纹
一级 明纹
二级 明纹
3
2
a
a
a
0
3
a 2a
sin
5
2a
2
2
2
22
2
暗纹公式中，k＝0，δ＝0，为中央明纹中
心，不是暗纹
明纹公式中，可k＝0， δ＝λ/2，仍在中央明纹区, 不是明纹中心
（3）暗纹和中央明纹位置精确，其他明纹位置只 是近似
其次包含着放大，a越小， Δθ越大，是一种 光学变换放大，这正是激光测径和衍射用于物质 结构分析的基本原理。
当a》λ时，Δθ＝0，几何投影斑，过渡 到几何光学（a＝103 λ以上）
当a＝10λ－ 103 λ时，衍射显著
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用cos(a b) cosa cosb sina sinb, 有
2
E c'
a 2 a 2
2 2 t L0 ) cos( x sin ) cos( 2 sin( t L0 ) sin( x sin ) dx 2
缝 透 平 镜 面 L1 S 透 镜 L2 观 察 屏 p ·
*
f1
a
S：单色线光源
0
a: 单缝缝宽
： 衍射角, P点
与透镜中心连线 与光轴的夹角
f2
§11-2 夫琅禾费单缝衍射
单缝衍射图样
sin
一组与缝平行的明暗相间的直条纹, 在与狭缝垂直的方向上扩展 开. 中央是最明亮的条纹, 两边对称分布着一系列强度较弱的宽 度相等的条纹, 中央明条纹宽度是其两侧明条纹宽度的两倍.
定义： 光在传播过程中能绕过障碍物的边缘 而偏离直线传播的现象叫光的衍射。
障碍物的尺寸是否与波长具有可比较性, 是否相干光源. 声波的衍射随处可见, 但光波的较少.
§11-1 衍射现象、惠更斯-菲涅耳原理
二. 衍射分类：
光源 S
障碍物
观察屏
*
L
B
D
P
（1）菲涅耳衍射: L 和 D中至少有一个是有限值。 （2）夫琅禾费衍射: L 和 D皆为无限大, 即照射
第十一章 光的衍射
§11-1 衍射现象、惠更斯——菲涅耳原 理 §11-2 夫琅禾费单缝衍射 §11-4 夫琅禾费圆孔衍射、 光学仪器的分辨本领
§11-1 衍射现象、惠更斯-菲涅耳原理
§11-1 衍射现象、惠更斯-菲涅耳原理
一. 衍射现象
衍射屏 观察屏 衍射屏 观察屏 L L
*
S
a
S
a< 10 3
a sin E c' a cos( t ), 其 中
光强正比于振幅的平方, 所以
§11-2 夫琅禾费单缝衍射
二 . 强度的计算 透镜 x
设缝长l, 缝宽a, 观测屏 以缝中心为原点 p 建立坐标系. 在x a L 2 处取宽度为dx的 x , dx L0 P0 平行于缝的长条 O z C a 面元dS, dS=ldx 2 f P点的光振动是衍射角 为θ 的平行光的汇聚点. 设O点到P点的光程为L0, 考虑透镜的等光程原理, 则过x点的面元dS的光线到P点的光程为L0-xsinθ dS面元发出衍射光在P点的元振动为
到障碍物上的入射光和离开障碍物的衍射光 都是平行光. 在实验中可以用透镜得到.
§11-1 衍射现象、惠更斯-菲涅耳原理
圆孔的衍射图样：
屏上 图形
孔的投影 菲涅耳衍射 夫琅禾费衍射
§11-1 衍射现象、惠更斯-菲涅耳原理
刀片边缘的衍射
障碍物为小圆盘 (硬币)时的衍射
（泊松亮点）
§11-1 衍射现象、惠更斯-菲涅耳原理
三. 惠更斯—菲涅耳原理
波传到的任何一点都是球面子波的波源 ( 惠更斯 ) ， 各子波在空间某点的相干叠加(菲涅耳子波干涉)， 就决定 了该点波的强度。
n dS
· Q
rቤተ መጻሕፍቲ ባይዱ
波面上每一个面元dS都可 dE(p) 以看成是发射子波的波源, 发出球面子波, 它传到波 p 面前方某一点P的元振动:
·
S(波前)
§11-2 夫琅禾费单缝衍射
二 . 强度的计算
P点的合振动为
E cl
a 2 a 2
E0 2 K ( ) cos[ t ( L0 x sin )]dx L0
P点的合振动近似积分为: a 2 2 2 E c' a cos[( t L0 ) x sin ] dx
n dS
· Q
r
P点的合振动是整个波面 dE(p) S上各面元所引起的振动 的叠加, 得到惠更斯—菲 p 涅耳原理的解析表达式:
·
S(波前)
E0 2 E c K ( ) cos( t r 0 ) dS S r
§11-2 夫琅禾费单缝衍射
§11-2 夫琅禾费单缝衍射
一 . 实验装置和现象
z
E0dS 2 d E cK ( ) cos( t r) r
近轴条件下,θ 和L的变化都很小,K(θ)和振幅分母中的 r可近似为常数,但相位中的r不近似. P点的合振动为:
E cl
a 2 a 2
E0 2 K ( ) cos[ t ( L0 x sin )]dx L0
§11-2 夫琅禾费单缝衍射
二 . 强度的计算
P点的合振动近似积分为: a 2 2 2 E c' a cos( t L0 ) cos( x sin ) 2 与被积变量 2 2 sin( t L0 ) sin( x sin ) dx 无关,常数 奇函数, 积分出零
复习学过的部分
声波: 人听觉可感知频率范围: 20Hz – 20000 Hz 空气中声速: 340m/s 空气中波长: 17 m – 0.017m(1.7cm) 次声波: f < 20Hz, 波长>17m 超声波: f >20000Hz, 波长<1.7cm 光波: 人视觉可感知频率范围: (3.9-7.7) ×1014Hz (10) 空气中光速: 3×108m/s (6) 空气中波长: 3.9×10-7 m – 7.6 ×10-7 m (5) 红外光波: f < 3.9×1014 Hz 紫外光波: f > 7.7×1014 Hz
E0dS 2 d E cK ( ) cos( t r 0 ) r
其中: K(θ)倾斜因子, 随θ增大缓慢减小, θ≥900时取零.
§11-1 衍射现象、惠更斯-菲涅耳原理
三. 惠更斯—菲涅耳原理
波传到的任何一点都是球面子波的波源 ( 惠更斯 ) ， 各子波在空间某点的相干叠加(菲涅耳子波干涉)， 就决定 了该点波的强度。
E x dS 2 d E cK ( ) cos( t r 0 ) r
§11-2 夫琅禾费单缝衍射
二 . 强度的计算
平面波入射, 缝为 等位相面, 振幅E0, 设初相为0, dS面 元发出衍射光在P 点的元振动为
x
x , dx
a 2
透镜
观测屏
L L0
p
f P0
a 2
O
C