物理学中的对称性PPT课件

物理学中的对称性原理物理学是研究物质、能量和它们之间相互作用的学科，而对称性原理则是物理学中最为基本的一条规律。

对称性原理指出，在自然界中，许多物理现象都与对称性相关，基本上可以归纳为几种对称性：空间对称性、时间对称性、粒子对称性等。

本文将介绍这些对称性及其在物理学中的应用。

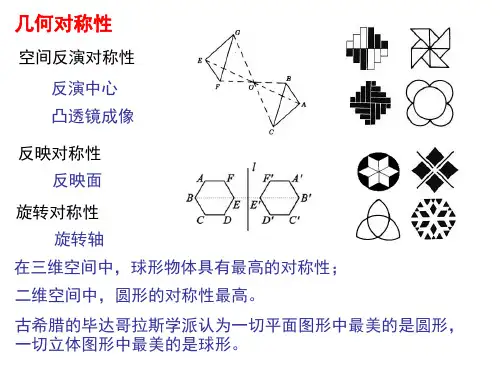
空间对称性空间对称性是指三维空间中的物理过程在经过旋转、平移、镜面反射等操作后，物理定律依旧保持不变。

以旋转对称性为例，自然界中的物理过程在经过旋转操作后，不论几度旋转，物理规律都保持不变。

例如，一个自转着的天体，无论自转轴怎样旋转，自转速度都保持不变。

旋转对称性也是描述物体角动量守恒的重要原理之一。

时间对称性时间对称性是指自然界中的物理过程在经过时间反演操作后，物理定律仍然保持不变。

这个原理在物理学中有重要的应用，例如，在实验室中进行的物理实验与在天文观测中观测到的物理现象，经过时间反演操作后，物理规律都保持不变。

另外，时间对称性也是研究物理过程的稳定性和不稳定性的基础。

粒子对称性粒子对称性是指自然界中的基本粒子都具有某种对称性。

例如，电子和正电子的基本物理量完全相同，但它们的电量和质量互为相反数，这种对称性称为电荷共轭对称性。

这个原理也可以解释为物理定律关于粒子和它们的反粒子具有相同的对称性。

粒子对称性在研究基本粒子物理学中有重要的应用，例如，粒子对称性异常破缺现象可以解释基本粒子间的相互作用。

对称性原理的应用对称性原理在物理学中的应用非常广泛。

例如，它可以解释光子不具有电荷和磁荷的原因，以及在标准模型中解释基本粒子种类的数量和它们之间的相互作用。

在物理学中，对称性原理往往是推导新理论的重要起点，新理论应该符合对称性原理，从而向实验和观测提出了新的挑战和测试。

除此之外，对称性原理还在宇宙学和天体物理学中应用广泛。

它可以帮助人们理解宇宙的演化历史，解释黑洞中的物理现象，以及探究暗物质的性质。

结语对称性原理是物理学的基本规律之一，它描述了自然现象中的对称性和不对称性。

物理学中的对称性原理物理学中的对称性原理是指在自然界中存在着各种对称性，并且这些对称性对于物理定律的描述和解释起着重要的作用。

对称性原理是物理学中的基本原理之一，它帮助我们理解和解释了许多重要的现象和规律。

一、空间对称性空间对称性是指物理系统在空间变换下保持不变。

在三维空间中，常见的空间对称性有平移对称性、旋转对称性和镜像对称性。

1. 平移对称性：物理系统在空间平移下保持不变。

例如，一个自由粒子在空间中运动时，其动能和势能在空间平移下保持不变。

2. 旋转对称性：物理系统在空间旋转下保持不变。

例如，一个均匀的圆盘在绕其对称轴旋转时，其物理性质保持不变。

3. 镜像对称性：物理系统在空间镜像变换下保持不变。

例如，一个球在经过镜像变换后，其形状和物理性质保持不变。

二、时间对称性时间对称性是指物理系统在时间反演下保持不变。

时间反演是指将时间t变为-t，即将物理系统的演化方向反转。

时间对称性原理表明，物理定律在时间反演下保持不变。

1. 动力学时间对称性：物理系统的演化方程在时间反演下保持不变。

例如，牛顿第二定律F=ma在时间反演下仍然成立。

2. 热力学时间对称性：热力学系统的热平衡状态在时间反演下保持不变。

例如，一个封闭的热力学系统在达到热平衡后，其热平衡状态在时间反演下保持不变。

三、粒子对称性粒子对称性是指物理系统在粒子变换下保持不变。

粒子变换是指将一个粒子变为另一个粒子，例如将一个电子变为一个中子。

粒子对称性原理表明，物理定律在粒子变换下保持不变。

1. 电荷守恒：电荷在粒子变换下保持守恒。

例如，一个粒子和其反粒子的电荷之和为零。

2. 弱力相互作用：弱力相互作用在粒子变换下保持不变。

例如，一个粒子在弱力相互作用下可以转变为另一种粒子。

四、规范对称性规范对称性是指物理系统在规范变换下保持不变。

规范变换是指改变物理系统的规范场，例如改变电磁场的规范。

规范对称性原理在量子场论中起着重要的作用。

1. 电磁规范对称性：电磁场的规范变换不改变物理系统的物理性质。

物理学中的对称性原理在物理学中，对称性原理是一项非常重要的基础理论，它在描述自然界中各种物理现象和规律时起着至关重要的作用。

对称性原理是指在物理学中，系统的性质在某种变换下保持不变的性质。

这种不变性可以帮助我们理解和预测自然界中发生的各种现象，从微观粒子到宏观宇宙，对称性原理都贯穿其中。

一、空间对称性空间对称性是指系统在空间平移、旋转或镜像变换下保持不变的性质。

在物理学中，空间对称性是非常重要的，因为它可以帮助我们理解空间中的各种物理规律。

例如，牛顿定律在空间平移下是不变的，这意味着物体的运动不受空间位置的影响。

另外，电磁场的麦克斯韦方程组也具有空间对称性，这表明电磁场的性质在空间变换下保持不变。

二、时间对称性时间对称性是指系统在时间平移下保持不变的性质。

在经典力学中，牛顿定律具有时间对称性，这意味着物体的运动不受时间的影响。

另外，热力学第二定律也具有时间对称性，这表明热力学系统在时间变换下保持不变。

三、粒子对称性粒子对称性是指系统在粒子变换下保持不变的性质。

在粒子物理学中，粒子对称性是非常重要的，因为它可以帮助我们理解粒子之间的相互作用。

例如，电荷守恒定律表明系统在电荷变换下保持不变，这意味着电荷是守恒的。

另外，弱相互作用的手性对称性也是粒子对称性的一个重要例子。

四、规范对称性规范对称性是指系统在规范变换下保持不变的性质。

在现代物理学中，规范对称性是描述基本相互作用的重要工具。

例如，电磁相互作用和强相互作用都可以通过规范对称性来描述。

规范对称性的破缺可以导致粒子获得质量，从而形成物质的结构。

五、对称性破缺在物理学中，对称性破缺是指系统在某些条件下失去对称性的现象。

对称性破缺可以导致一些新的物理现象的出现，例如超导现象和弱相互作用的手性破缺。

对称性破缺也是现代物理学中一个重要的研究课题，它可以帮助我们理解自然界中复杂的现象和规律。

总结起来，对称性原理在物理学中扮演着非常重要的角色，它帮助我们理解自然界中的各种现象和规律。

物理学中的对称性物理学是一门研究自然界基本规律和物质运动的学科。

而对称性是物理学中一个非常重要的概念。

无论是经典物理学还是现代物理学，对称性都在理论研究和实验观测中扮演着重要的角色。

本文将介绍物理学中的对称性以及对称性在各个物理领域的应用。

一、对称性概述对称性是物理学中的基本原理之一，它描述了系统在某种变换下的不变性。

具体来说，对称变换是指对于某个系统，在进行某种操作后系统的性质保持不变。

物理学中常见的对称变换包括平移、旋转、空间反演、时间反演等。

对称性可以分为离散对称性和连续对称性。

离散对称性是指系统在进行某种操作后仅有有限个不同状态，如镜面对称性；而连续对称性则是指系统在进行某种操作后可以无限变换，如旋转对称性。

二、对称性在力学中的应用在物理学的力学领域，对称性是非常重要的概念之一。

牛顿力学中的动量守恒和角动量守恒定律，都是基于系统的对称性得出的。

例如，在没有外力作用下，系统的动量守恒的定律可以由空间平移对称性推导而来。

此外，对称性还可以用于解释一些自然现象。

比如，质点在匀速直线运动时，其运动轨迹可以通过时间平移对称性的描述。

而在刚体动力学中，对称性则可以帮助我们分析和预测刚体的运动规律。

三、对称性在电磁学中的应用电磁学是物理学中的一个重要分支，对称性在电磁学中的应用非常广泛。

电磁场的麦克斯韦方程组在形式上是具有非常强的对称性的，它们满足洛伦兹对称性。

这种对称性不仅能够揭示电磁场的基本规律，还为电磁波的传播提供了坚实的理论基础。

此外，对称性还可以帮助我们理解一些电磁现象。

例如，光学中的折射现象可以通过平移对称性进行解释。

光线从一个介质传播到另一个介质时，能量守恒要求入射角和折射角满足一定的关系，这个关系正是由折射率和介质对称性决定的。

四、对称性在量子力学中的应用量子力学是研究微观粒子行为的理论，对称性在量子力学中也有着重要的应用。

量子力学中的对称性表现为对称变换下的波函数不变。

例如，在自旋的描述中，波函数在空间旋转下是不变的，这意味着自旋系统具有旋转不变性。

物理学中的对称性与守恒定律在物理学中，对称性和守恒定律是两个核心概念。

对称性是自然界中普遍存在的特征，而守恒定律则是对自然界中物质和能量守恒的描述。

这两个概念相互关联，共同构成了物理学中一个重要的研究领域。

一、对称性在物理学中的应用对称性在物理学中有着广泛的应用。

最为人熟知的是空间对称性和时间对称性。

空间对称性指的是在空间中的各个位置上具有相同的物理性质。

例如，在宇宙中，无论你身处何地，都能感受到相同的万有引力。

这就是空间对称性的体现。

时间对称性则是指物理规律在时间上的不变性。

举个例子，考虑一个摆钟，不管时间如何推移，它的摆动周期是恒定不变的。

这也是时间对称性的一个例证。

除了空间对称性和时间对称性外，物理学中还涉及其他形式的对称性，如粒子对称性、守恒粒子数等。

这些对称性的研究，对于我们理解自然的基本规律以及发展新的物理理论都具有重要意义。

二、守恒定律和对称性的关系守恒定律是物理学中的基本原理之一。

它可以从对称性中推导得出。

根据诺特定理，每个连续对称性都对应一个守恒量。

以动量守恒定律为例，物理系统中的动量守恒是因为系统在空间平移对称性下具有不变性。

也就是说，无论系统在空间中的位置如何变化，系统的总动量保持不变。

类似地，能量守恒定律是由时间平移对称性推导得出的。

无论时间如何变化，系统的能量总是保持不变。

这种对称性与守恒定律的关系，使我们能够通过对系统中的对称性进行研究，来预测和解释物理学中的现象和规律。

三、对称性破缺与守恒量的消失尽管对称性在物理学中扮演着重要的角色，但有时我们也会观察到对称性的破缺。

对称性的破缺通常意味着守恒定律不再适用。

著名的例子是弱相互作用中的手性问题。

在弱相互作用中，左手和右手的粒子行为有所不同，这打破了空间反演对称性。

通过对这个对称性破缺的研究，我们可以更好地理解物理学中的基本粒子和相互作用。

此外，在高能物理实验中，科学家们也发现了很多新的物理现象。

这些现象通常涉及到对称性的破缺，以及新的守恒定律的出现。