2019年第十四届华罗庚金杯少年数学邀请赛决赛.doc

历年华罗庚金杯试题第一届“华罗庚金杯”少年数学邀请赛初赛试题1．1966、1976、1986、1996、2006这5个数的总和是多少？2．每边长是10厘米的正方形纸片，正中间挖一个正方形的洞，成为一个宽度是1厘米的方框。

把5个这样的方框放在桌面上，成为这样的图案。

问桌面上被这些方框盖住的部分面积是多少平方厘米？3．105的约数共有几个？4．妈妈让小明给客人烧水沏茶。

洗开水壶要用1分钟，烧开水要用15分钟，洗茶壶要用1分钟，洗茶杯要用1分钟，拿茶叶要用2分钟。

小明估算了一下，完成这些工作要花20分钟，为了使客人早点喝上茶，按你认为最合理的安排，多少分钟就能沏茶了？5．右面的算式里，4个小纸片各盖住了一个数字。

被盖住的4个数字总和是多少？6．松鼠妈妈采松籽。

晴天每天可以采20个。

有雨的天每天只能采12个。

它一连几天采了112个松籽，平均每天采14个。

问这几天当中有几天有雨？7．边长1米的正方体2100个，堆成一个实心的长方体。

它的高是10米，长、宽都大于高。

问长方体的长与宽的和是几米？8．早晨8点多钟，有两辆汽车先后离开化肥厂，向幸福村开去。

两辆汽车的速度都是每小时60公里。

8点32分的时候，第一辆汽车离开化肥厂的距离是第二辆汽车的3倍。

到了8点39分的时候，第一辆汽车离开化肥厂的距离是第二辆汽车的2倍．那么，第一辆汽车是8点几分离开化肥厂的？9．有一个整数，除300、262、205，得到相同的余数．问这个整数是几？10．甲、乙、丙、丁4个人比赛乒乓球，每两个人都要赛一场．结果甲胜了丁，并且甲、乙、丙3个胜的场数相同．问丁胜了几场？11．两个十位数1111111111和9999999999的乘积有几个数字是奇数？12．黑色、白色、黄色的筷子各有8根，混杂地放在一起。

黑暗中想从这些筷子中取出颜色不同的两双筷子。

问至少要取多少根才能保证达到要求？13．有一块菜地和一块麦地，菜地的21和麦地的31放在一起是13亩，麦地的21和菜地的31放在一起是12亩，那么，菜地是几亩？14．71427和19的积被7除，余数是几？15．科学家进行一项实验，每隔5小时做一次记录．做第十二次记录时，挂钟的时针恰好指向9，问做第一次记录时，时针指向几？16．有一路电车的起点站和终点站分别是甲站和乙站。

第十四届华罗庚金杯少年数学邀请赛决赛试题C参考答案(初一组一、填空(每题l0分，共80分题号 1 2 3 4 5 6 7 8③答案二、解答下列各题(每题l0分，共40分，要求写出简要过程9．答案：26．解答：因为和是直角三角形且AC=2MC、BC=2NC，我们有：，，等式两边对应相加，结合也是直角三角形，得到：，所以：，．评分参考：1列出前两个等式得4分；2列出第三个等式得4分；3给出正确结果得2分．10．答案：每小时120千米．解答：设甲和乙车速度分别是每小时和千米，甲和乙到达C地的时间分别是小时和小时．则：，化简得：，，．所以甲车速度是每小时l20千米．评分参考：1列出一个方程给2分，共6分；2给出正确结果得4分．11．答案：．解答：设有负数根，则，进而．要保证为负数，必须满足．设有正数根，则，进而．要保证为正数，必须满足．综合上面的讨论，要保证只有负数根，必须满足．评分参考：1讨论清楚有正数根的条件得4分；2讨论清楚有负数根的条件得4分；3给出正确结果得2分．12．答案：6解答：用A、B、C、D表示四种交通工具，分情况进行讨论．1如果去(或返回时，大家选择的工具没有相同的，则最多4位同学．2如果去(或返回时，恰有两位选择的工具相同，其他几位都与别人不同，则最多有5位同学．3如果去(或返回时，恰有三位选择的工具相同，其他几位都与别人不同，则最多有6位同学．4如果去(或返回时，有四位或更多选择的工具相同，则最多有4位同学．否则，假设有5位或更多同学．不妨设前四位选择了A，则他们返回(或去时选的工具一定互不相同，分别是A、B、C、D．返回(或去时，前四位之外的任何一位选择的工具一定与前四位中的某位相同．在这两位和前四位中的另外一位三人中，去(或返回时以及返回(或去时都至少有两位选择了相同交通工具．矛盾．上面的讨论说明，至多有6位同学．下表说明6位同学可以满足题设条件．1 2 3 4 5 6去 A A A B C D回 B C D A A A评分参考：1给出正确答案得2分；2说明6位同学可以得4分．3说明多于6人不可得4分．三、解答下列各题(每题l5分，共30分，要求写出详细过程13．解答：若被乘数“奇偶偶”<200，那么，偶奇偶偶=奇偶偶×偶<188×8=1504<偶奇偶偶．矛盾．所以，被乘数不小于300．被乘数的百位与乘数的十位的乘积应该小于8，否则加一个非0偶数就应该进位了，最后的结果应该是5位数，与竖式不符．所以，被乘数的百位是3，乘数的十位是2．因此：3偶偶×2=偶奇偶，被乘数的个位数只能6或8，否则不能进位；而被乘数的十位数只能是0，2或4，否则就要进位．因此，被乘数只可能是306，308，326，328，346，348．这些数乘以4或6都得不到“偶奇偶偶”，而348乘以8时，得“偶奇偶偶”，所以，最后得到右式．评分参考：1给出正确答案得8分；2给出理由得7分．14．答案：．解答1．如图1，连接AC．则三角形ACD的面积为，易知，，同法，连接BD，求得：……①如图2，连接EF，则ADFE是个梯形，设，则因为：，所以：……②即：．也就是：，所以：．即：．评分参考：1画出辅助线得2分；2讨论到①式得4分；3讨论到②式得6分；4得到正确答案得3分．解答2．如图3，记，，，．∵且，∴，∵，∴，求得：，∴．∴．。

-------------------------------------------------------装---------------------------------------------------------订--------------------------------------------------------------线------------------------------------------城市 学校 姓名 考号第十四届全国“华罗庚金杯”少年数学邀请赛第十四届全国“华罗庚金杯”少年数学邀请赛小 学 五 年 级 初 赛 试 卷（时间：2009年3月14日10：00～11：00）一、选择题（每小题10分，满分60分. 以下每题的四个选项中，仅有一个是正确的. 请将表示正确答案的英文字母写在每题的圆括号内）1．任意调换五位数54321的各个数位上的数字位置，所得的五位数中的质数的个数是（ ）.（A ）0个 （B ）1个 （C ）2个 （D ）3个2．2008年8月8日在北京举办第29届奥林匹克运动会，是星期五，那么一年后，即2009年8月8日是（ ）.（A ）星期四 （B ）星期五 （C ）星期六 （D ）星期日3．商店里有六箱货物，分别重15千克、16千克、18千克、19千克、20千克、31千克，两个顾客买走了其中五箱. 已知一个顾客买的货物重量是另一个顾客的2倍，那么，商店剩下的一箱货物重量是（ ）.（A ）20千克 （B ）19千克 （C ）18千克 （D ）16千克4．奥运会某国短跑队有12名运动员，其中3名起跑技术好，有4名跑弯道技术好，还有5人冲刺技术好. 现在要从中选4人组参加4×100米接力赛，为使每人充分发挥特长，共有（ ）种组队方式.（A ）12 （B ）60 （C ）240 （D ）1805．北京小学的五年级数学兴趣班里，男同学的人数比女同学的5倍少12人，比女同学的4倍多6人，教室里共有（ ）人.（A）94 （B）95 （C）96 （D）976．一家冷饮店规定在本店购买汽水喝完后，每三个空瓶可以换原装汽水一瓶.小张一行15人买了21瓶汽水，之后又用空瓶换汽水喝，没有一点浪费.这样他们一共喝了（）瓶汽水.（A）36 （B）45 （C）31 （D）21二、填空题（每小题10分，满分40分）7．五位棋手参赛，任意两人都赛过一局，胜一局得2分，败一局得0分，和一局得1分，按得分多少排名次.已知第一名没有下过和棋，第二名没有输过，第四名没有赢过.那么第一、第二、第三、第四、第五名的得分数分别是、、、、.8．在下面的算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字.如果“华＋庚＋金＋杯＋赛”＝30，那么“金杯赛”所代表的三位数是.9．有四个数，每次选取其中三个数，算出它们的平均数，再加上另外的一个数，用这样的方法计算了四次，分别得到以下四个数：22、25、34、39，那原来的四个数中最大的一个数是.10．如图，平行四边形ABCD的边长BC＝10厘米，直角三角形BCE的直角边EC＝8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，那么CF的长是厘米.第十四届华罗庚金杯少年数学邀请赛小学五年级初赛试题答案一、选择题（每小时10分，满分60分）题号 1 2 3 4 5 6答案 A C A D C C二、填空题（每小题10分，满分40分）题号7 8 9 10 答案6、5、4、3、2 965 28.5 5。

第一届华杯赛决赛一试试题1. 计算：2．975×935×972×（）,要使这个连乘积的最后四个数字都是“0”，在括号内最小应填什么数？3．把＋、－、×、÷分别填在适当的圆圈中，并在长方形中填上适当的整数，可以使下面的两个等式都成立，这时，长方形中的数是几？9○13○7=10014○2○5=□4．一条1米长的纸条，在距离一端0.618米的地方有一个红点，把纸条对折起来，在对准红点的地方涂上一个黄点然后打开纸条从红点的地方把纸条剪断，再把有黄点的一段对折起来，在对准黄点的地方剪一刀，使纸条断成三段，问四段纸条中最短的一段长度是多少米？5．从一个正方形木板锯下宽为米的一个木条以后，剩下的面积是平方米，问锯下的木条面积是多少平方米？6．一个数是5个2，3个3，2个5，1个7的连乘积。

这个数当然有许多约数是两位数，这些两位的约数中，最大的是几？7．修改31743的某一个数字，可以得到823的倍数，问修改后的这个数是几？8．蓄水池有甲、丙两条进水管，和乙、丁两条排水管，要灌满一池水，单开甲管需3小时，单开丙管需要5小时，要排光一池水，单开乙管需要4小时，单开丁管需要6小时，现在池内有池水，如果按甲、乙、丙、丁的顺序，循环各开水管，每天每管开一小时，问多少时间后水清苦始溢出水池？9．一小和二小有同样多的同学参加金杯赛，学校用汽车把学生送往考场，一小用的汽车，每车坐15人，二小用的汽车，每车坐13人，结果二小比一小要多派一辆汽车，后来每校各增加一个人参加竞赛，这样两校需要的汽车就一样多了，最后又决定每校再各增加一个人参加竞赛，二小又要比一小多派一辆汽车，问最后两校共有多少人参加竞赛？10．如下图，四个小三角形的顶点处有六个圆圈。

如果在这些圆圈中分别填上六个质数，它们的和是20，而且每个小三角形三个顶点上的数之和相等。

问这六个质数的积是多少？11．若干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一个盒子没有装棋子，然后他外出了，小光从每个有棋子的盒子里各拿一个棋子放在空盒内，再把盒子重新排了一下，小明回来仔细查看了一番，没有发现有人动过这些盒子和棋子，问共有多少个盒子？12．如右图，把1.2，3.7, 6.5, 2.9, 4.6，分别填在五个○内，再在每个□中填上和它相连的三个○中的数的平均值，再把三个□中的数的平均值填在△中，找出一个填法，使△中的数尽可能小，那么△中填的数是多少？13．如下图，甲、乙、丙是三个站，乙站到甲、丙两站的距离相等。

第十四届华罗庚金杯少年数学邀请赛初赛试卷（小学组）（时间：2009年3月14日 10：00～11：00）一、 选择题（每小题10分，满分60分. 以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内）第十四届华罗庚金杯少年数学邀请赛初赛10分1.下面的表情图片中，没有对称轴的个数为（ ）（A ） 3 (B ) 4 (C ) 5 (D ) 61.分析：通过观察可知，第1，2，5这三张图片是有对称轴的，其他的5张图片都没有对称轴，所以没有对称轴的个数为5，正确答案是C 。

第十四届华罗庚金杯少年数学邀请赛初赛10分2.开学前6天，小明还没做寒假数学作业，而小强已完成了60道题，开学时，两人都完成了数学作业. 在这6天中，小明做的题的数目是小强的3倍，他平均每天做（ ） 道题.（A ） 6 (B ) 9 (C ) 12 (D ) 152.分析：由于开学前6填时小强比小明多做了60道题，而开学时两人做的题一样多，所以这6填中小明比小强多做了60道题，而这6天中小明做的题的数目是小强的3倍，所以这6天小明做了60÷（3-1）×3=90道题，他平均每天做90÷6=15道题。

正确答案为D 。

第十四届华罗庚金杯少年数学邀请赛初赛10分3.按照中国篮球职业联赛组委会的规定，各队队员的号码可以选择的范围是0～55号，但选择两位数的号码时，每位数字均不能超过5. 那么，可供每支球队选择的号码共（ ）个 .（A ） 34 (B ) 35 (C ) 40 (D ) 563.分析：根据题意，可供选择的号码可以分为一位数和两位数两大类，其中一位数可以为0~9，有10种选择；两位数的十位可以为1~5，个位可以为0~5，根据乘法原理，两位数号码有5×6=30种选择。

所以可供选择的号码共有10+30=40种。

第十四届华罗庚金杯少年数学邀请赛初赛10分4.在19、197、2009这三个数中，质数的个数是（ ）.（A ） 0 (B ) 1 (C ) 2 (D ) 34.分析：19是常见的质数，197容易检验知也是质数，本题主要是考查2009这个数是否是质数。

华罗庚金杯少年数学邀请赛口试试题第01届华罗庚金杯少年数学邀请赛口试试题1. 这是七巧板拼成的正方形，正方形边长20厘米，问七巧板中平行四边形的一块（如右图中阴影部分）的面积是多少？2．从所有分母小于10的真分数中，找出一个最接近0.618的分数。

3．有49个小孩子，每人胸前有一个号码，号码从1到49各不相同，请你挑选出若干个小孩，排成一个圆圈，使任何相邻两个小孩的号码数的乘积小于100，你最多能挑选出多少个小孩子？4．有一路公共汽车，包括起点和终点站共有15个车站，如果有一辆车，除终点到站外，每一站上车的乘客中，恰好各有一位乘客从这一站到以后的每一站，为了使每位乘客都有座位，问这辆公共汽车最少要有多少个座位？5．正方形的树林每边长1000米，里面有白杨树和榆树，小明从树林的西南角走入树林，碰见一株白杨树就往正北走，碰见一株榆树就往正东走，最后他走了东北角上，问：小明一共走了多少米的距离？6．自然数按从小到大的顺序排成螺旋形，在2处拐第一个弯，在3处拐第二个弯，在5处拐第三个弯……问拐第二十个弯的地方是哪一个数？第02届华罗庚金杯少年数学邀请赛口试试题1、如下图是一个对称的图形，黑色部分面积大还是阴影部分面积大？2、你能不能将自然数1到9分别填入右面的方格中，使得每个横格中的三个数之和都是偶数？3、司机开车按顺序到五个车站接学生到学校（如下图），每个站都有学生上车，第一站上了一批学生，以后每站上车的人数都是前一站上车人数的一半，车到学校时，车上最少有多少学生？4、如图中五个正方形的边长分别是1米、2米、3米、4米、5米。

问：白色部分面积与阴影部分面积之比是多少？5、用1、2、3、4、5这五个数两两相乘，可以得到10个不同的乘积，问乘积中是偶数多还是奇数多？6、7、将右边的硬纸片沿虚线折起来，便可作成一个正方体，问：这个正方体的2号面对面是几号面？（如下图）8、下面是一个11位数，它的每三个相邻数之和都是20，你知道打“？”的数字是几？9、有八张卡片，右图分别写着自然数1到8，从中取出三张，要使这三张卡片上的数字之和为9，问有多少种不同的取法？第03届华罗庚金杯少年数学邀请赛团体决赛口试1．一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道红条，如右图阴影所示部分，红条宽都是2厘米．问：这条手帕白色部分的面积是多少？2．伸出你的左手，从大拇指开始如图所示的那样数数字，1，2，3，……，问：数到1991时，你数在那个手指上？3．有3个工厂共订300份吉林日报，每个工厂订了至少99份，至多101份．问：一共有多少种不同的订法？4．图上有两条垂直相交的直线段AB、CD，交点为E（如下图）．已知：DE=2CE，BE=3AE．在AB和CD上取3个点画一个三角形．问：怎样取这3个点，画出的三角形面积最大？5．如下图中有两个红色的圆，两个蓝色的圆，红色圆的直径分别是1992厘米和1949厘米，蓝色圆的直径分别是1990厘米和1951厘米．问：红色二圆面积大还是蓝色二圆面积大？6．在一张9行9列的方格纸上，把每个方格所在的行数和列数加起来（如下图），填在这个方格中，例如a=5＋3=8．问：填入的81个数字中，奇数多还是偶数多？7．能不能在下式：1□2□3□4□5□6□7□8□9=10的每个方框中，分别填入加号或减号，使等式成立？8．把一个时钟改装成一个玩具钟（如右图），使得时针每转一圈，分针转16圈，秒针转36圈．开始时3针重合．问：在时针旋转一周的过程中，3针重合了几次？（不计起始和终止的位置）．9．将1，2，3，4，5，6，7，8这8个数分成3组，分别计算各组数的和．已知这3个和互不相等，且最大的和是最小的和的2倍．问：最小的和是多少？10.这是一个棋盘，将一个白子和一个黑子放在棋盘线交叉点上，但不能在同一条棋盘线上．问：共有多少种不同的放法（如下图）？11.这是两个圆，它们的面积之和为1991平方厘米，小圆的周长是大圆周长的90％（如右图）．问：大圆的面积是多少？12.有一根1米长的木条，第一次去掉它的，第二次去掉余下木条的；第三次又去掉第二次余下木条的，等等；这样一直下去，最后一次去掉上次余下木条的．问：这根木条最后还剩下多长？13.这是一个楼梯的截面图（如下图），高2.8米，每级台阶的宽和高都是20厘米．问：此楼梯截面的面积是多少？14.请找出6个不同的自然数，分别填入6个括号中，使这个等式成立．第04届华罗庚金杯少年数学邀请赛团体决赛口试1．2×3×5×7×11×13×17这个算式中有七个数连乘，请回答：最后得到的乘积中，所有数位上的数字和是多少？请讲一讲你是怎样算的？2．这是一个中国象棋盘（图中小方格都是相等的正方形，“界河”的宽等于小正方形边长），黑方有一个“象”，它只能在1，2，3，4，5，6，7位置中的一个，红方有两个“相”，它们只能在8，9，10，11，12， 13，14中的两个位置．问：这三个棋子（一个“象”和两个“相”）各在什么位置时，以这三个棋子为顶点构成的三角形的面积最大？3．将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种形状的短管（加工损耗忽略不计）问：剩余部分的管子最少是多少厘米？4．乙两人同时从A出发向B行进，甲速度始终不变，乙在走前面路程时，速度为甲的2倍，而走后面路程时，速度是甲的，问甲、乙二人谁选到B？请你说明理由。

第十四届华罗庚金杯少年数学邀请赛决赛试题A （初一组）（时间：2009年4月11日10:00~11:30）一、填空题（每题10分，共80分）1．计算：()2414-3-6.5(2)(6)313⎛⎫-⨯+-÷-= ⎪⎝⎭949,解析：21041319416313269⎛⎫⎛⎫⎛⎫--⨯-+⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2．设有理数a,b,c 在数轴上的对应点如下图所示， 则代数式b a a c c b -+-+-=2（a-b ） 解析：()()()a>1 ;b<c<0;a-b ;=a-b =2a-b b a a c a c c b c bb a ac c b a c c b -=-=--=-∴-+-+-+-+-根据图像，得 则:;（）3．设m,n 是非负整数且3m<2n ，则三个n 次多项式之积与一个2m 次多项式之和是（3n ）次多项式 解析：24932 23,333m n m n m n n n n <→<<<=因为 且m>0,n>0,所以所以三个次多项式之积与一个2m 次多项式之和是 3n 次多项式4．一名运动员进行爬山训练，从山脚出发，上山路长10千米，每小时行3千米；爬到山顶后沿原路下山，下山每小时5千米，那么这位运动员上下山的平均速度是每小时（3.75）千米。

解析：依题意，列出算式 得101020=3.7535⎛⎫÷+ ⎪⎝⎭5．已知a,b 是有理数。

有以下三个不等式：①|a+b|<|a-b|,② a 2+b 2+|a|+|b|+1<0, ③a 2+b 2-2|a|-2|b|+1<0,其中一定不成立的是（②）（填写序号） 解析：22a 1 1.b a b ++++必定大于等于所以②必定不成立6．若二元一次方程组4234331x y n x y m -=-⎧⎨+=-⎩的解x,y 满足-1≤x ≤2,-2≤y ≤4,则m+n 的取值范围为：2.5m+n 10.5-≤≤解析：由4+3243+13x y n x y m -=⎧⎨+=⎩得123+9686+26x y n x y m -=⎧⎨+=⎩，两式相加：20x+3y+11=6(m+n),则因为-1≤x ≤2,-2≤y ≤4，有-15≤6(m+n)≤63，故-2.5≤m+n ≤10.57．把2006,2007,2008，2009四个数分别填入算式： 的四个方框中，则算式的最大可能值是：100331004解析：让被减数尽可能的最大，减数尽可能的小。

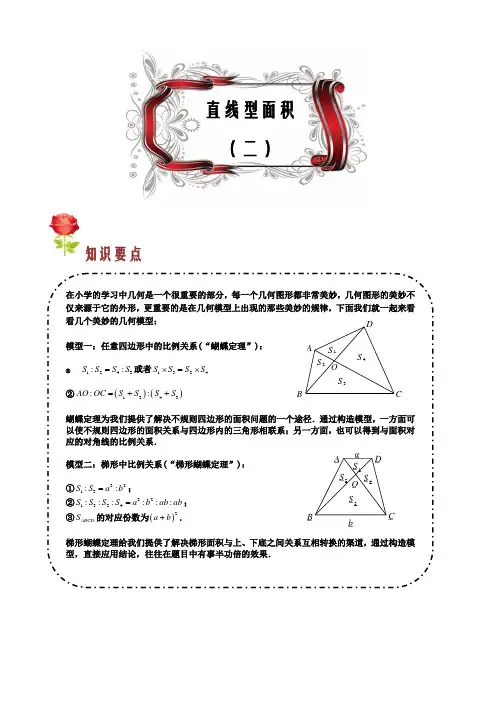
知识要点在小学的学习中几何是一个很重要的部分，每一个几何图形都非常美妙，几何图形的美妙不仅来源于它的外形，更重要的是在几何模型上出现的那些美妙的规律，下面我们就一起来看看几个美妙的几何模型：模型一：任意四边形中的比例关系(“蝴蝶定理”)：②1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系． 模型二：梯形中比例关系(“梯形蝴蝶定理”)：①2213::S S a b =；②221324::::::S S S S a b ab ab =；③ABCD S 的对应份数为()2a b +．梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道，通过构造模型，直接应用结论，往往在题目中有事半功倍的效果．直线型面积（二）S 4S 3S 2S 1O D C B A _ A _ B_ C_ D_ O _b_a_S _3 _S _2 _S _1 _S _4蝴蝶定理求面积【例1】 （小学奥林匹克）如图，已知梯形ABCD 的面积是45平方米，高6米，底边BC 长10米，三角形AED 的面积是5平方米。

求阴影部分的面积。

B CDE【分析】 根据梯形的面积公式，4526105AD =⨯÷-=（米）。

根据梯形蝴蝶定理，:1:4AED BEC S S =V V ，所以5420S =⨯=阴影（平方米）。

【例2】 如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：（1）三角形BGC的面积；（2）:AG GC =？A BDG321【分析】 ⑴根据蝴蝶定理，123BGC S ⨯=⨯V ，那么6BGC S =V ；⑵根据蝴蝶定理，()():12:361:3AG GC =++=．【例3】图中的四边形土地的总面积是52公顷，两条对角线把它分成了4个小三角形，其中2个小三角形的面积分别是6公顷和7公顷。