算法文字描述及流程图样例

开始
S←1，i←12
i←i－1
N
输出S
S←S×i
Y
结束
12．以下给出的是计算1/2＋1/4＋1/6＋…＋1/20的值的一个流程图， 判断框内应填入的条件为___．
开始 S←0，n←2，i←1
i←i＋1 n←n＋2 S←S＋1/n
N Y 输出S 结束
13．下图流程图是计算1＋1/3＋1/5＋…＋1/99的流程图，请你补充完整． 开始
开始 x ← 1，S ← 0
x≤5 Nቤተ መጻሕፍቲ ባይዱ输出S
x←x＋1 S←S＋x2 Y
结束
5．如图所示的流程图输出的第2013个数为_1_0__0_7___．
开始 A←1，N←1
输出A N←N＋1
N≤5000 N 结束
A←A＋1/2 Y
6．下图所示流程图输入n＝7，输出的结果为 13 ．
开始 输入n A←1，B←1，K←3
2．执行如图所示的流程图，则输出S＝_5_0__5_0__．
开始 S←1 I←2
I ← I＋1 S ← S＋I
I ≤100
Y
N
输出S
结束
3．下图所示的流程图的输出结果为2_5__6_． 开始 p←0
i←1
p ← p＋i
i ← i＋2
i＞31
N
Y
输出p
结束
4．下图所示的流程图的输出结果为_5_5__．
开始 i←1，m←0，T←0
输入x x＞80 N
Y 输出x
T←T＋x m←m＋1
i←i＋1
N
i＞15
Y
P←T/m
输出P 结束
9．如下流程图，循环体执行的次数为 （ ）
开始

输入、输出框: 作用：指出要输入和输出的内容。 例如：
输入a
特点：一个入口 和 一个出口
处理框:
作用：指出要处理的内容。 例如：
a=a+1
a=a+1
???
特点：一个入口 和 一个出口
判别框:
作用：用于表示分支情况，框内书写判断条件。 例如：
Y N
a≤b
特点：一个入口 和 两个出口
流程线:
作用：用于表示程序的流向。 例如：
Y N
a≤b
连接框:
作用：用于连接因写不下而断开的流程线。 例如：
1 1
特点：一个入口 或 一个出口
练一练
用流程图描述用高斯公式求自然数 之和的算法。 sum = 1 + 2 + 3 + … + (n-1) + n
自然语言
1.输入n的值 1+n 2.计算 sum = ×n 2 3.输出sum的值
N
输出sum
End
用流程图描述算法 T = n! = 1×2×3×…×n
自然语言 1. 2. 3. 4. 5. 6. 输入n; sum=1; i=1; 计算sum=sum*i; 计算i=i+1; 如果i≤n执行4， 否则执行7 7. 输出sum的值 并结束算法。
流程图
Start
输入n
sum=1,i=1 sum=sum*i i=i+1 Y i≤n
算法和算法描述的方法农夫带狼、山羊、蔬菜过河的问题
一个农夫带着一条狼、一头山羊和一
篮蔬菜过河，但只有一条小船。每次只能
让农夫带一样东西过河，而且农夫在场的 情况下三样东西将相安无事。一旦农夫不 在，狼会吃羊，羊会吃蔬菜。问农夫如何 能安全地带这三样东西过河？

任务1 某学生五门功课成绩为 、 、 、 、 任务1：某学生五门功课成绩为80、95、78、87、 65.写出求平均成绩的算法，并画出流程图 写出求平均成绩的算法， 写出求平均成绩的算法 并画出流程图.
程序框图： 程序框图： 解：算法步骤为： 算法步骤为： 第一步，80、95、78、87、 第一步， 、 、 、 、 65. 第二步，计算 第二步，计算p=
算法3：（ 算法 ：（1+99）+（2+98）+（3+97）+…（49+51） ：（ ） （ ） （ ） （ ） +50+100=5050
第三部分 温故知新
尝试分析右侧流 程图的数学表达 式.
开始 输入x 输入 x≥0? 是 输出y=x 输出 否 输出y=1-x 输出
结束
3、课堂练习
• 用流程图描述算法。
80+95+78+87+65 5
输入80、 、 、 、 输入 、95、78、87、65
开始
p=80 +95+ 78+87 + 65
5
输出p 输出
第三步， 第三步，输出 p .
结束
任务2 写出下列流程图的运行结果： 任务2：写出下列流程图的运行结果：
开始 输入a， 输入 ，b a＝2 ＝ b＝ b＝4
第一部分 复习引入
1.算法的含义是什么？ 1.算法的含义是什么？ 算法的含义是什么 解决问题的方法和步骤称为算法. 解决问题的方法和步骤称为算法. 2.分析作业问题并呈现学生的算法 分析作业问题并呈现学生的算法
人+2虎 虎
一个人带三只老虎和三头牛 过河。只有一条船， 过河。只有一条船，同船可 以容一个人和两只动物。 以容一个人和两只动物。没 有人在的时候， 有人在的时候，如果老虎的 数量不少于牛的数量就会吃 掉牛。设计安全渡河的算法。 掉牛。设计安全渡河的算法

输出sum 用N-S图表示
N i<n?
Y t*=i;sum+=t;
iቤተ መጻሕፍቲ ባይዱ=2 输出sum
结束 用流程图表示
8.7 跟我上机
2. 将1到100之间 能用3或5整 除的数打印 出来。
开始
i赋初值为1
N i<=100?
Y N
i能被3或5整 除？ Y 打印i
i++
结束
用流程图表示
i赋初值为1
i<=100?
i能被3或5整 除？
N d>=0？
x2=x-sqrt(-d)/(2a) x1=x+ sqrt(-d)/(2a)
输出结果
8.7 跟我上机
开始 输入n的值
1. 求1！+3！+5！+……+N!的值。N
i赋值为1 t赋初值为1
由键盘输入，且为奇数。
sum赋初值为0
输入n的值 t赋初值为1； i赋值为1
sum赋初值为0 i<n? t*=I; s+=t; i+=2
求最大公约数通常用“辗转相除法”，
方法如下：
（1）比较两数，并使m大于n。 （2）将m作被除数，n作除数，相除 后余数为r。 （3）将m←n，n←r； （4）若r=0，则m为最大公约数，结 束循环。若r≠0，执行步骤步骤（2） 和（3）。
输入m,n
T
m<n?
F
交换m,n
r←m%n m←n，n←r
r ≠0 输出m
8.3.6 用计算机语言表示算法
计算机语言通常分为三类：即机器语言，汇编语 言和高级语言。
8.4 结构化程序设计方法
结构化程序设计的思想：自顶向下、逐步求 精；

程序框图的发展趋势
可视化编程
随着可视化技术的发展，程序框 图成为一种直观的编程方式。通 过图形化的方式描述程序逻辑， 降低了编程难度，提高了开发效 率。
交互式编程
交互式编程让用户在编程过程中 能够实时查看程序运行结果，及 时调整代码。这种编程方式提高 了开发效率和程序质量。
智能生成与自动优
化
基于机器学习和人工智能技术， 程序框图可以自动生成和优化程 序代码。这大大减少了编程工作 量，提高了开发效率。
算法的复杂度分析
随着计算机科学的发展，算法的复杂度分析越来越受到重 视。人们不断探索更高效的算法，以提高计算效率和准确 性。
机器学习与人工智能算法
随着人工智能的兴起，机器学习与人工智能算法成为研究 热点。这些算法能够从大量数据中自动提取有用的信息， 为决策提供支持。
并行计算与分布式算法
为了处理大规模数据和复杂问题，并行计算和分布式算法 成为研究重点。这些算法能够充分利用多核处理器和分布 式系统的优势，提高计算性能。
算法的表示方法
01
自然语言描述
用简洁明了的文字描述算法的步骤。
流程图
用图形符号表示算法的步骤和流程。
03
02
伪代码
用类似于编程语言的简化和结构化 形式描述算法。
程序代码
用编程语言实现算法的具体代码。
04
算法的复杂度分析
时间复杂度
评估算法执行时间随输入规 模增长的情况，表示为 O(f(n))。
空间复杂度
选择结构是根据条件判断选择不同的执行路径的程序框图 结构。它使用判断框来表示条件判断，根据条件的结果选 择不同的执行路径。选择结构可以有效地处理具有多个分 支的情况，提高程序的灵活性和适应性。

项目：请同学们结合自身疫情防控的经验， 绘制一份寄宿制学校疫情防控期间复学入校的流程图。
项目一：
绘制复学入校这一问题的流程图。
项目一：复学入校这一问题的流程图。
项目二：
如果测温超过37.2，那么由校医带至隔离室等待家长接回， 并对隔离室进行消毒。
绘制流程图，解决体温 异常无法入校的处理方 式。
项目总结：
算法及流程图表示
算法及流程图表示
信息技术 高一 浙教版《数据与计算》2.1.2
第一步 把冰箱门打开 第二步 把大象放进去 第三步 把冰箱门关上。
一、算法的概念
算法就是解决问题的方法和步骤。
二、算法的表示
用自然语 言描述算
法。
算法 表示
用流程 图描述 算法。
用伪代 码描述 算法。
流程图图形符号表
二、算法的表示——流程图
项目二：如果测温超过37.2，那么由校医带至隔离室等 待家长接回，并对隔离室进行消毒。பைடு நூலகம்
绘制流程图，解决体 温异常无法入校的处 理方式。
项目三： 完成全年级共500名学生的入校流程。
绘制流程图，解决500名 学生复学入校这个问题
项目三：全年级共500名学生的入校流程图
绘制流程图，解决500名 学生复学入校这个问题

1 1 1 1 求 的值. 3 5 7 19
；算法Ⅱ的
算法Ⅰ：
算法Ⅱ ：
二、解答题 10.（2010·江苏南京模拟）已知f（x） =x2-2x-3,求f（3）、f（-5）、f（5）, 并计算f（3）+f（-5）+f（5）的值. 设计出解决该问题的一个算法， 并画出流程图. 解 算法如下： S1 x←3; S2 y1←x2-2x-3; S3 x←-5; S4 y2←x2-2x-3; S5 x←5; S6 y3←x2-2x-3; S7 y←y1+y2+y3; S8 输出y1,y2,y3,y. 该算法对应的流程图如右图所示.
［4分］
［8分］
伪代码如下：
［14分］
跟踪练习4 解
编写一组伪代码计算 1 1 1 1 2 3 1 000 的值，并画出相应的流程图. 伪代码如下
流程图如图所示：
思想方法 感悟提高
高考动态展望
高考中常以填空题的形式考查流程图、条件语句、
循环语句等的简单应用，属中档题.
方法规律总结
4.下列4种框图结构中，是直到型循环结构的为 ② （填序号）.
解析
根据直到型循环结构的特点，可知“当条
件不满足时执行循环体，满足时退出循环体”， 也就是先执行后判断，所以只有②符合，故填②. 其中①是当型循环结构，它是先判断后执行.
典型例题
深度剖析
【例1】已知点P（x0，y0）和直线l:Ax+By+C=0， 求点P（x0，y0）到直线l的距离d，写出其算法 并画出流程图. 分析 利用点到直线的距离公式可写出算法， 而流程图利用顺序结构比较简单. 解 算法如下：
1 ( x 0) 跟踪练习2 函数 y 0 ( x 0) , 写出求该函数 1 ( x 0) 值的算法并出画流程图.

筑物 环境制作和灯
光设计
结束
画流程图
例1.输入圆半径，计算圆面积并输出
开始 输入半径r
面积=πr^2
输出面积
结束
练习3.用流程图描述以下算法： （见练习）
1.输入两个自然数A、B，计算两数之和， 输出结果。
2 画流程图
例2.输入两个数A，B，输出较小者
练习2.用流程图描述以下算法： （见练习）
2.输入一个学生成绩A，良好，小于60分输出不合格。
(一）自然语言 用自然语言描述以下算法
（见练习） 1.取款机提现金(取款机前） 2.医院看病 3.有二杯水，A杯盐水，B杯
糖水，请将 它们互换后A杯为糖 水，B杯为盐水可以借助C容器
这节课你学了什么？
作业：继续完成随堂练习
第二课算法及流程图
缙云新建中学 孙 玲
一、算法的概念
就是解决某一个实际问题所 采用的方法和步骤
二、算法的表示
自然语言 流程图 计算机程序代码等
（二）流程图——认识流程图
开始，结束框 处理框（1入1出） 输入，输出框（1入1出） 判断，选择框（1入2出）
流程线框
建筑模型制作流程图
开始
设计图纸 机器雕刻 工人手工制作建

使⽤流程图表⽰算法⼀、传统流程图
流程图表⽰算法，直观形象，易于理解。

1、常⽤流程图说明：
2、三种基本结构和改进的流程图
顺序结构：
选择结构：
循环结构：
三种基本结构的共同特点：
只有⼀个⼊⼝；
只有⼀个出⼝；
结构内的每⼀部分都有机会被执⾏到；
结构内不存在“死循环”。

3、制作流程图步骤
创建流程图：根据要表达的活动，选择流程图标准符号中的图例。

移动和调整形状⼤⼩：
添加修改⽂本
连接图例
4、⽰例
⽰例1：求5!的算⽤流程图表⽰。

⽰例2：判定闰年的算⽤流程图表⽰
⼆、⽤N-S流程图表⽰算法
1973年美国学者提出了⼀种新型流程图：N-S流程图。

顺序结构：
选择结构：
循环结构：
⽰例1：求5!的算⽤流程图表⽰。

⽰例2：判别素数的算⽤流程图表⽰。

程线 处理框
输入/输出框 判断框
含义
流程的开始或结束 流程的走向 对数据的处理
数据的输入或输出 根据条件判断
小试牛刀
计算长方形的周长，已知长8米，宽4米
步骤一：计算8+4的值为12 步骤二：计算12 × 2的值为24 步骤三：输出算式的值24
计算12*2的值
计算8+4的值
忆一忆
同学A和同学B换座位，用自然语言怎么描述步骤？
步骤1：把A桌子移到空地。 步骤2：把B桌子移到原来A 桌子的位置。 步骤3：把A桌子移到原来B 桌子的位置。 步骤4：两张桌子前后对齐， 完成交换。
流程图 描述算法
浙摄版2023
概念
流程图以图示的方法来描述算 法，具有形象直观、结构清晰、 逻辑性强等特点
输出 长方形周长的值
注意流程图的顺序： 从左到右、从上到下，
不能交叉或者弯曲
练一练：圆的面积为12.56m2,那么该圆的周长是多少？
步骤1:
步骤2:
流
程
步骤3:
图
怎么把纸质上的流程图搬到计算机中？
画图、Word等
完成下发的练习
感谢聆听
侵删

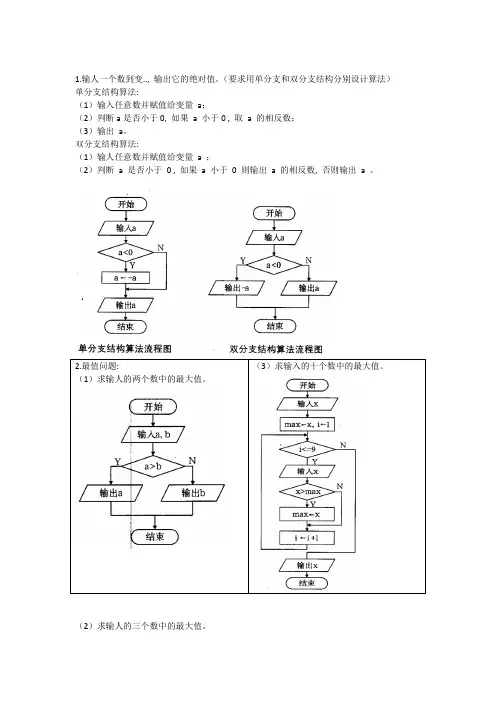
1.输人一个数到变.., 输出它的绝对值。

（要求用单分支和双分支结构分别设计算法）单分支结构算法:
（1）输入任意数并赋值给变量a；
（2）判断a是否小于0, 如果a 小于0 , 取a 的相反数；
（3）输出a。

双分支结构算法:
（1）输人任意数并赋值给变量 a ；
（2）判断a 是否小于0 , 如果a 小于0 则输出a 的相反数, 否则输出a 。

（3）求输入的十个数中的最大值。

2.最值问题:
（1）求输人的两个数中的最大值。

（2）求输人的三个数中的最大值。

3.循环求和（不同的控制循环方法）
1.求输.
2.个数的和。

(知道循环次数, 可以采用循环变量i 来控制循环次数)
计数法2.求输入的若干个学生成绩
的和, 输.-1表示结束。

（不能确定次数, 可以用输
入的数据的值来进行控制）
标志法
3.对输入的数据求和, 当所求
的和超.10.则停止输入并输出
求和结果（设此题中输人的数
皆为正数）。

（没有指出输人数据的具体个
数, 且不能依据对输入数据的
值来控制循环, 控制循环的关
键就在于对循环体中变量s
的判断）
（没有指出输人数据的具体个
数，且不能依据对输入数据的
值来控制循环，控制循环的关
键就在于对循环体中变量s
的判断）
输出如下图形:
**********
**********
**********
**********
**********
如下算法能输出哪种图形？（A）。

i<５? 否 是 i←i+1 Sum ← Sum + i
输出Sum 结束
开始
i ← 0，Sum ← 0
i←i+1
Sum ← Sum + i
否
i≥５?
是 输出Sum
结束
循环结构：在一些算法中，也经常会出现从某处开始，按照一定条 件，反复执行某一处理步骤的情况，这种结构称为循环结构.
循环体：反复执行的处理步骤称为循环体. 计数变量：在循环结构中，通常都有一个起到循环计数 作用的变量，这个变量的取值一般都含在执行或终止循 环体的条件中. 当型循环：在每次执行循环体前对控制循环条件进行判 断，当条件满足时执行循环体，不满足则停止. 直到型循环：在执行了一次循环体之后，对控制循环体 进行判断，当条件不满足时执行循环体，满足则停止.
流程图
i) 顺序结构
三种基本算法结构
ii) 选择结构
Yp N A
A
B
B
循环结构
算法2流程图:
算法2: S1 T←1； S2 S←2； S3 T←T×S； S4 S←S+1； S5 如果S不大于5,返
回 S3,否则输出T。
开始 T←1 S←2 T←T×S S←S+1
S>5 Y
N
输出T
结束
开始 i←0，Sum ← 0
n 6, m 4那么输出的
p 等于（ ） A.720 B.360 C.240 D.120
x 10
x4
开始
A=1，B=1
A≤5？ 否 输出B
A=A+1
B=2B+1 是
结束缚
开始
Sum←0,i←1
Sum←Sum+1

算法流程图：
开始
输入a,b
Y a<b?
N
输出a,b
输出b,a
结束
用流程图来描述下列问题的算法：
例3：求：1+2+3+……+n的和。（n由键 盘输入的自然数）
算法流程图：
开始 输入n
i=1
Sum=0 N
i<=n? Y
Sum=sum+i
i=i+1
输出sum 结束
用流程图描述下列问题的算法： 1、输入一个数,要求输出这个数的相反数。
用流程图描述下列问题的算法：
2、有一函数：输入一个x值，输出相应的y值。 -1 (x<0)
Y= 0 (x=0) 1 (x>0)
3.用伪代码描述算法
---------将编程语言和自然语言巧妙结合起来的一种 描述算法的方法。
例：有一函数：输入一个x值，输出y值。
-1 (x<0) 伪代码表示如下：（类pascal)
作业：用流程图描述下列问题的算法
1、输入一个数，输出该数的平方和立方值。 2、输入一个数，输出它的算术平方根。 3、输入三个数，判断这三个数构成的线段能
否组成一个三角形，若能输出“可以！”， 否则输出“不行！”。
算法的三种描述方法
1、自然语言 2、流程图 3、伪代码（或程序）
1.用自然语言描述算法
例：输入两个数，输出它们的和与差。
算法： 步骤1：输入两个数a,b 步骤2：计算s1=a+b 步骤3：计算s2=a-b 步骤4：输出s1,s2，结束。
2.用流程图描述算法
--------用图形来描述算法的方法。
处理框
输入输出框
判断框

算法流程图(循环结 构)
目录
• 循环结构的概述 • 循环流程图的绘制 • 常见的循环结构算法 • 循环结构的应用场景 • 循环结构的注意事项 • 案例分析
01
循环结构的概述
循环结构的定义
循环结构是算法流程图中的一种基本结构，用于 01 重复执行一段代码，直到满足某个条件为止。
循环结构由三个基本部分组成：初始化、循环体 02 和终止条件。
详细描述
在for循环中，首先定义一个计数器变量和循环次数，然后在每次循 环中执行指定的操作，直到计数器达到设定的循环次数为止。
示例
以下是一个简单的for循环算法，用于计算1到10的累加和
for循环算法
```
sum = sum + i
for i = 1 to 10 do
for循环算法
end for ```
VS
详细描述
for循环通常用于已知循环次数的情况， 它包含三个基本部分：初始化、条件和后 续操作。在流程图中，for循环通常以矩 形表示，并在其中标明循环变量、初始值 、条件表达式和增量。例如，计算1到10 的累加和可以使用以下for循环实现
for循环的案例分析
```
for (int i = 1; i <= 10; i) {
控制条件的绘制
01 绘制一个菱形，标注为“条件”，表示循环的控
制条件。
02
在条件菱形内标注判断的具体内容，如“i<10” 。
循环次数的表示
使用一个数字标注在控制条件旁边，表示循环的 次数。
如果循环次数是动态变化的，可以使用变量代替 数字，如“n”。
03
常见的循环结构算法
for循环算法
总结词
for循环是一种预先设定循环次数的循环结构，通常用于已知循环次 数的情况。

算法名称：求最大值算法输入：输入10个数算法输出：最大值算法描述：step1:输入astep2:n=1，m=astep3:当n＜=10时：输入an=n+1若m＜a成立，则m=a step4:输出mRaptor流程图及结果截图算法名称：求数的平均值算法输入：无算法输出：平均值算法描述：step1:s=0;num=0step2: n=200step3:当n<=300时：若n%3=0 or n%7=0成立S=s+nNum=num+1N=n+1step4:ave=s/numstep5:输出aveRaptor流程图及结果截图算法名称：计算公式前n项之和算法输入：n算法输出：前n项之和算法步骤：step1：输入nstep2.1：将1赋值给x2.2将0赋值给s2.3将s+1/x赋值给s2.4将x+1赋值给x2.5判断x>n?2.5.1为真，转32.5.2为假，转2.3step3:输出sRaptor流程图及结果截图：算法名称：求满足条件的所有的数算法输入：300-500之间的数算法输出：满足条件的所有的数算法步骤：Step1:将300赋值给xStep2.1百位a=floor（x/100）2.2十位b=floor（x/10）2.3个位c=x mod 102.4判断a*b*c=42 or a+b+c=5?2.4.1为真，输出x2.5将x+1赋值给x2.6判断x>500?2.6.1为真，转32.6.2为假，转2.1step3：结束Raptor流程图及结果截图：算法名称：计算大人数和幼儿数算法输入：无算法输出：大人数和幼儿数算法描述：step1:x=1step2: 当x<25时若4x+（100-x）/4=100成立输出大人数x输出幼儿数100-xstep3:x=x+1step4: 当x<25时若4x+（100-x）/4=100成立输出大人数x输出幼儿数100-x Raptor流程图及结果截图。

一、算法的概念
算法（algorithm）这个词出现于12世纪，指的是用阿拉伯数字进行运算的过程。

在数学中，现代意义上的“算法”通常是指可以有计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成。

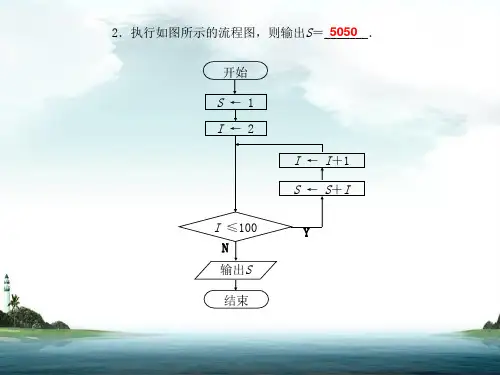
例3、求1+2+3+···+100的和。

算法分析：
第一步：对称地取前后两数相加，即1+100，2+99，
3+98，···，50+51，得出两数之和都是101的规律。

第二步：这样的和式共有100/2个，即50个
第三步：总结出计算方法：101*100/2
第四步：计算上式得出结果5050。

方法二：直接累加求1+2+3+ ···+100的和，虽然也能求得结果，但是要做99次加法，这显然是十分烦琐的。

如何去设计算法呢？设计的算法又怎么表示呢？大家看到了，算法的设计分两个内容：一是寻找一种方法；二是描述一下实现这个方法的步骤。

刚才我们已经用语言的形式描述过算法了。

我们还可以用流程图的方法来描术算法。

流程图，又叫做程序框图，是一种较常用的算法表示方法。

流程图用一些几何图形符号表示各种类型的操作，并在框内以简明文字或符号表示具体操作。

实数根的算法（如下图）
用程序框图来表示算法，算法的基本逻辑结构展现得非常清楚，一共有三种不同的基本逻辑结构，分别称为顺序结构、条件结构和循环结构。

顺序结构：完全按照框图的排列顺序执行的结构。

如下图：
例4、用流程图描述求一元二次方程： )0(02
≠=++a c bx ax。

程序算法描述流程图程序算法流程图算法的方法递推法递推是序列计算机中的一种常用算法。

它是按照一定的规律来计算序列中的每个项，通常是通过计算机前面的一些项来得出序列中的指定项的值。

其是把一个复杂的庞大的计算过程转化为简单过程的多次重复，该算法利用了计算机速度快和不知疲倦的机器特点。

递归法程序调用自身的编程技巧称为递归(recurion)。

一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

递归的能力在于用有限的语句来定义对象的无限集合。

一般来说，递归需要有边界条件、递归前进段和递归返回段。

当边界条件不满足时，递归前进;当边界条件满足时，递归返回。

注意：(1)递归就是在过程或函数里调用自身;(2)在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。

穷举法穷举法，或称为暴力破解法，其基本思路是：对于要解决的问题，列举出它的所有可能的情况，逐个判断有哪些是符合问题所要求的条件，从而得到问题的解。

它也常用于对于密码的破译，即将密码进行逐个推算直到找出真正的密码为止。

例如一个已知是四位并且全部由数字组成的密码，其可能共有10000种组合，因此最多尝试10000次就能找到正确的密码。

理论上利用这种方法可以破解任何一种密码，问题只在于如何缩短试误时间。

因此有些人运用计算机来增加效率，有些人辅以字典来缩小密码组合的范围。

贪心算法贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。

用贪心法设计算法的特点是一步一步地进行，常以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，它省去了为找最优解要穷尽所有可能而必须耗费的大量时间，它采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解，虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪婪法不要回溯。