p99-图乘法的公式和适用条件.

人教版小学阶段《乘法》思维导图一、乘法的概念1. 乘法的定义：乘法是一种基本的数学运算，表示将两个或多个数相乘的运算。

2. 乘法的符号：乘法运算使用符号“×”或“·”表示。

3. 乘法的意义：乘法可以理解为重复加法的简化形式。

例如，3×4可以理解为将3加上自己4次，即3+3+3+3。

二、乘法的性质1. 交换律：乘法满足交换律，即a×b=b×a。

例如，2×3=3×2。

2. 结合律：乘法满足结合律，即(a×b)×c=a×(b×c)。

例如，(2×3)×4=2×(3×4)。

3. 分配律：乘法满足分配律，即a×(b+c)=a×b+a×c。

例如，2×(3+4)=2×3+2×4。

三、乘法的应用1. 计算面积：乘法可以用来计算矩形的面积。

例如，长为5厘米，宽为3厘米的矩形，其面积为5×3=15平方厘米。

2. 计算总数量：乘法可以用来计算多个相同物品的总数量。

例如，每个书包的价格为10元，购买3个书包的总价为10×3=30元。

3. 解决实际问题：乘法在解决实际问题中具有广泛的应用。

例如，计算汽车的行驶距离、计算人数、计算时间等。

四、乘法的扩展1. 乘法的扩展：乘法可以扩展到多个数的乘积。

例如，3×4×5表示将3、4、5相乘，即3×4×5=60。

2. 乘法的扩展应用：乘法的扩展可以应用于更复杂的数学问题，如分数乘法、小数乘法等。

人教版小学阶段《乘法》思维导图一、乘法的概念1. 乘法的定义：乘法是一种基本的数学运算，表示将两个或多个数相乘的运算。

2. 乘法的符号：乘法运算使用符号“×”或“·”表示。

3. 乘法的意义：乘法可以理解为重复加法的简化形式。

p99计算方法摘要：1.计算方法概述2.P99计算方法的原理3.P99计算方法的步骤4.应用场景及案例分析5.注意事项及实用技巧正文：【1】计算方法概述在众多计算方法中，P99计算方法是一种常用于评估产品性能、服务质量以及用户满意度的重要指标。

P99，又称百分位数，是指在数据集中大于或等于99%的数据值。

换句话说，P99表示在所有数据中排名前1%的数值。

在实际应用中，P99可以帮助企业或组织更好地了解产品的性能上限，从而为改进产品和服务提供依据。

【2】P99计算方法的原理P99计算方法的原理是基于统计学原理，对数据进行排序和分组。

具体来说，首先将数据集按照大小顺序进行排列，然后计算排名前1%的数据值所占比例的累积百分比。

这个累积百分比对应的数值即为P99。

【3】P99计算方法的步骤计算P99的方法相对简单，可以分为以下几个步骤：1.收集数据：首先需要收集与评估指标相关的数据，如产品性能、服务质量等。

2.数据排序：将收集到的数据按照大小顺序进行排序，形成一个数据列表。

3.确定百分位数：根据排序后的数据，计算出排名前1%的数据值所占比例的累积百分比。

4.计算P99：找到累积百分比对应的数值，即为P99。

【4】应用场景及案例分析P99计算方法在以下场景中具有广泛的应用：1.产品质量评估：企业可以利用P99来衡量产品的性能指标，如响应时间、处理能力等，从而找出产品的瓶颈并进行优化。

2.服务质量评估：在服务业，P99可以用于评估客户满意度、投诉率等指标，以便提高服务质量。

3.供应链管理：P99可用于评估供应商的质量水平，帮助企业优化供应链。

【5】注意事项及实用技巧在进行P99计算时，应注意以下几点：1.数据完整性：确保收集的数据完整，避免遗漏。

2.数据准确性：对收集的数据进行核实，确保数据准确无误。

3.考虑数据分布：若数据分布不均匀，可采用其他百分位数（如P75、P90等）作为补充评估指标。

4.结合其他指标：P99计算方法并非万能，还需结合其他指标（如平均值、标准差等）进行全面评估。

1.2.3图乘法图乘法是关于的简化计算方法。

在一定的应用条件下，图乘法可给出该积分的数值解，而且是精确解。

适用条件（1）杆件为直杆；（2）EI为常数（等截面）；（3）和图中至少应有一个直线图形。

对于等截面直杆所构成的梁和刚架，都能同时满足以上三个条件，因而均可采用弯矩图图乘的方法，简称图乘法。

算位移的公式（1-15）式中为、图中某一图形的面积；为与该截面形心对应的另一个图形的竖标。

这样，就将较为复杂的积分运算问题简化为求图形的面积、形心和标距等几何运算问题。

三）几种常见图形的面积的形心位置在图1-15中，给出了位移计算中几种常见图形的面积公式和形心位置。

图1-15【注意】在所示的各次抛物线图形中，抛物线“顶点”处的切线都是与基线平行的。

这种图形可称为抛物线标准图形。

应用图中有关公式时，应注意这个特点。

（四）图乘法计算位移必须注意的几个问题（1）必须取自直线图形。

（2）与若在杆件同侧时，其乘积取正号；反之，取负号。

（3）如果两个图形都是直线图形，则可取自其中任何一个图形。

（4）如果图是曲线图形，图是折线图形，则应分段互乘，最后叠加。

（5）如果图形比较复杂（由不同类型的多个荷载作用绘出），其面积和形心位置不便确定时，则可利用“区段叠加法”的逆运算，将其分解为几个简单的标准图形，并将它们分别与另一个图形图乘，最后叠加。

（6）如果杆件EI分段变化时，可分段图乘，最后叠加。

（7）如果EI沿杆长连续变化或是曲杆和拱结构，则必须用积分计算位移。

（1）绘实际荷载作用下的图；（2）根据所求位移，加相应单位力，绘图；（3）代入式（1-15）求位移：【注意】根据计算结果的正负号，判定位移的实际方向，并在计算值之后所加的圆括号中，标明其实际方向。

图乘法原理
图乘法原理是指在进行图的乘法运算时，将两个图的每个顶点对都连接起来，形成一个新的图。

这个新图的顶点由两个原始图的顶点组成，边由两个原始图的边组成。

具体而言，设图G1=(V1,E1)和图G2=(V2,E2)是两个图，其中
V1和V2分别是G1和G2的顶点集合，E1和E2分别是G1和G2的边集合。

那么图乘法原理定义了一个新的图G=(V,E)，
其中V=V1×V2，即G的顶点是由G1和G2的顶点对组成的。

而E是由所有G1和G2的边连接起来的，即对于每个
(u,v)∈V1×V2，如果存在(u1,v1)∈E1和(u2,v2)∈E2满足u=u1，v=v2，那么(u,v)∈E。

通过图乘法原理，我们可以将两个图的结构进行组合，得到一个新的图。

这个新图中的顶点保留了原来两个图的顶点的属性，而边则是两个图的边的组合。

在实际应用中，图乘法原理可以用于表示两个图之间的关系，例如社交网络中的用户之间的关注关系和互动关系等。

总之，图乘法原理是一种用于将两个图进行乘法运算的方法，通过将两个图的顶点对连接起来，形成一个新的图。

它可以用于表示两个图之间的关系，在图论和网络分析领域有着广泛的应用。

九九乘法表知识点九九乘法表是数学中非常重要的基础知识之一，通过学习九九乘法表，我们能够深入理解乘法运算的特性，提高计算能力以及解决实际问题的能力。

在本文中，我们将探讨九九乘法表的相关知识点。

1. 乘法运算的定义乘法是基本的四则运算之一，在乘法运算中，我们将两个数相乘，结果称为乘积。

九九乘法表中的每个数都是由两个自然数相乘得到的乘积。

2. 九九乘法表的规律九九乘法表具有一定的规律性，掌握了这些规律，我们就能够快速准确地计算出九九乘法表中的任意乘积。

首先，九九乘法表中的每一行和每一列的第一个数都是1，即1×1=1，1×2=2，1×3=3，依此类推。

其次，每一列中的数是随着行数的递增而递增的，即第二列中的数为2，3，4...，第三列为3，4，5...，以此类推。

另外，九九乘法表中的对角线上的数具有特殊性质。

对角线上的数都相等，即第一行第一列的数是1，第二行第二列的数是4，第三行第三列的数是9...，这是由于两个相等的数相乘得到的结果也相等。

3. 九九乘法表的应用九九乘法表在日常生活和学习中有广泛的应用。

首先，它为我们提供了数字之间相乘的基础概念，是后续数学学习的基石。

其次，九九乘法表可以帮助我们进行简单而准确的计算，如快速算出两个数的乘积、计算商品的价格等。

此外，在解决实际问题时，九九乘法表也能够发挥重要作用，如计算面积、体积等。

4. 学习九九乘法表的方法为了更好地掌握九九乘法表，我们可以采用以下几种学习方法：（1）背诵法：通过不断背诵九九乘法表，我们可以加深对乘法结果的记忆，提高计算速度和准确度。

（2）图形法：可以通过画九九乘法表的形式来进行学习，将每个乘积用格子或点的形式表示出来，通过观察图形来记忆和理解乘法结果。

（3）练习法：进行大量的九九乘法表练习题，通过实际的计算来加深对乘法结果的记忆和理解。

5. 培养对九九乘法表的兴趣和理解对于九九乘法表这样的基础知识，我们可以通过一些趣味的方法来培养兴趣和理解。

1.2.3 图乘法图乘法是关于的简化计算方法。

在一定的应用条件下，图乘法可给出该积分的数值解，而且是精确解。

（一）图乘法的适用条件（1）杆件为直杆；（2）EI为常数（等截面）；（3）和图中至少应有一个直线图形。

对于等截面直杆所构成的梁和刚架，都能同时满足以上三个条件，因而均可采用弯矩图图乘的方法，简称图乘法。

（二）图乘法计算位移的公式（1-15）式中为、图中某一图形的面积；为与该截面形心对应的另一个图形的竖标。

这样，就将较为复杂的积分运算问题简化为求图形的面积、形心和标距等几何运算问题。

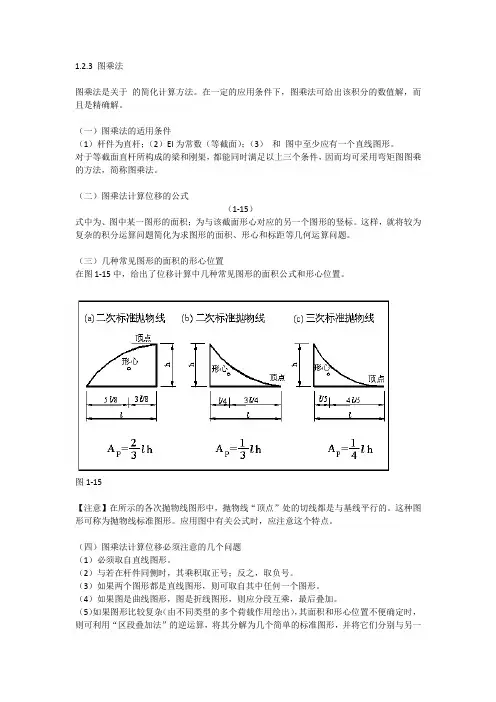
（三）几种常见图形的面积的形心位置在图1-15中，给出了位移计算中几种常见图形的面积公式和形心位置。

图1-15【注意】在所示的各次抛物线图形中，抛物线“顶点”处的切线都是与基线平行的。

这种图形可称为抛物线标准图形。

应用图中有关公式时，应注意这个特点。

（四）图乘法计算位移必须注意的几个问题（1）必须取自直线图形。

（2）与若在杆件同侧时，其乘积取正号；反之，取负号。

（3）如果两个图形都是直线图形，则可取自其中任何一个图形。

（4）如果图是曲线图形，图是折线图形，则应分段互乘，最后叠加。

（5）如果图形比较复杂（由不同类型的多个荷载作用绘出），其面积和形心位置不便确定时，则可利用“区段叠加法”的逆运算，将其分解为几个简单的标准图形，并将它们分别与另一个图形图乘，最后叠加。

（6）如果杆件EI分段变化时，可分段图乘，最后叠加。

（7）如果EI沿杆长连续变化或是曲杆和拱结构，则必须用积分计算位移。

（五）图乘法的计算步骤（1）绘实际荷载作用下的图；（2）根据所求位移，加相应单位力，绘图；（3）代入式（1-15）求位移：【注意】根据计算结果的正负号，判定位移的实际方向，并在计算值之后所加的圆括号中，标明其实际方向。

递推法求九九乘法表
（原创版）
目录
1.递推法的概念
2.递推法在九九乘法表中的应用
3.递推法求九九乘法表的具体步骤
4.递推法求九九乘法表的优点
正文
一、递推法的概念
递推法是一种数学方法，它是通过已知的数学关系，逐步推导出更高层次的数学关系。

在数学中，递推法被广泛应用于各种数学问题的求解，如数列、组合等。

二、递推法在九九乘法表中的应用
九九乘法表是数学中的一个基础概念，它包含了所有数字的两两相乘的结果。

在传统的数学教学中，我们通常通过死记硬背的方式来记住九九乘法表，但这种方式既耗时又耗力。

而递推法的应用，可以让我们通过简单的计算，就能推导出九九乘法表。

三、递推法求九九乘法表的具体步骤
1.首先，我们设定一个初始值，通常取 1。

2.然后，根据乘法的基本原理，我们可以得到一个递推公式：An = n*(n-1)。

其中，An 表示第 n 行的乘法结果，n 表示乘数。

3.接着，我们按照递推公式，逐步计算出九九乘法表中的每一个数字。

四、递推法求九九乘法表的优点
1.递推法求九九乘法表的优点在于，它不需要我们死记硬背，只需要
通过简单的计算，就能推导出九九乘法表。

2.其次，递推法求九九乘法表的过程，也是一种很好的数学思维训练，可以帮助我们理解和掌握乘法的基本原理。

1.2.3图乘法图乘法是关于的简化计算方法。

在一定的应用条件下，图乘法可给出该积分的数值解，而且是精确解。

（一）图乘法的适用条件（1）杆件为直杆；（2）E I为常数（等截面）；（3）和图中至少应有一个直线图形。

对于等截面直杆所构成的梁和刚架，都能同时满足以上三个条件，因而均可采用弯矩图图乘的方法，简称图乘法。

（二）图乘法计算位移的公式（1-15）式中为、图中某一图形的面积；为与该截面形心对应的另一个图形的竖标。

这样，就将较为复杂的积分运算问题简化为求图形的面积、形心和标距等几何运算问题。

（三）几种常见图形的面积的形心位置在图1-15中，给出了位移计算中几种常见图形的面积公式和形心位置。

图1-15【注意】在所示的各次抛物线图形中，抛物线“顶点”处的切线都是与基线平行的。

这种图形可称为抛物线标准图形。

应用图中有关公式时，应注意这个特点。

（四）图乘法计算位移必须注意的几个问题（1）必须取自直线图形。

（2）与若在杆件同侧时，其乘积取正号；反之，取负号。

（3）如果两个图形都是直线图形，则可取自其中任何一个图形。

（4）如果图是曲线图形，图是折线图形，则应分段互乘，最后叠加。

（5）如果图形比较复杂（由不同类型的多个荷载作用绘出），其面积和形心位置不便确定时，则可利用“区段叠加法”的逆运算，将其分解为几个简单的标准图形，并将它们分别与另一个图形图乘，最后叠加。

（6）如果杆件E I分段变化时，可分段图乘，最后叠加。

（7）如果E I沿杆长连续变化或是曲杆和拱结构，则必须用积分计算位移。

（五）图乘法的计算步骤（1）绘实际荷载作用下的图；（2）根据所求位移，加相应单位力，绘图；（3）代入式（1-15）求位移：【注意】根据计算结果的正负号，判定位移的实际方向，并在计算值之后所加的圆括号中，标明其实际方向。

九九乘法表的运用（数学知识点）九九乘法表是每个小学生学习数学时都要掌握的重要内容之一。

它不仅仅是一种乘法口诀，更是数学知识的基石和应用的起点。

在本文中，我们将探讨九九乘法表的运用，以及相关的数学知识点。

九九乘法表可以说是孩子们学习数学的第一步，它由1乘1到9乘9的表格组成。

每个格子都是两个数字相乘的结果。

通过九九乘法表，孩子们能够不断地重复和巩固乘法运算，从而熟练掌握基本的乘法口诀。

此外，九九乘法表还可以帮助孩子们培养记忆能力，提高专注力和逻辑思维能力。

除了学习乘法口诀外，九九乘法表还有很多有趣的应用。

首先，通过观察九九乘法表的规律，孩子们可以发现其中的一些有趣现象。

例如，每一行的数字都按照从小到大的顺序排列，每一列的数字都按照从小到大的顺序排列。

这种规律性的排列不仅让九九乘法表更加美观，也便于记忆和运算。

其次，九九乘法表可以用来解决一些实际问题。

例如，如果我们需要计算某一个两位数和九九乘法表中的某一个数字相乘的结果，可以通过查表的方式快速获得答案。

这在实际生活中会带来很多便利，特别是在没有计算器或者电子设备的情况下。

此外，九九乘法表还可以与其他数学知识点进行结合。

例如，在学习分数的概念时，我们可以利用九九乘法表来做分数的加减乘除运算。

通过将分数与九九乘法表的数字相乘或相除，孩子们可以更好地理解分数的运算规则和性质。

在实际教学中，我们可以通过多种方式来运用九九乘法表。

教师可以设计一些游戏和活动，让学生们在玩耍中学习。

例如，猜数游戏，教师可以说出两个数字相乘的结果，学生需要迅速找到对应的乘法算式。

这样既可以检验学生的记忆能力，又能增加学生的兴趣和参与度。

除了教学中的应用，九九乘法表还可以在日常生活中起到很大的作用。

例如，当我们在商场购买商品时，如果知道某个商品的单价和数量，我们可以利用九九乘法表来快速计算出总价。

这对于提高计算的速度和准确性都有很大的帮助。

综上所述，九九乘法表是数学学习的基础，也是实际生活中的应用工具。

P99是一种在计算机科学中常用的算法性能指标，它表示在给定时间内，99%的请求或操作所需的时间。

这个指标可以帮助我们了解一个算法或程序的响应时间。

以下是一个关于如何计算P99的算法的详细说明：假设我们有一个请求队列，每个请求都有一个开始时间和结束时间。

我们想要计算出队列中99%的请求所需的时间。

步骤如下：1. 初始化一个变量`max_time` 为队列中的最大时间。

2. 初始化一个变量`p99_time` 为队列中的最小时间。

3. 遍历队列中的每一个请求：* 如果当前请求的结束时间大于`max_time`，则将`max_time` 更新为当前请求的结束时间。

* 如果当前请求的开始时间小于`p99_time`，则将`p99_time` 更新为当前请求的开始时间。

4. 返回`p99_time`，这就是队列中99%请求所需的时间。

这个算法的关键在于对队列中的请求进行排序，并且确保每个请求只被处理一次。

如果一个请求已经被处理过，那么它就不会被再次处理。

这个算法的时间复杂度是O(n log n)，其中n 是队列中的请求数量。

下面是一个使用Python实现的例子：```pythondef calculate_p99(requests):# 对请求进行排序requests.sort(key=lambda x: x[1]) # x[1] 是请求的结束时间# 初始化最大和最小时间max_time = requests[0][1] # 第一个请求的结束时间是最小时间min_time = requests[-1][0] # 最后一个请求的开始时间是最大时间# 遍历剩余的请求for i in range(len(requests) - 1):if requests[i + 1][1] > max_time:max_time = requests[i + 1][1] # 如果下一个请求的结束时间大于当前的最大时间，更新最大时间if requests[i][0] < min_time:min_time = requests[i][0] # 如果下一个请求的开始时间小于当前的最小时间，更新最小时间return min_time # 返回最小时间，即P99的时间```这个函数接受一个请求列表作为输入，每个请求都是一个元组，包含一个开始时间和一个结束时间。