10-11-3级高等数学(B)期末试卷
- 格式:pdf
- 大小:159.73 KB
- 文档页数:4
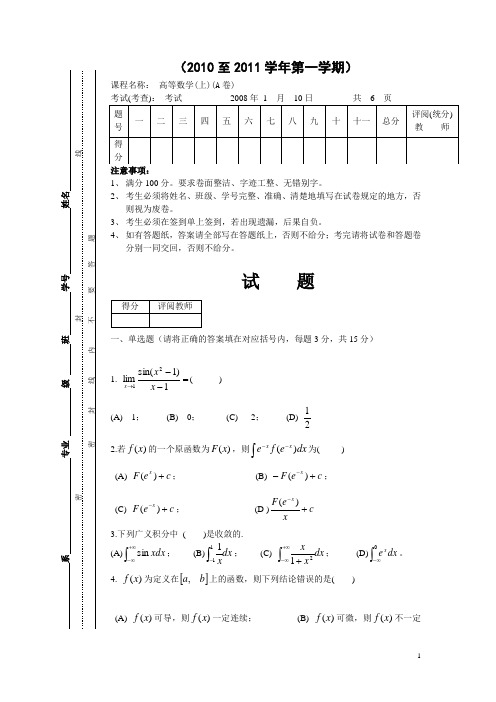
(2010至2011学年第一学期)课程名称: 高等数学(上)(A 卷)考试(考查): 考试 2008年 1 月 10日 共 6 页 注意事项:1、 满分100分。
要求卷面整洁、字迹工整、无错别字。
2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否则视为废卷。
3、 考生必须在签到单上签到,若出现遗漏,后果自负。
4、 如有答题纸,答案请全部写在答题纸上,否则不给分;考完请将试卷和答题卷分别一同交回,否则不给分。
试 题一、单选题(请将正确的答案填在对应括号内,每题3分,共15分)1. =--→1)1sin(lim21x x x ( ) (A) 1; (B) 0; (C) 2; (D)212.若)(x f 的一个原函数为)(x F ,则dx e f e xx )(⎰--为( )(A) c e F x +)(; (B) c eF x+--)(;(C) c e F x+-)(; (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ; (B)dx x⎰-111; (C) dx x x ⎰+∞∞-+21; (D)⎰∞-0dx e x。
4. )(x f 为定义在[]b a ,上的函数,则下列结论错误的是( )(A) )(x f 可导,则)(x f 一定连续; (B) )(x f 可微,则)(x f 不一定可导;(C) )(x f 可积(常义),则)(x f 一定有界; (D) 函数)(x f 连续,则⎰xadt t f )(在[]b a ,上一定可导。
5. 设函数=)(x f nn x x211lim++∞→ ,则下列结论正确的为( )(A) 不存在间断点; (B) 存在间断点1=x ; (C) 存在间断点0=x ; (D) 存在间断点1-=x二、填空题(请将正确的结果填在横线上.每题3分,共18分)1. 极限=-+→xx x 11lim 20 _____.2. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-,则该方程的通解为 .4. 设)(x f 在2=x 处连续,且22)(lim2=-→x x f x ,则_____)2(='f5.由实验知道,弹簧在拉伸过程中需要的力F (牛顿)与伸长量s 成正比,即ks F =(k 为比例系数),当把弹簧由原长拉伸6cm 时,所作的功为_________焦耳。

高数试卷(一)(上册)一、单项选择题(每题4分,共20分,把选择题答案填在括号里)1.当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则( ).A.11, 6a b ==B.11, 6a b =-= C.11, 6a b ==- D.11, 6a b =-=-2.函数2()sin πx x f x x-=的可去间断点的个数为( ).A.1B.2C.3D.无穷多个3.曲线321x y x =-的渐近线有( ).A.1条B.2条C.3条D.4条 4.下面等式正确的是( ).A. d ()()f x f x '⎡⎤'=⎣⎦⎰B.()d()d ()f x x f x =⎰C.d ()d ()d f x x f x C x =+⎰ D.d ()d ()d ba f x x f x x=⎰ 5.已知广义积分2d 1xkx+∞+⎰收敛1(0k >),则k =( ).A.π22π2 D.2π4二、填空题(每题4分,共20分)6.222111lim π2ππn n n n n n →∞⎛⎫+++= ⎪+++⎝⎭. 7.设函数)(x y y =由方程y x xy+=2所确定,则d x y== .8.设⎩⎨⎧-=-=),1e (,π)(3tf y t f x 其中f 可导且(0)0f '≠,则0d d t y x == . 9.不定积分6d (1)xx x =+⎰. 10.定积分π322π2(sin cos )d x x x -+=⎰ . 三、计算题(每题7分,共28分)11.求极限0x →.12.曲线y =的切线与x 轴和y 轴围成一个图形,记切点的横坐标为a ,试求切线方程和这个图形的面积S .当切点沿曲线趋于无穷远时,该面积的变化趋势如何?13.求不定积分⎰.14.已知21()e d xt f x t -=⎰,求10()d f x x ⎰.四、证明题(本题6分)15.设)(x f 在[0,1]上连续,在(0,1)内可导,且1233()d (0)f x x f =⎰,求证:在(0,1)内存在一点ξ使()0f ξ'=.五、讨论题(每小题8分,共16分)16.已知⎪⎩⎪⎨⎧≤+>+=.0),ln(,0,1sin )(2x x a x bx x x x f 试讨论 (1)a 、b 取何值时,)(x f 在0=x 点连续;(2)a 、b 取何值时,)(x f 在0=x 点可导,并求)0(f '.17.讨论函数0()(4)d xF x t t t =-⎰在[1,5]-上的增减性、极值和凹凸区间及拐点.六、应用题(本题10分)18.设2y x =定义在[0,1]上,t 为[0,1]上任意一点,试问t 为何值时,参考答案一、1.C ;2.B ;3.C ;4.A ;5.D .二、6.1;7. x d )12(ln -;8.3;9.61ln ln(1)6x x C -++;10.2π. 三、11.解 因为当0→x 时,x x x x 232sin 31~1sin 1-+, x x 2~1e 2-, 22~tan x x ,所以,2222001sin 13lim lim (e 1)tan 2x x x x xxx x →→=-⋅ 2221sin 1sin 1666x x x x ⎛⎫=⋅=⋅= ⎪⎝⎭. 12.解 由题设可知切点的横坐标为0>a,代入曲线方程y =可求的切点坐标为a ⎛⎝,因为312212y x x --''⎛⎫'===-= ⎪⎝⎭,所以,曲线在该点的切线斜率x ak y ='==,切线方程为)y x a =-,即230x a +-=.分别令0y =和0,x =得切线在x 轴和y 轴上的截距分别为3, X a Y ==,切线与x 轴和y 轴围成一个图形为直角三角形AOB ∆,(如图所示)其面积为a a a XY S 492332121=⋅⋅==.因为+∞==+∞→+∞→a S a a 49limlim ,049lim lim 00==++→→a S a a , 故当切点沿曲线趋于x 轴正方向无穷远时,面积S 趋于无穷大;当切点沿曲线趋于y 轴正方向无穷远时,面积S 趋于零.13.解 设sin x t =,ππ,22t ⎡⎤∈-⎢⎥⎣⎦,则 原式1cos d sin cos tI t t t==+⎰,若设2sin d sin cos tI t t t=+⎰,则121cos sin d cos sin t tI I t t C t t++==++⎰,122cos sin d ln sin cos cos sin t tI I t t t C t t--==+++⎰,故()11ln cos sint 2I t t C =+++(1arcsin ln 2x x C =+++. 14.解 由题设可得2()e x f x -'=,(1)0f =,则111201()d ()()d 0e d 0x f x x xf x xf x x x x -'=-=-⎰⎰⎰ 122101111e d()(e 1)1222e x x --⎛⎫=-=-=- ⎪⎝⎭⎰. 四、15.证明 由积分中值定理知12323()d (), ,13f x x f ⎡⎤=∈⎢⎥⎣⎦⎰ηη, 即()(0)f f η=.于是)(x f 在[0,]η上满足罗尔定理的条件,知存在(0,)(0,1)ξη∈⊂,使()0f ξ'=.五、16.解(1)因00lim ()lim ln()ln ,x x f x a x a --→→=+= 2001lim ()lim sin 0,x x f x x bx x +-→→⎛⎫=+= ⎪⎝⎭(0)ln ,f a =要使函数)(x f 在0=x 点连续必须使函数在该点左、右极限相等且等于该点的函数值即ln 0, 1a a ==.故当1, a b =为任意实数时,函数)(x f 在0=x 点连续.(2)由于连续是可导的必要条件,所以要使)(x f 在0=x 点可导,必须首先令1a =,此时函数变为⎪⎩⎪⎨⎧≤+>+=.0),ln(,0,1sin )(2x x a x bx xx x f 又因为0()(0)ln(1)0(0)lim lim0---→→-+-'==-x x f x f x f x x1lim ln(1)ln e 1,-→=+==xx x 2001sin 01(0)lim lim sin ,0x x x bx x f x b b x x +++→→+-⎛⎫'==+= ⎪-⎝⎭要使)0(f '存在必须使其在该点左、右导数存在并相等即(0)(0)(0)11f f f b -+'''===⇒=.所以当1a =且1b =时,)(x f 在0=x 点可导,此时(0)1f '=.17.解(1)0()(4)d (4)xF x t t t x x '⎡⎤'=-=-⎢⎥⎣⎦⎰, 令()0F x '=,得驻点120, 4x x ==. (2)()24F x x ''=-,令()0F x ''=,得 32x =. (3)列表:(4(1,0)-(0,2)单减且上凸;在区间上(2,4)单减且上凹;在区间(4,5)上单增且上凹. 在0x =处取得极大值0,在4x =处取得极小值332-;)316,2(-. 五、18.解 如图所示,阴影1S 部分的面积为222331012()d 033t t S t x x t x x t =-=-=⎰, 阴影2S 部分的面积为122323221121()d 333t S x t x x t x t t t =-=-=-+⎰,故)10(3134)(2321≤≤+-=+=t t t S S t S ,从而2d 42d S t t t =-,令d 0d S t =,得驻点1210, 2t t ==. 分别求出1112(0), , (1),3243S S S ⎛⎫=== ⎪⎝⎭比较可知,当12t =时,1S 与2S 之和最小.检测题(二)(上册)一、单项选择题(每题4分,共20分,把选择题答案填在括号里)1.函数y =ln u x =能构成复合关系的区间是( ).A.1,e e⎡⎤⎢⎥⎣⎦B.(0,)∞C.1,e⎡⎫+∞⎪⎢⎣⎭D.(0,e) 2.设1010()ln , (), ()e xf x xg x xh x ===则当x 充分大时有( )A.()()()g x f x h x <<B.()()()h x g x f x <<C.()()()f x g x h x <<D.()()()g x h x f x <<3.设函数(),()f x g x 具有二阶导数,且()0g x ''<.若0()g x a =是()g x 的极值,则[()]f g x 在0x 取得极大值的一个充分条件是( ).A.()0f a '<B.()0f a '>C.()0f a ''<D.()0f a ''> 4.下面等式正确的是( ). A.21arctan d C 1x x x=++⎰; B.arcsin C x =+; C.1ln d x x C x=+⎰; D.d()d ()d baf x x f x x =⎰.5.已知广义积分11d kx x ⎰收敛2(0k >),则k =( ). A.32; B.1; C.2; D.12.二、填空题(每题4分,共20分)6.若011lim e 1x x a x x →⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦,则a = . 7.设2()()lim1()x af x f a x a →-=--,则()f x 在x a =取得极 值.8.若曲线321y x ax bx =+++有拐点(1,0)-则b = . 9.定积分π32π2(sin cos )d x x x -+=⎰ . 10.不定积分22d (1)(4)x xx x =++⎰.三、计算题(每题8分,共32分)11.求极限20ln(1)lim sin x x x x x→+-. 12.已知 ⎩⎨⎧+==),1ln(,arctan 2t y t x 求22d 1d y t x =.13.设可导函数()y y x =由方程2200e d sin d x yxt t x t t --=⎰⎰确定,求d 0d yx x =.14.分别用第一换元法(凑微分法)和第二换元法求不定积分.四、讨论题(12分)15.设函数⎪⎩⎪⎨⎧>+=<+=,0,1e ,0,,0,1)(2x x x x x x f x αα试讨论α的值在什么范围内,函数满足(1)在0x =点有极限;(2)在0x =点连续;(3)在0x =点可导.五、应用题(本题10分)16.设位于曲线)y x t =≤≤下方,x 轴上方的区域为G ,求(1)G 绕x 轴旋转一周所得空间区域的体积()V t ;(2)当t 为何值时,该旋转体的体积()V t 最大?最大体积是多少?六、证明题(6分)17.设)(x f 在[0,)+∞上连续,在(0,)+∞内可导,如果存在两个正数12k k 、满足1212(0)()d 0k k k k f f x x +-=⎰,证明:存在ξ0>使()0f ξ'=.检测题(二)参考答案一、1.A ;2.C ;3.B ;4.B ;5.D .二、6.2;7.大;8.3;9.34;10.2211ln 64x C x +++.三、11.解 因为当0→x 时,22~)1ln(x x x x ⋅+,所以,222000ln(1)3lim lim lim sin sin 1cos x x x x x x x x x x x x x→→→+⋅==--- 061limsin 6x x x →==. 12.解 因为2d 2, d 1y t t t =+2d 1d 1x t t=+,所以 22d d d 212 d d d 11y y t t t t x x t t +===+, 2222d d d 2d d 2(1)d d d 11y y t x t x x t t⎛⎫⎪⎝⎭===++, 22211d 2(1)4d t t y t x ===+=. 13.解 由题设可知2200e d sin d x yxt t x t t --=⎰⎰,方程两边同时求导得2()220e(1)sin d sin xx y y t t x x --'-=+⎰,把0x =代入上述等式得1y '=,故d 10d yx x ==.14.解法1 凑微分法2C===.解法2 第二类换元积分法==设11sin22x t-=π2t⎛⎫<<⎪⎝⎭,则原式1cos d d2t t t==⎰arcsin(21)t C x C=+=-+.解法3 第二类换元积分法x=⎰,令2πsin02x t t⎛⎫=<<⎪⎝⎭,则d2sin cos dx t t t=,所以原式112sin cos d2dsin cost t t tt t=⋅⋅=⎰⎰2t C C=+=.四、解(1)因为00lim()lim(1)1,x xf x x--→→=+=00lim()lim(e1)1,xx xf x x++→→=+=α可见α是任意实数时,函数在0x=点左、右极限都相等.(2)又因为2(0)f=α,要使函数)(xf在0=x点连续必须使函数在该点极限值等于该点的函数值,即21,1a==±α.故当1±=α时,函数)(xf在0=x点连续.(3)由于连续是可导的必要条件,所以要使)(xf在0=x点可导,必须首先令21=α,此时函数变为⎪⎩⎪⎨⎧>+=<+=,0,1e ,0,1,0,1)(x x x x x x f x α0()(0)(1)1(0)lim lim 10x x f x f x f x x---→→-+-'===-, 00(e 1)1(0)lim lim e ,x x x x x f x+++→→+-'===ααα 要使)0(f '存在必须使其在该点左、右导数存在并相等,即(0)(0)(0) 1 1f f f -+'''====⇒=αα.所以当1=α时,)(x f 在0=x 点可导,此时(0)1f '=. 五、16.解 (1)222e ee 11()πd πd πd ln (1ln )1ln ttt x V t y x x x x x x ===++⎰⎰⎰ []e ππarctan(ln )πarctan(ln )4t x t ⎛⎫==- ⎪⎝⎭.(2)因为2π()0 (e)(1ln )V t t t t '=>>+,这说明()V t 在[e,)+∞上单调递增,所以当t →+∞时,()V t 取得最大值,其最大值为[]2max e πππ()πlim arctan(ln )π244tt V t x →+∞⎛⎫==-= ⎪⎝⎭. 六、17.证明 由积分中值定理知[]1212112()d (), ,k k k f x x k f k k k +=∈+⎰ηη,代入题设等式得()(0)f f η=.于是)(x f 在[0,]η上满足罗尔定理的条件,知存在112(0,)[,](0,)k k k ∈⊂+⊂+∞ξη,使()0f ξ'=.。

华南农业大学期末考试试卷(A 卷)2009学年第2学期 考试科目: 高等数学B Ⅱ 考试类型:(闭卷)考试 考试时间:120分钟学号 姓名 年级专业一、 填空题(本大题共5小题,每小题3分,共15分)1. 试定义函数在点的值的 ,使得函数在该点连续。
2.函数在点处可微分的必要条件是函数在该点处连续或可偏导;充分条件是函数的偏导数在该点处连续。
3.设函数在闭区域上连续,且,则。
4. 判断敛散性:已知且,则是收敛的。
5. 已知某二阶常系数非齐次线性微分方程的通解为,则该微分方程为。
二、选择题(本大题共5小题,每小题3分,共15分) 1. 直线与平面的交点是(B )。
(A )(9,2,-3)。
(B )(2,9,11)。
(C )(2,11,13)。
(D )(11,9,2)。
2. 若级数在处收敛,则此级数在处(A )。
(A )绝对收敛。
(B )条件收敛。
(C )发散。
(D )收敛性不能确定。
3.二元函数 在点处 (C )(A )连续,偏导数存在。
(B )连续,偏导数不存在。
(C )不连续,偏导数存在。
(D )不连续,偏导数不存在。
4. 设是连续的奇函数,是连续的偶函数, ,则以下结论正确的是( A )。
(A ) 。
(B ) 。
(C ) 。
(A ) 。
5. 微分方程的一个特解应具有形式(A,B,C 是待定常数)( B )。
(A )。
(B )。
(C )。
(D )。
三、计算题(本大题共5小题,每小题6分,共30分) (1)设,其中和具有连续导数,求。
【解】(2)求由方程所确定的函数的全微分。
【解】方程两边求微分得 整理得(3)交换积分次序。
【解】(4)求差分方程在给定初始条件下的特解。
【解】特征方程为,所以对应的齐次方程的通解为。
又不是特征根,故可令特解为,代入原方程,得比较系数可得,,故非齐次方程的一个特解为,于是非齐次方程的通解为,由所给初始条件,可得,所以方程满足给定初始条件下的特解为。

高等数学期末考试试卷大学高等数学期末考试试卷一、选择题(共30题,每题2分,共60分)在每小题给出的四个选项中,只有一个问题的解是正确的,请将正确答案填写在答题卡上。
1. 设函数f(x) = 2x^3 - 3x^2 + 6x - 9,则f'(x)的值是:A. 6x^2 - 6x + 6B. 6x^2 - 6x - 6C. 6x^2 - 6xD. 6x^2 + 6x - 62. 某实数集合S中的元素都满足条件|x - 5| < 2,则S的取值范围是:A. (3,7)B. [3,7)C. (3,7]D. [3,7]3. 已知二次曲线y = ax^2 + bx + c的顶点坐标为(1,-2),则该二次曲线的解为:A. x = -1, y = 0B. x = 1, y = 0C. x = -1, y = 4D. x = 1, y = 44. 设函数f(x) = |x - 3| + |x - 4|,则f(x)的最小值为:A. 0B. 1C. 2D. 35. 已知椭圆的中心为原点O,长轴为4,短轴为2,则该椭圆的方程为:A. x^2/4 + y^2/2 = 1B. x^2/2 + y^2/4 = 1C. x^2/16 + y^2/4 = 1D. x^2/4 + y^2/16 = 1...二、填空题(共10题,每题4分,共40分)根据题目要求,将正确的答案填写在答题卡上。
6. 设函数y = sin(x),则y'' + y = ____。
7. 设函数f(x) = 2x^2 - x - 1的极值点坐标为(x_0, y_0),则x_0的值为____。
8. 若e^a = 3,e^b = 4,则e^(a+b)的值为____。
9. 曲线y = e^x在点(0,1)处的切线方程为____。
10. 若集合A中共有n个元素,集合B中共有m个元素,且n < m,则集合B中共有____个子集。
...三、计算题(共5题,每题10分,共50分)根据题目要求,进行计算,并将结果填写在答题卡上。


高等数学b1期末试题及答案一、选择题(每题5分,共30分)1. 下列函数中,哪一个是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x答案:B2. 计算定积分∫(0,1) x^2 dx 的值。
A. 1/3B. 1/2C. 1D. 2答案:A3. 以下哪个选项是洛必达法则的应用?A. 计算极限lim(x→0) (sin x)/xB. 计算定积分∫(0,π) sin x dxC. 计算导数 d/dx (x^3)D. 计算不定积分∫e^x dx答案:A4. 以下哪个选项是二阶导数?A. d^2y/dx^2B. dy/dxC. d^2y/dy^2D. d^2y/dxdy答案:A5. 以下哪个选项是泰勒公式的展开式?A. f(x) = f(a) + f'(a)(x-a)B. f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2!C. f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2D. f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^3/3!答案:B6. 以下哪个选项是傅里叶级数的组成部分?A. 正弦函数B. 余弦函数C. 指数函数D. 所有选项答案:D二、填空题(每题5分,共20分)1. 函数 f(x) = x^3 - 6x 在 x = 2 处的导数是 _______。
答案:-62. 微分方程 y'' - 2y' + y = 0 的通解是 _______。
答案:y = C1 * e^x + C2 * e^(-x)3. 计算极限lim(x→0) (e^x - 1)/x 的值是 _______。
答案:14. 函数 y = sin x 的不定积分是 _______。


高等数学试卷一、 单项选择题(本题共5小题,每小题4分,满分20分)1. 由[,]a b 上连续曲线y = g (x ),直线x a =,x b =()a b <和x 轴围成图形的面积S =( ).(A)dx x g ba⎰)((B)dx x g ba⎰)((C) dx x g ba⎰)((D)2))](()([a b a g b g -+2.下列级数中,绝对收敛的是( )(A )()∑∞=--11321n nn n (B )()∑∞=-+-11)1ln(311n n n(C )()∑∞=-+-12191n n n n (D )3.设),(),,(y x v v v x f z ==其中v f ,具有二阶连续偏导数.则=∂∂22y z( ).(A)222y v v f y v y v f ∂∂⋅∂∂+∂∂⋅∂∂∂ (B)22y v v f ∂∂⋅∂∂(C)22222)(y v v f y v v f ∂∂⋅∂∂+∂∂∂∂ (D)2222yv v f y v v f ∂∂⋅∂∂+∂∂⋅∂∂4.⎰-1121dx x ( )(A )2 (B )-2(C )0 (D )发散5. 求微分方程2x y =''的通解( )(A )21412c x c x y ++= (B)cx x y +=124 (C )c x y +=124 (D )221412c x c x y ++= 二、 填空(本题共5小题,每小题4分,满分20分)1. 若⎰=22sin 3)(x dt t x x f ,则()f x '=2. 设f (x ,y )是连续函数,交换积分次序:⎰⎰⎰⎰+212141410),(),(yy ydx y x f dy dx y x f dy =3.幂级数()()∑∞=--121!21n nn n x 的收敛半径是4. 已知5)2(,3)2(,1)0('===f f f ,则⎰=2'')(dx x xf通解为x ce y x+=的微分方程为三、 计算下列各题(本题共4小题,每小题5分,满分20分)1. x y z cos )(ln =,求。


武汉大学2020-2021第一学期高等数学B1期末试卷 A 卷1、(9分) 求极限: 011lim e 1x x x →⎛⎫− ⎪−⎝⎭. 2、(9分)已知曲线满足方程2e 0xy x y ++=,求曲线在点(0,1)−处的法线方程. 3、(10分)求由曲线e ,ln ,1,2x y y x x x ====所围成的图形的面积. 4、(10分)(1)求齐次线性微分方程20y y y ''''''−−=的通解;(2)求该方程满足初始条件(0)0,(0)(0)3y y y '''===的特解.(3)对于非齐次方程221e x y y y x ''''''−−=+,用待定系数法给出特解的形式(无需求出其中的待定系数的数值).5、(9分)求极限lim nn n →∞⎛ ⎪⎝⎭.6、(7分)求不定积分x ⎰.7、(7分)设2()ln(1)f x x =+,计算反常积分20()d ()+2()5f x x f x f x +∞'+⎰.8、(7分) 求极限:2cos 1e d lim (sin )xt x tx x x −→+⎰.9、(7分)等角螺线的极坐标方程为e θρ=,在0θ=附近,其在直角坐标系下可由函数()y y x =表示,试求0d d y x θ=以及220d d yx θ=.10、(7分)计算星形线33cos ,sin x a t y a t⎧=⎪⎨=⎪⎩的弧长,其中0,[0,2]a t π>∈. 11、(7分)计算函数231sin ,0()0,0x x x f x xx ⎧+≠⎪=⎨⎪=⎩的导函数;并讨论:是否存在0δ>,使得函数()f x 在区间(,)δδ−内单调递增?说明理由. 12、(6分)求解常微分方程:532e 0x xy y x y '++=.13、(5分)设函数()f x 在区间[],a b 上有连续的二阶导数,证明:至少存在一点(,)a b ξ∈使得3()()d ()()224baa b b a f x x b a f f ξ+−⎛⎫''=−+⎪⎝⎭⎰.武汉大学2019-2020第一学期高等数学B1期末试卷 A 卷 参考解答1、(9分) 求极限011lim e 1xx x →⎛⎫− ⎪−⎝⎭. 解: 200011e 1e 1lim lim lim e 1(e 1)x x x xx x x x x x x x →→→⎛⎫⎛⎫−−−−⎛⎫−== ⎪ ⎪ ⎪−−⎝⎭⎝⎭⎝⎭ 5分0e 11lim 22x x x →⎛⎫−== ⎪⎝⎭ 9分2、(9分)已知曲线满足方程2e 0xy x y ++=,求曲线在点(0,1)−处的法线方程. 解:对方程2e 0xy x y ++=两边关于x 求导得:212e ()0xy y y xy ''+++=,4分 代入0,1x y ==−解得0,11x y y ==−'=.7分 因此,法线的斜率为1−,在点(0,1)−处的法线方程为:1y x =−−.9分3、(10分)求由曲线e ,ln ,1,2x y y x x x ====所围成的图形的面积. 解:显然当[1,2]x ∈时有e ln x x >,因此面积()21e ln d x S x x =−⎰5分22221111e d ln d e ln d x x x x x x x =−=−⎰⎰⎰8分 222211e e ln d ln e e 2ln 21x x x x =−−+=−−+⎰10分4、(10分)(1)求齐次线性微分方程20y y y ''''''−−=的通解;(2)求该方程满足初始条件(0)0,(0)(0)3y y y '''===的特解.(3)对于非齐次方程221e x y y y x ''''''−−=+,用待定系数法给出特解的形式(无需求出其中的待定系数的数值).解:(1) 该微分方程的特征方程为:3220λλλ−−=, 4分它有特征根:00,λ=21,λ=−32,λ=故而该齐次线性微分方程的通解为:2123e e x x y C C C −=++6分 (2)代入初值条件得方程组:12323230,23,43C C C C C C C ++=−+=+=,解得:1230,1,1C C C ==−=,得微分方程的特解为:2e e x x y −=−. 8分 (3)特解的形式为:2123()e x y C x x C C x *=++.10分5、(9分)求极限lim nn →∞⎝⎭.解: lim ln lim 1lim een n nn n n n →∞→∞⎫⎪⎪⎝⎭⎝⎭→∞== ⎪⎝⎭5分12eee n n n===9分6、(7分)求不定积分x ⎰.解:()21d arcsin arcsin x x x =⎰4分 1arcsin C x=−+7分7、(7分)设2()ln(1)f x x =+,计算反常积分2()d ()+2()5f x x f x f x +∞'+⎰. 解: 2200()1d d ()()+2()5(()+1)4f x x f x f x f x f x +∞+∞'=++⎰⎰ 3分 2001()11ln(1)1arctan arctan 2222f x x +∞+∞+++==5分 11arctan 222π⎛⎫=− ⎪⎝⎭7分8、(7分) 求极限:2cos 1e d lim (sin )xt x tx x x −→+⎰.解:22cos cos 112e d e d lim lim(sin )2xxt t x x ttx x x x−−→→=+⎰⎰3分2cos 0e sin lim 4x x xx−→−= 5分11e 4−=− 7分9、(7分)等角螺线的极坐标方程为e θρ=,在0θ=附近,其在直角坐标系下可由函数()y y x =表示,试求0d d y x θ=以及220d d yx θ=.解:可以将方程改写成参数方程e cos e sin x y θθθθ⎧=⎪⎨=⎪⎩,则d d d 0d 0e cos e sin cos sin e co 1s e sin cos d n d si y xyx θθθθθθθθθθθθθθθθθθ=======+−−=+4分()()222(cos sin )(cos sin )cos sin (cos sin )2s d d d 2d d d d d d d co s n 0i d c =2e os e sin d y x x x yx θθθθθθθθθθθθθθθθθθθθθθ====−+++−−=−== 7分10、(7分)计算星形线33cos ,sin x a t y a t⎧=⎪⎨=⎪⎩的弧长,其中0,[0,2]a t π>∈. 解:曲线弧长220s t t ππ==⎰⎰4分220312cos sin d 6a t a t t t a ππ===⎰⎰7分11、(7分)计算函数231sin ,0()0,0x x x f x xx ⎧+≠⎪=⎨⎪=⎩的导函数;并讨论:是否存在0δ>,使得函数()f x 在区间(,)δδ−内单调递增?说明理由.解:当0x ≠时,323131()12sincos f x x x x x'=+−,另一方面, 2301sin(0)lim1x x x x f x→+'==,因此32313112sin cos ,0()1,0x x f x x x x x ⎧+−≠⎪'=⎨⎪=⎩ 3分对任意0δ>,取0x =,显然00x δ<<且01x <,代入()f x '可得: 003()10f x x '=−<,由于导函数()f x '在0x 处连续,存在0ε>使得00[,](,)x x εεδδ−+⊂−,且()f x '在区间00[,]x x εε−+内小于0,即有()f x 在区间00[,]x x εε−+单调递减,因此,不存在0δ>,使得函数()f x 在区间(,)δδ−内单调递增.7分12、(6分)求解常微分方程:532e 0x xy y x y '++=.解:显然0y ≡是方程的特解;当0y ≠时方程两边同除以3xy 的方程:3242e 0x y y y x x−−'++=, 令2z y −=,有3d d 2d d z y y x x−=−,原方程就可化为如下线性方程: 3分2442e x z y x x−'=+,用一阶线性微分方程的求解公式得:24(2e )x y z x C −==+ 6分13、(5分)设函数()f x 在区间[],a b 上有连续的二阶导数,证明:至少存在一点(,)a b ξ∈使得3()()d ()()224baa b b a f x x b a f f ξ+−⎛⎫''=−+⎪⎝⎭⎰. 证明:令()()d x aF x f t t =⎰,由于()f x 在区间[],a b 上有连续的二阶导数,因此()F x 在区间[],a b 上有连续的三阶导数,取02a bx +=,由泰勒公式得: 23010000010()()()()()()()(),(,)2!3!F x F F a F x F x a x a x a x a x ξξ''''''=+−+−+−∈ 23020000020()()()()()()()(),(,)2!3!F x F F b F x F x b x b x b x x b ξξ''''''=+−+−+−∈3分利用00()b x a x −=−−,上述两式相减得:31201020()()()()()(),(,),(,)3!2F F b a F b F a F x b a a x x b ξξξξ''''''+−⎛⎫'−=−+∈∈ ⎪⎝⎭即有:312()()()()d ()2242baf f a b b a f x x b a f ξξ''''++−⎛⎫⎛⎫=−+ ⎪ ⎪⎝⎭⎝⎭⎰. 由于()f x ''在区间[],a b 上连续,由介值定理可知至少存在一点(,)a b ξ∈使得12()()()2f f f ξξξ''''+''=. 因此3()()d ()()224baa b b a f x x b a f f ξ+−⎛⎫''=−+⎪⎝⎭⎰. 5分。

高等数学期末试卷一 选择题1.极限1(1)lim 1x x x →--的值是( )A.-1B.1C.0D.不存在2.设函数f(x)在点x=a 处可导,则(()())0lim f a x f a x x x +--→=( ) A.2f’(a) B.f’(a) C.f’(2a) D.03.使函数f(X)= )A. ]3/5,4/5⎡-⎣B. ]1,1⎡-⎣C. ]2,2⎡-⎣D. ]0,1⎡⎣4.若函数f(x)的导数是sin(x),则f(x)的一个原函数是( )A.1+sin(x)B.1-sin(x)C.1+cos(x)D.1-cos(x)5.设f(x)=1^2,0,0x xx x +⎧⎫⎨⎬≥⎩⎭则定积分11()f x dx -⎰的值是( ) A.1/2 B.7/6 C.4/3 D.11/66.抛物线y^2=2px(p>0),自(0,0)到(p/2,p )的一段弧长s=( )A. 2B.(p/2)ln (C.(P/D.(p/7.已知f(x)连续,F(X)= ^20(^2)X f t dt ⎰,则F’(X)=( )A.f(x^4)B.X^2f(x^4)C.2x f(x^4)D.2x f(x^2)8.下列结论正确的是( ) A. a ≠0, B. b •a =a •c ,则b =_c B. a ≠0, B. b ⨯a =a ⨯c ,则b =c C. b ⨯a =0,则(b •a )^2=a ^2b ^2 D. b •a =0,则b ⨯a =0二.填空题 1.设2lim()^8x x a x x a→∞+=-,则a=( ) 2.设y=f(3232x x -+),f’(x)=arctanx^2,则dy dx |x=0 =( ) 3.曲线y=xsin(lnx)(x>0)在区间( )内是凹的,在区间( )内是凸的,拐点的横坐标是( )4.已知a ={-2,2,1}, b ={m,3,n},且b ⨯a =0,则m=_____,n=______三.解题1.设y=ln(1+e^(-x^2)),求dy.2.设函数y=y(x)由方程y-xe^y=1所确定,求^2^2d ydx|x=03.求极限:ln(11/) limcot xxarc x →∞+四.试问a为何值时,函数f(x)=asinx+13sin3x在x=3π处取得极值?它是最大值还是最小值,并求出该极值。

高数三期末考试题及答案一、选择题(每题5分,共20分)1. 已知函数f(x)=x^3-3x,求f'(x)的值。
A. 3x^2-3B. 3x^2+3C. x^3-3D. x^3+3答案:A2. 计算定积分∫(0,1) x^2 dx。
A. 1/3B. 1/2C. 2/3D. 1答案:B3. 判断下列级数是否收敛。
∑(1, 2, 3, 4, ...)A. 收敛B. 发散答案:B4. 求解微分方程dy/dx+y=x的通解。
A. y = e^(-x)∫x dx + CB. y = e^(x)∫x dx + CC. y = e^(-x)∫e^x dx + CD. y = e^(x)∫e^(-x) dx + C答案:A二、填空题(每题5分,共20分)1. 函数f(x)=sinx的二阶导数是______。
答案:-cosx2. 求极限lim(x→0) (sinx/x)。
答案:13. 已知函数f(x)=x^2-4x+4,求其顶点坐标。
答案:(2, 0)4. 计算二重积分∬D xy dA,其中D为x^2+y^2≤1的闭区域。
答案:π/2三、解答题(每题10分,共30分)1. 求函数y=x^3-6x^2+9x+1的极值点。
解:首先求导数y'=3x^2-12x+9,令y'=0,解得x=1或x=3。
然后检查二阶导数y''=6x-12,发现x=1时y''<0,x=3时y''>0,因此x=1为极大值点,x=3为极小值点。
2. 计算定积分∫(0,2) (x^2-4x+4) dx。
解:首先进行积分运算,得到∫(x^2-4x+4) dx = (1/3)x^3-2x^2+4x。
然后将积分上限2和下限0代入,计算得到(1/3)(2)^3-2(2)^2+4(2)- [(1/3)(0)^3-2(0)^2+4(0)] = 8/3 - 8 + 8 = 8/3。
3. 求解微分方程dy/dx-2y=e^(2x)。


共 8 页 第 1 页《高等数学B 》课程期末试卷一.填空题(本题共9小题,每小题4分,满分3 6分)1. 幂级数1(3)3nnn x n ∞=-⋅∑的收敛域为 ; 2. 设222()z y f x y =+-,其中()f u 可微, 则yzx x z y∂∂+∂∂= ; 3. 曲线224x y z z x y++=⎧⎨=+⎩在点(1,1,2)处的法平面方程是 ;4. 设C 为曲线22241x y z z z ⎧++=⎨=⎩,则曲线积分ds z y x c222++⎰= ;5. 交换二次积分的次序⎰⎰--xx x dy y x f 2222),(dx = ;6.三次积分12220d )d x y x y z z ++⎰⎰⎰的值是 ;7. 散度()3(2,0,)div cos(2)x y y z π+-+=i j k ;8. 已知第二型曲线积分4124(4)d (65)d Bn n Ax xy x x y y y -++-⎰与路径无关,则n = ;9.平面5431x y z ++=被椭圆柱面22491x y +=所截的有限部分的面积为 . 二. 计算下列各题(本题共4小题,每小题7分,满分28分)10.设(,)z z x y =是由方程1xy yz xz ++=所确定的隐函数,0x y +≠,试求2zx y∂∂∂.共 8 页 第 2 页11.计算二重积分2()d d Dx y x y +⎰⎰,其中区域{}22(,)24D x y y x y y =≤+≤.12.设立体Ω由曲面2221x y z +-=及平面0,z z ==围成,密度1ρ=,求它对z 轴的转动惯量.13. 计算曲面积分d S z ∑⎰⎰,∑为球面2222x y z R ++=上满足0h z R <≤≤的部分.共 8 页 第 3 页三(14).(本题满分8分)求函数22(,)f x y x x y =-- 在区域{}22(,)21D x y x y =+≤上的最大值和最小值.四(15)。