静力学-计算题

静力学习题一． 填空题（40分，每题4分。

请将简要答案填入划线内）1．图示系统只受F 作用而平衡。

欲使A支座约束力的作用线与AB 成︒30角，则斜面的倾角θ 应为 。

2．物A 重100kN ，物B 重25kN ，A 物与地面的静摩擦因数为0.2，滑轮处摩擦不计。

则物体A 与地面间的摩擦力为 。

3．正六面体三边长分别为4,4,23（单位m ）；沿AB 联线方向作用了一个力F （单位kN ），其大小为F ，则该力对x 轴的力矩为 ；对z 轴的力矩为 。

4．在图示桁架中，已知F 、a ，则：杆1内力之大小为 ；杆2内力之大小为 ；杆3内力之大小为 。

5．图示结构受矩为M =10m kN ⋅的力偶作用。

若a =1m ，各杆自重不计。

则固定铰支座D 的约束力的大小为 。

一．填空题（40分，每题4分。

请将简要答案填入划线内）1．杆AB 以铰链A 及弯杆BC 支持，杆AB上作用一力偶，其力偶矩大小为M ，不计各杆自重，则A 支座反力的大小为 。

2．若F =50kN ，P =10kN ，墙与物体间的静摩擦因数f s =0.3，则摩擦力为 。

3．已知一正方体，各边长为a ，沿对角线BH 作用一力F ，则该力在x 1轴上的投影为 ，对z 轴的矩为 。

4．图示简支桁架，已知力F 1、F 2和长度a 。

则杆1内力的大小为 ；杆2内力的大小为 ；杆3内力的大小为 。

二．填空题（40分，每题4分。

请将简要答案填入划线内）1.平面系统受力偶矩为m kN 10⋅=M 的力偶作用，不计各杆自重，则A 支座反力的大小为为 kN 。

2．物A ，B 分别重P1=1kN ，P 2=0.5kN ，A 与B以及A 与地面间的摩擦因数均为f s =0.2，A ，B通过滑轮C 用一绳连接，滑轮处摩擦不计。

今在A 物块上作用一水平力F ，则能拉动物体A时该力应大于 。

3．图示悬臂桁架中，内力为零的杆有 。

4．一重为P ，边长为a 的均质正方形薄板与另一重为2P 的均质三角形薄板焊接成一梯形板，在A 点悬挂。

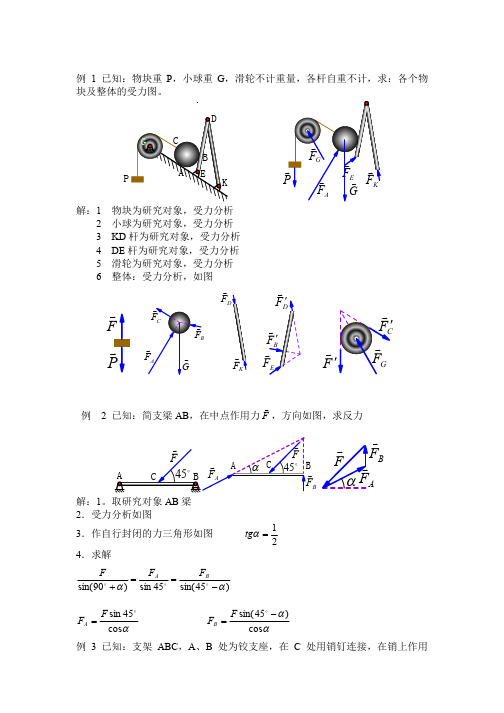
静力学计算题答案(总28页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--静力学和运动学计算题1 如图所示结构中各杆的重力均不计，D ，C 处为光滑接触，已知：P = 50 kN ，试求铰链B ，E 对杆DE 的约束力。

解：取整体为研究对象： 0=∑x F ，F Hx = 00=∑y F ，F D - P - F Hy = 0 ∑=0)(F M D，P · 70 - F Hy · 250 = 0， F Hy = 14 kN ，F D = 64 kN取ECH 为研究对象：∑=0)(F M E，F C · 100 - F Hy · 200 = 0，F C = 28 kN取ABC 为研究对象：∑=0)(F M A，F By · 90 - F C · 220 = 0，F By = kN0=∑y F ，F sin+ F By -F C -P = 0，F = 16 kN 0=∑x F ， F cos α + F Bx = 0，F Bx = kN取DE 为研究对象：0=∑x F ，2Ex F - F'Bx = 0， 2Ex F = F'Bx = F Bx = - kN0=∑y F ，F D - F'By + 2Ey F = 0，2Ey F = kN2 如图所示结构由直杆AB ，CD 及折杆BHE 组成。

已知：P = 48 kN ，L 1 = 2 m ， L 2 =3 m ，r = m ，各杆及滑轮绳索重量均不计。

求A ，D ，E 处的约束力。

解：取整体为研究对象：∑=0)(F M A，3F E - P + = 0，F E = 32 kN 0=∑x F ，F Ax = 0，0=∑y F ，F Ay = P - F E = 16 kN ，取COD 为研究对象：∑=0)(F M C，F Dy L 2 + Pr - P (21L 2 + r ) = 0，F Dy = 24 kN取BHE 为研究对象：∑=0)(F M B，- F'Dx L 1 - F'Dy L 2 + F E L 2 = 0，D y D y F F =' F'Dx = 12 kN3 不计重力的三直杆用铰连接如图所示，重物M的重力为P ，由系在销钉D并绕过GC杆C端不计直径的小滑轮，再绕过定滑轮O 的绳系住。

重修班静力学复习题一、 是非判断题（10分）1．若两个力的力矢量相等，12F F =r r ，则两个力等效。

（×） （若两个力偶的力偶矩矢相等，12M M =r r，则两个力偶等效）（√）2.根据力的可传性原理，可以将构架ABC 上的作用在AB 杆的力F 移至AC 杆图示位置。

2. 图中圆盘处于平衡状态，说明力偶M 与力F 等效。

（×）3. 空间中三个力构成一平衡力系，此三力必共面。

（√）4. 空间任意力系向某一点O 简化，主矢为零，则主矩与简化中心无关。

（√）5. 空间任意力系总可以用二个力来平衡。

（√）6. 力与轴共面则力对轴的矩为零。

（√）7. 空间平行力系不可能简化为力螺旋。

（√） 二 选择题（15分）1不经计算，可直接判断出图示桁架结构的零杆数目为 C 个。

A 2； B 3；C 4；D 5期未试题A ：（6分）图示简支桁架，已知力P 、Q ，长度a ，刚杆1，2，3的内力分别为=1T （ 0 ），=2T （ －P ），=3T （ 0 ）。

期未试题B （6分） 图示悬臂桁架受到大小均为F 的三个力作用，则杆1内力大小为（ 0），杆2内力大小为（ －F ），杆3内力大小为（ 0 ）。

2 物块重力大小为5kN G =，与水平面间的摩擦角为020f ϕ=，今用与铅垂线成025角的力F 推动物块，若5kN F G ==，则物块 A 。

A 保持静止；B 处于临界状态；C 向右加速滑动；D 向右匀速滑动期未试题：2 物块重力大小为5kN G =，与水平面间的摩擦角为030f ϕ=，今用与铅垂线成050角的力F 推动物块，若5kN F G ==，则物块（ A ）。

补考试题：物块重力大小为5kN G =，与水平面间的摩擦角为030f ϕ=，今用与铅垂线成065角的力F 推动物块，若5kN FG ==，则物块（ C ）。

3在正方体的一个侧面，沿AB 方向作用一集中力F ， 则该力对坐标轴的力矩大小为 D 。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题和2，沿同一直线但方向相反。

1．若作用在A点的两个大小不等的力则其合力可以表示为。

①1－2；②2－1；③1＋2；2．作用在一个刚体上的两个力A、B，满足A=－B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

、2、3、4为作用于刚体上的平面共点力系，其力矢4．已知关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

3．作用在刚体上的两个力等效的条件是。

静力学试题及答案一、选择题1. 在一个平衡的物体上，作用的重力和支持该物体的力的相对位置关系是：A. 重力和支持力的作用线重合B. 重力和支持力的作用线不重合答案：A2. 下列哪个不是满足平衡条件的必要条件：A. 物体受到合力为零的作用B. 物体受到合力矩为零的作用C. 物体所受合力与其自重相等反向答案：B3. 下列哪个条件不是平衡杆的平衡条件：A. 杆上所有质点的合外力为零B. 杆上所有质点的合力矩为零C. 杆上所有质点的合重力为零答案：C4. 若在一根水平杆上放置两个等质量物体，物体A在杆的左端，物体B在杆的右端，下列哪个位置组合是平衡位置：A. A在杆的中点，B在杆的左端B. A在杆的中点，B在杆的右端C. A、B均在杆的两端答案：B5. 下列哪个条件不是平衡力夹具的平衡条件：A. 物体受到合力为零的作用B. 力夹具上所有质点的合力为零C. 力夹具上所有质点的合力矩为零答案：A二、填空题1. 物体所受重力与支持力方向相反，其合力为______。

答案：零2. 物体所受重力矩与支持力矩之间的关系为______。

答案：相等且反向3. 在平衡位置，物体所受合力矩等于______。

答案：零4. 平衡力夹具上所有质点所受力矩之和等于______。

答案：零三、计算题1. 质量为10 kg的物体悬挂在离支点2 m处的杆上，求支持力的大小。

答案：由于平衡条件下物体所受合力为零，支持力的大小等于物体的重力大小，即支持力=mg=10 kg × 9.8 m/s²= 98 N。

2. 在一个长度为6 m的水平杆上有两个距离杆左端为1 m和5 m处的质量分别为4 kg和6 kg的物体，求物体B对杆的支持力和物体A对杆的支持力。

答案：物体B对杆的支持力为FB=6 kg × 9.8 m/s²= 58.8 N；物体A 对杆的支持力为FA=4 kg × 9.8 m/s²= 39.2 N。

静力学习题1,重N G 100=的物块置于水平面上，N P 50=，030=α，块与水平面的静滑动摩擦系数8.0=f ，动滑动摩擦系数78.0'=f ，求物块所受的滑动摩擦力（大小，方向）2，图示下列机构在已知载荷作用下处于平衡，试画出A 、B 两支座反力作用线的方位（不能用分量来表示）。

（有图）3，三无重杆AC 、BD 、CD 如图铰接，B 处接触光滑，ABCD 为正方形。

CD 杆受力如图所示，ql P =，在BD 上作用一力偶2ql M =。

试求(1)A 端和B 端的约束反力。

(2)E 处的反力（有图）4，如图所示，ABCD 呈正方形，外载荷为P ，求杆AC 的内力。

（下图）5，试分别画出如图所示物体系中每个物体的受力图。

（下左图）6，图所示m a 2=，受有载荷kN P 6=，m kN q /6=，m kN m ⋅=8，试求各铰链处的约束反力。

（上右图）7，均质杆在A 、B 两点分别与矩形光滑接触，并在图示情况下平衡。

AD 杆长为_______ 。

（图1）8，如图所示，物体A 重为N P 100=放在与水平面成030=α的粗糙斜面上，物体A 与斜面间的静滑动摩擦系数为1=f ，则摩擦力的大小为__ 。

（图2）图1） （图2）9，正方形ABCD ，边长m a 2=，受如图所示平面力系作用。

已知：m kN q /1=，kN F F F F 24321====。

试求力系的合成结果，并画在图上。

10，分别画出如图所示物体系中每个物体的受力图。

11，构如图示，已知m L 4=，m kN q /6=,m kN M ⋅=8，试求(1)A 、B 处约束反力。

(2)CD 杆的内力。

静力学模拟试题及答案一、选择题1. 静力学中，力的平衡状态是指：A. 物体静止不动B. 物体速度为零C. 物体加速度为零D. 物体受力为零答案：C2. 以下哪项不是静力学中的基本概念？A. 力B. 力矩C. 动量D. 平衡答案：C二、填空题1. 根据牛顿第一定律，物体在不受外力作用时，将保持________状态。

答案：静止或匀速直线运动2. 在静力学中，当物体受到多个力作用时，若这些力的合力为零，则物体处于________状态。

答案：平衡三、简答题1. 解释什么是静力学中的二力平衡，并给出一个生活中的例子。

答案：二力平衡是指两个大小相等、方向相反、作用在同一直线上的力作用在物体上，使得物体保持静止或匀速直线运动的状态。

例如，当一个人站在水平地面上时，其受到的重力和地面的支持力就是一对二力平衡的例子。

2. 描述力矩的三要素，并说明它们是如何影响力矩的大小和方向的。

答案：力矩的三要素包括力的大小、力臂的长度以及力的作用点。

力的大小越大，力臂越长，力矩就越大；力臂长度固定时，力的作用点越远离旋转轴，力矩也越大。

力矩的方向遵循右手定则，即当力的方向从旋转轴指向力的作用点时，拇指指向的方向即为力矩的方向。

四、计算题1. 一个质量为10kg的物体，受到一个水平向右的力F=20N，求物体的加速度。

答案：根据牛顿第二定律，F=ma，所以a=F/m=20N/10kg=2m/s²。

2. 一个杠杆长2m，一端固定，另一端受到一个垂直向下的力G=100N，求杠杆的力臂长度。

答案：由于杠杆平衡，力臂长度等于杠杆长度的一半，即1m。

五、论述题1. 论述静力学在工程学中的应用，并给出至少两个具体的例子。

答案：静力学在工程学中有着广泛的应用，例如：- 在建筑设计中，通过静力学分析可以确定建筑物结构的稳定性和承载能力，确保建筑物的安全。

- 在机械设计中，通过计算零件的受力情况，可以设计出既满足功能需求又具有足够强度的机械结构。

静力学练习题及参考答案1. 问题描述：一根长度为L的均质杆以一端固定在墙上，另一端悬挂一重物。

重物造成的杆的弯曲应力最大为σ。

杆的质量可以忽略不计。

计算重物的质量m。

解答：根据静力学原理，杆的弯曲应力可以用公式计算：σ = M / S，其中M是杆的弯矩，S是杆的截面横截面积。

因为杆是均质杆，所以它的截面横截面积在整个杆上都是相等的。

设杆的截面横截面积为A。

杆的弯矩M可以通过杆的长度L和重物的力矩T计算得到：M = T * (L/2)。

代入上面的公式，我们可以得到：σ = (T * (L/2)) / A。

根据题目的描述，我们可以得到如下等式：σ = (m * g * (L/2)) / A，其中g是重力加速度。

我们可以将这个等式转换成求解未知质量m的方程。

将等式两边的A乘以m，并将等式两边的m乘以g，我们可以得到如下方程：m^2 = (2 * σ * A) / (g * L)解这个方程，我们可以求得未知质量m。

2. 问题描述：一根均质杆的长度为L，质量为M。

杆的一端固定在墙上，另一端悬挂一重物。

杆与地面的夹角为θ。

重物造成的杆的弯曲应力最大为σ。

求重物的质量m。

解答：在这个问题中，除了重物的力矩，还需要考虑到重力对杆的力矩。

由于杆是均质杆，其质量可以均匀分布在整个杆上。

假设杆上的每个微小质量元都受到与其距离一致的力矩。

重物造成的力矩可以用公式计算：M1 = m * g * (L/2) * sinθ，其中g 是重力加速度。

由于杆是均质杆，它的质心位于杆的中点。

因此重力对杆的力矩可以用公式计算：M2 = M * g * (L/2) * cosθ。

根据静力学的原理，杆的弯曲应力可以用公式计算：σ = M / S，其中M是杆的弯矩，S是杆的截面横截面积。

在这个问题中，我们可以将弯曲应力的计算公式推广到杆的中点（也就是质心）：σ = (M1 + M2) / S代入上面的公式，我们可以得到：σ = ((m * g * (L/2) * sinθ) + (M *g * (L/2) * cosθ)) / S根据题目的描述，我们可以得到如下等式：σ = ((m * g * (L/2) * sinθ) + (M * g * (L/2) * cosθ)) / (A / 2)，其中A是杆的横截面积。

计算题1、系统如图，已知：不计杆、轮自重，忽略滑轮大小，起吊重量P=20kN 求：系统平衡时，杆AB,BC受力解：（1）AB、BC杆为二力杆，取滑轮B（或点B），画受力图（2）列平衡方程（3）求解（4）答2、已知：F=3kN, l=1500mm, h=200mm，忽略自重。

求：平衡时，压块C对工件与地面的压力及AB杆所受的力解：AB、BC杆为二力杆.取销钉B.3、曲柄连杆活塞机构在如图所示位置上，活塞上受到力F=400N ，试问在曲柄上应加多大的力偶矩M 才能使机构平衡。

4、已知：取起重机支架尺寸如图，自重110,P=kN 起吊重量240,P =kN 求：轴承A 、B 处的约束力5、图示简支梁ABC ，自重不计。

已知m kN q /3=，m l 2=，m kN M ⋅=60。

试求支座A 、B 的约束力。

（本题15分）6、如图所示水平梁AB，受到一均布载荷和一力偶的作用。

已知均布载荷的集度q，力偶矩的大小m=kN/m2.0=l。

不计梁本身的质量，求支座A、M，长度m5=kN1⋅B的约束反力。

7、多跨静定梁由AB 梁和BC 梁用中间铰B 连接而成，支承和荷载情况如图所示，已知F = 10kN，q = 2.5kN/m，α = 45︒；求支座A、C的反力和中间铰B 处的内力。

解：AB 梁是基本部分，BC 梁是附属部分1）先取BC梁为研究对象，列平衡方程8、多跨静定梁的尺寸及载荷如图所示，求支座及中间铰处的约束力9、多跨静定梁的尺寸及载荷如图所示，求支座及中间铰处的约束力10、图示塔式起重机，机架重为 P ，其作用线离右轨 B 的距离为 e=1.5m ，轨距为 b=3m ，最大载重 P 1 ，离右轨的最大距离为 c=10m ，平衡锤重力 P 2 的作用线离左轨 A 的距离为 a 。

欲使起重机满载和空载时均不翻倒，求平衡锤重力 P 2 的大小。

11、已知:10kN,E P =7kN,G P = 各杆长度均为1 m求: 1,2,3杆受力.用截面法,取桁架左边部分12、已知: P =10kN,尺寸如图 求桁架各杆件受力解: 取整体，画受力图13、已知：物块重P ，鼓轮重心位于1O 处，闸杆重量不计，摩擦系数s f ，各尺寸如图所示。

五、计算题1、如图所示，在由四根杆铰接而成的结构中，HK 杆为水平杆，竖直载荷P 和尺寸a 、b 均为已知，各杆自重均不计。

当结构处于平衡时，求载荷P 的作用点与B 点之间的水平距离x 的值。

解：注意到： 杆HK 为“二力杆”。

以“整 体”为研究对象，受力分析如“图（i ）”所示。

()∑=0F M A： ()04=+⋅-⋅b x P b F D ， 得P b bx F D ⋅+=4∑=0yF ： 0=-+P F F D Ay ， 得P b xb F P F D Ay ⋅-=-=43∑=0xF：0=+Ax F ， 得 0=Ax F再以“AB 杆”为研究对象，受力分析如“图（ii ）”所示。

由 ③ 可知，此时A 处的约束力只有AyF 。

第三题图()∑=0F M B：2=⋅-⋅b F a F Ay HK ， 得Ay HK F a b F 2=将 ② 代入， 得P a xb F HK ⋅-=83再以“CD 杆”为研究对象，受力分析如“图（iii ）”所示。

()∑=0F M C： 03=⋅-⋅a F b F HK D ， 得D HK F a bF 3=将 ① 代入， 得P a xb F HK ⋅+=12由 ④、⑤ ，得 P a x b P a x b ⋅+=⋅-1283解得bx 57=A DF 图（ii ）AF2杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F1和F2作用在销钉C 上，F1=445 N ，F2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N =⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

F 1F3.水平力F 作用在刚架的B 点，如图所示。

静力学部分小题：简单计算题考点：力偶系平衡问题1. 如图所示平面结构，已知杆AB 和杆CD 的重量不计，且DC 杆在C 点靠在光滑的AB杆上，若作用在杆AB 上的力偶的力偶矩为1m ，则欲使系统保持平衡，求作用在CD 杆上的力偶的力偶矩2m 的大小。

2. 在图示平面结构中，杆AC 和杆BD 为无重杆，在C 处作用一力偶矩为M 的力偶，求A和B 处的约束反力。

3. 如图所示，在三铰拱结构的两半拱上，作用两个等值、反向、力偶矩为M 的力偶，如两半拱的重量不计，试求A 、B 处的约束力。

4. 如图所示平面结构，杆AC 、BC 为无重杆，其上作用两个等值、反向、力偶矩为M 的力偶，试求A 、B 处的约束反力。

A605. 外伸梁AC 的尺寸及受力如图所示，已知Q =Q ’=1200N ，M =400m N ，a =1m ，梁的自重不计，求支座A 、B 的约束反力。

6.A 、C 的约束反力。

7. 如图所示平面结构，一力偶矩为M 的力偶作用在直角曲杆ADB 上。

不计杆重，求支座A 、B 对杆的约束反力。

8. 如图所示平面结构，一力偶矩为M 的力偶作用在直角曲杆ADB 上。

不计杆重，求支座A 、B 对杆的约束反力。

9. 在图示平面结构中，已知力偶矩为M ，AC =L，构件自重不计，求支座A ，C 处的约束反力。

Q ＇10. 如图所示，已知P =P ’=3.96KN ，构件自重不计，求支座A 、C 的约束反力（AC =1m ）。

11. 如图所示平面刚架，已知：123kN m 1kN m m m =⋅=⋅， ,转向如图。

a ＝1m ，试求图示刚架A 及B 处的约束反力。

12. 平面四连杆机构，在图示位置平衡，3090αβ＝，＝。

已知：O 1A =6a ，O 2B =8a 。

求此时12/m m 的值。

13. 在图示平面结构中，已知力偶矩M =4KN m ，AC =1m ，构件自重不计，求支座A ，C 的约束反力。

14. 如图所示平面刚架，已知：40kN m M =⋅,F =10kN,q =5kN/m 。

一、判断题（共30分，每道3分）1.两个大小相等、方向相同的力分别作用于同一物体时，它们对物体产生的效应相同。

（）2.凡合力都比分力大。

（）3.汇交的三个力是平衡力。

（）4.当平面汇交力系平衡时，选择几个投影轴就能列出几个独立的平衡方程。

（）5.两个力F1，F2在同一轴上的投影相等，则这两个力一定相等。

（）6.在平面中任意两个力都可以简化为一个合力。

（）7.平面力偶的大小与钜心点的位置有关。

（）8.当平面任意力系向某点简化结果为力偶时，如果再向另一点简化，则其结果是一样的。

（）9.作用于刚体上的平面任意力学，若其力多边形自行封闭，则此刚体平衡。

（）10.如果某平面任意力系由多个力偶和一个力组成，该力系一定不是平衡力系。

（）二、填空题（共20分，每道4分）1.图示三饺刚架受力图，则A支座反力的大小为，B支座反力的大小为。

2.图示结构受力偶M=10kN∙m图，若a=1m，各杆不计自重，则固定铰支座D的反力的大小为，方向为。

3.不计重量的直角杆CDA和T字形杆DBE在D处铰接，如图所示。

若系统受力作用，则B支座约束力的大小为，方向为。

4. 直角弯杆ABCD 与直杆DE 及EC 铰接如图，作用在DE 杆上力偶矩M =40kN ∙m ，不计杆重和摩擦，尺寸如图。

则支座A 的约束反力大小为 ，B 处的约束反力大小为 。

5. 图示AB 杆，不计自重，在5个力作用下处于平衡，则作用于B 点的4个力的合力F R的大小为，方向沿着。

三、 计算题（共50分）1. 四连杆机构OABO 1在图示位置平衡，已知OA=0.4m ，O 1B=0.6m ，AB 处于水平位置。

作用在曲柄OA 上的力偶矩M 1=10kN ∙m ，不计自重，求力偶M 2的大小及连杆AB 所受的力。

（10分）2. 图示滑道连杆机构，在滑道连杆上作用水平力F 。

已知曲柄OA=r ，滑道倾角为β，曲柄OA 与水平夹角θ，机构重量和各处摩擦力不计。

试求当机构平衡时，作用在曲柄OA 上的力偶M 的大小。

第一章静力学公理和物体的受力分析一、选择题1、三力平衡定理是 _______ 。

① 共面不平行的三个力互相平衡必汇交于一点； ② 共面三力假设平衡，必汇交于一点； ③ 三力汇交于一点，那么这三个力必互相平衡。

2、 三力平衡汇交定理所给的条件是 _____ 。

① 汇交力系平衡的充要条件； ② 平面汇交力系平衡的充要条件； ③ 不平行的三个力平衡的必要条件； ④ 不平行的三个力平衡的充分条件；3、 图示系统只受F 作用而平衡。

欲使A 支座约束力的作用线 与AE 成30°角，那么斜面的倾角应为 ________ 。

①0° ②30° ③45°④60°② 一对平衡的力或一个力偶； ③ 一对平衡的力或一个力和一个力偶; ④ 作用力和反作用力或一个力偶。

、填空题1、 力F 沿直线AE 作用，其中一个分力的作用线与AE 成 30。

角，假设欲使另一个分力的大小在所有分力中为最小，那么此 二分力间的夹角为 ________________ 度。

2、 ________________________________________________ 作用在刚体上的两个力等效的条件是 __________________________ _____________ 。

3、 将力F 沿X 、Y 方向分解，F= 100N, F 在X 轴上的 投影为86.6N,而沿X 方向的分力的大小为 115.47N,那么F 的Y 的方向分量与X 轴的夹角 为 _______ , F 在Y 轴上的投影为_______ 。

4、假设不计各物体重量，试分别画出各构杆和构造整体的受力图。

条件，那么该二力可能是 ______ 。

①作用力和反作用或是一对平衡的力;亠F第二章平面汇交力系和平面力偶系、选择题1、R 、F2、F3、F 4为作用于刚体上的平面共点力系，其 ③一定不通过A 点。

2、汇交于O 点的平面汇交力系，其平衡方程式可表示为二力 矩形式。

静力学试题及答案一、选择题1. 静力学中，力的平衡条件是什么？A. 力的大小相等B. 力的方向相反C. 力的大小相等，方向相反D. 力的大小和方向都相等答案：C2. 以下哪个不是静力学的基本概念？A. 力的合成B. 力的分解C. 力的平衡D. 力的守恒答案：D二、填空题1. 在静力学中，当一个物体处于________时，我们称其为平衡状态。

答案：静止或匀速直线运动2. 根据牛顿第一定律，物体在没有外力作用下，将保持________状态。

答案：静止或匀速直线运动三、简答题1. 简述牛顿第三定律的内容及其在静力学中的应用。

答案：牛顿第三定律指出，作用力和反作用力大小相等，方向相反，作用在两个不同的物体上。

在静力学中，这一定律用于分析物体间的相互作用，确保系统的力平衡。

2. 解释什么是静摩擦力，并说明其在物体保持静止状态时的作用。

答案：静摩擦力是阻止物体滑动的力，其大小与引起滑动的外力相等，但方向相反。

在物体保持静止状态时，静摩擦力与外力平衡，防止物体发生运动。

四、计算题1. 一个质量为10 kg的物体，受到水平方向上的两个力F1和F2的作用，F1 = 50 N，F2 = 30 N，求物体受到的合力。

答案：首先确定两个力的方向，如果F1和F2方向相反，则合力F = F1 - F2 = 50 N - 30 N = 20 N；如果F1和F2方向相同，则合力F = F1 + F2 = 50 N + 30 N = 80 N。

2. 一个斜面上的物体质量为20 kg，斜面与水平面的夹角为30°，求物体受到的重力分量在斜面方向上的分力。

答案：物体受到的重力G = m * g = 20 kg * 9.8 m/s² = 196 N。

在斜面方向上的分力 F = G * sin(θ) = 196 N * sin(30°) = 98 N。

五、分析题1. 一个均匀的直杆，长度为L，固定在水平面上的A点，B点自由悬挂，求直杆的平衡条件。

工程力学——静力学部分习题 第一章 静力学公理与物体的受力分析一、判断题1．力是滑动矢量，可沿作用线移动。

（ ） 2．凡矢量都可用平行四边形法则合成。

（ ） 3．凡是在二力作用下的约束成为二力构件。

（ ） 4．两端用光滑铰链连接的构件是二力构件。

（ ） 5．凡是合力都比分力大。

（ ） 6．刚体的平衡条件是变形体平衡的必要条件，而非充分条件。

（ ） 7．若作用在刚体上的三个力的作用线汇交于一点，则该刚体必处于平衡状态。

（ ） 二、填空题1．作用力与反作用力大小 ，方向 ，作用在 。

2．作用在同一刚体上的两个力使刚体平衡的充要条件是这两个力 ， ， 。

3．在力的平行四边形中，合力位于 。

三、选择题1．在下述公理、法则、定理中，只适用于刚体的有（ ）。

A ．二力平衡公理B 力的平行四边形法则C ．加减平衡力系原理D 力的可传性E 作用与反作用定律2．图示受力分析中，G 是地球对物体A 的引力，T 是绳子受到的拉力，则作用力与反作用力指的是（ ）。

A T ′与GB T 与GC G 与G ′D T ′与G ′3．作用在一个刚体上的两个力F A 、F B ，若满足F A ＝－F B 的条件，则该二力可能是（ ）。

A 作用力与反作用力或一对平衡力 B 一对平衡力或一个力偶 C 一对平衡力或一个力或一个力偶 D 作用力与反作用力或一个力偶 四、作图题1．试画出下列各物体的受力图。

各接触处都是光滑的。

（a ） （b）2． 试画出图示系统中系统及各构件的受力图。

假设各接触处都是光滑的，图中未画出重力的构件其自重均不考虑。

（c ）ABPo30（d ）（f ）（e ）（a ）A BP 2P 1（b）第二章 平面汇交力系与平面力偶系一、判断题1. 两个力F 1、F 2在同一轴上的投影相等，则这两个力大小一定相等。

（ ）2. 两个力F 1、F 2大小相等，则它们在同一轴上的投影大小相同。

（ ）3. 力在某投影轴方向的分力总是与该力在该轴上的投影大小相同。