2017-2018学年上海市七宝中学高二下学期数学期末考试试卷(含答案)

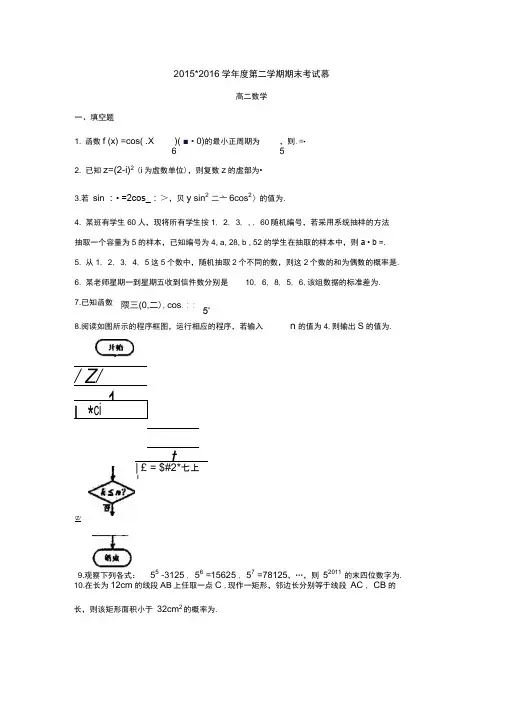
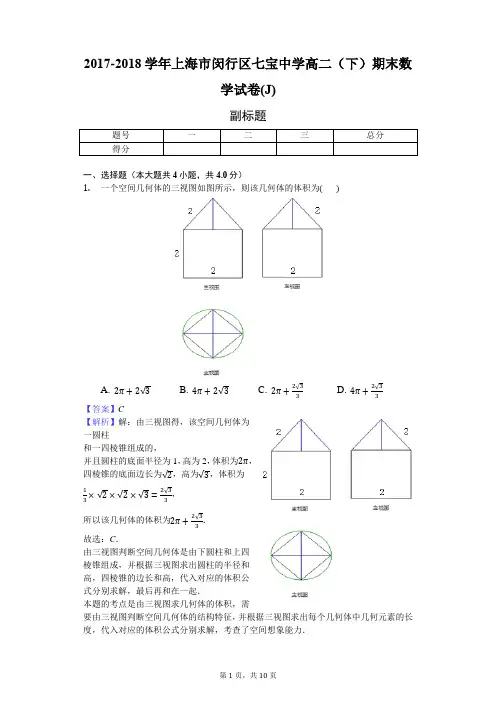
2018-2019学年上海市闵行区七宝中学高二（下）期末数学试卷一、单选题（本大题共4小题，共20.0分）1. 设x 、y 满足线性约束条件{x ≤2y ≤2x +y ≥2，则x +2y 的取值范围是( )A. [2,6]B. [2,5]C. [3,6]D. [3,5]2. 某中学高二年级的一个研究性学习小组拟完成下列两项调查：①从某社区430户高收入家庭，980户中等收入家庭，290户低收入家庭中任意选出170户调查社会购买力的某项指标；②从本年级12名体育特长生中随机选出5人调查其学习负担情况； 则该研究性学习小组宜采用的抽样方法分别是( )A. ①用系统抽样，②用随机抽样B. ①用系统抽样，②用分层抽样C. ①用分层抽样，②用系统抽样D. ①用分层抽样，②用简单随机抽样3. 12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排(这样就成为前排6人，后排6人)，若其他人的相对顺序不变，则不同调整方法的种数是( )A. C 82A 32B. C 82A 66C. C 82A 62D. C 82A 524. 如图，E 、F 分别为棱长为1的正方体的棱A 1B 1、B 1C 1的中点，点G 、H 分别为面对角线AC 和棱AA 1上的动点，则下列关于四面体E −FGH 的体积正确的是( )A. 该四面体体积有最大值，也有最小值B. 该四面体体积为定值C. 该四面体体积只有最小值D. 该四面体体积只有最大值二、单空题（本大题共12小题，共60.0分）5. 将参数方程{x =1+2ty =2−t(t ∈R,t 为参数)化为普通方程______．6. 已知椭圆x 29+y 24=1，直线x +2y +18=0，则椭圆上点到这条直线的最短距离是______．7. −1+3C 111−9C 112+27C 113−⋯−310C 1110+311除以5的余数是______．8. (文)如图为某几何体的三视图，则其侧面积为______cm 2．9. (文)甲、乙、丙、丁4名同学被随机地分到A 、B 、C 三个社区参加社会实践，要求每个社区至少有一名同学．则甲、乙两人被分在同一个社区的概率是______． 10. 侧棱长为2√3的正三棱锥V −ABC 中，∠AVB =∠BVC =∠CVA =40°，过点A 作截面AEF ，则截面△AEF 周长的最小值为 ．11. 长方体ABCD −A 1B 1C 1D 1内接于球O ，且AB =BC =2，AA 1=2√2，则A 、B 两点之间的球面距离为______．12. 从装有n +1个球(其中n 个白球，1个黑球)的口袋中取出m 个球(0<m ≤n,m ，n ∈N)，共有C n+1m 种取法．在这C n+1m种取法中，可以分成两类：一类是取出的m 个球全部为白球，另一类是取出m −1个白球，1个黑球，共有C 10⋅C n m +C 11⋅C n m−1=C n+1m ，即有等式：C n m +C n m−1=C n+1m 成立．试根据上述思想化简下列式子：C k 0C n m +C k 1⋅C n m−1+C k 2⋅C n m−2+⋯+C k k ⋅C n m−k =______ .(1≤k <m ≤n,k ，m ，m ∈N)． 13. 已知平行六面体ABCD −A′B′C′D′中，AB =4，AD =3，AA′=5，∠BAD =90°，∠BAA′=∠DAA′=60°，则AC′的长为______ ．14. 某几何体的一条线段为√7，在该几何体的正视图中，这条线段的投影是长为√6的线段，在该几何体的侧视图与俯视图中，这条线段的投影分别是长为a 和b 的线段，则a +b 的最大值为______．15. 数列{a n }共有13项，a 1=0，a 13=4，且|a k+1−a k |=1，x =1，2…12，满足这种条件不同的数列个数为______．16.如图，在底面半径和高均为1的圆锥中，AB、CD是底面圆O的两条互相垂直的直径，E是母线PB的中点，已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分，则该抛物线的焦点到其准线的距离为______．三、解答题（本大题共5小题，共60.0分）17.有8名学生排成一排，求分别满足下列条件的排法种数，要求列式并给出计算结果．(1)甲不在两端；(2)甲、乙相邻；(3)甲、乙、丙三人两两不得相邻；(4)甲不在排头，乙不在排尾．)12的展开式中．18.在二项式(2x3+1x(1)求该二项展开式中所有项的系数和的值；(2)求该二项展开式中含x4项的系数；(3)求该二项展开式中系数最大的项．19.如图，在直三棱柱ABC−A1B1C1中，CC1=AC=BC，∠ACB=90°，P是AA1的中点，Q是AB的中点．(1)求异面直线PQ与B1C所成角的大小；(2)若直三棱柱ABC−A1B1C1的体积为1，求四棱锥C−2BAPB1的体积．20.圆锥的轴截面为等腰直角三角形SAB，Q为底面圆周上一点．(Ⅰ)如果BQ的中点为C，OH⊥SC，求证：OH⊥平面SBQ；(Ⅱ)如果∠AOQ=60°，QB=2√3，求此圆锥的体积；(Ⅲ)如果二面角A−SB−Q的大小为arctan√6，求∠AOQ的3大小．21. (1)集合Q ={x|x =(x 1,x 2,…,x n )，x i =0或1}，对于任意x ∈Q ，定义f(x)=∑x i n i=1，对任意k ∈{0,1，2，…，n}，定义A k ={x|f(x)=k,x ∈Q}，记a k 为集合A k 的元素个数，求a 1+2a 2+⋯+na n 的值；(2)在等差数列{a n }和等比数列{b n }中，a 1=b 1=2，a 2=b 2=2+b ，是否存在正整数b ，使得数列{b n }的所有项都在数列{a n }中，若存在，求出所有的b ，若不存在，说明理由；(3)已知当|x|<12时，有11+2x =1−2x +4x 2−⋯+(−2x)n +⋯，根据此信息，若对任意|x|<12，都有x(1−x 3)(1+2x)=a 0+a 1x +a 2x 2+⋯+a n x n+⋯，求a 10的值．答案和解析1.【答案】A【解析】解：约束条件{x≤2y≤2x+y≥2对应的可行域如下图：由图可知：当x=2，y=2时，目标函数Z 有最大值Zmax=6，当x=2，y=0时，目标函数Z有最小值Zmax=2，则x+2y的取值范围是：[2,6]，故选：A．本题考查的知识点是线性规划，处理的思路为：根据已知的约束条件{x≤2y≤2x+y≥2画出满足约束条件的可行域，再用角点法，求出目标函数的最大值．用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组(方程组)寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．2.【答案】D【解析】【分析】本题主要考查随机抽样的应用，利用三种抽样的定义是解决本题的关键，比较基础．分别根据分层抽样，系统抽样和简单抽样的定义进行判断即可．【解答】解：①由于三种收入的家庭差异比使用较明显，故①应用分层抽样．②由于12名特长生人数比较少，可以使用简单随机抽样即可，故选：D．3.【答案】C【解析】解：从后排8人中选2人共C 82=28种选法．这2人插入前排4人中，且保证前排人的顺序不变，则先从4人中的5个空挡插入一人，有5种插法；余下的一人则要插入前排5人的空挡，有6种插法， 故不同调整方法的种数是28×5×6=840， 故选C ．分三步完成：①先从后排8人中选2人共C 82种选法．②把这2人插入前排4人中，且保证前排人的顺序不变，则先从4人中的5个空挡插入一人，有5种插法．③余下的一人则要插入前排5人的空挡，有6种插法，再根据分步计数原理求得结果． 本题主要考查排列、组合以及简单计数原理的应用，属于中档题．4.【答案】D【解析】解：∵E 、F 分别为棱长为1的正方体的棱A 1B 1、B 1C 1的中点， ∴EF//A 1C 1，而A 1C 1//AC ， ∴EF//AC ，而G 为面对角线AC 上的动点，∴点G 到直线EF 的距离为定值则三角形EFG 的面积为定值． 此四面体体积V =S △EFG ℎ，h 为点H 到面EFG 的距离．根据直线A 1A 与面EFG 相交，交点为A ，当点H 在A 1处h 取最大值， H 可无限靠近A 但不能在A 处，∴此四面体体积有最大值，不存在最小值， 故选：D ．根据EF//AC ，可知点G 到直线EF 的距离为定值则三角形EFG 的面积为定值，只需研究点H 到平面EFG 的距离的取值范围即可得到四面体体积的取值范围．本题主要考查了四面体的体积，以及运动中的不变问题，同时考查了了空间想象能力和转化的思想，属于中档题．5.【答案】x +2y −5=0【解析】解：∵参数方程{x =1+2ty =2−t (t ∈R,t 为参数)， ∴普通方程为x +2y −5=0．故答案为：x+2y−5=0．参数方程消去参数能求出普通方程．本题考查普通方程的求法，考查参数方程、普通方程的互化等基础知识，考查运算求解能力，是中档题．6.【答案】13√55【解析】解：由直线l的方程与椭圆的方程可以知道，直线lx+2y+18=0与椭圆不相交，设直线m平行于直线l，则直线m的方程可以写成x+2y+k=0(1)由方程组{x29+y24=1x+2y+k=0消去x，得25y2+16ky+4k2−36=0(2)令方程(2)的根的判别式△=0，得162k2−4×25(4k2−36)=0(3)解方程(3)得k1=5或k2=−5，∴当k1=5时，直线m与椭圆交点到直线l的距离最近，此时直线m的方程为x+2y+5= 0，直线m与直线l间的距离d=√1+4=13√55，故答案为：13√55．由直线l的方程与椭圆的方程可以知道，直线l与椭圆不相交，将直线l：x+2y+18=0平移，使得其与椭圆相切，则可知切线与直线l的距离最小或最大，故设直线m平行于直线l，则直线m的方程可以写成x+2y+k=0与椭圆方程联立，利用判别式为0可求解．本题考查直线和椭圆的位置关系，解题的关键是将直线l：x+2y+18=0平移，使得其与椭圆相切，属基础题．7.【答案】3【解析】【分析】本题主要考查二项式定理的应用，整除的有关知识，属于中档题．所给的式子即(−1+3)11=2048=2045+3，显然它除以5的余数为3．【解答】解：∵−1+3C 111−9C 112+27C 113−⋯−310C 1110+311 =(−1+3)11=2048=2045+3，它除以5的余数显然为3， 故答案为：3．8.【答案】4π【解析】解：由三视图知：几何体为圆锥，且圆锥的底面直径为2，高为√15， ∴圆锥的母线长为√15+1=4，∴几何体的侧面积S =π×1×4=4π(cm 2) 故答案为：4π．几何体为圆锥，由三视图的数据可得圆锥的底面直径与高，求得其母线长，把数据代入圆锥的侧面积公式计算．本题考查了由三视图求几何体的体积，根据三视图求几何体相关几何量的数据是关键．9.【答案】16【解析】解：把甲、乙看成一个整体，与其他的2人分到A 、B 、C 三个社区，共有A 33 种不同的方法，而所有的分配方法有C 42A 33种，故甲、乙两人被分在同一个社区的概率是P =A 33C 42A 33=16，即甲、乙两人同时到同一个社区的概率是16， 故答案为：16．甲、乙两人被分在同一个社区的方法有A 33种，而所有的分配方法有C 42A 33种，由此求得甲、乙两人被分在同一个社区的概率．本题考查求等可能事件的概率，得到甲、乙两人被分在同一个社区的方法有A 33种，是解题的关键．10.【答案】6【解析】 【分析】本题主要考查余弦定理的应用，棱锥的结构特征，利用棱锥的侧面展开图研究几条线段和的最小值问题，是一种重要的解题方法．沿着侧棱VA把正三棱锥V−ABC展开在一个平面内，如图，则AA′即为截面△AEF周长的最小值，且∠AVA′=3×40°=120°，在△VAA′中，由余弦定理可得AA′的值．【解答】解：如图所示：沿着侧棱VA把正三棱锥V−ABC展开在一个平面内，如图(2)，则AA′即为截面△AEF周长的最小值，且∠AVA′=3×40°=120°．△VAA′中，由余弦定理可得AA′=√VA2+VA′2−2VA⋅VA′⋅cos∠AVA′=√12+12−2×12cos120°=6，故答案为6．11.【答案】2π3【解析】【分析】此题考查了长方体外接球问题，属于基础题．利用长方体外接球直径为其体对角线长求得外接球半径，及AB所对球心角，得解．【解答】解：由AB=BC=2，AA1=2√2，得AC1=BD1=4，∴△ABO为正三角形，∠AOB=π3，∴A，B两点间的球面距离为2×π3=2π3，故答案为：2π3．12.【答案】C n+k m【解析】解：在C n m +C k 1⋅C n m−1+C k 2⋅C n m−2+⋯+C k k ⋅C nm−k 中， 从第一项到最后一项分别表示：从装有n 个白球，k 个黑球的袋子里，取出m 个球的所有情况取法总数的和，故答案应为：从从装有n +k 球中取出m 个球的不同取法数C n+k m故选C n+k m从装有n +1个球(其中n 个白球，1个黑球)的口袋中取出m 个球(0<m ≤n,m ，n ∈N)，共有C n+1m 种取法．在这C n+1m 种取法中，可以分成两类：一类是取出的m 个球全部为白球，另一类是，取出1个黑球，m −1个白球，则C n m +C n m−1=C n+1m 根据上述思想，在式子：C n m +C k 1⋅C n m−1+C k 2⋅C n m−2+⋯+C k k ⋅C nm−k 中，从第一项到最后一项分别表示：从装有n 个白球，k 个黑球的袋子里，取出m 个球的所有情况取法总数的和，故答案应为：从从装有n +k 球中取出m 个球的不同取法数，根据排列组合公式，易得答案．这个题结合考查了推理和排列组合，处理本题的关键是熟练掌握排列组合公式，明白每一项所表示的含义，再结合已知条件进行分析，最后给出正确的答案．13.【答案】√85【解析】解：由题意可得，AC′⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +CC′⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ +AA′⃗⃗⃗⃗⃗⃗ ，所以|AC′⃗⃗⃗⃗⃗⃗ |2=|AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ +AA′⃗⃗⃗⃗⃗⃗ |2=AB ⃗⃗⃗⃗⃗ 2+AD ⃗⃗⃗⃗⃗⃗ 2+AA′⃗⃗⃗⃗⃗⃗ 2+2(AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ⋅AA′⃗⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ ⋅AA′⃗⃗⃗⃗⃗⃗ )=42+32+52+2×(4×3×0+4×5×12+3×5×12)=85，所以AC′的长为√85．故答案为：√85．将所求解的长度转化为空间向量AC′⃗⃗⃗⃗⃗⃗ 的模进行求解，然后利用空间向量基本定理得到AC′⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +CC′⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ +AA′⃗⃗⃗⃗⃗⃗ ，然后求解模即可．本题考查了空间向量在立体几何中的应用，涉及了空间向量基本定理的应用，空间向量数量积的定义，空间向量模的运算性质，解题的关键是确定基底，考查了逻辑推理能力与化简运算能力，属于中档题．14.【答案】4【解析】解：由棱和它在三视图中的投影扩展为长方体，三视图中的三个投影，是三个面对角线，则设长方体的三度：x 、y 、z ，所以x 2+y 2+z 2=7，x 2+y 2=a 2，y 2+z 2=b 2，x 2+z 2=6可得a 2+b 2=8∵(a +b)2≤2(a 2+b 2)a +b ≤4∴a +b 的最大值为：4故答案为：4由棱和它在三视图中的投影扩展为长方体，三视图中的三个投影，是三个面对角线，设出三度，利用勾股定理，基本不等式求出最大值．本题考查三视图，几何体的结构特征，考查空间想象能力，基本不等式的应用，是中档题．15.【答案】495【解析】解：∵|a k+1−a k |=1，∴a k+1−a k =1或a k+1−a k =−1，设有x 个1，则有12−x 个−1∴a 13−a 1=(a 13−a 11)+((a 12−a 11)+(a 11−a 10)+⋯+(a 2−a 1)∴4=x+(12−x)⋅(−1)∴x=8∴这样的数列个数有C128=495，故答案为：495根据题意，先确定数列中1的个数，再利用组合知识，即可得到结论．本题考查数列知识，考查组合知识的运用，确定数列中1的个数是关键．16.【答案】√22【解析】解：如图所示，过点E作EG⊥AB，垂足为F．∵E是母线PB的中点，圆锥的底面半径和高均为1，∴OF=EF=12，∴OE=√22．在平面CED内建立直角坐标系．设抛物线的方程为y2=2px(p>0)，C(√22,1)，∴1=2×√22p，解得p=√22．∴该抛物线的焦点到其准线的距离为√22．故答案为：√22．如图所示，过点E作EF⊥AB，垂足为F.由于E是母线PB的中点，圆锥的底面半径和高均为1，可得OF=EF=12.OE=√22.在平面CED内建立直角坐标系．设抛物线的方程为y2=2px(p>0)，F为抛物线的焦点．可得C(√22,1)，代入解出p即可．本题考查了圆锥的性质、抛物线的标准方程，考查了转变角度解决问题的能力，考查了推理能力与计算能力，是中档题．17.【答案】解：(1)假设8个人分别对应8个空位，甲不站在两端，有6个位置可选，则其他7人对应其他7个位置，有6A77=30240种情况，(2)把甲乙两人捆绑在一起看做一个复合元素，再和另外6人全排，故有2A77=10080种情况，(3)将甲、乙、丙三人插入到另外5人排列后所成的6个空中的3个空，故有A 55A 63=14400种情况，(4)利用间接法，故有A 88−2A 77+A 66=30960种情况．【解析】(1)假设8个人分别对应8个空位，甲不站在两端，有6个位置可选，则其他7人对应其他7个位置，由分步计数原理计算可得答案；(2)把甲乙两人捆绑在一起看做一个复合元素，再和另外6人全排；(3)将甲、乙、丙三人插入到另外5人排列后所成的6个空中的3个空；(4)利用间接法可得．本题考查排列、组合的运用，先根据已知找到突破口，再以此推出其它位置的人是解题的关键．18.【答案】解：(1)令x =1，可得该二项展开式中所有项的系数和的值为312．(2)该二项展开式中，通项公式为T r+1=C 12r ⋅212−r ⋅x 36−4r ，令36−4r =4，求得r =8，故含x 4项的系数为C 12824=7920．(3)第r +1项的系数为C 12r ⋅212−r ，由{C 12r ⋅212−r ≥C 12r−1⋅213−rC 12r ⋅212−r ≥C 12r+1⋅211−r，求得r =3， 故该二项展开式中系数最大的项为 C 123(2x 3)9(1x )3=112640x 24．【解析】(1)令x =1，可得该二项展开式中所有项的系数和的值．(2)在通项公式中，令x 的幂指数等于4，求得r 的值，可得含x 4项的系数．(3)根据{C 12r ⋅212−r ≥C 12r−1⋅213−r C 12r ⋅212−r ≥C 12r+1⋅211−r，求得r 的值，可得结论． 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于中档题．19.【答案】解：(1)以C 为坐标原点，以CA ，CB ，CC 1为X ，Y ，Z 轴正方向建立空间直角坐标系．不妨设CC 1=AC =BC =2．依题意，可得点的坐标P(2,0，1)，Q(1,1，0)，B 1(0,2，2)．于是，PQ ⃗⃗⃗⃗⃗ =(−1,1,−1)，B 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,−2,−2)．由PQ ⃗⃗⃗⃗⃗ ⋅B 1C ⃗⃗⃗⃗⃗⃗⃗ =0，则异面直线PQ 与B 1C 所成角的大小为π2．(2)连接CQ.由AC=BC，Q是AB的中点，得CQ⊥AB；由AA1⊥面ABC，CQ⊊面ABC，得CQ⊥AA1．又AA1∩AB=A，因此CQ⊥面ABB1A1由直三棱柱ABC−A1B1C1的体积为12⇒CC1=AC=BC=1.可得CQ=√22．所以，四棱锥C−BAPB1的体积为V C−BAPB1=13⋅CQ⋅S BAPB1=13⋅√22⋅[12(12+1)⋅√2]=14．【解析】(1)以C为坐标原点，以CA，CB，CC1为X，Y，Z轴正方向建立空间直角坐标系，分别求出异面直线PQ与B1C的方向向量，代入向量夹角公式，即可求出异面直线PQ与B1C所成角的大小；(2)连接CQ.由AC=BC，由已知中，Q是AB的中点，AA1⊥面ABC，我们根据等腰三角形“三线合一”的性质及线面垂直的性质，即可得到CQ⊥AB，CQ⊥AA1，进而根据线面垂直的判定定理，得到CQ⊥面ABB1A1，故CQ即为四棱锥C−BAPB1的高，求出棱锥的底面面积，代入棱锥体积公式，即可得到答案．本题考查的知识点是异面直线及其所成的角，棱锥的体积，其中(1)的关键是建立空间坐标系，将异面直线夹角问题转化为向量夹角问题，而(2)的关键是根据线面垂直的判定定理，得到CQ为棱锥的高．20.【答案】证明：(I)连接OC、AQ，因为O为AB的中点，所以OC//AQ．因为AB为圆的直径，所以∠AQB=90°，OC⊥BQ．因为SO⊥平面ABQ，所以SO⊥BQ，所以QB⊥平面SOC，OH⊥BQ.又OH⊥SC，SC∩BQ=C，所以OH⊥平面SBQ．解：(II)∵∠AOQ=60°∴∠OBQ=∠OQB=30°∵BQ=2√3∴AB=4，AQ=2，又SA⊥SB，SA=SB=2√2∴SO=OA=BO=2∴V=13π⋅OA2⋅SO=8π3．(III)作QM⊥AB于点M，∵平面SAB⊥平面ABQ且平面SAB∩平面ABQ=AB ∴QM⊥平面SAB．再作MP⊥SB于点P，连QP∴QP⊥SB∴∠MPQ为二面角A−SB−Q的平面角∴∠MPQ=arctan√63．∴MQ：MP=√6：3．设OA=OB=R，∠AOQ=α∴MQ=Rsinα，OM=Rcosα，MB=R(1+cosα)，∠SBA=45°∴MP=BP∴MP=√22MB=√22R(1+cosα)∴Rsinα：√22R(1+cosα)=√6：3．∴1+cosαsinα=√3∴cot α2=√3解得α=60°，∠AOQ=60°．【解析】(I)连接OC、AQ，由三角形中位线定理可得OC//AQ，由圆周角定理我们可得OC⊥BQ，由圆锥的几何特征，可得SO⊥BQ，进而由线面垂直的判定定理，得到QB⊥平面SOC，则OH⊥BQ，结合OH⊥SC及线面垂直的判定定理得到OH⊥平面SBQ；(Ⅱ)若∠AOQ=60°，易得∠OBQ=∠OQB=30°，又由QB=2√3，我们求出圆锥的底面半径OA长及圆锥的高SO，代入圆锥体积公式，即可得到圆锥的体积；(Ⅲ)作QM⊥AB于点M，由面面垂直的判定定理可得QM⊥平面SAB，作MP⊥SB于点P，连QP，则∠MPQ为二面角A−SB−Q的平面角，根据二面角A−SB−Q的大小为arctan√63，设OA=OB=R，∠AOQ=α，进而可求出∠AOQ的大小．本题考查的知识点是二面角的平面角及求法，圆锥的体积，直线与平面垂直的判定，其中(I)的关键是熟练掌握空间线线垂直，线面垂直的相互转化，(II)的关键是求出底面半径及高，(III)的关键是确定∠MPQ为二面角A−SB−Q的平面角．21.【答案】解：(1)由题意得集合A k.表示方程x1+x2+⋯+x n=k解的集合，由于x i=0或，∴方程x1+x2+⋯+x n=k中有k个，n−k个，从而可得到解的情况共有C n k个，∴a k=C n k．令S=a1+2a2+⋯+na n=C n1+2C n2+⋯+nC n n，∴S=nC n n+⋯+2C n2+C n1，∴2S =nC n n +nC n n−1+⋯+nC n 2+nC n 1+nC n n=nC n n +nC n n−1+⋯+nC n 2+nC n 1+nC n 0=n ⋅2n ，∴S =n ⋅2n−1，即S =nC n n +⋯+2C n 2+C n 1．(2)当b 取偶数(b =2k,k ∈N ∗)时，{b n }中所有项都是{a n }中的项．∵b 1，b 2均在数列{a n }中，当n ≥3时，b n =2(2+b 2)n−1=2(k +1)n−1=2(C n−10k n−1+C n−11k n−2+⋯+C n−1n−2k 1+C n−1n−1) =2+2k[(C n−10k n−2+C n−11k n−3+⋯+C n−1n−2+1)−1]，说明数列{b n }的第n 项是数列{a n }中的第C n−10k n−2+C n−11k n−3+⋯+C n−1n−2+1项．当b 取奇数(b =2k +1,k ∈N ∗)时，∵b n 不是整数，∴数列{b n }的所有项都不在数列{a n }中．综上，b 为正偶数．(3)当|x|<12时，有11+2x =1−2x +4x 2−⋯+(−2x)n +⋯①当|x|<12时，x 1−x 3=1+x 3+x 6+⋅x 9+⋯+(x 3)n +⋯(2)②又对任意|x|<12，都有x (1−x 3)(1+2x)=a 0+a 1x +a 2x 2+⋯+a n x n +⋯③ ∴a 10即为x 10的系数，可取①中(−2x)9、②中的1；或①中(−2x)6、②中的x 3； 或①中(−2x)3、②中的x 6；或①中的、②中的x 9；∴a 10=(−2)9+(−2)6+(−2)3+1=−455．【解析】(1)由题意得集合A k .表示方程x 1+x 2+⋯+x n =k 解的集合，由于x i =0或，即可得到集合A k 的元素个数a k ，利用倒序相加法及C n k =C nn−k ，即可得到答案； (2)假设存在b ，对b 分奇数和偶数两种情况进行讨论；(3)利用类比推理和分类计数原理可得a 10的值．本题考查了对集合新定义的理解，等比数列的控究性问题，类比推理与计数原理相结合的问题，考查了分类讨论和计算能力，属难题．。

2017—2018学年度第二学期期末教学质量检测高二理科数学第Ⅰ卷（选择题共60分）一、选择题（共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.1.已知复数满足，则（）A. B. C. D.【答案】C【解析】分析：根据复数的除法法则求解可得结果．详解：∵，∴．故选C．点睛：本题考查复数的除法运算，考查学生的运算能力，解题时根据法则求解即可，属于容易题．2.2.有一段“三段论”推理是这样的：对于可导函数，如果，那么是函数的极值点，因为函数在处的导数值，所以，是函数的极值点.以上推理中（）A. 大前提错误B. 小前提错误C. 推理形式错误D. 结论正确【答案】A【解析】分析：根据极值定义得导数为零的点不一定为极值点，得大前提错误.详解：因为根据极值定义得导数为零的点不一定为极值点，所以如果f ' (x0)=0，那么x=x0不一定是函数f(x)的极值点，即大前提错误.选A.点睛：本题考查极值定义以及三段论概念，考查对概念理解与识别能力.3.3.在回归分析中，的值越大，说明残差平方和（）A. 越小B. 越大C. 可能大也可能小D. 以上都不对【答案】A【解析】分析：根据的公式和性质，并结合残差平方和的意义可得结论．详解：用相关指数的值判断模型的拟合效果时，当的值越大时，模型的拟合效果越好，此时说明残差平方和越小；当的值越小时，模型的拟合效果越差，此时说明残差平方和越大．故选A．点睛：主要考查对回归分析的基本思想及其初步应用等知识的理解，解题的关键是熟知有关的概念和性质，并结合条件得到答案．4.4.用火柴棒摆“金鱼”，如图所示，按照上面的规律，第个“金鱼”图需要火柴棒的根数为（）A. B. C. D.【答案】C【解析】由题意得，第1个“金鱼”需要火柴棒的根数为；第2个“金鱼”需要火柴棒的根数为；第3个“金鱼”需要火柴棒的根数为，构成首项为，公差为的等差数列，所以第个“金鱼”需要火柴棒的根数为，故选C.5.5.如果函数y＝f(x)的图象如图所示，那么导函数y＝f′(x)的图象可能是( )A. B. C. D.【答案】A【解析】试题分析：由原函数图像可知函数单调性先增后减再增再减，所以导数值先正后负再正再负，只有A正确考点：函数导数与单调性及函数图像6.6.某产品的广告费用万元与销售额万元的统计数据如下表：根据以上数据可得回归直线方程，其中，据此模型预报广告费用为6万元时，销售额为65.5万元，则，的值为（）A. ，B. ，C. ，D. ，【答案】C【解析】分析：根据回归直线过样本中心和条件中给出的预测值得到关于，的方程组，解方程组可得所求．详解：由题意得，又回归方程为，由题意得，解得．故选C．点睛：线性回归方程过样本中心是一个重要的结论，利用此结论可求回归方程中的参数，也可求样本数据中的参数．根据回归方程进行预测时，得到的数值只是一个估计值，解题时要注意这一点．7.7.利用数学归纳法证明不等式的过程中，由变到时，左边增加了（）A. 1项B. 项C. 项D. 项【答案】C【解析】分析：先表示出、，通过对比观察由变到时，项数增加了多少项. 详解：因为，所以当，当，所以由变到时增加的项数为.点睛：本题考查数学归纳法的操作步骤，解决本题的关键是首先观察出分母连续的整数，当，，由此可得变化过程中左边增加了多少项，意在考查学生的基本分析、计算能力．8.8.如图，用、、三类不同的元件连接成一个系统.当正常工作且、至少有一个正常工作时，系统正常工作，已知、、正常工作的概率依次为0.9、0.8、0.8，则系统正常工作的概率为（）A. 0.960B. 0.864C. 0.720D. 0.576【答案】B【解析】试题分析：系统正常工作当①正常工作，不能正常工作，②正常工作，不能正常工作,③正常工作，因此概率.考点：独立事件的概率.9.9.设复数，若，则的概率为（）A. B. C. D.【答案】D【解析】若则，则的概率为：作出如图，则概率为直线上方与圆的公共部分的面积除以整个圆的面积，即：10.10.设函数的定义域为，若对于给定的正数，定义函数，则当函数，时，定积分的值为（）A. B. C. D.【答案】D【解析】分析：根据的定义求出的表达式，然后根据定积分的运算法则可得结论．详解：由题意可得，当时，，即．所以．故选D．点睛：解答本题时注意两点：一是根据题意得到函数的解析式是解题的关键；二是求定积分时要合理的运用定积分的运算性质，可使得计算简单易行．11.11.已知等差数列的第项是二项式展开式的常数项，则（）A. B. C. D.【答案】C【解析】试题分析：二项式展开中常数项肯定不含，所以为，所以原二项式展开中的常数项应该为，即，则，故本题的正确选项为C.考点：二项式定理.12.12.已知函数的定义域为，为的导函数，且，若，则函数的取值范围为（）A. B. C. D.【答案】B【解析】分析：根据题意求得函数的解析式，进而得到的解析式，然后根据函数的特征求得最值．详解：由，得，∴，设（为常数），∵，∴，∴，∴，∴，∴当x=0时，；当时，，故当时，，当时等号成立，此时；当时，，当时等号成立，此时．综上可得，即函数的取值范围为．故选B．点睛：解答本题时注意从所给出的条件出发，并结合导数的运算法则利用构造法求出函数的解析式；求最值时要结合函数解析式的特征，选择基本不等式求解，求解时注意应用不等式的条件，确保等号能成立．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分）13.13.已知随机变量服从正态分布，若，则等于__________．【答案】0.36【解析】.14.14.从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人，组成4人服务队，要求服务队中至少有1名女生，共有__________种不同的选法．（用数字作答）【答案】660【解析】【详解】第一类，先选女男，有种，这人选人作为队长和副队有种，故有种；第二类，先选女男，有种，这人选人作为队长和副队有种，故有种，根据分类计数原理共有种，故答案为.15.15.的展开式中的系数是__________．【答案】243【解析】分析：先得到二项式的展开式的通项，然后根据组合的方式可得到所求项的系数．详解：二项式展开式的通项为，∴展开式中的系数为.点睛：对于非二项式的问题，解题时可转化为二项式的问题处理，对于无法转化为二项式的问题，可根据组合的方式“凑”出所求的项或其系数，此时要注意考虑问题的全面性，防止漏掉部分情况．16.16.已知是奇函数，当时，，（），当时，的最小值为1，则的值等于__________．【答案】1【解析】试题分析：由于当时，的最小值为，且函数是奇函数，所以当时，有最大值为-1，从而由，所以有；故答案为：1．考点：1．函数的奇偶性；2．函数的导数与最值．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.17.复数，，若是实数，求实数的值.【答案】【解析】分析：由题意求得，进而得到的代数形式，然后根据是实数可求得实数的值．详解：.∵是实数，∴，解得或，∵，∴，∴．点睛：本题考查复数的有关概念，解题的关键是求出的代数形式，然后根据该复数的实部不为零虚部为零得到关于实数的方程可得所求，解题时不要忽视分母不为零的限制条件．18.18.某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：上年度出险次0 1 2 3 4数保费设该险种一续保人一年内出险次数与相应概率如下：一年内出险次0 1 2 3 4数概率0.30 0.15 0.20 0.20 0.10 0.05（1）求一续保人本年度的保费高于基本保费的概率；（2）已知一续保人本年度的保费高于基本保费，求其保费比基本保费高出的概率.【答案】（1）0.55（2）【解析】分析：（1）将保费高于基本保费转化为一年内的出险次数，再根据表中的概率求解即可．（2）根据条件概率并结合表中的数据求解可得结论．详解：（1）设表示事件：“一续保人本年度的保费高于基本保费”，则事件发生当且仅当一年内出险次数大于1，故．（2）设表示事件：“一续保人本年度的保费比基本保费高出”，则事件发生当且仅当一年内出险次数大于3，故．又，故，因此其保费比基本保费高出的概率为．点睛：求概率时，对于条件中含有“在……的条件下，求……发生的概率”的问题，一般为条件概率，求解时可根据条件概率的定义或利用古典概型概率求解．19.19.在数列，中，，，且，，成等差数列，，，成等比数列（）.（1）求，，及，，；（2）根据计算结果，猜想，的通项公式，并用数学归纳法证明.【答案】(1) ，，，，， (2) 猜想，，证明见解析【解析】分析：（1）根据条件中，，成等差数列，，，成等比数列及所给数据求解即可．（2）用数学归纳法证明．详解：（1）由已知条件得，，由此算出，，，，，.（2）由（1）的计算可以猜想，，下面用数学归纳法证明：①当时，由已知，可得结论成立.②假设当（且）时猜想成立，即，.则当时，，，因此当时，结论也成立.由①②知，对一切都有，成立．点睛：用数学归纳法证明问题时要严格按照数学归纳法的步骤书写，特别是对初始值的验证不可省略，有时可能要取两个(或两个以上)初始值进行验证，初始值的验证是归纳假设的基础；第二步的证明是递推的依据，证明时必须要用到归纳假设，否则就不是数学归纳法．20.20.学校为了对教师教学水平和教师管理水平进行评价，从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的，对教师管理水平给出好评的学生人数为总数的，其中对教师教学水平和教师管理水平都给出好评的有120人.（1）填写教师教学水平和教师管理水平评价的列联表：对教师管理水平不满合计对教师管理水平好评意对教师教学水平好评对教师教学水平不满意合计请问是否可以在犯错误概率不超过0.001的前提下，认为教师教学水平好评与教师管理水平好评有关？（2）若将频率视为概率，有4人参与了此次评价，设对教师教学水平和教师管理水平全好评的人数为随机变量.①求对教师教学水平和教师管理水平全好评的人数的分布列（概率用组合数算式表示）；②求的数学期望和方差.0.15 0.10 0.05 0.025 0.010 0.005 0.0012.072 2.7063.841 5.024 6.635 7.879 10.828（，其中）【答案】(1) 可以在犯错误概率不超过0.001的前提下，认为教师教学水平好评与教师管理水平好评有关. (2) ①见解析②，【解析】分析：（1）由题意得到列联表，根据列联表求得的值后，再根据临界值表可得结论．（2）①由条件得到的所有可能取值，再求出每个取值对应的概率，由此可得分布列．②由于，结合公式可得期望和方差．详解：（1）由题意可得关于教师教学水平和教师管理水平评价的列联表：对教师管理水平好评对教师管理水平不满意合计对教师教学水平好评120 60 180对教师教学水平不满意105 15 120合计225 75 300由表中数据可得，所以可以在犯错误概率不超过0.001的前提下，认为教师教学水平好评与教师管理水平好评有关.（2）①对教师教学水平和教师管理水平全好评的概率为，且的取值可以是0，1，2，3，4，其中；；；；，所以的分布列为：0 1 2 3 4②由于，则，.点睛：求离散型随机变量的均值与方差关键是确定随机变量的所有可能值，写出随机变量的分布列，正确运用均值、方差公式进行计算，对于二项分布的均值和方差可根据公式直接计算即可．21.21.已知函数，（为自然对数的底数，）.（1）判断曲线在点处的切线与曲线的公共点个数；（2）当时，若函数有两个零点，求的取值范围.【答案】(1)见解析(2)【解析】分析：（1）根据导数的几何意义可得切线方程，然后根据切线方程与联立得到的方程组的解的个数可得结论．（2）由题意求得的解析式，然后通过分离参数，并结合函数的图象可得所求的范围．详解：（1）∵，∴，∴.又，∴曲线在点处的切线方程为．由得.故，所以当，即或时，切线与曲线有两个公共点；当，即或时，切线与曲线有一个公共点；当，即时，切线与曲线没有公共点.（2）由题意得，由，得，设，则.又，所以当时，单调递减；当时，单调递增．所以.又，，结合函数图象可得，当时，方程有两个不同的实数根，故当时，函数有两个零点．点睛：函数零点个数（方程根的个数、两函数图象公共点的个数）的判断方法：（1）结合零点存在性定理，利用函数的性质确定函数零点个数；（2）构造合适的函数，判断出函数的单调性，利用函数图象公共点的个数判断方程根的个数或函数零点个数．请考生在22～23两题中任选一题作答，如果多做，则按所做的第一题记分.22.22.在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系.已知点的直角坐标为，曲线的极坐标方程为，直线过点且与曲线相交于，两点.（1）求曲线的直角坐标方程；（2）若，求直线的直角坐标方程.【答案】(1) (2) 直线的直角坐标方程为或【解析】分析：（1）根据极坐标和直角坐标间的转化公式可得所求．（2）根据题意设出直线的参数方程，代入圆的方程后得到关于参数的二次方程，根据根与系数的关系和弦长公式可求得倾斜角的三角函数值，进而可得直线的直角坐标方程．详解：（1）由，可得，得，∴曲线的直角坐标方程为.（2）由题意设直线的参数方程为（为参数），将参数方程①代入圆的方程，得，∵直线与圆交于，两点，∴．设，两点对应的参数分别为，，则，∴，化简有，解得或，∴直线的直角坐标方程为或.点睛：利用直线参数方程中参数的几何意义解题时，要注意使用的前提条件，只有当参数的系数的平方和为1时，参数的绝对值才表示直线上的动点到定点的距离．同时解题时要注意根据系数关系的运用，合理运用整体代换可使得运算简单．23.23.已知函数的定义域为.（1）若，解不等式；（2）若，求证：.【答案】(1) (2)见解析【解析】分析：（1）由可得，然后将不等式中的绝对值去掉后解不等式可得所求．（2）结合题意运用绝对值的三角不等式证明即可．详解：（1），即，则，∴，∴不等式化为．①当时，不等式化为，解得；②当时，不等式化为，解得.综上可得．∴原不等式的解集为.（2）证明：∵，∴.又，∴.点睛：含绝对值不等式的常用解法（1）基本性质法：当a>0时，|x|＜a⇔－a＜x＜a，|x|＞a⇔x＜－a或x＞a．（2）零点分区间法：含有两个或两个以上绝对值符号的不等式，可用零点分区间法去掉绝对值符号，将其转化为与之等价的不含绝对值符号的不等式(组)求解．（3）几何法：利用绝对值的几何意义，画出数轴，将绝对值转化为数轴上两点的距离求解．（4）数形结合法：在直角坐标系中作出不等式两边所对应的两个函数的图象，利用函数图象求解．。

高二期末综合复习一一、填空题1、直线013=+-y x 的倾斜角 .2、若椭圆的长轴长为12，一个焦点是(0,2)，则椭圆的标准方程为__________________.3、经过点(1,0)A 且与直线10x y ++=平行的直线l 的方程为 ________ _.4已知()2f z i z z i +=+-，求(12)f i +的值 ___________ _.5、已知直线220310x y x y +-=-+=和的夹角是 ________ _.6、已知z 为虚数，且有||5z =，如果22z z +为实数，若z 为实系数一元二次方程20x bx c ++=的根，则此方程为______________ ____.7、已知方程 221104x y k k -=--表示双曲线，则实数k 的取值范围为________________ . 8、过点(1,2)且与圆221x y +=相切的直线的方程是 ________________ _.9、设F 为抛物线24y x =的焦点，,,A B C 为该抛物线上三点，若点(1,2)A ， ABC ∆的重心与抛物线的焦点F 重合，则BC 边所在直线方程为 ________ .10、若方程0x k +=只有一个解，则实数k 的取值范围是 __________ .11、下列五个命题：①直线l 的斜率[1,1]k ∈-，则直线l 的倾斜角的范围是；②直线:1l y kx =+与过(1,5)A -，(4,2)B -两点的直线相交，则4k ≤-或34k ≥-；③如果实数,x y 满足方程22(2)3x y -+=，那么y x ④直线1y kx =+与椭圆2215x y m+=恒有公共点，则m 的取值范围是1m ≥； ⑤方程052422=+-++m y mx y x 表示圆的充要条件是41<m 或1>m ； 正确的是_______ _____ _.12、直线320x y m ++=与直线2310x y +-=的位置关系是…………………………（ ）（A ）相交 （B ）平行 （C ）重合 （D ）由m 决定13、二次方程2330x ix --=的根的情况为…………………………( )（A ）有两个不相等的实根 （B ）有两个虚根（C ）有两个共轭虚根 （D ）有一实根和一虚根14、已知△ABC 的三个顶点是(3,4)A -、(0,3)B 、(6,0)C -，求（1） BC 边所在直线的一般式方程；（2） BC 边上的高AD 所在直线的一般式方程.15、已知：21,.(1)34,||b z i a R z z ωω=+∈=+-、若求；221z az b z z ++-+(2)若=1-i ，求a 、b 的值.16、已知双曲线1C ：2214y x -=（1）求与双曲线1C 有相同的焦点，且过点P 的双曲线2C 的标准方程；（2）直线l ：y x m =+分别交双曲线1C 的两条渐近线于A 、B 两点。

2017-18学年高二年级第二学期期末考试数学试卷（理数）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．考试时间120分钟，满分150分．第I 卷（选择题，共60分）注意事项：１．答第I 卷前，考生务必将自己的姓名、准考证号、考场号、座号、考试科目涂写在答题卡上． ２．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．不能答在试题卷上．一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合{}1,0=A ，{}A y A x y x z z B ∈∈+==,,|，则集合B 的子集个数为（ ） A .3 B .4 C . 7 D .8 2．若322->m x 是41<<-x 的必要不充分条件，则实数m 的取值范围是（ ）A .[]3,3-B .(][)+∞-∞-,33,C . (][)+∞-∞-,11,D .[]1,1-3．命题“[)+∞-∈∀,2x ，13≥+x ”的否定为( )A .[),,20+∞-∈∃x 130<+xB .[),,20+∞-∈∃x 130≥+xC .[)+∞-∈∀,2x ，13<+xD .()2,-∞-∈∀x ，13≥+x4．已知函数()x f 在()+∞∞-,单调递减，且为奇函数，若()11-=f ，则满足()121≤-≤-x f 的x 的取值范围是( ）A .[]2,2-B .[]1,1-C .[]4,0D .[]3,15．已知函数()xx f 5=，()x ax x g -=2，若()[]11=g f ，则=a ( )A .1B .2C .3D .1-6．已知函数()⎩⎨⎧>+≤+-=2,log 3,2,6x x x x x f a ，()1,0≠>a a 且的值域是[)+∞,4，则实数a 的取值范围是( )A .[]1,1-B .(]2,1C .[]4,0D .[]3,17．已知函数()ax f x x -+=212 是奇函数，则使()3>x f 成立x 的取值范围是 ( )A .()1,-∞-B .()0,1-C . ()1,0D .()+∞,18．若0>>b a ，10<<c ，则 ( )A .c c b a log log <B .b a c c log log <C .c c b a <D .a b c c > 9．已知函数()12-=-mx x f 为偶函数，记()3log 5.0f a = ，()5log 2f b = ，()m f c 2=，则c b a ,,的大小关系为 ( ) A .c b a << B .b c a << C . b a c << D .a c b <<10．已知函数()34213123-+-=x mx x x f 在区间[]2,1上是增函数，则实数m 的取值范围是（ ）A .[]5,4B .[]4,2C . (][)+∞-∞-,11,D .(]4,∞- 11．已知函数()|1|23,0,21,0x x f x x x x -⎧>=⎨--+≤⎩若关于x 的方程()[]()()012=--+a x f a x f 有7个不等实根，则实数a 的取值范围是( )A .()1,2-B .[]4,2C . ()1,2--D .(]4,∞-12. 已知函数()a x x f ++-=13，⎥⎦⎤⎢⎣⎡∈e ex ,1 与()x x g ln 3=的图象上存在关于x 轴对称的点，则实数a 的取值范围是( )A .[]4,03-eB .⎥⎦⎤⎢⎣⎡+21,03e C . ⎥⎦⎤⎢⎣⎡-+4,2133e eD .[)+∞-,43e第II 卷（非选择题，共90分）注意事项：1.答题前将密封线内的项目及座号填写清楚；2.考生做答时，用黑色签字笔将答案答在答题卷上，答在试题卷上的答案无效．二、填空题（本大题共4小题，每小题5分，共20分 13．已知函数()()2'11f x f x x =++，则()=⎰1dx x f .14．函数()()x x f cos sin lg =的定义域为_______________． 15．若()02222222≥++---x x xx a 在区间[]2,1上恒成立，则实数a 的取值范围是 ______．16．设()'f x 是奇函数()x f 的导函数，()02=-f ，当0>x 时，()()'0xf x f x ->，则使()0>x f 成立的x 的取值范围是 .三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） （一）必考题：共60分 17．(本小题满分12分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,且ab c b a 3222+=+.（1）求角C 的值；（2）若ABC ∆为锐角三角形,且1=c ,求b a -3的取值范围. 18．(本小题满分12分)（单位：（1）根据频数分布表，求该产品尺寸落在的概率；（2）求这50件产品尺寸的样本平均数x ；（3）根据频率分布对应的直方图，可以认为这种产品尺寸z 服从正态分布2(,)N μσ；其中μ近似为样本平均值x ，2σ近似为样本方差2S ，经计算得222.37S =，利用正态分布，求(27.43)P z ≥．19.(本小题满分12分）如图，三棱柱111C B A ABC -中，CB AC =，1AA AB =，0160=∠BAA（1）证明：C A AB 1⊥；（2）若平面⊥ABC 平面B B AA 11，CB AB =，求直线C A 1与平面C C BB 11所成角的正弦值． 20. (本小题满分12分)已知三点()1,2-A ，()1,2B ，()0,0O ，曲线C 上任意一点()y x M ,满足||()M A M B O M O A O B+=++． （1） 求C 的方程；（2） 动点()00,y x Q ()220<<-x 在曲线C 上，l 是曲线C 在Q 处的切线．问：是否存在定点()t P ,0()0<t 使得l 与PB PA ,都相交，交点分别为E D ,，且ABQ ∆与PDE ∆的面积之比为常数？若存在，求t 的值；若不存在，说明理由． 21.(本小题满分12分）()x x f ln =，()xe x g =．1）求函数()x x f y -=的单调区间；2）求证：函数()x f y =和()x g y=在公共定义域内，()()2>-x f x g 恒成立；3）若存在两个不同的实数1x ，2x ，满足()()a x x f x x f ==2211，求证：1221>exx ． （二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，则按所作第一题计分.22.(本小题满分10分)在直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系。

2018年上海中学高二下期末数学试卷一、填空题（36分）：1. 关于x 的方程222424x x C C =的解为_________. 【答案】0或2或4【解析】【分析】因为222424x x C C =，所以：22x x =或2224x x +=，解方程可得． 【详解】解：因为222424x x C C =， 所以：22x x =或2224x x +=，解得：0x =，2x =，4x =，6x =-（舍）故答案为：0或2或4【点睛】本题考查了组合及组合数公式．属于基础题．2. 从总体中抽取一个样本是5，6，7，8，9，则总体方差的估计值是____________.【答案】2【解析】【分析】先求出样本平均数，由此能求出样本方差，由此能求出总体方差的估计值．【详解】解：从总体中抽取一个样本是5，6，7，8，9， 样本平均数为1(56789)75x =++++=， ∴样本方差2222221[(57)(67)(77)(87)(97)]25S =-+-+-+-+-=， ∴总体方差的估计值是2．故答案为：2．【点睛】本题考查总体方差的估计值的求法，考查平均数、总体方差等基础知识，考查运算求解能力，属于基础题．3. 5(31)x -的展开式中，设各项的系数和为a ，各项的二项式系数和为b ，则a b=________. 【答案】1【解析】【分析】分别求得各项系数和a 与各项的二项式系数和b ，从而求得a b的值． 【详解】解：在5(31)x -的展开式中，令1x =可得设各项的系数和为5232a ==，而各项的二项式系数和为5232b ==， ∴1a b=， 故答案为：1．【点睛】本题主要考查二项式定理的应用，注意各项系数和与各项的二项式系数和的区别，属于基础题． 4. 从长度为2、3、5、6的四条线段中任选三条，能构成三角形的概率为_______. 【答案】12【解析】试题分析：这是的道古典概率题，其基本事件有()()()()2,3,5,2,3,6,2,5,6,3,5,6共4个，由于是任意选取的，所以每个基本事件发生的可能性是相等的，记事件A 为“所选三条线段能构成三角形”，则事件A 包含()()2,5,6,3,5,62个基本事件，根据概率公式得：()2142P A ==． 考点：古典概率的计算5. 从编号为0，1，2，…，79的80件产品中，采用系统抽样的方法抽取容量是5的样本，若编号为28的产品在样本中，则该样本中产品的最大编号为___【答案】76【解析】【分析】确定系统抽样间隔16k =，根据样本中含编号为28的产品，即可求解，得到答案． 【详解】由系统抽样知，抽样间隔80165k ==， 因为样本中含编号为28的产品，则与之相邻的产品编号为12和44，故所取出的5个编号依次为12，28，44，60，76，即最大编号为76．【点睛】本题主要考查了系统抽样的应用，其中解答中熟记系统抽样的方法，确定好抽样的间隔是解答的关键，着重考查了运算与求解能力，属于基础题．6. 如果三个球的表面积之比是1:2:3，那么它们的体积之比是__________．【答案】1:【解析】∵三个球的表面积之比是1:2:3，∴三个球的半径之比是∴三个球的体积之比是1:7. 北纬45︒圈上有A ，B 两点，该纬度圈上劣弧AB R （R 为地球半径），则A ，B 两点的球面距离为________. 【答案】3R π 【解析】【分析】先求出北纬45︒圈所在圆的半径，是A 、B 两地在北纬45︒圈上对应的圆心角，得到线段AB 的长，设地球的中心为O ，解三角形求出AOB ∠的大小，利用弧长公式求A 、B 这两地的球面距离．【详解】解：北纬45︒圈所在圆的半径为2R (R R 为地球半径），∴(R θθ=是A 、B 两地在北纬45︒圈上对应的圆心角）， 故2πθ=，∴线段AB R =，3AOB π∴∠=，A ∴、B 这两地的球面距离是3R π， 故答案为：3R π． 【点睛】本题考查球的有关经纬度知识，球面距离，弧长公式，考查空间想象能力，逻辑思维能力，属于基础题．8. 一个口袋中装有2个白球和3个红球，每次从袋中摸出两个球，若摸出的两个球颜色相同为中奖，否则为不中奖，则中奖的概率为_________． 【答案】25【解析】试题分析：口袋中五个球分别记为1,2,,,a b c 从中摸出两球的方法有：1,2;1,;1,;1,;2,;2,;2,;,;,;,a b c a b c a b a c b c 共10种，其中颜色相同的有1,2;,;,;,a b a c b c 共四种，有古典概率的求法可知42105P ==． 考点：古典概率的求法．9. 设n A 为1(1)n x ++的展开式中含1n x -项的系数，n B 为1(1)n x -+的展开式中二项式系数的和，则能使n n A B ≥成立的n 的最大值是________．【答案】4【解析】【分析】由题意可得，A n ＝11n n C -+＝21n C +，12n n B -=，若使得A n ≥B n ，即n （n+1）≥2n ，可求n .【详解】∵（1+x ）n+1的展开式的通项为T r+11r r n C x +=，由题意可得，A n ＝11n n C -+＝21n C +，又∵n B 为1(1)n x -+的展开式中二项式系数的和，∴12n n B -=， ∵A n ≥B n ，∴2112n n C -+，即n （n+1）≥2n当n ＝1时，1×2≥2，满足题意；当n ＝2时，2×3≥22，满足题意；当n ＝3时，3×4≥23，满足题意；当n ＝4时，4×5≥24，满足题意；当n ＝5时，5×6＜25，不满足题意，且由于指数函数比二次函数增加的快，故当n≥5时，n （n+1）＜2n ，∴n ＝4. 故答案为4【点睛】本题主要考查了二项展开式的通项公式的应用，二项展开式的性质应用及不等式、指数函数与二次函数的增加速度的快慢的应用，属于中档题．10. 将4个不同的小球任意放入3个不同的盒子中，则每个盒子中至少有1个小球的概率为________． 【答案】49【解析】试题分析：将4个不同的小球任意放入3个不同的盒子中，每个小球有3种不同的放法，共有4381＝种放法，每个盒子中至少有1个小球的放法有12234236C C C =种，故所求的概率P =3681=49. 考点：1、排列组合；2、随机变量的概率.11. 若对于任意实数x ，都有1021001210(2)(2)(2)xa a x a x a x =+++++++，则3a 的值为_________.【答案】15360-【解析】【分析】 根据题意，分析可得1010[(2)2]x x =+-，求出其展开式，可得3a 为其展开式中含3(2)x +项的系数，由二项式定理求出3(2)x +项，分析可得答案．【详解】解：根据题意，1010[(2)2]x x =+-，其展开式的通项为10110(2)(2)r r r r T C x -+=+⨯-， 又由1021001210(2)(2)(2)x a a x a x a x =+++++⋯++，则3a 为其展开式中含3(2)x +项的系数，令7r =可得：7373810(2)(2)15360(2)T C x x =+⨯-=-+； 即315360a =-；故答案为：15360-．【点睛】本题考查二项式定理的应用，注意二项式定理的形式，属于基础题．12. 校园某处并排连续有6个停车位，现有3辆汽车需要停放，为了方便司机上下车，规定：当有汽车相邻停放时，车头必须同向；当车没有相邻时，车头朝向不限，则不同的停车方法共有__________种．（用数学作答）【答案】528【解析】(1)当三辆车都不相邻时有3348192A ⨯=(种)(2)当两辆车相邻时有33333333333424242434288A A A A A ⨯+⨯+⨯+⨯+⨯=(种)(3)当三辆车相邻时有334248A ⨯=(种)则共有19228848528++=(种)点睛：本题考查了排列组合问题，由于本题里是三辆车有六个位置，所以情况较多，需要逐一列举出来，注意当三辆车都不相邻时的情况要考虑周全，容易漏掉一些情况，然后利用排列组合进行计算即可．二、选择题（16分）：13. 某几何体的三视图如图所示，则该几何体的体积（单位：3cm ）是（ ）A. 43π+B. 23π+C. 43π+D. 423π+ 【答案】A【解析】由三视图可知，该几何体是半个圆柱和以圆柱轴截面为底面的四棱锥组成的组合体，其中半圆柱底面半径为1，高为2，体积为21122ππ⨯⨯⨯=，四棱锥体积为144133⨯⨯=，所以该几何体体积为43π+，故选A.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.14. 设A ，B ，C 是三个事件，给出下列四个事件： （Ⅰ）A ，B ，C 中至少有一个发生；（Ⅱ）A ，B ，C 中最多有一个发生；（Ⅲ）A ，B ，C 中至少有两个发生；（Ⅳ）A ，B ，C 最多有两个发生；其中相互为对立事件的是（ ）A. Ⅰ和ⅡB. Ⅱ和ⅢC. Ⅲ和ⅣD. Ⅳ和Ⅰ【答案】B【解析】【分析】利用互斥事件、对立事件的定义直接求解．【详解】解：A ，B ，C 是三个事件，给出下列四个事件：（Ⅰ）A ，B ，C 中至少有一个发生；（Ⅱ）A ，B ，C 中最多有一个发生；（Ⅲ）A ，B ，C 中至少有两个发生（Ⅳ）A ，B ，C 最多有两个发生；在A 中，Ⅰ和Ⅱ能同时发生，不是互斥事件，故A 中的两个事件不能相互为对立事件；在B 中，Ⅱ和Ⅲ既不能同时发生，也不能同时不发生，故B 中的两个事件相互为对立事件；在C 中，Ⅲ和Ⅳ能同时发生，不是互斥事件，故C 中的两个事件不能相互为对立事件；在D 中，Ⅳ和Ⅰ能同时发生，不是互斥事件，故D 中的两个事件不能相互为对立事件．故选：B ．【点睛】本题考查相互为对立事件的判断，考查互斥事件、对立事件的定义等基础知识，考查运算求解能力，属于基础题．15. 由曲线24x y =，24x y =-，4x =，4x =-围成图形绕y 轴旋转一周所得为旋转体的体积为1V ，满足2216x y +≤，22(2)4x y +-≥，22(2)4x y ++≥的点(,)x y 组成的图形绕y 轴旋一周所得旋转体的体积为2V ，则（ ） A. 1212V V = B. 1223V V = C. 12V V =D. 122V V =【答案】C【解析】【分析】由题意可得旋转体夹在两相距为8的平行平面之间，用任意一个与y 轴垂直的平面截这两个旋转体，设截面与原点距离为||y ，求出所得截面的面积相等，利用祖暅原理知，两个几何体体积相等．【详解】解：如图，两图形绕y 轴旋转所得的旋转体夹在两相距为8的平行平面之间， 用任意一个与y 轴垂直的平面截这两个旋转体，设截面与原点距离为||y ，所得截面面积21(44||)S y π=-， 22222(4)[4(2||)](44||)S y y y πππ=----=-12S S ∴=，由祖暅原理知，两个几何体体积相等，故选：C ．【点睛】本题主要考查祖暅原理的应用，求旋转体的体积的方法，体现了等价转化、数形结合的数学思想，属于基础题．16. a ，b 为空间两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以AC 为旋转轴选择，有下列结论：①当直线AB 与a 成60°角时，AB 与b 成30°角；②当直线AB 与a 成60°角时，AB 与b 成60°角；③直线AB 与a 所成角的最小值为45°；④直线AB 与a 所成角的最大值为60°；其中正确的是_______.（填写所以正确结论的编号）.A. ①③B. ①④C. ②③D. ②④ 【答案】C【解析】【分析】由题意知，a 、b 、AC 三条直线两两相互垂直，构建如图所示的边长为1的正方体，||1AC =，||2AB =斜边AB 以直线AC 为旋转轴，则A 点保持不变，B 点的运动轨迹是以C 为圆心，1为半径的圆，以C 坐标原点，以CD 为x 轴，CB 为y 轴，CA 为z 轴，建立空间直角坐标系，利用向量法能求出结果．【详解】解：由题意知，a 、b 、AC 三条直线两两相互垂直，画出图形如图，不妨设图中所示正方体边长为1，故||1AC =，||2AB =斜边AB 以直线AC 为旋转轴，则A 点保持不变，B 点的运动轨迹是以C 为圆心，1为半径的圆，以C 坐标原点，以CD 为x 轴，CB 为y 轴，CA 为z 轴，建立空间直角坐标系，则(1D ，0，0)，(0A ，0，1)，直线a 的方向单位向量(0a =，1，0)，||1a =，直线b 的方向单位向量(1b =，0，0)，1b ||=，设B 点在运动过程中的坐标中的坐标(cos B θ'，sin θ，0)，其中θ为B C '与CD 的夹角，[0θ∈，2)π，AB ∴'在运动过程中的向量，(cos AB θ'=，sin θ，1)-，||2AB '=， 设AB '与a 所成夹角为[0α∈，]2π， 则2cos |||sin |[012αθ==∈⨯，2]， [4πα∴∈，]2π，∴③正确，④错误．设AB '与b 所成夹角为[0β∈，]2π，2cos |||cos |12βθ==⨯， 当AB '与a 夹角为60︒时，即3πα=， 22|sin |cos 2cos 3πθα===， 22cos sin 1θθ+=，21cos |cos |22βθ∴==， [0β∈，]2π，3πβ∴=，此时AB '与b 的夹角为60︒，∴②正确，①错误．故选：C ．【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，属于中档题．三、解答题（48分）17. 已知矩形ABCD 内接于圆柱下底面的圆O ，PA 是圆柱的母线，若6AB =，8AD =，异面直线PB 与CD 所成的角为2arctan ，求此圆柱的体积.【答案】300π【解析】【分析】根据底面圆的内接矩形的长和宽求出圆的半径，再由母线垂直于底面和“异面直线PB 与CD 所成的角为2arctan ”求出母线长，代入圆柱的体积公式求出值．【详解】解：设圆柱下底面圆O 的半径为r ，连AC ，由矩形ABCD 内接于圆O ，可知AC 是圆O 的直径， ∴2226810r AC ==+=，得=5r ，由//AB CD ，可知PBA ∠就是异面直线PB 与CD 所成的角，即arctan2PBA ∠=，tan 2PBA ∴∠=．在直角三角形PAB 中，tan 12PA AB PBA =∠=，∴圆柱的体积22512300V r PA πππ==⨯⨯=．【点睛】本题考查了圆柱的体积求法，主要根据圆内接矩形的性质、母线垂直于底面圆求出它的底面圆半径和母线，即关键求出半径和母线长即可．18. 求二项式500(12)x +的展开式中项系数最大的项的系数.【答案】3333335002C ⋅或3343345002C ⋅【解析】【分析】根据题意，求出500(12)x +的展开式的通项，求出其系数，设第1r +项的系数最大，则有11500500115005002222r r r r r r r r C C C C --++⎧⎨⎩，解可得r 的值，代入通项中计算可得答案．【详解】解：根据题意，500(12)x +的展开式的通项为1500(2)r r r T C x +=，其系数为5002r r C ⨯，设第1r +项的系数最大，则有11500500115005002222r r r r r r r r C C C C --++⎧⎨⎩， 即11500499(5001)500499(5002)22!(1)!500499(5001)500499(500)22!(1)!r r r r r r r r r r r r -+⨯⨯⨯-+⨯⨯⨯-+⎧⎪-⎪⎨⨯⨯⨯-+⨯⨯⨯-⎪⎪+⎩解可得：333334r ，故当333r =或334r =时，展开式中项系数最大，则有4334334333355002T C x =，3333333333345002T C x =； 即系数最大的项的系数为3335003332C 或4335004332C ． 【点睛】本题考查二项式定理的应用，注意项的系数与二项式系数的区别，属于基础题．19. 如图，弧AEC 是半径为r 的半圆，AC 为直径，点E 为弧AC 的中点，点B 和点C 为线段AD 的三等分点，线段ED 与弧EC 交于点G ，平面AEC 外一点F 满足FC ⊥平面BED ，2FC r =.（1）求异面直线ED 与FC 所成角的大小；（2）将FCG ∆（及其内部）绕FC 所在直线旋转一周形成一几何体，求该几何体的体积.【答案】（1）90︒；（2）3415r π； 【解析】【分析】 （1）由FC ⊥平面BED ，利用线面垂直的性质定理可得FC ED ⊥，即可得到异面直线ED 与FC 所成角的大小为90︒．（2）连接GC ，在BGC ∆中，利用余弦定理得：2222222cos 5CG r r r CBG r =+-∠=，由题设知，所得几何体为圆锥，分别计算其其底面积及高为F ，即可得到该圆锥的体积V ．【详解】解：（1）FC ⊥平面BED ，ED ⊂平面BED ，FC ED ∴⊥，∴异面直线ED 与FC 所成角的大小为90︒．（2）连接GC ，在BGC ∆中，由余弦定理得：2222222cos 5CG r r r CBG r =+-∠=， 由题设知，所得几何体为圆锥，其底面积为2225CG r ππ=，高为2FC r =． 该圆锥的体积为2312423515V r r r ππ=⨯⨯=． 【点睛】熟练掌握线面垂直的性质定理、余弦定理、圆锥的体积计算公式是解题的关键．20. 老况、老王、老顾、小周、小郭和两位王女士共7人要排成一排拍散伙纪念照.（1）若两位王女士必须相邻，则共有多少种排队种数？（2）若老王与老况不能相邻，则共有多少种排队种数？（3）若两位王女士必须相邻，若老王与老况不能相邻，小郭与小周不能相邻，则共有多少种排队种数？【答案】（1）26261440A A =；（2）52563600A A =；（3）2222352116720C A A A A =； 【解析】【分析】（1）利用捆绑法即可求出，（2）利用插空法即可求出，（3）利用捆绑和插空法，即可求出．【详解】解：（1）首先把两位女士捆绑在一起看做一个符合元素，和另外5人全排列，故有26261440A A =种，（2）将老王与老况插入另外5人全排列所形成的6个空的两个，故有52563600A A =种，（3）先安排老王与老况，在形成的3个空中选2个插入小郭与小周，在形成的5个空中选1个插入老顾，最后将两位女士捆绑在一起看做一个符合元素，选1个位置插入到其余5人形成的6个空中故有2222352116720C A A A A =种． 【点睛】本题考查了简单的排列组合，考查了相邻问题和不相邻问题，属于中档题.21. 在一个圆锥内作一个内接等边圆柱（一个底面在圆锥的底面上，且轴截面是正方形的圆柱），再在等边圆柱的上底面截得的小圆锥内做一个内接等边圆柱，这样无限的做下去.（1）证明这些等边圆柱的体积从大到小排成一个等比数列；（2）已知这些等边圆柱的体积之和为原来圆锥体积的37，求最大的等边圆柱的体积与圆锥的体积之比. 【答案】（1）证明见解析；（2）38 【解析】【分析】（1）求出第一个等边圆柱的体积，设第n 个等边圆柱的底面半径为a ，其外接圆锥的底面半径为r ，高为h ，则其体积3322()2n rh V a r h ππ==+，进一步求得第1n +个等边圆柱的体积，作比可得这些等边圆柱的体积从大到小排成一个等比数列；（2）由这些等边圆柱的体积之和为原来圆锥体积的37可得r 与h 的关系，则答案可求． 【详解】（1）证明：如图，设圆锥的底面半径为r ，高为h ，内接等边圆柱的底面半径为a ，则由三角形相似可得：2a r a h r -=，可得2rh a r h=+． 其体积233222()2rh V a a a r h πππ===+． 设第n 个等边圆柱的底面半径为a ，其外接圆锥的底面半径为r ，高为h ， 则其体积3322()2n rh V a r hππ==+，再设第1n +个等边圆柱的底面半径为b ，则其外接圆锥的底面半径为2rh a r h =+， 高为22ah h r r h =+， 则第1n +个等边圆柱的体积223331222222()()2(2)22n rh h rh r h r h V b rh h r h r h r h ππ+++===++++． ∴31()2n n V h V r h +=+为定值， 则这些等边圆柱的体积从大到小排成一个以312()2rh V r h π=+为首项，以3()2h r h +为公比的等比数列； （2）解：原来圆锥的体积为213r h π， 这些等边圆柱的体积之和为32312232()214631()2rh V r h r h h q r rh h r h ππ+==-++-+． 由232223146373r h r h r rh h ππ=++，得222320r rh h +-=， 2h r ∴=．则最大的等边圆柱的体积为34r π，圆锥的体积为323r π，体积之比为38．【点睛】本题考查圆柱、圆锥体积的求法，考查等比数列的确定及所有项和公式的应用，是中档题．。

2015*2016学年度第二学期期末考试慕高二数学一、填空题1. 函数f (x) =cos( .X )( ■ • 0)的最小正周期为，则.=•6 52. 已知z=(2-i)2(i为虚数单位)，则复数z的虚部为•3.若sin ：• =2cos_：＞，贝y sin2二亠6cos2〉的值为.4. 某班有学生60人，现将所有学生按1, 2, 3, , , 60随机编号，若采用系统抽样的方法抽取一个容量为5的样本，已知编号为4, a, 28, b , 52的学生在抽取的样本中，则a • b =.5. 从1, 2, 3, 4, 5这5个数中，随机抽取2个不同的数，则这2个数的和为偶数的概率是.6. 某老师星期一到星期五收到信件数分别是10, 6, 8, 5, 6,该组数据的标准差为./ Z/1L *ci9.观察下列各式：55-3125 , 56=15625 , 57=78125，…，则52011的末四位数字为.10.在长为12cm的线段AB上任取一点C ,现作一矩形，邻边长分别等于线段AC , CB的长，则该矩形面积小于32cm2的概率为.7.已知函数隈三(0,二),cos.：:5’8.阅读如图所示的程序框图，运行相应的程序，若输入n的值为4,则输出S的值为.t| £ = $#2*七上|/Z/11. 已知函数f(x) =sin(• x；；'：：「:)(八0,-…：：：：：：：：…)图象上每一点的纵坐标不变，横坐标缩短为原来的一半后再向右平移 --个单位长度得到函数y二sin x的图象，贝U f (；) = •12. 若cos ) 3，则cos(5)-sin1 2)=.6 3 6 6113. 函数f(x)=3x3—3x，若方程f(x)=x2F在(U上两个解，则实数m的取值范围为•14. 若对任意的X・D，均有£(X)乞f(X)空f2(X)成立，则称函数f (x)为函数f1(x)到函数f2 (x)在区间f(x)上的“折中函数” •已知函数f (x) =(k -1)) x -1, g(x) =0,h(x) =(x T)ln x，且f (x)是g(x)到h(x)在区间[1,2e] 上的“折中函数”，则实数k的取值范围为.二、解答题15. 设复数z = -3cosv is in v . ( i为虚数单位)4(1 )当时，求| z |的值；3(2)当—[$,二]时，复数吕二COST - isi，且z,z为纯虚数，求二的值.16. 某校为调研学生的身高与运动量之间的关系，从高二男生中随机抽取100名学生的身高数据，得到如下频率分布表：1求频率分布表中①、②位置相应的数据；2为了对比研究学生运动量与身高的关系，学校计划采用分层抽样的方法从第2组和第5组中随机抽取7名学生进行跟踪调研，求第2组和第5组分别抽取的学生数？(3)在(2)的前提下，学校决定从7名学生中随机抽取2名学生接受调研访谈，求至少有1名学生来自第5组的概率？17. 已知函数f(x) = 2sin(x ) cosx.6IT(1 )若0 _ x _㊁，求函数f (x)的值域；(2)设：ABC的三个内角A,B,C所对的边分别为a,b,c，若A为锐角且f(A) =1,b =2,c =3，求cos(A-B)的值.18. 某公园准备建一个摩天轮，摩天轮的外围是一个周长为k米的圆，在这个圆上安装座位，且每个座位和圆心处的支点都有一根直的钢管相连，经预算，摩天轮上的每个座位与支点相连的钢管的费用为8k元/根，且当两相邻的座位之间的圆弧长为x米时，相邻两座位之间的钢管和其中一个座位的总费用为[(1024 x 20)x■ 2]k元，假设座位等距离分布，且至少100有两个座位，所有座位都视为点，且不考虑其他因素，记摩天轮的总造价为y元.(1)试写出y关于x的函数关系式，并写出定义域；(2)当k -100米时，试确定座位的个数，使得总造价最低？19. 已知函数f (x)二e x -mx k(m,k • R)定义域为(0, •：：).(1 )若k=2时，曲线y=f(x)在x=1和x=3处的切线互相平行，求实数m的值；(2 )若k =1时，函数f(x)在(1/：：)上有最小值，求实数m的取值范围；(3)若m =1时，函数f(x)在(1,=)上单调递增，求整数k的最大值.20. 已知函数f(x)=2x3 -3(k 1)x2 6kx t，其中k,t 为实数.(1)若函数f (x)在x=2处有极小值0,求k,t的值；(2)已知k _1且t =1-3k，如果存在(1,2]，使得「(冷)乞f(x。

2017-2018学年度高二第二学期期末考试数学试题（理科）一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集U 是实数集R ,集合}{22M x x x =<->或,{}2430N x x x =-+<,则图中阴影部分所表示的集合是 （） A ．}12|{<≤-x x B ．}22|{≤≤-x x C ．}21|{≤<x x D ．}2|{<x x2.下面是关于复数iiz ---=131的四个命题：其中的真命题为（）①在复平面内，复数z 对应的点位于第二象限②复数z 的虚部是-2 ③复数z 是纯虚数④5=zA. ①②B. ①③C. ②④D. ③④3．设0.213121log 3,,23⎛⎫=== ⎪⎝⎭a b c ,则（）A ．B ．C ．D ．4．已知向量a ＝(1，－cos θ)，b ＝(1，2cos θ)且a ⊥b ，则cos2θ等于( ) A ．－1 B ．0 C.12 D.225.在ABC ∆中，角A 、Ｂ、Ｃ所对的边分别是a 、b 、c，若a =，B A 2=，则B cos 等于（） A ．33 B ．43 Ｃ．53 Ｄ．63 6．将甲、乙、丙、丁四名学生分到三个不同的班，每个班至少分到一名学生，且甲、乙两名学生不能分到同一个班，则不同分法的种数为（）A.18B.24C.30D.367.若下框图所给的程序运行结果为=35S ，那么判断框中应填入的关于k 的条件是( )A.7k =B.6k ≤C.6k <D.6k >俯视图8.若某几何体的三视图(单位：cm )如图所示，则该几何体的 体积等于( )A.310cmB.320cmC.330cmD.340cm 9.下列说法中，正确的是（）A ．命题“若22am bm <，则a b <”的逆命题是真命题B ．命题“存在0,2>-∈x x R x ”的否定是：“任意0,2≤-∈x x R x ”C ．命题“p 或q ”为真命题，则命题“p ”和命题“q ”均为真命题D ．“0b =”是“函数2()f x ax bx c =++是偶函数”的充分不必要条件10．右图是函数y ＝A sin(ωx ＋φ)(00A ω>>，，||2πϕ≤)图像的一部分．为了得到这个函数的图像，只要将y ＝sin x (x ∈R)的图像上所有的点 ( )A .向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变.B .向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变.C .向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变. D .向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变.11.已知定义在R 上的函数()y f x =对任意x 都满足()()1f x f x +=-，且当01x ≤<时，()f x x =，则函数()()ln ||g x f x x =-的零点个数为( )A ．2B ．3 C.4 D ．512.定义在R 上的函数()f x 满足：()()1,(0)4,f x f x f '+>=则不等式()3x x e f x e >+（其中e 为自然对数的底数）的解集为（）A.()0,+∞B.()(),03,-∞+∞ C.()(),00,-∞+∞ D.()3,+∞二、填空题：本题共4小题，每小题5分，共20分.13.函数y f x =()的定义域为(]-∞，1，则函数y f x =-[log ()]222的定义域是________14.已知0(sin cos )a t t dt π=+⎰，则61()axx -的展开式中的常数项为. 15.函数)1,0(log 1)(≠>+=a a x x f a 的图像恒过定点A ，若点A 在直线02=-+ny mx 上，其中,0>mn 则nm 11+得最小值为. 16．已知函数()ln ,021,0x x f x x x >⎧=⎨+≤⎩若方程()f x ax =有三个不同的实数根，则a 的取值范围是．三、解答题：共70分.解答应写出文字说明、解答过程或演算步骤.第17~21题为必做题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.17.（本小题共12分）设数列10,10,}{11+==+n n n n a a S n a 项和为的前 9，9991+++n S a n n （1）求证：{}1+n a 是等比数列； (2)若数列{}n b 满足()()()*+∈+⋅+=N n a a b n n n 1lg 1lg 11,求数列{}n b 的前n 项和n T ；18.（本小题满分12分）如图，三棱柱111ABC A B C -中，侧棱1AA ⊥平面ABC ，ABC ∆为等腰直角三角形，90BAC ∠=，且1,,AB AA E F =分别是1,CC BC 的中点.（Ⅰ）求证：1B F ⊥平面AEF ；（Ⅱ）求锐二面角1B AE F --的余弦值.19.某高校在2017年的自主招生考试成绩中随机抽取n 名学生的笔试成绩（被抽取学生的成绩均不低于160分,且不高于185分），按成绩分组，得到的频率分布表如下左图所示. （1） 请先求出n 、a 、b 、c 的值，再在答题纸上补全频率分布直方图；（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？（3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A 考官进行面试， 第4组中有ξ名学生被考官A 面试，求ξ的分布列和数学期望.20.（本小题共12分）已知椭圆22221(0)x y a b a b+=>>的一个焦点F 与抛物线24y x =的焦点重合，且截，倾斜角为45的直线l 过点F . （Ⅰ）求该椭圆的方程；（Ⅱ）设椭圆的另一个焦点为1F ，问抛物线24y x =上是否存在一点M ，使得M 与1F 关于直线l 对称，若存在，求出点M 的坐标，若不存在，说明理由.FE C 1B 1A 1CBA21.（本小题共12分）已知函数()1x f x e x =--（Ⅰ）求()y f x =在点()1,(1)f 处的切线方程；（Ⅱ）若存在041,ln 3x ⎡⎤∈-⎢⎥⎣⎦，满足10xa e x -++<成立，求a 的取值范围；（Ⅲ）当0x ≥时，2()f x tx ≥恒成立，求t 的取值范围.选考题：请考生在第22、23题中任选一题作答.如果多做，按所做的第一题计分.作答时请写清题号． 22．(本小题满分10分)选修4—4：极坐标系与参数方程．在直角坐标系xoy 中，曲线C 1的参数方程为325425x t y t ⎧=-⎪⎪⎨⎪=-+⎪⎩(t 为参数)．曲线C 2: 2240x y y +-=，以坐标原点为极点，以x 轴正半轴为极轴建立极坐标系，若点P 的极坐标为(4π)．(I)求曲线C 2的极坐标方程； (Ⅱ)若C 1与C 2相交于M 、N 两点，求11PM PN+的值. 23．(本小题满分10分)选修4—5：不等式选讲 已知()()2f x x m m R =+∈．(I)当m =0时，求不等式()25f x x +-<的解集；(Ⅱ)对于任意实数x ，不等式()222x f x m --<成立，求m 的取值范围．2017-2018学年度高二第二学期期末考试数学试题（理科）答案一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.CCABB CDBBA BA二、填空题：本题共4小题，每小题5分，共20分. 13.2⎤⎡⋃--⎦⎣， 14. 25- 15. 2 16.1,（0）e三、解答题：共70分.解答应写出文字说明、解答过程或演算步骤.第17~21题为必做题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.17.（本小题共12分）解：（1）依题意，992=a ，故101112=++a a ， 当n S a n n n 9921+=≥-时， ①又9991++=+n S a n n ②②－①整理得：1011n 1n =+++a a ，故{}1+n a 是等比数列，（2）由（1）知，且()n n n qa a 101111=+=+-，()n a n =+∴1lg ，()11lg 1+=++n a n ()())1(11lg 1lg 11+=+⋅+=∴+n n a a b n n n()11431321211+++⨯+⨯+⨯=∴n n T n 11141313121211+-++-+-+-=n n ()*∈+=N n n n118.（本小题满分12分）（Ⅰ）连结AF ，∵F 是等腰直角三角形ABC ∆斜边BC 的中点，∴AF BC ⊥.又 三棱柱111ABC A B C -为直三棱柱， ∴面ABC ⊥面11BB C C ，∴AF ⊥面11BB C C ，1AF B F ⊥. 设11AB AA ==，则113222B F EF B E ===. ∴22211B F EF B E +=，∴1B F EF ⊥.FE C 1B 1A 1CBA又AFEF F =，∴1B F ⊥平面AEF .（Ⅱ）以F 为坐标原点，,FA FB 分别为,x y 轴建立直角坐标系如图，设11AB AA ==，则11(0,0,0),(,0,0),(0,(0,)2222F A B E -，1()2AE =-，1(AB =-.由（Ⅰ）知，1B F ⊥平面AEF ， ∴可取平面AEF的法向量1(0,m FB ==. 设平面1B AE 的法向量为(,,)n x y z =，10,0n AE nAB ⎧⎪⎧=⎪⎪⇒⎨⎨=⎪⎪⎩⎪⎩由∴可取(3,1,n =-.设锐二面角1B AE F --的大小为θ，则03(1)1cos |cos ,|||||m nmn m n θ⨯+-+⨯=<>===. ∴所求锐二面角1B AE F --的余弦值为619. （本小题共12分）【解】：（1）由第1组的数据可得100050.05==n ，第2组的频率b =350.0507.0=⨯，第2组的频数为a =35507.0100=⨯⨯人,第3组的频率为c =300.300100=,频率分布直方图如右:（2）因为第3、4、5组共有60名学生, 所以利用分层抽样在60名学生中抽取6名学生,每组分别为:第3组:306360⨯=人,… 6分第4组:206260⨯=人, …7分 第5组:106160⨯=人, …8分CC所以第3、4、5组分别抽取3人、2人、1人. （3）由题意知变量ξ的可能取值是0，1，2 该变量符合超几何分布，∴∴分布列是∴20. （本小题共12分）解：（Ⅰ）抛物线x y 42=的焦点为)0,1(F ，准线方程为1-=x ，∴122=-b a ①又椭圆截抛物线的准线1-=x，∴得上交点为)22,1(-，∴121122=+ba ② 由①代入②得01224=--b b ，解得12=b 或212-=b （舍去）， 从而2122=+=b a∴该椭圆的方程为该椭圆的方程为22121x y += （Ⅱ）∵倾斜角为45的直线l 过点F ，∴直线l 的方程为)1(45tan -=x y，即1-=x y ，由（Ⅰ）知椭圆的另一个焦点为)0,1(1-F ，设),(00y x M 与1F 关于直线l 对称，则得⎪⎪⎩⎪⎪⎨⎧--+=+-=⨯+-12)1(201110000x y x y ，解得⎩⎨⎧-==2100y x ，即)2,1(-M ， 又)2,1(-M 满足x y 42=，故点M 在抛物线上.所以抛物线x y 42=上存在一点)2,1(-M ，使得M 与1F 关于直线l 对称. 21. （本小题共12分）解：(Ⅰ) ()1xf x e '=-()12f e =-()f x ∴在()()1,1f 处的切线方程为： ()()211y e e x -+=--即()11y e x =--(Ⅱ) 1x a e x <-- 即()a f x < 令()10xf x e '=-=0x =0x >时，()0f x '>，0x <时，()0f x '< ()f x ∴在(),0-∞上减，在()0,+∞上增又041,ln 3x ⎡⎤∈-⎢⎥⎣⎦时，()f x ∴的最大值在区间端点处取到.()11111f e e --=-+=444ln 1ln333f ⎛⎫=-- ⎪⎝⎭()41441141ln 1ln ln 033333f f e e ⎛⎫--=-++=-+> ⎪⎝⎭()41ln 3f f ⎛⎫∴-> ⎪⎝⎭()f x ∴在41,ln 3⎡⎤-⎢⎥⎣⎦上最大值为1e ，故a 的取值范围是：a <1e .（Ⅲ）由已知得0,x ≥时210xe x tx ---≥恒成立，设()21.xg x e x tx =---()'12.xg x e tx ∴=--由(Ⅱ)知1xe x ≥+，当且仅当0x =时等号成立， 故()()'212,g x x tx t x ≥-=-从而当120,t -≥即12t ≤时，()()'00g x x ≥≥，()g x ∴为增函数，又()00,g = 于是当0x ≥时，()0,g x ≥即2(),f x tx ≥12t ∴≤时符合题意。

2017学年第二学期七宝中学高二期末考试数学试题一、填空题1.将三份录取通知书投入四个邮筒共有_______种不同的投递方式。

2.若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的底面半径为____。

3.已知空间向量，如(21,3,0),(1,,3)(,)a x x b y y x y R =+=-∈果存在实数λ使得a b λ=成立，则x y +=_______.4.在6(2)x x+展开式中，常数项为_______。

（用数字作答） 5.从一堆苹果中任取6个，称得它们的质量如下（单位：克）：125，124，121，123，127，则该样本标准差s =______克。

6，在上海高考改革方案中，要求每位高中生必须在物理、化学、生物、政治、历史、地理6门学科（3门理科，3门文科）中选择3门参加等级考试，小李同学受理想中的大学专业所限，决定至少选择一门理科学科，那么小李同学的选科方案有____种。

7.若在1()n x x-展开式中，若奇数项的系数之和为32，则含4x 的系数是______。

8，已知实数,x y 满足不等式组340210380x y x y x y -+≥+-≥+-≤，若目标函数z x ay =+恰好仅在点(2,2)处取得最大值，则实数a 的取值范围为_______.9.在9()a b c ++的展开式中，含432a b c 项的系数为______（用数字作答）10．已知,x y 满足组合数方程21717x yC C =，则xy 的最大值是_______.11.设集合{1,2,3,4,5}I =，选择I 的两个非空子集A 和B ，要使B 中最小的数大于A 中最大的数，则不同的选择方法共有______种。

12．如图，AD 与BC 是四面体ABCD 中互相垂直的棱，2,2,,EC c AB BC AC CD a a c =+=+=且其中,为常数，则四面体ABCD 的体积最大值是_______.二、选择题13．一个空间几何体的三视图如图所示，则该几何体的体积为（ ） A．2π+11111左视图主视图B．4π+ C．2π+D．43π+14．从2018名学生志愿者中选取50名学生参加活动，若采用下面的方法选取，先用简单随机抽样从2018人中剔除18人，剩下的2000人再按系统抽样的方法抽取50人，则在2018人中，每人入选的概率（ ）A ．不全相等 B.均不相等 C ．都相等，且为140 D.都相等，且为25100915．为了研究某药厂的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：kPa ）的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组、第二组、……，第五组，右图是根据实验数据制成的频率分布直方图，已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为（ ）A ．6 B. 8 C.12 D.1816.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，期中记载有求“盖”的术：置如其周，令相承也；又以高乘之。

2017-2018学年上海市闵行区七宝中学高二（下）期末数学试卷(J)副标题题号一二三总分得分一、选择题（本大题共4小题，共4.0分）1.一个空间几何体的三视图如图所示，则该几何体的体积为()A. 2π+2√3B. 4π+2√3C. 2π+2√33D. 4π+2√33【答案】C【解析】解：由三视图得，该空间几何体为一圆柱和一四棱锥组成的，并且圆柱的底面半径为1，高为2，体积为2π，四棱锥的底面边长为√2，高为√3，体积为1 3×√2×√2×√3=2√33，所以该几何体的体积为2π+2√33．故选：C．由三视图判断空间几何体是由下圆柱和上四棱锥组成，并根据三视图求出圆柱的半径和高，四棱锥的边长和高，代入对应的体积公式分别求解，最后再和在一起．本题的考点是由三视图求几何体的体积，需要由三视图判断空间几何体的结构特征，并根据三视图求出每个几何体中几何元素的长度，代入对应的体积公式分别求解，考查了空间想象能力．2.从2018名学生志愿者中选取50名学生参加活动，若采用下面的方法选取，先用简单随机抽样从2018人中剔除18人，剩下的2000人再按系统抽样的方法抽取50人，则在2018人中，每人入选的概率()A. 不全相等B. 均不相等C. 都相等，且为140D. 都相等，且为251009【答案】D【解析】解：∵在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，在剔除过程中，每个个体被剔除的概率相等，∴每个个体被抽到包括两个过程，一是不被剔除，二是选中，这两个过程是相互独立的，∴每人入选的概率p=502018=251009，故选：D．根据简单随机抽样与系统抽样方法的定义，结合概率的意义，即可判断每个人入选的概率是多少．本题考查了简单随机抽样与系统抽样方法的应用问题，也考查了概率的意义问题，是基础题目．3.为了研究某药品的疗效，选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位：kPa)的分组区间为[12,13)，[13,14)，[14,15)，[15,16)，[16,17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为()A. 6B. 8C. 12D. 18【答案】C【解析】解：由直方图可得分布在区间第一组与第二组共有20人，分布在区间第一组与第二组的频率分别为0.24，0.16，所以第一组有12人，第二组8人，第三组的频率为0.36，所以第三组的人数：18人，第三组中没有疗效的有6人，第三组中有疗效的有12人．故选：C．由频率=频数样本容量以及直方图可得分布在区间第一组与第二组共有20人的频率，即可求出第三组中有疗效的人数得到答案；本题考查古典概型的求解和频率分布的结合，列举对事件是解决问题的关键，属中档题．4.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈136L2ℎ，它实际上是将圆锥体积公式中的圆周率π近似取为3，那么，近似公式V≈275L2ℎ相当于将圆锥体积公式中的π近似取为()A. 227B. 258C. 15750D. 355113【答案】B【解析】解：设圆锥底面圆的半径为r，高为h，则L=2πr，∴13πr2ℎ=275(2πr)2ℎ，∴π=258．故选：B．根据近似公式V≈275L2ℎ，建立方程，即可求得结论．本题考查圆锥体积公式，考查学生的阅读理解能力，属于基础题．二、填空题（本大题共12小题，共12.0分）5.将三份录取通知书投入四个邮筒共有______种不同的投递方式．【答案】64【解析】解：根据题意，将三份录取通知书投入四个邮筒，每份通知书有4种投放方法，则3份通知书有4×4×4=64种投放方法；故答案为：64．根据题意，分析可得三份录取通知书中，每份通知书有4种投放方法，由分步计数原理计算可得答案．本题考查分步计数原理的应用，注意题目的限制条件，属于基础题．6.若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的底面半径为______．【答案】1【解析】解：设圆锥的母线长为R，底面半径为r，则：πR=2πr，∴R=2r，∵一个圆锥的侧面展开图是面积为2π的半圆面，∴S=πRr=2πr2=2π，解得r=1．故答案为：1．设出圆锥的半径与母线长，利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长，进而能求出结果．本题考查圆锥的底面半径的求法，考查圆锥的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．7.已知空间向量，如a⃗=(2x+1,3x，0)，b⃗ =(1,y，y−3)(x，y∈R)果存在实数λ使得a⃗=λb⃗ 成立，则x+y=______．【答案】2【解析】解：∵a⃗=(2x+1,3x，0)，b⃗ =(1,y，y−3)(x，y∈R)存在实数λ使得a⃗=λb⃗ 成立，∴{2x+1=λ3x=λy0=λ(y−3)，解得y=3，x=λ=−1，则x+y=3−1=2．故答案为：2．由a⃗=(2x+1,3x，0)，b⃗ =(1,y，y−3)(x，y∈R)存在实数λ使得a⃗=λb⃗ 成立，可得{2x+1=λ3x=λy0=λ(y−3)，解出即可得出．本题考查了向量共线定理、向量相等、方程组的解法，考查了推理能力与计算能力，属于基础题．8.二项式(2x√x)6的展开式的常数项为______．【答案】60【解析】解：设二项式(2x+√x)6的展开式的通项为T r+1，则Tr+1=C6r⋅(2x)6−r⋅x−12r=C6r⋅26−r⋅x6−32r，令6−32r=0得：r=4，∴二项式(2x√x)6的展开式的常数项为T5=C64⋅22=15×4=60．故答案为：60．利用二项展开式的通项Tr+1=C6r⋅26−r⋅x6−32r中x的幂指数为0求得r，从而可求二项式(2x√x)6的展开式的常数项．本题考查二项式定理的应用，突出考查二项展开式的通项公式，属于中档题．9.从一堆苹果中任取5只，称得它们的质量如下(单位：克)125 124 121 123 127则该样本标准差s=______(克)(用数字作答)．【答案】2【解析】解：∵x=15(125+124+121+123+127)=124，∴S2=15[(125−124)2+(124−124)2+(121−124)2+(123−124)2+(127−124)2]=4，∴S=√4=2．故答案为：2．先求出这五个数的平均数，再求出方差，由此能求出这五个数的标准差．本题考查一组数据的标准差的求法，是基础题，解题时要注意方差公式的灵活运用．10.在上海高考改革方案中，要求每位高中生必须在物理、化学、生物、政治、历史、地理6门学科(3门理科，3门文科)中选择3门参加等级考试，小李同学受理想中的大学专业所限，决定至少选择一门理科学科，那么小李同学的选科方案有______种. 【答案】19【解析】解：根据题意，从物理、化学、生物、政治、历史、地理6门学科任选3门，有C 63=20种选取方法，其中全部为文科科目、即没有理科科目的选法有1种， 则至少选择一门理科学科的选法有20−1=19种； 故答案为：19．根据题意，用间接法分析：首先计算从6门学科任选3门的选法，再分析其中全部为文科科目、即没有理科科目的选法，分析可得答案．本题考查排列、组合的应用，注意利用间接法分析，避免分类讨论．11. 若在(x −1x )n 展开式中，若奇数项的系数之和为32，则含x 4的系数是______． 【答案】−6【解析】解：在(x −1x )n 展开式中，若奇数项的系数之和为2n−1=32，求得n =6，则通项公式为T r+1=C 6r⋅(−1)r ⋅x 6−2r ，令6−2r =4，求得r =1，故含x 4的系数是C 61⋅(−1)=−6， 故答案为：−6．由题意利用二项式系数的性质，求出再利用二项式的通项公式，求出含x 4的系数． 本题主要考查二项式系数的性质，二项展开式的通项公式的应用，属于基础题．12. 已知实数x ，y 满足不等式组{x −3y +4≥0x +2y −1≥03x +y −8≤0，若目标函数z =x +ay 恰好仅在点(2,2)处取得最大值，则实数a 的取值范围为______． 【答案】(13,+∞)【解析】解：画出已知约束条件的可行域为△ABC 内部(包括边界)如图，易知当a =0时，不符合题意；当a >0时，由目标函数z =x +ay 得y =−1a x +za ， 则由题意得−3=k AC <−1a <0，故a >13． 综上所述，a >13． 故答案为：(13,+∞)．画出可行域，利用几何意义求最值的方法，利用直线斜率之间的关系，只需求出直线z =x +ay 的斜率的取值范围即可．本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题.由于线性规划的介入，借助于平面区域，可以研究函数的最值或最优解；借助于平面区域特性，我们还可以优化数学解题，借助于规划思想，巧妙应用平面区域，为我们的数学解题增添了活力．13. 在(a +b +c)9的展开式中，含a 4b 3c 2项的系数为______(用数字作答)【答案】1260【解析】解：(a+b+c)9表示9个因式(a+b+c)的乘积，故其中有4个因式取a，3个因式取b，剩下的2个因式取c，可得含a4b3c2项，故含a4b3c2项的系数为C94⋅C53⋅C22=1260，故答案为：1260．根据乘方意义，应用排列组合的知识，求出含a4b3c2项的系数．本题主要考查乘方意义，排列组合的知识，属于基础题．14.已知x，y满足组合数方程C172x=C17y，则xy的最大值是______．【答案】128【解析】解：∵x，y满足组合数方程C172x=C17y，∴2x=y，0≤x≤8或2x+y=17，∴xy=2x2∈[0,128]，或2xy≤(2x+y2)2=2894，即xy≤2898．综上，当2x=y=16时，xy取最大值128．故答案为：128．由组合数公式的性质得2x=y，0≤x≤8或2x+y=17，从而xy=2x2∈[0,128]，或2xy≤(2x+y2)2=2894，由此得到当2x=y=16时，xy取最大值128．本题考查两数积的最大值的求法，考查组合数公式的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．15.集合I={1,2，3，4，5}.选择I的两个非空子集A和B，要使B中的最小数大于A中的最大数，则不同的选择方法有______种.【答案】49【解析】解：集合A、B中没有相同的元素，且都不是空集，从5个元素中选出2个元素，有C52=10种选法，小的给A集合，大的给B集合；从5个元素中选出3个元素，有C53=10种选法，再分成1一个元素一组、2个元素一组，有两种分法，较小元素的一组给A集合，较大元素的一组的给B集合，共有2×10=20种方法；从5个元素中选出4个元素，有C54=5种选法，再分成1个元素一组、3三个元素一组；2个元素一组、2个元素一组；3个元素一组、1一个元素一组，共三种分法，较小元素的一组给A集合，较大元素的一组的给B集合，共有3×5=15种方法；从5个元素中选出5个元素，有C55=1种选法，再分成1个元素一组、4个元素一组；2个元素一组、3个元素一组；3个元素一组、2个元素一组；4个元素一组、1两个元素一组组，有四种分法，较小元素的一组给A集合，较大元素的一组的给B集合，共有4×1=4种方法；总计为10+20+15+4=49种方法．故答案为：49根据题意，B中最小的数大于A中最大的数，则集合A、B中没有相同的元素，且都不是空集，按A、B中元素数目这和的情况，分4种情况讨论，分别计算其选法种数，进而相加可得答案．本题考查排列组合的实际应用，本题解题的关键是理解题意，能够看懂使B中的最小数大于A中的最大数的意义，本题是一个难题也是一个易错题，需要认真解答．16.如图，AD与BC是四面体ABCD中互相垂直的棱，BC=2，若AD=2c，且AB+BD=AC+CD=2a，其中a、c为常数，则四面体ABCD的体积的最大值是______．【答案】23c√a2−c2−1【解析】解：作BE⊥AD于E，连接CE，则AD⊥平面BEC，所以CE⊥AD，由题设，B与C都是在以AD为焦点的椭球上，且BE、CE都垂直于焦距AD，AB+BD=AC+CD=2a，显然△ABD≌△ACD，所以BE=CE．取BC中点F，∴EF⊥BC，EF⊥AD，要求四面体ABCD的体积的最大值，因为AD是定值，只需三角形EBC的面积最大，因为BC是定值，所以只需EF最大即可，当△ABD是等腰直角三角形时几何体的体积最大，∵AB+BD=AC+CD=2a，∴AB=a，所以EB=√a2−c2，EF=√a2−c2−1，所以几何体的体积为：13×2×√a2−c2−1×2c×12=23c√a2−c2−1．故答案为：23c√a2−c2−1．作BE⊥AD于E，连接CE，说明B与C都是在以AD为焦距的椭球上，且BE、CE都垂直于焦距AD，BE=CE．取BC中点F，推出四面体ABCD的体积的最大值，当△ABD是等腰直角三角形时几何体的体积最大，求解即可．本题考查棱柱、棱锥、棱台的体积，考查空间想象能力，逻辑推理能力以及计算能力．三、解答题（本大题共5小题，共5.0分）17.毕业季有6位好友欲合影留念，现排成一排，如果：(1)A、B两人不排在一起，有几种排法？(2)A、B两人必须排在一起，有几种排法？(3)A不在排头，B不在排尾，有几种排法？【答案】解：(1)将A、B两人插入到其余4人所形成的5个空中，故有A44A52=480种，(2)将A、B两人捆绑在一起看做一个复合元素和其余4人去安排了，故有A22A55=240种，(3)根据题意，分2种情况讨论：①若A在排尾，则剩下的5人全排列，故有A55=120种排法，②若A不在排尾，在A有4个位置可选，B有4个位置可选，将剩下的4人全排列，安排在其他4个位置即可，此时有C41C41A44=388种排法，则一共有120+388=508种不同的排法；【解析】(1)利用插空法即可求出；(2)利用捆绑法即可求出，；(3)根据题意，分2种情况讨论：①若A在排尾，②若A不在排尾，分别求出每一种情况的排法数目，由加法原理计算可得答案．本题考查排列、组合的应用，注意优先分析受到限制的元素．18. 已知在二项式(√x 32√x 3)n 的展开式中，前三项系数的绝对值成等差数列．(1)求正整数n 的值；(2)求展开式中二项式系数最大的项； (3)求展开式中系数最大的项；【答案】解：(1)二项式(√x 3+2√x 3)n 的展开式中，前三项系数的绝对值成等差数列，可得2C n1⋅12=C n 0+C n 2⋅14，解得n =1(舍去)，或n =8； (2)第r +1项的二项式系数为T r+1=C 8r，故第5项的二项式系数最大，此时，r =4； (3)由{C 8r(12)r ≥C 8r+1(12)r+1C 8r (12)r ≥C 8r−1(12)r−1，解得2≤r ≤3．∴系数最大的项为第三项．【解析】(1)由等差数列的性质列式求得n =8；(2)根据二项式系数的性质，求得二项式系数最大的项；(3)由{C 8r(12)r ≥C 8r+1(12)r+1C 8r (12)r ≥C 8r−1(12)r−1，解得2≤r ≤3，结合通项公式可得第三项的系数最大． 本题主要考查二项式定理的应用，二项式系数、二项式的系数的定义和性质，属于中档题．19. 已知直线C 1{y =tsinαx=1+tcosα(t 为参数)，C 2{y =sinθx=cosθ(θ为参数)，(Ⅰ)当α=π3时，求C 1与C 2的交点坐标；(Ⅱ)过坐标原点O 做C 1的垂线，垂足为A ，P 为OA 中点，当α变化时，求P 点的轨迹的参数方程，并指出它是什么曲线．【答案】解：(Ⅰ)当α=π3时，C 1的普通方程为y =√3(x −1)，C 2的普通方程为x 2+y 2=1． 联立方程组{y =√3(x −1)x 2+y 2=1，解得C 1与C 2的交点为(1,0)(12,−√32)．(Ⅱ)C 1的普通方程为xsinα−ycosα−sinα=0①．则OA 的方程为xcosα+ysinα=0②，联立①②可得x =sin 2α，y =−cosαsinα； A 点坐标为(sin 2α,−cosαsinα)，故当α变化时，P 点轨迹的参数方程为：{x =12sin 2αy =−12sinαcosα(α为参数)， P 点轨迹的普通方程(x −14)2+y 2=116． 故P 点轨迹是圆心为(14,0)，半径为14的圆．【解析】(I)先消去参数将曲线C1与C2的参数方程化成普通方程，再联立方程组求出交点坐标即可，(II)设P(x,y)，利用中点坐标公式得P点轨迹的参数方程，消去参数即得普通方程，由普通方程即可看出其是什么类型的曲线．本题主要考查直线与圆的参数方程，参数方程与普通方程的互化，利用参数方程研究轨迹问题的能力．20.将4个不同的红球和6个不同的白球放入同一个袋中，现从中取出4个球．(1)若取出的红球的个数不少于白球的个数，则有多少种不同的取法；(2)取出一个红球记2分，取出一个白球记1分，若取出4个球的总分不少于5分，则有多少种不同的取法；(3)若将取出的4个球放入一箱子中，记“从箱子中任意取出2个球，然后放回箱子中”为一次操作，如果操作三次，求恰有一次取到2个红球且有一次取到2个白球的概率．【答案】解：(1)若取出的红球的个数不少于白球的个数，则有4红和3红1白两类，其中：4红有：C44C60=1种不同的取法；3红1白有：C43C61=24种不同的取法；故共有25种不同的取法；(2)若取出4个球的总分不少于5分，则有4红和3红1白，2红2白，1红3白四类，其中：4红有：C44C60=1种不同的取法；3红1白有：C43C61=24种不同的取法；2红2白有：C42C62=90种不同的取法；1红3有：C41C63=80种不同的取法；故共有195种不同的取法；(3)若将取出的4个球放入一箱子中，记“从箱子中任意取出2个球，然后放回箱子中”为一次操作，如果操作三次，共有：(C42⋅C21)⋅(C32⋅C21)⋅(C22⋅C21)=144种不同情况；恰有一次取到2个红球且有一次取到2个白球共有：1+2+1+2=6种情况，故恰有一次取到2个红球且有一次取到2个白球的概率P=6144=124【解析】(1)若取出的红球的个数不少于白球的个数，则有4红和3红1白两类，进而可得答案；(2)若取出4个球的总分不少于5分，则有4红和3红1白，2红2白，1红3白四类，进而可得答案；(3)求出操作三次的情况总数，及恰有一次取到2个红球且有一次取到2个白球的情况数，可得答案．本题考查概率的求法，考查列举法、古典概型等基础知识，考查运算求解能力，考查函数与方程思想，第三问难度均大21.在四棱锥P−ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2，以AC的中心O为球心、AC为直径的球面交PD于点M，交PC于点N．(1)求证：AM⊥平面PCD；(2)求直线CD与平面ACM所成角的大小；(3)求点N到平面ACM的距离．【答案】(1)证明：依题设知，AC是所作球面的直径，则AM⊥MC．∵P A⊥平面ABCD，则PA⊥CD，又CD⊥AD，∴CD⊥平面PAD，则CD⊥AM，∴A M⊥平面PCD；(2)解：由(1)知，AM⊥PD，又PA=AD，则M是PD的中点可得AM=2√2，MC=√MD2+CD2=2√3，则S△ACM=12AM⋅MC=2√6．设D到平面ACM的距离为h，由V D−ACM=V M−ACD，得2√6ℎ=8，可求得ℎ=2√63，设直线CD与平面ACM所成角的大小为θ，则sinθ=ℎCD =√63，∴θ=arcsin√63；(3)解：由已知求得PC=6．∵AN⊥NC，由PNPA =PAPC，得PN=PA2PC=83．∴NCPC =59．故N点到平面ACM的距离等于P点到平面ACM距离的59．又∵M是PD的中点，则P、D到平面ACM的距离相等，由(2)可知所求距离为59ℎ=10√627．【解析】(1)依题设知，AC是所作球面的直径，则AM⊥MC.由P A⊥平面ABCD，得PA⊥CD，结合CD⊥AD，可得CD⊥平面PAD，则CD⊥AM，再由线面垂直的判定可得A M⊥平面PCD；(2)先根据体积相等求出D到平面ACM的距离为h，即可求直线PC与平面ABM所成的角；(3)先根据条件分析出所求距离等于点P到平面ACM距离的59，设点P到平面ACM距离为h，再利用第二问的结论即可得到答案．本题考查直线与平面所成的角，平面与平面垂直的判定，考查空间想象能力，逻辑思维能力，计算能力，是中档题．。

高二下学期期末考试数学试题（考试时间：120分钟 满分：150分 ）一、填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1.过点)2,1(、)6,3(的直线的斜率为______________．2.若i 是虚数单位，复数z 满足5)43(=-z i ,则z 的虚部为_________．3.正四面体ABC S -的所有棱长都为2，则它的体积为________．4.以)2,1(-为圆心且过原点的圆的方程为_____________．5.从一副52张扑克牌中第一张抽到“Q ”，重新放回，第二张抽到一张有人头的牌，则这两个事件都发生的概率为________．6.已知圆锥的高与底面半径相等，则它的侧面积与底面积的比为________．7.正方体1111D C B A ABCD -中，二面角111C D A B --的大小为__________．8.双曲线1422=-y x 的顶点到其渐近线的距离等于_________． 9.某人5次上班途中所花的时间（单位：分钟）分别为9,11,10,,y x .已知这组数据的平均数为10，方差为2，则=-||y x __________．10.在长方体1111D C B A ABCD -中，已知36,91==BC AA ，N 为BC 的中点，则直线11C D 与平面N B A 11的距离是___________．11.棱长为1的正方体1111D C B A ABCD -的8个顶点都在球面O 的表面上，E 、F 分别是棱1AA 、1DD 的中点，则直线EF 被球O 截得的线段长为________．12.从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外 科和内科医生都至少有1人的选派方法种数是___________．(用数字作答)13.在棱长为1的正方体盒子里有一只苍蝇，苍蝇为了缓解它的无聊，决定要考察这个盒子的每一个角，它从一个角出发并回到原处，并且每个角恰好经过一次，为了从一个角到另一个角，它或直线飞行，或者直线爬行，苍蝇的路径最长是____________．（苍蝇的体积不计）14.设焦点是)5,0(1-F 、)5,0(2F 的双曲线C 在第一象限内的部分记为曲线T ，若点ΛΛ),,(),,2(),,1(2211n n y n P y P y P 都在曲线T 上，记点),(n n y n P到直线02:=+-k y x l 的距离为),2,1(Λ=n d n ,又已知5lim =∞→n n d ，则常数=k ___________． 二、选择题（本大题共有4题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.15.一个圆柱形的罐子半径是4米，高是9米，将其平放，并在其中注入深2米的水，截面如图所示，水的体积是（ ）平方米.A ．32424-πB ．33636-πC ．32436-πD ．33648-π第15题图16.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70), [70,80),[80,90), [90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为（ ）A ．588B ．480C ．450D ．12017.使得*)()13(N n x x x n ∈+的展开式中含有常数项的最小的n 为 （ ） A ．4B ．5C ．6D ．7 18.若直线m x y l +-=2:与曲线|4|21:2x y C -=有且仅有三个交点，则m 的取值范围是（） A ．)12,12(+- B ．)2,1( C ．)12,1(+ D ．)12,2(+三、解答题（本大题共有5题，满分74分）解答下列各题必须在答题纸相应编号的规定区域写出必要的步骤．19.（12分）求8)32(xx +的二项展开式中的第5项的二项式系数和系数.20.（14分）某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者从装有3个红球、1 个蓝球、6奖如下:奖级 摸出红、蓝球个数 获奖金额一等奖 3红1蓝 200元二等奖 3红1白 50元三等奖 2红1蓝或2红2白 10元(1)求一次摸奖恰好摸到1个红球的概率；(2)求摸奖者在一次摸奖中获奖金额X 的分布列与期望()E X .21.（14分）已知椭圆13422=+y x 上存在两点A 、B 关于直线m x y +=4对称，求m 的取值范围.22.（16分）如图，四棱柱1111D C B A ABCD -中, 侧棱⊥A A 1底面ABCD ，AD AB DC AB ⊥,//， 1==CD AD ，21==AB AA ，E 为棱1AA 的中点.(1) 证明：CE C B ⊥11；(2) 设点M 在线段E C 1上, 且直线AM 与平面11A ADD 所成角的正弦值为62, 求线段AM 的长.23.（18分）下图是利用计算机作图软件在直角坐标平面xOy 上绘制的一列抛物线和一列直线，在焦点为n F 的抛物线列x p y C n n 4:2=中，n p 是首项和公比都为)10(<<p p 的等比数列，过n F 作斜率2的直线n l 与n C 相交于n A 和n B （n A 在x 轴的上方，n B 在x 轴的下方）.（1）证明：n OA 的斜率是定值；（2）求1A 、2A 、Λ、n A 、Λ所在直线的方程；（3）记n n OB A ∆的面积为n S ，证明：数列}{n S 是等比数列，并求所有这些三角形的面积的和.第22题图 E D 1 C 1 B 1 A 1 D C B A金山中学第二学期高二年级数学学科期末考试卷参考答案19.（12分）解：4485)32)((xx C T =， 所以二项式系数为7048=C ，系数为811120. 20.（14分）解：（1）214103713=C C C ； X0 10 50 200 P(X) 4231 358 351 2101 321020035503510420)(=⋅+⋅+⋅+⋅=X E . 21.（14分）解：设直线AB 方程为b x y +-=4，联立 ⎪⎩⎪⎨⎧+-==+,4,124322b x y y x 得,0481681322=-+-b bx x 从而,138b x x B A =+ ,13242)(41b b x x y y B A B A =++-=+ 则B A ,中点是)1312,134(b b ，则,013121344=+-⋅m b b 解得.134b m -= 由0481681322=-+-b bx x 有实数解得,0)4816(526422≥--=∆b b 即.4132≤b 于是.413)413(2≤-m 则m 的取值范围是.1313213132≤≤-m23.（18分）解：（1）由已知得n n p p =，抛物线焦点)0,(n n p F ，抛物线方程为x p y n 42=，直线n l 的方程为).(2np x y -=于是，抛物线n C 与直线n l 在x 轴上方的交点),(11y x A n 的坐标满足⎪⎩⎪⎨⎧-==),(2,411121n n p x y x p y 则有,042211121=-+x y x y而直线n OA 的斜率为11x y k n OA =，则,042112=-+OA OA k k 解得,51±-=n OA k 又,0>k 点n A 在第一象限，则51+-=n OA k ；（2）直线方程为x y )51(+-=；（3）由⎪⎩⎪⎨⎧-==),(2,42n n p x y x p y 得,04222=--n n p y p y 则n p AB 10||=， 而O 到直线n l 的距离为52np ，于是n n OB A ∆的面积n n p S 252=，所以数列}{n S 是以252p 为首项，2p 为公比的等比数列.由于10<<p ， 所以所有三角形面积和为22152pp -.高二下学期期末考试数学试题（考试时间：120分钟 满分：150分 ）一、填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1.过点)2,1(、)6,3(的直线的斜率为______________．2.若i 是虚数单位，复数z 满足5)43(=-z i ,则z 的虚部为_________．3.正四面体ABC S -的所有棱长都为2，则它的体积为________．4.以)2,1(-为圆心且过原点的圆的方程为_____________．5.某几何体的三视图如图所示,则该几何体的体积为__________．6.已知圆锥的高与底面半径相等，则它的侧面积与底面积的比为________．7.正方体1111D C B A ABCD -中，二面角111C D A B --的大小为__________． 8.双曲线1422=-y x 的顶点到其渐近线的距离等于_________． 9.已知球的半径为1，A 、B 是球面上两点，线段AB 的长度为3，则A 、B 两点的球面距离为 ________．10.在长方体1111D C B A ABCD -中，已知36,91==BC AA ，N 为BC 的中点，则直线11C D 与 平面N B A 11的距离是___________．11.从3名骨科、4名脑外科和5名内科医生中选派6人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是___________(用数字作答)．12. 已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ,过点F 的直线交椭圆于,A B 两点.若 AB 的中点坐标为(1,1)-,则E 的方程为_________________．13.设实数y x ,满足⎪⎩⎪⎨⎧≤-≥-+≤--,032,042,02y y x y x 则y x z -=2的最大值为____________.14.在棱长为1的正方体盒子里有一只苍蝇，苍蝇为了缓解它的无聊，决定要考察这个盒子的每一 个角，它从一个角出发并回到原处，并且每个角恰好经过一次，为了从一个角到另一个角，它或直 线飞行，或者直线爬行，苍蝇的路径最长是____________．（苍蝇的体积不计）二、选择题（本大题共有4题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编 号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.15.在正方体1111D C B A ABCD -中，任取两条棱，则这两条棱为异面直线的概率为（ ）A ．112B ．114C ．116D ．11816.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70), [70,80),[80,90), [90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为（ ）A ．588B ．480C ．450D ．12017.=++-+++-+1)1(4)1(6)1(4)1(234x x x x （ ）A ．4xB ．4x -C ．1D ．1- 18.若直线m x y l +-=2:与曲线|4|21:2x y C -=有且仅有三个交点，则m 的取值范围是（） A ．)12,12(+- B ．)2,1( C ．)12,1(+ D ．)12,2(+三、解答题（本大题共有5题，满分74分）解答下列各题必须在答题纸相应编号的规定区域写出必要的步骤．19.（12分）求8)32(xx +的二项展开式中的第5项的二项式系数和系数.20.（14分）求半径为10，且与直线07034=-+y x 相切于)10,10(的圆的方程.21.（14分）已知椭圆13422=+y x 上存在两点A 、B 关于直线m x y +=4对称，求m 的取值范围.22.（16分）如图，四棱柱1111D C B A ABCD -中, 侧棱⊥A A 1底面ABCD ，AD AB DC AB ⊥,//， 1==CD AD ，21==AB AA ，E 为棱1AA 的中点.(1) 证明：CE C B ⊥11；(2) 求异面直线E C 1与AD 所成角的大小.（结果用反三角函数值表示）24.（18分）下图是利用计算机作图软件在直角坐标平面xOy 上绘制的一列抛物线和一列直线，在焦点为n F 的抛物线列x p y C n n 4:2=中，n p 是首项和公比都为)10(<<p p 的等比数列，过n F 作斜率2的直线n l 与n C 相交于n A 和n B （n A 在x 轴的上方，n B 在x 轴的下方）.（4）证明：n OA 的斜率是定值；（5）求1A 、2A 、Λ、n A 、Λ所在直线的方程；（6）记n n OB A ∆的面积为n S ，证明：数列}{n S 是等比数列，并求所有这些三角形的面积的和.第23题图第二学期高二年级数学学科期末考试卷参考答案19.（12分）解：4485)32)((x x C T =， 所以二项式系数为7048=C ，系数为811120.22.（14分）解：设直线AB 方程为b x y +-=4，联立 ⎪⎩⎪⎨⎧+-==+,4,124322b x y y x 得,0481681322=-+-b bx x 从而,138b x x B A =+ ,13242)(41b b x x y y B A B A =++-=+则B A ,中点是)1312,134(b b， 则,013121344=+-⋅m b b 解得.134b m -= 由0481681322=-+-b bx x 有实数解得,0)4816(526422≥--=∆b b 即.4132≤b 于是.413)413(2≤-m 则m 的取值范围是.1313213132≤≤-m24.（18分）解：（1）由已知得n n p p =，抛物线焦点)0,(n n p F ，抛物线方程为x p y n42=，直线n l 的方程为).(2np x y -=于是，抛物线n C 与直线n l 在x 轴上方的交点),(11y x A n 的坐标满足⎪⎩⎪⎨⎧-==),(2,411121nnp x y x p y 则有,042211121=-+x y x y 而直线n OA 的斜率为11x y k n OA =，则,042112=-+OA OA k k 解得,51±-=n OA k 又,0>k 点n A 在第一象限，则51+-=n OA k ； （4）直线方程为x y )51(+-=；（5）由⎪⎩⎪⎨⎧-==),(2,42nn p x y x p y 得,04222=--n n p y p y 则np AB 10||=，而O 到直线n l 的距离为52np ，于是n n OB A ∆的面积nn pS 252=，所以数列}{n S 是以252p 为首项，2p 为公比的等比数列.由于10<<p ，所以所有三角形面积和为22152pp -.上海市高二年级第二学期数学学科期终考试试卷（注意事项：本试卷共2页，满分100分，答题时间90分钟。

宝山区2017学年第二学期期末高二年级数学学科教学质量监测试卷（120分钟，150分） 2018.6一、填空题（本大题满分54分）本大题共有12题，1-6题每题4分，7-12题每题5分。

1、在复数范围内，方程012=++x x 的根为2、若直线l 经过点()1,1-A ，且一个法向量为()3,3=→n ，则直线l 的方程是 3、行列式570463132-的第2行第3列元素的代数余子式23M 的值为4、在直角ABC ∆中， 90=∠C ， 30=∠A ，1=BC ，D 为斜边AB 的中点，则=⋅→→CD AB5、执行右图的程序框图，如果输入6=i ，则输出的S 的值为6、在数列{}n a 中，()()⎪⎪⎩⎪⎪⎨⎧-=是偶数，是奇数n n a nnn 52,51，n n a a a S 2212...+++=，则=∞→n n S 2lim 7、若不论k 为何实数，直线1+=kx y 与曲线0422222=--+-+a a ax y x 恒有公共点，则实数a 的取值范围是8、已知线段AB 长为3，A 、B 两点到平面α的距离分别为1与2，则AB 所在直线与平面α所成角的大小为9、若420=-+-z z i z 表示的动点的轨迹是椭圆，则0z 的取值范围是10、将一个半径为1和2的两个铅球，溶成一个大铅球，那么，这个大铅球的表面积是 11、设⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=∈⎪⎪⎭⎫ ⎝⎛=c b R d c b a d c b a S ,,,,1，⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=+==∈⎪⎪⎭⎫ ⎝⎛=0,,,,2c b d a R d c b a d c b a S ，已知矩阵B A +=⎪⎪⎭⎫ ⎝⎛8642，其中1S A ∈，2S B ∈，那么=B12、一只酒杯的轴截面是抛物线的一部分，它的函数解析式()20022≤≤=y x y ，在杯内放一个玻璃球，要使球触及酒杯底部，则玻璃球的半径r 的取值范围是二、选择题（本大题满分20分），本大题共有4题，每题5分13、下列四个命题中真命题是（ ）A . 垂直于同一直线的两条直线互相平行；B . 底面各边相等、侧面都是矩形的四棱柱是正四棱柱；C . 过空间任一点与两条异面直线都垂直的直线有且只有一条；D . 过球面上任意两点的大圆有且只有一个.14、设2018432....i i i i M ++++=，2018432....i i i i N ⋅⋅⋅=，i 为虚数单位，则M 与N 的关系是（ ）A . 0=+N MB . N M <C . N M >D . N M =15、设→→b a ,均是非零向量，且→→=b a 2，若关于x 的方程02=⋅++→→→b a x a x 有实根，则→a 与→b 的夹角的取值范围为（ ）A . ⎥⎦⎤⎢⎣⎡6,0πB . ⎥⎦⎤⎢⎣⎡ππ,3C . ⎥⎦⎤⎢⎣⎡32,3ππD . ⎥⎦⎤⎢⎣⎡ππ,6 16、定义：如果一个向量列从第二项起，每一项与它的前一项的差都等于同一个常向量，那么这个向量列叫做等差向量列，这个常向量叫做等差向量列的公差。

七宝中学高二月考数学试卷2017。

10一. 填空题1。

已知(2014,2017)OA =，(2015,2016)OB =,则||AB = 2. 等差数列{}na 的前n 项和为nS ，则12lim(32)nn n nS n S →∞+=+3. 已知正△ABC 的面积是43AB BC ⋅=4。

已知(1,)a k =,(2,2)b =-(0)k >，若()()a b a b +⊥-,则正数k =5。

已知Rt △ABC 的内角A 、B 、C 所对的边分别是a 、b 、c ，若A 、B 、C 依次成等差数列，且A B C <<，则::a b c = 6. 设等比数列{}na 的公比为2,前n项和为nS ，则44S a =7。

若三点(2,2)A ，(,0)B a ，(0,4)C ，若存在实数λ，使得AB BC λ=，则实数a =8。

已知8,1821(),92n n nn a n -⎧≤≤⎪⎪=⎨⎪≥⎪⎩ *()n N ∈,则12lim()n n a a a →∞++⋅⋅⋅+=9。

已知等差数列{}n a 的公差不为零，且51020n m a a a a -+=+*(,)m n N ∈,则mn 的最大值 是10。

设两向量1e 、2e ,满足1||2e =，2||1e=，它们的夹角为60°,若向量1227te e +与向量12e te +夹角为钝角,则实数t 的取值范围是11。

设a 、b 、c 都是非零向量，其中任意两个都不平行，已知()a b +//c ，a //()b c +，则关于x 的方程()a c x b +=的解x =12. 给定平面上四点O 、A 、B 、C 满足4OA =，3OB =,2OC =,3OB OC ⋅=，则△ABC面积的最大值为二. 选择题13。

已知1-、a 、x 、b 、9-依次成等比数列,则实数x 的值为（ ） A 。

3 B 。

3-C. 3或3- D 。