凹形竖曲线新计算
- 格式：xls
- 大小：19.00 KB
- 文档页数：2
下载文档原格式
合集下载
竖曲线计算公式
然后根据R=5000m和相应的桩距xi,即可求得竖曲线上各桩的标高改正数yi,计算结果列表
桩号
至起点或终点距离
xi
标高改正值
Yi
坡道高成
竖曲线高成
备注
1+638.3
48.95
48.95
竖曲线起点
1+650
X1=11.7
Y1=0.01
48.82
48.83
i1=－1.114％
1+660
X2=21.7
Y2=0.05
T=1/2*R*(i1-i2)
L=R(i1-i2)
E=T2/2*R
yi=x2i/2R (yi在凹形曲线中为正号，凸型曲线中为负号)
例：设i1=－1.114％，i2=+0.154％，为凹型曲线，变坡点的桩号为1+670，高成为48.60m，预设置R=5000m的曲线，求各测设元素、起点、终点的桩号和高成，曲线上每10m间距里程的标高改正数和设计高成。
48.71
48.76
1+670
X3=31.7
E=0.10
48.60
48.70
变坡点
1+680
X4=21.7
Y2=0.05
48.62
48.67
i2=+0.154％
1+690
X5=11.7
Y1=0.01
48.63
48.64
1+701.7
48.65
48.65
竖曲线终点
按上列公式求得T=31.70m，L=63.40m, E=0.10m,竖曲线起点、终点的桩号和高成为
起点桩号= 1+(670－31.70)=1+638.30
桩号
至起点或终点距离
xi
标高改正值
Yi
坡道高成
竖曲线高成
备注
1+638.3
48.95
48.95
竖曲线起点
1+650
X1=11.7
Y1=0.01
48.82
48.83
i1=－1.114％
1+660
X2=21.7
Y2=0.05
T=1/2*R*(i1-i2)
L=R(i1-i2)
E=T2/2*R
yi=x2i/2R (yi在凹形曲线中为正号，凸型曲线中为负号)
例：设i1=－1.114％，i2=+0.154％，为凹型曲线，变坡点的桩号为1+670，高成为48.60m，预设置R=5000m的曲线，求各测设元素、起点、终点的桩号和高成，曲线上每10m间距里程的标高改正数和设计高成。
48.71
48.76
1+670
X3=31.7
E=0.10
48.60
48.70
变坡点
1+680
X4=21.7
Y2=0.05
48.62
48.67
i2=+0.154％
1+690
X5=11.7
Y1=0.01
48.63
48.64
1+701.7
48.65
48.65
竖曲线终点
按上列公式求得T=31.70m，L=63.40m, E=0.10m,竖曲线起点、终点的桩号和高成为
起点桩号= 1+(670－31.70)=1+638.30
竖曲线计算
竖曲线竖曲线在线路纵断面上，以变坡点为交点，连接两相邻坡段的曲线称为竖曲线。
竖曲线有凸形和凹形两种。
道路纵断面线形常采用直线(又叫直坡段)、竖曲线两种线形，二者是纵断面线形的基本要素。
竖曲线常采用抛物线，因为在设计和计算上，抛物线比圆曲线更方便。
在道路纵断面上两个相邻纵坡线的交点，被称为变坡点。
为了保证行车安全、舒适以及视距的需要，在变坡处设置竖曲线。
竖曲线的主要作用是：缓和纵向变坡处行车动量变化而产生的冲击作用，确保道路纵向行车视距；将竖曲线与平曲线恰当地组合，有利于路面排水和改善行车的视线诱导和舒适感。
竖曲线技术指标主要有竖曲线半径和竖曲线长度。
凸形的竖曲线的视距条件较差，应选择适当的半径以保证安全行车的需要。
凹形的竖曲线，视距一般能得到保证，但由于在离心力作用下汽车要产生增重，因此应选择适当的半径来控制离心力不要过大，以保证行车的平顺和舒适。
凹形竖曲线最小半径为100M,凸形竖曲线为300M.拉坡后，坡度差已知，变坡点高程已知，切线上各点和高程也就知道了。
选定竖曲线半径R ，用竖距计算公式求出切线上各点的竖距，切线高程减竖距就是竖曲线高程。
竖距公式如下：h=距离的平方除以两倍的半径.纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状，通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。
一、竖曲线如图所示，设相邻两纵坡坡度分别为i 1 和i 2，则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ，其中i 1、i 2为本身之值，当上坡时取正值，下坡时取负值。
当 i 1- i 2为正值时，则为凸形竖曲线。
当 i 1 - i 2 为负值时，则为凹形竖曲线。
（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
凸形、凹形竖曲线高程计算表
i1-i2
-0.050
凹曲线
点号 计算桩号
1 4956.469 2 4958.469 3 4960.469 4 4962.469 5 4964.469 6 4966.469 7 4967.000 8 4968.469 9 4970.469 10 4972.469
K4+956.469～K4+977.531m竖曲线范围内各点高程 凸形竖曲线
曲线中点 桩号
桩号差L
变坡点 高程Hz
半 径R
i1
1
10150.000 10200.000
-50
7.200
4000.000
0.01
2
10175.000 10200.000
-25
7.200
4000.000
0.01
3
10200.000 10200.000
0
7.200
4000.000
0.01
4
10225.000 10200.000
第一坡度i1 -0.032
第一坡度i2 切线长T 外矢距E 外矢距E 0.017967 12.49175 0.15604 0.156044
x
y=x2/2R
10.000
0.1
验算的过程
切线高程
待计算点高程 验算
1610.740744 1610.840744
备注
12.492 0.1560501 1610.661
4967.000 3.469 1611.200 600.000 0.017967 -0.017137 1611.099
4967.000 5.469 1611.200 600.000 0.017967 -0.017137 1611.085
竖曲线计算原理
式中： 式中：R——抛物线顶点 抛物线顶点 处的曲率半径
A
B
一、竖曲线要素的计算公式 竖曲线的基本方程式： 1．竖曲线的基本方程式：设变坡点相邻两纵坡坡 度分别为i 抛物线竖曲线有两种可能的形式： 度分别为i1和i2。抛物线竖曲线有两种可能的形式： 包含抛物线底（ （1）包含抛物线底（顶）部； 不含抛物线底（ （2）不含抛物线底（顶）部。
2．时间行程不过短 ．时间行程不过短 最短应满足3 行程。 最短应满足3s行程。
Lmin V V = t= 3.6 1.2 则 Rmin V = = ω 1.2ω L min
3．满足视距的要求： 满足视距的要求： 凸形竖曲线： 凸形竖曲线：坡顶视线受阻 凹形竖曲线： 凹形竖曲线：下穿立交 4. 凸形竖曲线主要控制因素：行车视距。 凸形竖曲线主要控制因素：行车视距。 凹形竖曲线的主要控制因素：缓和冲击力。 凹形竖曲线的主要控制因素：缓和冲击力。
1 2 y= x + i1 x 2k 式中： 式中：k——抛物线顶点 抛物线顶点 处的曲率半径 ；
B
i1——竖曲线顶 竖曲线顶 点处切线的坡度。 （底）点处切线的坡度。
A
对竖曲线上任一点P 其切线的斜率（纵坡） 对竖曲线上任一点P，其切线的斜率（纵坡）为
iP = dy x = + i1 dx k
当x=0时，ip=i1； 时 当x=L时， i = L + i = i 时 p 1 2
T2 Lω Tω E= ，E上任一点竖距 ： ）竖曲线上任一点竖距h：
x2 x2 h = PQ = y P − yQ = + i1 x − i1 x = 2R 2R
下半支曲线在竖曲线终点的切线上的竖距h’ 下半支曲线在竖曲线终点的切线上的竖距 ’为：
竖曲线计算公式
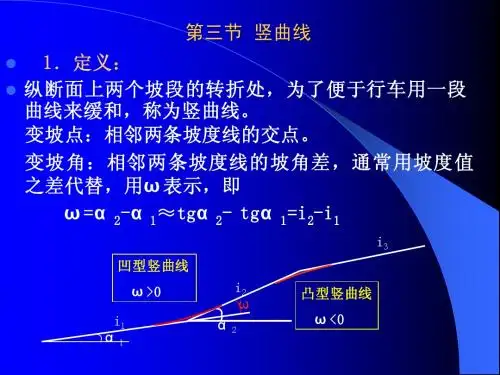
第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。
2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m 桩号k5+000处：x1=k5+000-k4+940=60m切线高程＝423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程＝426.18 - 0.90=425.28m 桩号k5+100处：x２=k5+100-k4+940=160m切线高程＝423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=40米m设计高程＝431.18 - 6.40=424.78m1、在桩号k1+575处，引黄渠提水站一级动力电缆埋设电缆一趟。
其工程做法为：采用3*16加1加k电缆，长70米；外套2寸塑料管70米；现浇C20砼包封30*30cm。
两端接头设1000mm砖砌检查井，井壁厚240mm，钢筋砼圈盖两套。
2、根据运城市规划设计院《关于振西大街设计变更申请的答复意见》第4条，经与建设单位，当地村委会协商，分别在k0+150，k0+320，k0+930四处增设灌渠倒虹吸管，工程做法为：DN600钢筋砼承插口管，橡胶胶圈接口，长54米，四周C20砼封包，厚度30cm，进出水口井为1000cm，深4.1米，收口70cm圆形井，加盖钢筋砼圈盖各一套，内外1：2水泥砂浆抹面，四周3：7灰土夯填，引渠长40米，（梯形（45+30）*40/2cm，现浇砼厚5cm）；C20现浇砼澄泥池70*70*70cm，壁厚20cm。
竖曲线(凹型凸型通用程序)
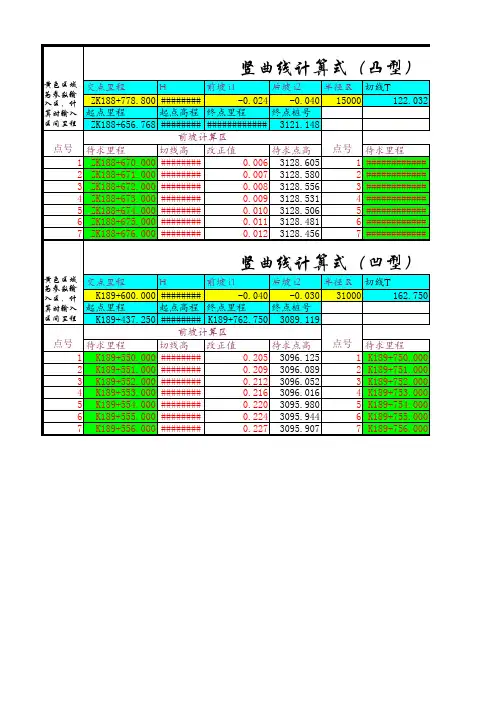
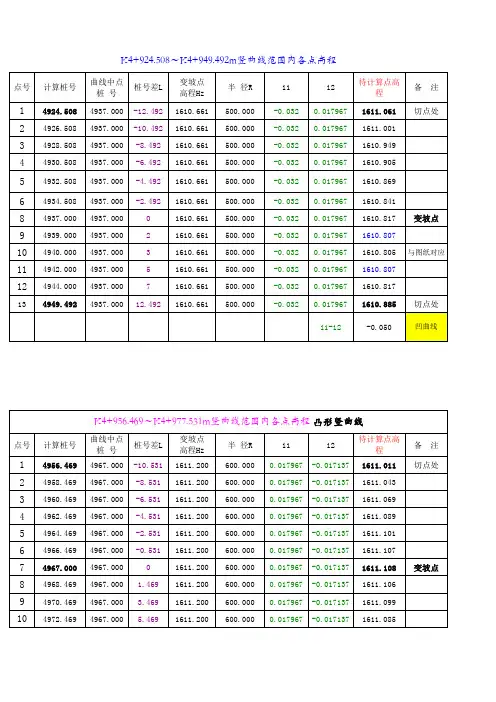
交点里程交点高程H前坡 i1后坡 i2半径 R切线TZK188+778.800########-0.024-0.04015000122.032起点里程起点高程终点里程终点桩号ZK188+656.768####################3121.148
待求里程切线高改正值待求点高程待求里程1ZK188+670.000########0.0063128.6051############2ZK188+671.000########0.0073128.5802############3ZK188+672.000########0.0083128.5563############4ZK188+673.000########0.0093128.5314############5ZK188+674.000########0.0103128.5065############6ZK188+675.000########0.0113128.4816############7ZK188+676.000########0.0123128.4567############
交点里程交点高程H前坡 i1后坡 i2半径 R切线TK189+600.000########-0.040-0.03031000162.750起点里程起点高程终点里程终点桩号K189+437.250########K189+762.7503089.119
待求里程切线高改正值待求点高程待求里程1K189+550.000########0.2053096.1251K189+750.0002K189+551.000########0.2093096.0892K189+751.0003K189+552.000########0.2123096.0523K189+752.0004K189+553.000########0.2163096.0164K189+753.0005K189+554.000########0.2203095.9805K189+754.0006K189+555.000########0.2243095.9446K189+755.0007K189+556.000########0.2273095.9077K189+756.000
竖曲线计算原理
3 / 2 /
d2y dx2
dy d2y 1 i, 2 k dx dx
抛物线上任一点的曲率半径 r = k（1+i2）3/2 竖曲线底部的切线坡度i1 较小，故i12 可略去不 计 ，则竖曲线底部的曲率半径R为： R = r ≈ k
二次抛物线竖曲线基本方程式（通式）为 1 2 y x i1 x 2R
一、竖曲线要素的计算公式
1．竖曲线的基本方程式：设变坡点相邻两纵坡坡 度分别为i1和i2。抛物线竖曲线有两种可能的形式： （1）包含抛物线底（顶）部； （2）不含抛物线底（顶）部。
1 2 y x 2R
式中：R——抛物线顶点 处的曲率半径A NhomakorabeaB
一、竖曲线要素的计算公式
1．竖曲线的基本方程式：设变坡点相邻两纵坡坡 度分别为i1和i2。抛物线竖曲线有两种可能的形式： （1）包含抛物线底（顶）部； （2）不含抛物线底（顶）部。
Lmin V V t 3.6 1.2 则 Rmin V 1.2 L min
3．满足视距的要求： 凸形竖曲线：坡顶视线受阻 凹形竖曲线：下穿立交
4. 凸形竖曲线主要控制因素：行车视距。
凹形竖曲线的主要控制因素：缓和冲击力。
第三节 竖曲线
1．定义： 纵断面上两个坡段的转折处，为了便于行车用一段 曲线来缓和，称为竖曲线。 变坡点：相邻两条坡度线的交点。 变坡角：相邻两条坡度线的坡角差，通常用坡度值 之差代替，用ω 表示，即 ω =α 2-α 1≈tgα 2- tgα 1=i2-i1
i3 凹型竖曲线 ω >0 α i1
x2 x2 h PQ y P yQ i1 x i1 x 2R 2R
竖曲线高程计算公式推导过程及计算流程
竖曲线高程计算公式推导及计算流程1. 竖曲线介绍竖曲线是指在纵断面内，两个坡线之间为了延长行车视距或者减小行车的冲击力，而设计的一段曲线。
一般可以用圆曲线和抛物线来充当竖曲线。
由于圆曲线的计算量较大，所以，通常采用抛物线作为竖曲线，以减少计算量。
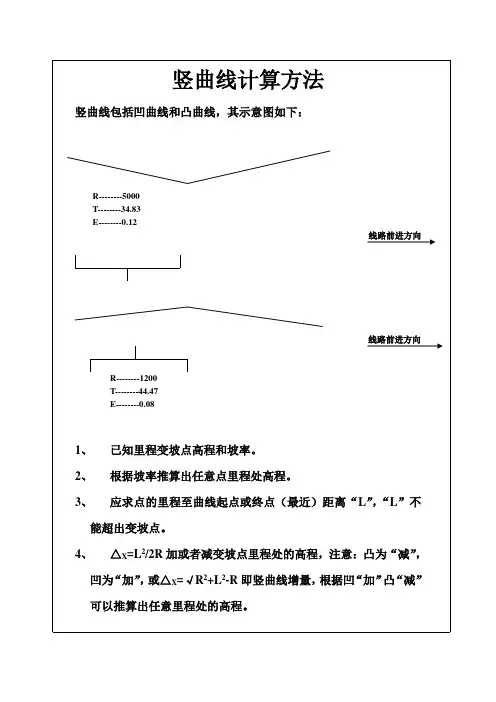
2. 竖曲线高程计算流程竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：a. 计算竖曲线的基本要素：竖曲线长L ；切线长T ；外失距Eb. 计算竖曲线起终点的桩号：竖曲线起点的桩号=变坡点的桩号－Tc. 计算竖曲线上任意点切线标高及改正值： 切线标高=变坡点的标高±（x T -）⨯i 改正值：221x Ry =d. 计算竖曲线上任意点设计标高某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高+ y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－y3. 竖曲线高程计算公式推导已知条件：第一条直线的坡度为1i ，下坡为负值， 第一条直线的坡度为2i ，上坡为正值， 变坡点的里程为K ，高程为H ， 竖曲线的切线长为B A T T T ==, 待求点的里程为X K 曲线半径R竖曲线特点：抛物线的对称轴始终保持竖直，即：X 轴沿水平方向，Y 轴沿竖直方向，从而保证了X 代表平距，Y 代表高程。
抛物线与相邻两条坡度线相切，抛物线变坡点两侧一般不对称，但两切线长相等。
竖曲线高程改正数计算公式推导 设抛物线方程为：()021≠++=a c bx ax y 设直线方程为：()02≠+=k b kx y由图可知，抛物线与直线都经过坐标系222Y O X 的原点2O ,所以可得：00==b c ；分别对21y y 、求导可得：b ax y +=2'1k y ='2当0=x 时，由图可得：b i y ==1'1k i y ==1'2当L x =时，由图可得：12'12i aL i y +==由上式可得：RL L i i a 212212==-=ω 所以抛物线方程为：x i x Ry 12121+=直线方程为：x i y 12=对于竖曲线上任意一点P ，到其切线上Q 点处的竖直距离,即高程改正数y 为：21122121X RX i X i X R y y y P Q =-+=-= 竖曲线曲线元素推导竖曲线元素有切线长T 、外失距E 和竖曲线长L 三个元素，推导过程如下： 由图可知：2tan ω=R T 由于转角ω很小，所以可近似认为22tanωω=，因此可得：2ωR T =由图易得：ωR L = 将切线长T 带入到221x Ry =中可得 外失距RT E 22=4. 曲线高程计算示例已知：某条道路变坡点桩号为K25+460.00，高程为780.72.m ，i1＝0.8％，i2＝5％，竖曲线半径为5000m 。
竖曲线计算方法
=224.656-0.1338
=224.522
切点处K46+325.40的标高为：226.60-75.4×0.054=222.528
K46+286.00处的标高为：222.528+（（325.40-286.00）×0.054）=224.656
△X=L2/2R=39.42/2×5800=0.1338
则：K46+286.00处的设计标高计算为：224.656-△X
3、应求点的里程至曲线起点或终点（最近）距离“L”，“L”不能超出变坡点。
4、△X=L2/2R加或者减变坡点里程处的高程，注意：凸为“减”，凹为“加”，或△X=√R2+L2-R即竖曲线增量，根据凹“加”凸“减”可以推算出任意里程处的高程。
例：
求里程为K46+ቤተ መጻሕፍቲ ባይዱ86处设高程：
R----5800
T-----75.40
E-----0.49
K46+174.60K46+250标高：226.60
K46+286.00
K46+325.40
切点的里程为K46+250+切线长为切线终点里程
即：（K46+250）+75.4（切线长）= K46+325.40
K46+250-切线长为起点里程
即：（K46+250）-75.4（切线长）= K46+174.60
竖曲线计算方法
竖曲线包括凹曲线和凸曲线，其示意图如下：
R--------5000
T--------34.83
E--------0.12
线路前进方向
线路前进方向
R--------1200
=224.522
切点处K46+325.40的标高为：226.60-75.4×0.054=222.528
K46+286.00处的标高为：222.528+（（325.40-286.00）×0.054）=224.656
△X=L2/2R=39.42/2×5800=0.1338
则：K46+286.00处的设计标高计算为：224.656-△X
3、应求点的里程至曲线起点或终点（最近）距离“L”，“L”不能超出变坡点。
4、△X=L2/2R加或者减变坡点里程处的高程，注意：凸为“减”，凹为“加”，或△X=√R2+L2-R即竖曲线增量，根据凹“加”凸“减”可以推算出任意里程处的高程。
例：
求里程为K46+ቤተ መጻሕፍቲ ባይዱ86处设高程：
R----5800
T-----75.40
E-----0.49
K46+174.60K46+250标高：226.60
K46+286.00
K46+325.40
切点的里程为K46+250+切线长为切线终点里程
即：（K46+250）+75.4（切线长）= K46+325.40
K46+250-切线长为起点里程
即：（K46+250）-75.4（切线长）= K46+174.60
竖曲线计算方法
竖曲线包括凹曲线和凸曲线，其示意图如下：
R--------5000
T--------34.83
E--------0.12
线路前进方向
线路前进方向
R--------1200
竖曲线运算步骤及公式讲解
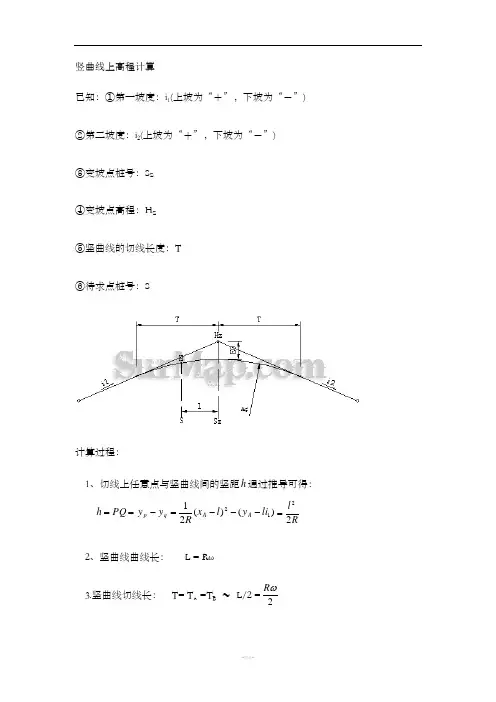
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。
竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。
（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。
竖曲线计算公式
文档仅供参考，不能作为科学依据，请勿模仿；如有不当之处，请联系网站或本 人删除。
（3）凸形竖曲线最小长度 : 竖曲线最小长度相当于各级道路计算行车速度的3秒行程 。
文档仅供参考，不能作为科学依据，请勿模仿；如有不当之处，请联系网站或本 2.凹形竖曲线最小半径和最小长度人删除。
设置凹竖曲线的主要目的：缓和行车时的离心力引起的冲击力。
Lcz-BPDn-1 HT
Hn BPDn
HT
y
in-1
in
Lcz1
HSLcz2
in+1
BPDn-1 Hn-1
文档仅供参考，不能作为科学依据，请勿模仿；如有不当之处，请联系网站或本
（3）逐桩设计高程计算
人删除。
切线高程： H TH n 1 in(L cB zn P 1)D
H TH nin(Lc B z P n)D
4.3.2 竖曲线要素的计算公人式删除。
1．竖曲线的基本方程式： （1）包含抛物线底（顶）部； （2）不含抛物线底（顶）部。
y 1 x2 2R
y
1 x2 2R
i1x
式中：R——抛物线顶点处的曲率半径 ；
i1——竖曲线顶（底）点处切线 的坡度。
B
A
文档仅供参考，不能作为科学依据，请勿模仿；如有不当之处，请联系网站或本
人删除。
4.3.4 逐桩设计高程计算
（1）纵断面设计成果 ➢ 变坡点桩号 BPD ➢ 变坡点设计高程 H ➢ 竖曲线半径 R
（2）竖曲线要素的计算公式
变坡角ω= i2- i1 曲线长：L=Rω 切线长：T=L/2= Rω/2 外 距： E T 2
2R
纵 距： y x 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上一变坡点桩号600上一变坡点高程29.000下一变坡点桩号1480
计算变坡点桩号1220计算变坡点高程23.000
i1-0.0097i20.0038w=i2-i10.0135
竖曲线半径18000.000
竖曲线要素T121.712L243.424E0.411
竖曲线起点桩号1098.288竖曲线终点桩号1341.712
起点高程24.178竖曲线终点高程23.468
所求桩号横距x纵距y切线高程设计高程
1280181.7120.917222.41923.337
1240141.7120.55822.80623.364
1260161.7120.72622.61323.339
下一变坡点高程24.000