初二数学面积法几何专题

初 二 数 学 - - - 面 积 法 解 题【本讲教育信息 】【解说内容】——如何证明面积问题以及用面积法解几何问题【教课目的】1. 使学生灵巧掌握证明几何图形中的面积的方法。

2. 培育学生剖析问题、解决问题的能力。

【要点、难点】：要点：证明面积问题的理论依照和方法技巧。

难点：灵巧运用所学知识证明面积问题。

【教课过程】（一）证明面积问题常用的理论依照1. 三角形的中线把三角形分红两个面积相等的部分。

2. 同底同高或等底等高的两个三角形面积相等。

3. 平行四边形的对角线把其分红两个面积相等的部分。

4. 同底（等底）的两个三角形面积的比等于高的比。

同高（或等高）的两个三角形面积的比等于底的比。

5. 三角形的面积等于等底等高的平行四边形的面积的一半。

8. 有一个角相等或互补的两个三角形的面积的比等于夹角的两边的乘积的比。

（二）证明面积问题常用的证题思路和方法1. 分解法：往常把一个复杂的图形，分解成几个三角形。

2. 作平行线法：经过平行线找出同高（或等高）的三角形。

3. 利用相关性质法：比方利用中点、中位线等的性质。

4. 还能够利用面积解决其余问题。

【典型例题】（一）如何证明面积问题1. 分解法例 1. 从△ ABC 的各极点作三条平行线 AD 、BE 、CF ，各与对边或延伸线交于 D 、E 、F ，求证：△ DEF 的面积＝ 2△ABC 的面积。

剖析： 从图形上察看，△ DEF 可分为三部分，此中①是△ ADE ，它与△ ADB 同底等 高，故 S ADE S ADB③三是△ AEF ，只需再证出它与△ ABC 的面积相等即可由 S △CFE ＝ S △CFB故可得出 S△AEF＝S△ABC证明：∵ AD//BE//CF∴△ ADB和△ ADE同底等高∴S△ADB＝S△ADE同理可证： S△ADC＝S△ADF∴S△ABC＝S△ADE+S△ADF又∵ S△CEF＝S△CBF∴S△ABC＝S△AEF∴S△AEF+S△ADE+S△ADF＝2S△ABC∴S△DEF＝2S△ABC2.作平行线法例 2. 已知：在梯形 ABCD中， DC//AB， M为腰 BC上的中点剖析：由 M 为腰 BC的中点可想到过 M作底的平行线 MN，则 MN 为此中位线，再利用平行线间的距离相等，设梯形的高为h证明：过 M作 MN//AB∵M为腰 BC的中点∴MN是梯形的中位线设梯形的高为 h（二）用面积法解几何问题有些几何问题，常常能够用面积法来解决，用面积法解几何问题常用到以下性质：性质1：等底等高的三角形面积相等性质 2：同底等高的三角形面积相等性质 3：三角形面积等于与它同底等高的平行四边形面积的一半性质 4：等高的两个三角形的面积比等于底之比性质 5：等底的两个三角形的面积比等于高之比1. 证线段之积相等例 3. 设 AD、BE和 CF是△ ABC的三条高，求证： AD·BC＝BE·AC ＝CF·AB剖析：从结论可看出， AD、BE、CF分别是 BC、AC、AB三边上的高，故可联想到可用面积法。

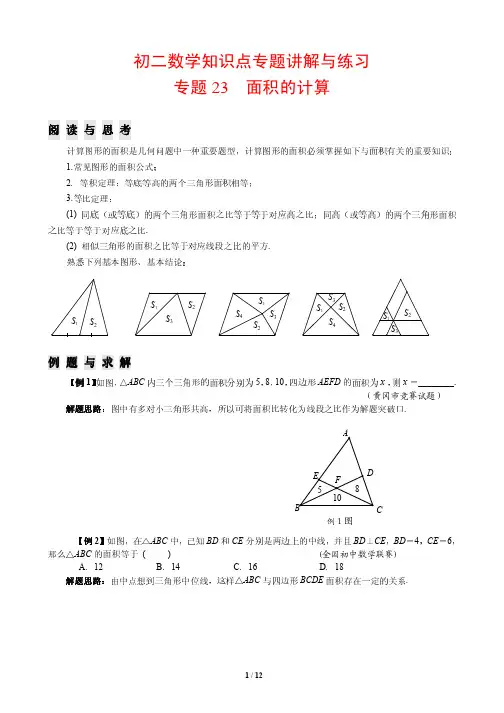
专题27 面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要，面积关联着几何图形的重要元素边与角．所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法．有许多数学问题，虽然题目中没有直接涉及面积，但由于面积联系着几何图形的重要元素，所以借助于有关面积的知识求解，常常简捷明快．用面积法解题的基本思路是：对某一平面图形面积，采用不同方法或从不同角度去计算，就可得到一个含边或角的关系式，化简这个面积关系式就可得到求解或求证的结果．下列情况可以考虑用面积法：（1）涉及三角形的高、垂线等问题；（2）涉及角平分线的问题．例题与求解【例1】如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的边长为______________．(全国初中数学联赛试题) 解题思路：从寻求三条垂线段与等边三角形的高的关系入手．等腰三角形底边上任一点到两腰距离之和等于一腰上的高，那么等边三角形呢？等腰梯形呢？【例2】如图，△AOB中，∠O＝，OA＝OB，正方形CDEF的顶点C在DA上，点D在OB上，点F在AB上，如果正方形CDEF的面积是△AOB的面积的，则OC：OD等于( )A．3：1 B．2：1C．3：2 D．5：3解题思路：由面积关系，可能想到边、角之间的关系，这时通过设元，即可把几何问题代数化来解决．【例3】如图，在□ABCD中，E为AD上一点，F为AB上一点，且BE＝DF，BE与DF 交于G，求证：∠BGC＝∠DGC.（长春市竞赛试题）解题思路：要证∠BGC＝∠DGC，即证CG为∠BGD的平分线，不妨用面积法寻找证题的突破口．【例4】如图，设P为△ABC内任意一点，直线AP，BP，CP交BC，CA，AB于点D、E、F.求证：（1）；（2）. （南京市竞赛试题）解题思路：过P点作平行线，产生比例线段.【例5】如图，在△ABC中，E，F，P分别在BC，CA，AB上，已知AE，BF，CP相交于一点D，且，求的值.解题思路：利用上例的结论，通过代数恒等变形求值.（黄冈市竞赛试题）【例6】如图，设点E，F，G，H分别在面积为1的四边形ABCD的边AB，BC，CD，DA 上，且（是正数），求四边形EFGH的面积．（河北省竞赛试题）解题思路：连对角线，把四边形分割成三角形，将线段的比转化为三角形的面积比．线段比与面积比的相互转化，是解面积问题的常用技巧．转化的基本知识有：(1) 等高三角形面积比，等于它们的底之比；(2) 等底三角形面积比，等于它们的高之比；(3) 相似三角形面积比，等于它们相似比的平方．能力训练1．如图，正方形ABCD的边长为4cm，E是AD的中点，BM⊥EC，垂足为M，则BM＝______.（福建省中考试题）2．如图，矩形ABCD中，P为AB上一点，AP＝ 2BP，CE⊥DP于E，AD＝，AB＝，则CE＝__________.（南宁市中考试题）第1题图第2题图第3题图3．如图，已知八边形ABCDEFGH中四个正方形的面积分别为25，48，121，114，PR＝13，则该八边形的面积为____________.（江苏省竞赛试题）4. 在△ABC中，三边长为，，，表示边上的高的长，，的意义类似，则(＋＋)的值为____________. （上海市竞赛试题）5．如图，△ABC的边AB＝2，AC＝3，Ⅰ，Ⅱ，Ⅲ分别表示以AB，BC，CA为边的正方形，则图中三个阴影部分的面积之和的最大值是__________.（全国竞赛试题）6．如图，过等边△ABC内一点P向三边作垂线，PQ＝6，PR＝8，PS＝10，则△ABC的面积是 ( )．A. B. C. D.（湖北省黄冈市竞赛试题）第5题图第6题图第7题图7．如图，点D是△ABC的边BC上一点，若∠CAD＝∠DAB＝，AC＝3，AB＝6，则AD的长是( )．A．2 B. C.3 D.8．如图，在四边形ABCD中，M，N分别是AB，CD的中点，AN，BN，DM，CM划分四边形所成的7个区域的面积分别为，，，，，，，那么恒成立的关系式是( )．A. +=B.+=C. += D．+=9．已知等边△ABC和点P，设点P到△ABC三边AB，AC，BC的距离分别为，，，△ABC的高为．若点P在一边BC上（如图1），此时，可得结论：＋＋＝.请直接用上述信息解决下列问题：当点P在△ABC内（如图2）、点P在△ABC外（如图3）这两种情况时，上述结论是否还成立？若成立．请给予证明；若不成立，，，与之间又有怎样的关系？请写出你的猜想，不需证明．（黑龙江省中考试题）10.如图，已知D，E，F分别是锐角△ABC的三边BC，CA，AB上的点，且AD、BE、CF 相交于P点，AP＝BP＝CP＝6，设PD＝，PE＝，PF＝，若，求的值．（“希望杯”邀请赛试题）11.如图，在凸五边形ABCDE中，已知AB∥CE，BC∥AD，BE∥CD，DE∥AC，求证：AE∥BD.（加拿大数学奥林匹克试题）12.如图，在锐角△ABC中，D，E，F分别是AB，BC，CA边上的三等分点. P，Q，R分别是△ADF，△BDE，△CEF的三条中线的交点.(1) 求△DEF与△ABC的面积比；(2) 求△PDF与△ADF的面积比；(3) 求多边形PDQERF与△ABC的面积比.13．如图，依次延长四边形ABCD的边AB，BC，CD，DA至E，F，G，H，使，若，求的值．（上海市竞赛试题）14.如图，一直线截△ABC的边AB，AC及BC的延长线分别交于F，E，D三点，求证：．（梅涅劳斯定理）15．如图，在△ABC中，已知，求的值.（“华罗庚金杯”少年数学邀请赛试题）。

初中数学几何图形面积求法最全总结
几何问题一直都是中学数学阶段的一大重点，不仅仅在初中，在高中数学学习中也占有很大比例，所以要学好几何，基础很重要。

在初中数学几何问题中，有时候图形是不规则的，它是由一些基本图形组合、拼凑而成的，对于这类不规则图形，考试经常考的就是求该图形的面积或阴影部分的面积。

公式法
这是最简单，最基础的一种方法，当所求图形是我们常规的几何图形，例如三角形、正方形等。

此时直接运用公式即可。

例如：
和差法
和差法比公式法略微复杂，需要学生进行简单的判断，不过一般难度不大，只需学生用两个或多个常见的几何图形面积进行加减。

1.直接和差法
2.构造和差法
在构造和差法中，通常需要学生构建自己的数学图形转化思维，学会通过添加辅助线求解。

割补法
割补法，是学生拥有比较强的转化能力后才能轻松运用的，否则学生看到这样的题目还是会无从下手。

尤其适用于直接求面积较复杂或无法计算时，通过对图形的平移、旋转、割补等，为利用公式法或和差法求解创造条件。

1.全等法
2.对称法
3.平移法
4.旋转法
当然在实际问题中，解决方法可能不止这一种，有时我们碰到的问题还需要多种方法结合，这就需要我们熟练掌握多种方法，活学活用。

等面积法例题初二数学（原创版）目录1.等面积法的概念2.等面积法的应用3.初二数学中常见的等面积题目类型4.解决等面积题目的步骤和技巧5.例题解析正文一、等面积法的概念等面积法是一种求解几何问题的方法，主要是通过将复杂的几何问题转化为简单的面积问题，从而简化问题。

等面积法在初二数学中是一个重要的知识点，对于提高学生的几何解题能力有重要作用。

二、等面积法的应用等面积法在初二数学中的应用非常广泛，例如在求解三角形、四边形、圆等几何图形的面积时，都可以运用等面积法。

此外，等面积法还可以用于解决一些复杂的几何组合问题，如求解两个三角形面积之和等于一个矩形面积的问题等。

三、初二数学中常见的等面积题目类型初二数学中常见的等面积题目类型主要包括以下几种：1.已知两个图形的面积，求它们的形状和大小；2.已知一个图形的面积和一个边长，求其他边的长度；3.已知两个图形的边长，求它们的面积和形状；4.求解两个图形面积之和等于一个矩形面积的问题。

四、解决等面积题目的步骤和技巧解决等面积题目一般可以分为以下几个步骤：1.观察题目，找出已知条件和需要求解的问题；2.根据已知条件，运用等面积法将问题转化为面积问题；3.利用相关的几何公式，求解面积问题；4.根据求解的结果，得出结论。

在解决等面积题目时，可以运用一些技巧，如：1.利用相似三角形的面积比等于相似比的平方；2.利用两个三角形共边时，它们的面积和等于共边边上的高的比；3.利用矩形的面积等于长乘以宽。

五、例题解析例题：已知一个矩形的长为 8cm，宽为 6cm，求一个与它等面积的三角形的高。

解：根据等面积法，可知该三角形的面积等于矩形的面积，即S=8*6=48。

由于三角形的面积等于底乘以高的一半，所以可以得出：48=底*高/2，解得高=48*2/底。

由于题目没有给出三角形的底，因此需要进一步求解。

可以利用相似三角形的性质，设该三角形的底为 x，那么根据相似比的平方等于面积比，可得出：x/8=高/6，解得 x=48/5。

八年级数学竞赛例题专题讲解：面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要，面积关联着几何图形的重要元素边与角．所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法．有许多数学问题，虽然题目中没有直接涉及面积，但由于面积联系着几何图形的重要元素，所以借助于有关面积的知识求解，常常简捷明快．用面积法解题的基本思路是：对某一平面图形面积，采用不同方法或从不同角度去计算，就可得到一个含边或角的关系式，化简这个面积关系式就可得到求解或求证的结果．下列情况可以考虑用面积法：（1）涉及三角形的高、垂线等问题；（2）涉及角平分线的问题．例题与求解【例1】如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的边长为______________．(全国初中数学联赛试题) 解题思路：从寻求三条垂线段与等边三角形的高的关系入手．等腰三角形底边上任一点到两腰距离之和等于一腰上的高，那么等边三角形呢？等腰梯形呢？【例2】如图，△AOB中，∠O＝，OA＝OB，正方形CDEF的顶点C在DA上，点D在OB上，点F在AB上，如果正方形CDEF的面积是△AOB的面积的，则OC：OD等于( )A．3：1 B．2：1C．3：2 D．5：3解题思路：由面积关系，可能想到边、角之间的关系，这时通过设元，即可把几何问题代数化来解决．【例3】如图，在□ABCD中，E为AD上一点，F为AB上一点，且BE＝DF，BE与DF交于G，求证：∠BGC＝∠DGC.（长春市竞赛试题）解题思路：要证∠BGC＝∠DGC，即证CG为∠BGD的平分线，不妨用面积法寻找证题的突破口．【例4】如图，设P为△ABC内任意一点，直线AP，BP，CP交BC，CA，AB于点D、E、F.求证：（1）；（2）.（南京市竞赛试题）解题思路：过P点作平行线，产生比例线段.【例5】如图，在△ABC中，E，F，P分别在BC，CA，AB上，已知AE，BF，CP相交于一点D，且，求的值.解题思路：利用上例的结论，通过代数恒等变形求值.（黄冈市竞赛试题）【例6】如图，设点E，F，G，H分别在面积为1的四边形ABCD的边AB，BC，CD，DA上，且（是正数），求四边形EFGH的面积．（河北省竞赛试题）解题思路：连对角线，把四边形分割成三角形，将线段的比转化为三角形的面积比．线段比与面积比的相互转化，是解面积问题的常用技巧．转化的基本知识有：(1) 等高三角形面积比，等于它们的底之比；(2) 等底三角形面积比，等于它们的高之比；(3) 相似三角形面积比，等于它们相似比的平方．能力训练1．如图，正方形ABCD的边长为4cm，E是AD的中点，BM⊥EC，垂足为M，则BM＝______.（福建省中考试题）2．如图，矩形ABCD中，P为AB上一点，AP＝2BP，CE⊥DP于E，AD＝，AB＝，则CE＝__________.（南宁市中考试题）第1题图第2题图第3题图3．如图，已知八边形ABCDEFGH中四个正方形的面积分别为25，48，121，114，PR＝13，则该八边形的面积为____________.（江苏省竞赛试题） 4. 在△ABC中，三边长为，，，表示边上的高的长，，的意义类似，则(＋＋)的值为____________. （上海市竞赛试题）5．如图，△ABC的边AB＝2，AC＝3，Ⅰ，Ⅱ，Ⅲ分别表示以AB，BC，CA为边的正方形，则图中三个阴影部分的面积之和的最大值是__________.（全国竞赛试题） 6．如图，过等边△ABC内一点P向三边作垂线，PQ＝6，PR＝8，PS＝10，则△ABC的面积是 ( )．A. B.C.D.（湖北省黄冈市竞赛试题）第5题图第6题图第7题图7．如图，点D是△ABC的边BC上一点，若∠CAD＝∠DAB＝，AC＝3，AB＝6，则AD的长是( )．A．2 B. C.3 D.8．如图，在四边形ABCD中，M，N分别是AB，CD的中点，AN，BN，DM，CM划分四边形所成的7个区域的面积分别为，，，，，，，那么恒成立的关系式是( )．A.+=B.+=C.+= D．+=9．已知等边△ABC和点P，设点P到△ABC三边AB，AC，BC的距离分别为，，，△ABC的高为．若点P在一边BC上（如图1），此时，可得结论：＋＋＝.请直接用上述信息解决下列问题：当点P在△ABC内（如图2）、点P在△ABC外（如图3）这两种情况时，上述结论是否还成立？若成立．请给予证明；若不成立，，，与之间又有怎样的关系？请写出你的猜想，不需证明．（黑龙江省中考试题）10.如图，已知D，E，F分别是锐角△ABC的三边BC，CA，AB上的点，且AD、BE、CF相交于P点，AP＝BP＝CP＝6，设PD＝，PE＝，PF＝，若，求的值．（“希望杯”邀请赛试题）11.如图，在凸五边形ABCDE中，已知AB∥CE，BC∥AD，BE∥CD，DE∥AC，求证：AE∥BD.（加拿大数学奥林匹克试题）12.如图，在锐角△ABC中，D，E，F分别是AB，BC，CA边上的三等分点. P，Q，R分别是△ADF，△BDE，△CEF的三条中线的交点.(1) 求△DEF与△ABC的面积比；(2) 求△PDF与△ADF的面积比；(3) 求多边形PDQERF与△ABC的面积比.13．如图，依次延长四边形ABCD的边AB，BC，CD，DA至E，F，G，H，使，若，求的值．（上海市竞赛试题）14.如图，一直线截△ABC的边AB，AC及BC的延长线分别交于F，E，D三点，求证：．（梅涅劳斯定理）15．如图，在△ABC中，已知，求的值.（“华罗庚金杯”少年数学邀请赛试题）。

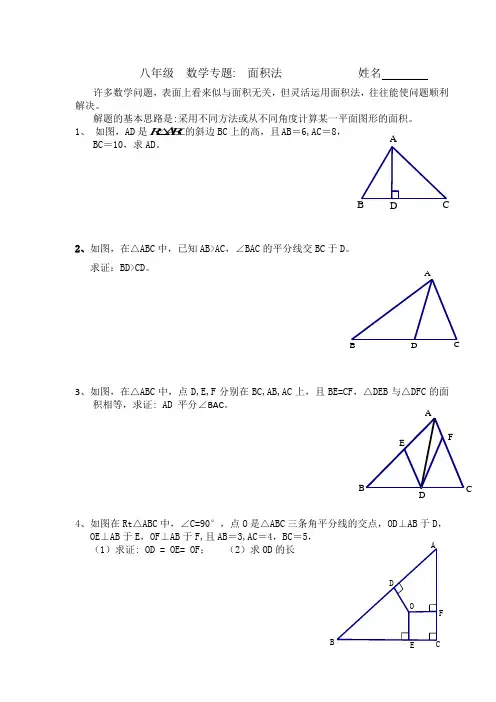
八年级 数学专题: 面积法 姓名许多数学问题，表面上看来似与面积无关，但灵活运用面积法，往往能使问题顺利解决。

解题的基本思路是:采用不同方法或从不同角度计算某一平面图形的面积。

1、 如图，AD 是R t A B C的斜边BC 上的高，且AB ＝6,AC ＝8， BC ＝10，求AD 。

2、如图，在△ABC 中，已知AB>AC ，∠BAC 的平分线交BC 于D 。

求证：BD>CD 。

3、如图，在△ABC 中，点D,E,F 分别在BC,AB,AC 上，且BE=CF ，△DEB 与△DFC 的面积相等，求证: AD 平分∠BAC 。

4、如图在Rt △ABC 中，∠C=90°，点O 是△ABC 三条角平分线的交点，OD ⊥AB 于D ， OE ⊥AB 于E ，OF ⊥AB 于F,且AB ＝3,AC ＝4，BC ＝5，（1）求证: OD = OE= OF ； （2）求OD 的长DFBDCBACBDA5、 如图,在△ABC 中，AB=AC ，点P 是线段BC 上任意一点，PD ⊥AB 于D ，PE ⊥AC 于E ，CF ⊥AB 于F 。

求证：PD+PE=CF 。

归纳：等腰三角形底边上任意一点到两腰的距离之和等于腰上的高。

6、 如图,在△ABC 中，AB=AC ，点P 是线段BC 延长线上任意一点，PD ⊥AB 于D ， PE ⊥AC 于E ，CF ⊥AB 于F 。

求证：PD-PE=CF 。

归纳：等腰三角形底边延长线上任意一点到两腰的距离之差等于腰上的高。

7、如图,在等边△ABC 中，P 为等边△ABC 内的任意一点，PD ⊥BC 于D ， PE ⊥BC 于E ，PF ⊥AC 于F ， AH ⊥BC 于H ，求证：PE+PF+PD= AH归纳：等边三角形内任意一点到三边的距离之和等于等边三角形的高。

8. 如图，AD 是△ABC 的角的平分线，求证：DC BDAC AB =。

9、 如图，在△ABC 中，已知BC 、AC 边上的中线AD 、BF 交于M 。

初二平行四边形面积练习题在初二数学学习中，平行四边形是一个重要的基础概念。

掌握平行四边形的性质和计算其面积的方法，对于进一步学习几何学和解决实际问题都具有重要意义。

本文将为大家提供一些初二平行四边形面积练习题，帮助大家巩固和应用所学知识。

练习题一：计算平行四边形的面积已知平行四边形的底边长为8厘米，高为6厘米，求其面积。

解答：平行四边形的面积可以通过底边长和高的乘积来计算。

根据已知条件，底边长为8厘米，高为6厘米，所以平行四边形的面积S可以计算为：S = 底边长 ×高 = 8厘米 × 6厘米 = 48平方厘米练习题二：计算平行四边形的面积若平行四边形的底边长为12毫米，高为3.5厘米，求其面积。

解答：注意单位转换，底边长的单位为毫米，高的单位为厘米，需要将其转换成相同的单位再进行计算。

底边长为12毫米，转换为厘米为1.2厘米。

平行四边形的面积S可以计算为：S = 底边长 ×高 = 1.2厘米 × 3.5厘米 = 4.2平方厘米练习题三：计算平行四边形的面积已知平行四边形的对角线长度分别为6厘米和8厘米，求其面积。

解答：对角线将平行四边形分成两个相等的三角形，可以利用三角形的面积公式来计算平行四边形的面积。

利用已知信息可知，第一个三角形的底边长度为6厘米，高为8厘米；第二个三角形的底边长度为8厘米，高为6厘米。

可以分别计算两个三角形的面积，然后将两个三角形的面积相加得到平行四边形的面积。

第一个三角形的面积S₁可以计算为：S₁ = 1/2 ×底边长 ×高 = 1/2 × 6厘米 × 8厘米 = 24平方厘米第二个三角形的面积S₂可以计算为：S₂ = 1/2 ×底边长 ×高 = 1/2 × 8厘米 × 6厘米 = 24平方厘米平行四边形的面积S等于两个三角形的面积之和：S = S₁ + S₂ = 24平方厘米 + 24平方厘米 = 48平方厘米通过以上练习题，我们可以发现计算平行四边形的面积主要靠掌握底边长和高或对角线长度的大小，然后利用相应的计算公式进行计算。

初二数学---面积法解题【本讲教育信息】【讲解内容】——怎样证明面积问题以及用面积法解几何问题 【教学目标】1. 使学生灵活掌握证明几何图形中的面积的方法。

2. 培养学生分析问题、解决问题的能力。

【 重点、难点】：重点：证明面积问题的理论依据和方法技巧。

难点：灵活运用所学知识证明面积问题。

【教学过程】（一）证明面积问题常用的理论依据1. 三角形的中线把三角形分成两个面积相等的部分。

2. 同底同高或等底等高的两个三角形面积相等。

3. 平行四边形的对角线把其分成两个面积相等的部分。

4. 同底（等底）的两个三角形面积的比等于高的比。

同高（或等高）的两个三角形面积的比等于底的比。

5. 三角形的面积等于等底等高的平行四边形的面积的一半。

6. 三角形的中位线截三角形所得的三角形的面积等于原三角形面积的。

147. 14三角形三边中点的连线所成的三角形的面积等于原三角形面积的。

8. 有一个角相等或互补的两个三角形的面积的比等于夹角的两边的乘积的比。

（二）证明面积问题常用的证题思路和方法1. 分解法：通常把一个复杂的图形，分解成几个三角形。

2. 作平行线法：通过平行线找出同高（或等高）的三角形。

3. 利用有关性质法：比如利用中点、中位线等的性质。

4. 还可以利用面积解决其它问题。

【典型例题】（一）怎样证明面积问题 1. 分解法例1. 从△ABC 的各顶点作三条平行线AD 、BE 、CF ，各与对边或延长线交于D 、E 、F ，求证：△DEF 的面积＝2△ABC 的面积。

FEAB D C分析：从图形上观察，△DEF 可分为三部分，其中①是△ADE ，它与△ADB 同底等高，故S S ADE ADB ∆∆=②二是△，和上面一样，ADF S S ADF ADC ∆∆=③三是△AEF ，只要再证出它与△ABC 的面积相等即可 由S △CFE ＝S △CFB故可得出S △AEF ＝S △ABC 证明：∵AD//BE//CF∴△ADB 和△ADE 同底等高 ∴S △ADB ＝S △ADE同理可证：S △ADC ＝S △ADF ∴S △ABC ＝S △ADE +S △ADF 又∵S △CEF ＝S △CBF ∴S △ABC ＝S △AEF∴S △AEF +S △ADE +S △ADF ＝2S △ABC ∴S △DEF ＝2S △ABC2. 作平行线法例2. 已知：在梯形ABCD 中，DC//AB ，M 为腰BC 上的中点求证：S S ADM ABCD ∆=12分析：由M 为腰BC 的中点可想到过M 作底的平行线MN ，则MN 为其中位线，再利用平行线间的距离相等，设梯形的高为hA BS S S MN h S AMD DMN AMN ABCD ∆∆∆=+=⋅=1212证明：过M 作MN//AB ∵M 为腰BC 的中点 ∴MN 是梯形的中位线 设梯形的高为hMN DC AB=+2则S MN h ABCD =⋅又 S S S MN h AMD AMN MND ∆∆∆=+=⋅12∴=S S ADM ABCD ∆12（二）用面积法解几何问题有些几何问题，往往可以用面积法来解决，用面积法解几何问题常用到下列性质： 性质1：等底等高的三角形面积相等 性质2：同底等高的三角形面积相等性质3：三角形面积等于与它同底等高的平行四边形面积的一半 性质4：等高的两个三角形的面积比等于底之比性质5：等底的两个三角形的面积比等于高之比 1. 证线段之积相等例3. 设AD 、BE 和CF 是△ABC 的三条高，求证：AD ·BC ＝BE ·AC ＝CF ·ABAFEB D C分析：从结论可看出，AD 、BE 、CF 分别是BC 、AC 、AB 三边上的高，故可联想到可用面积法。

初二数学培优之面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要，面积关联着几何图形的重要元素边与角． 所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法．有许多数学问题，虽然题目中没有直接涉及面积，但由于面积联系着几何图形的重要元素，所以借助于有关面积的知识求解，常常简捷明快．用面积法解题的基本思路是：对某一平面图形面积，采用不同方法或从不同角度去计算，就可得到一个含边或角的关系式，化简这个面积关系式就可得到求解或求证的结果． 下列情况可以考虑用面积法： （1）涉及三角形的高、垂线等问题； （2）涉及角平分线的问题．例题与求解【例1】 如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的边长为______________．(全国初中数学联赛试题)解题思路：从寻求三条垂线段与等边三角形的高的关系入手．等腰三角形底边上任一点到两腰距离之和等于一腰上的高，那么等边三角形呢？等腰梯形呢？B【例2】 如图，△AOB 中，∠O ＝090，OA ＝OB ，正方形CDEF 的顶点C 在DA 上，点D 在OB 上，点F 在AB 上，如果正方形CDEF 的面积是△AOB 的面积的52，则OC ：OD 等于( ) A ．3：1 B ．2：1 C ．3：2 D ．5：3解题思路：由面积关系，可能想到边、角之间的关系，这时通过设元，即可把几何问题代数化来解决．BDC【例3】 如图，在□ABCD 中，E 为AD 上一点，F 为AB 上一点，且BE ＝DF ，BE 与DF 交于G ，求证：∠BGC ＝∠DGC .（长春市竞赛试题）解题思路：要证∠BGC ＝∠DGC ，即证CG 为∠BGD 的平分线，不妨用面积法寻找证题的突破口．B【例4】 如图，设P 为△ABC 内任意一点，直线AP ，BP ，CP 交BC ，CA ，AB 于点D 、E 、F .求证：（1）1=++CF PFBE PE AD PD ； （2）2=++CFPCBE PB AD PA . （南京市竞赛试题） 解题思路：过P 点作平行线，产生比例线段.B【例5】 如图，在△ABC 中，E ，F ，P 分别在BC ，CA ，AB 上，已知AE ，BF ，CP 相交于一点D ，且1994=++DP CD DF BD DE AD ，求DPCDDF BD DE AD ⋅⋅的值. 解题思路：利用上例的结论，通过代数恒等变形求值.（黄冈市竞赛试题）B【例6】如图，设点E ，F ，G ，H 分别在面积为1的四边形ABCD 的边AB ，BC ，CD ， DA 上，且k HADHGD CG FC BF EB AE ====（k 是正数），求四边形EFGH 的面积． （河北省竞赛试题）解题思路：连对角线，把四边形分割成三角形，将线段的比转化为三角形的面积比． 线段比与面积比的相互转化，是解面积问题的常用技巧．转化的基本知识有： (1) 等高三角形面积比，等于它们的底之比； (2) 等底三角形面积比，等于它们的高之比；(3) 相似三角形面积比，等于它们相似比的平方．A能力训练1．如图，正方形ABCD 的边长为4cm ，E 是AD 的中点，BM ⊥EC ，垂足为M ，则BM ＝______.（福建省中考试题）2．如图，矩形ABCD 中，P 为AB 上一点，AP ＝ 2BP ，CE ⊥DP 于E ，AD ＝a ，AB ＝b ，则 CE ＝__________.（南宁市中考试题）PDE第1题图 第2题图 第3题图3．如图，已知八边形ABCDEFGH 中四个正方形的面积分别为25，48，121，114，PR ＝13，则该八边形的面积为____________.（江苏省竞赛试题）4. 在△ABC 中，三边长为3=a ，4=b ，6=c ，a h 表示a 边上的高的长，b h ，c h 的意义类似，则(a h ＋b h ＋c h )⋅⎪⎪⎭⎫⎝⎛++c b ah h h 111的值为____________. （上海市竞赛试题）5．如图，△ABC 的边AB ＝2，AC ＝3，Ⅰ，Ⅱ，Ⅲ分别表示以AB ，BC ，CA 为边的正方形，则图中三个阴影部分的面积之和的最大值是__________.（全国竞赛试题）6．如图，过等边△ABC 内一点P 向三边作垂线，PQ ＝6，PR ＝8，PS ＝10，则△ABC 的面积是 ( )． A. 3192 B. 3190 C. 3194 D.3196（湖北省黄冈市竞赛试题）ERCBBC第5题图 第6题图 第7题图7．如图，点D 是△ABC 的边BC 上一点，若∠CAD ＝∠DAB ＝060，AC ＝3，AB ＝6，则AD 的长是( )．A ．2 B. 212C.3D. 213 8．如图，在四边形ABCD 中，M ，N 分别是AB ，CD 的中点，AN ，BN ，DM ，CM 划分四边形所成的7个区域的面积分别为1S ，2S ，3S ，4S ，5S ，6S ，7S ，那么恒成立的关系式是( )． A. 2S +6S =4S B.1S +7S =4SC. 2S +3S =4S D ．1S +6S =4SDC9．已知等边△ABC 和点P ，设点P 到△ABC 三边AB ，AC ，BC 的距离分别为1h ，2h ，3h ，△ABC 的高为h ．若点P 在一边BC 上（如图1），此时03=h ，可得结论：1h ＋2h ＋3h ＝h .请直接用上述信息解决下列问题：当点P 在△ABC 内（如图2）、点P 在△ABC 外（如图3）这两种情况时，上述结论是否还成立？若成立．请给予证明；若不成立，1h ，2h ，3h 与h 之间又有怎样的关系？请写出你的猜想，不需证明．（黑龙江省中考试题）图3图2图1BBB10.如图，已知D ，E ，F 分别是锐角△ABC 的三边BC ，CA ，AB 上的点，且AD 、BE 、CF 相交于P 点，AP ＝BP ＝CP ＝6，设PD ＝x，PE ＝y ，PF ＝z ，若28=++zx yz xy ，求xyz 的值．（“希望杯”邀请赛试题）B11.如图，在凸五边形ABCDE 中，已知AB ∥CE ，BC ∥AD ，BE ∥CD ，DE ∥AC ，求证：AE ∥BD .（加拿大数学奥林匹克试题）BB 12.如图，在锐角△ABC 中，D ，E ，F 分别是AB ，BC ，CA 边上的三等分点. P ，Q ，R 分别是△ADF ，△BDE ，△CEF 的三条中线的交点.(1) 求△DEF 与△ABC 的面积比；(2) 求△PDF 与△ADF 的面积比；(3) 求多边形PDQERF 与△ABC 的面积比.13．如图，依次延长四边形ABCD 的边AB ，BC ，CD ，DA 至E ，F ，G ，H ，使m DAAHCD DG BC CF AB BE ====，若ABCD EFGH S S 四边形四边形2=，求m 的值． （上海市竞赛试题）G14. 如图，一直线截△ABC 的边AB ，AC 及BC 的延长线分别交于F ，E ，D 三点，求证：1=⋅⋅FBAFEA CE DC BD ． （梅涅劳斯定理）BD15．如图，在△ABC 中，已知21===FA FB EC EA DB DC ，求ABC GHI S S ∆∆的值.（“华罗庚金杯”少年数学邀请赛试题）B。

等面积法例题初二数学摘要：一、等面积法基本概念1.等面积法的定义2.等面积法在初二数学中的应用二、等面积法例题解析1.例题一1.题目描述2.解题思路3.解题步骤2.例题二1.题目描述2.解题思路3.解题步骤3.例题三1.题目描述2.解题思路3.解题步骤三、等面积法在数学中的意义1.等面积法在几何证明中的应用2.等面积法在实际问题中的应用四、等面积法的学习方法与技巧1.掌握基本概念2.多做例题练习3.培养空间想象力正文：一、等面积法基本概念等面积法，是数学中一种常用的解题方法。

它是指在解决数学问题时，如果已知两个或多个图形的面积相等，那么可以通过面积相等这一条件，推导出其他相关量之间的关系。

在初二数学中，等面积法常常应用于几何证明和实际问题解决。

二、等面积法例题解析为了更好地理解等面积法的应用，我们通过以下三个例题来进行解析：例题一：已知矩形ABCD的面积为12平方厘米，矩形EFGH的面积为6平方厘米，若矩形ABCD与矩形EFGH的长和宽之和相等，求矩形ABCD与矩形EFGH的长和宽。

解题思路：由于已知矩形ABCD与矩形EFGH的面积之和，我们可以利用等面积法，设矩形ABCD的长为x，宽为y，矩形EFGH的长为a，宽为b，则有xy=ab=12和x+y=a+b。

通过解这个方程组，我们可以求得矩形ABCD与矩形EFGH的长和宽。

解题步骤：1.根据已知条件列出方程组：xy=12, x+y=a+b2.将第一个方程变形得到：y=12/x，代入第二个方程得到：x+12/x=a+b3.化简得到：x^2-ab+12=04.求解得到：x=2, y=6, a=3, b=2所以，矩形ABCD的长为2厘米，宽为6厘米，矩形EFGH的长为3厘米，宽为2厘米。

例题二：已知等腰三角形ABC，底边BC=6厘米，高AD=8厘米，求等腰三角形ABC的面积。

解题思路：由于已知等腰三角形ABC的底边和高，我们可以利用等面积法，设等腰三角形ABC的腰长为x，则有x^2=8^2+(6/2)^2=64+9=73。

专题27 面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要，面积关联着几何图形的重要元素边与角．所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法．有许多数学问题，虽然题目中没有直接涉及面积，但由于面积联系着几何图形的重要元素，所以借助于有关面积的知识求解，常常简捷明快．用面积法解题的基本思路是：对某一平面图形面积，采用不同方法或从不同角度去计算，就可得到一个含边或角的关系式，化简这个面积关系式就可得到求解或求证的结果． 下列情况可以考虑用面积法：（1）涉及三角形的高、垂线等问题； （2）涉及角平分线的问题．例题与求解【例1】 如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的边长为______________．(全国初中数学联赛试题)解题思路：从寻求三条垂线段与等边三角形的高的关系入手．等腰三角形底边上任一点到两腰距离之和等于一腰上的高，那么等边三角形呢？等腰梯形呢？DEFA BC P【例2】 如图，△AOB 中，∠O ＝090，OA ＝OB ，正方形CDEF 的顶点C 在DA 上，点D 在OB 上，点F 在AB 上，如果正方形CDEF 的面积是△AOB 的面积的52，则OC ：OD 等于( ) A ．3：1 B ．2：1 C ．3：2 D ．5：3解题思路：由面积关系，可能想到边、角之间的关系，这时通过设元，即可把几何问题代数化来解决．EFAOBDC【例3】 如图，在□ABCD 中，E 为AD 上一点，F 为AB 上一点，且BE ＝DF ，BE 与DF 交于G ，求证：∠BGC ＝∠DGC .（长春市竞赛试题）解题思路：要证∠BGC ＝∠DGC ，即证CG 为∠BGD 的平分线，不妨用面积法寻找证题的突破口．GDBC A F E【例4】 如图，设P 为△ABC 内任意一点，直线AP ，BP ，CP 交BC ，CA ，AB 于点D 、E 、F .求证：（1）1=++CF PFBE PE AD PD ； （2）2=++CFPCBE PB AD PA . （南京市竞赛试题）解题思路：过P 点作平行线，产生比例线段.EPBAC DF【例5】 如图，在△ABC 中，E ，F ，P 分别在BC ，CA ，AB 上，已知AE ，BF ，CP 相交于一点D ，且1994=++DP CD DF BD DE AD ，求DPCDDF BD DE AD ⋅⋅的值. 解题思路：利用上例的结论，通过代数恒等变形求值.（黄冈市竞赛试题）FDABC EP【例6】如图，设点E ，F ，G ，H 分别在面积为1的四边形ABCD 的边AB ，BC ，CD ， DA上，且k HADHGD CG FC BF EB AE ====（k 是正数），求四边形EFGH 的面积． （河北省竞赛试题）解题思路：连对角线，把四边形分割成三角形，将线段的比转化为三角形的面积比． 线段比与面积比的相互转化，是解面积问题的常用技巧．转化的基本知识有： (1) 等高三角形面积比，等于它们的底之比； (2) 等底三角形面积比，等于它们的高之比； (3) 相似三角形面积比，等于它们相似比的平方．ABCDHEFG能力训练1．如图，正方形ABCD 的边长为4cm ，E 是AD 的中点，BM ⊥EC ，垂足为M ，则BM ＝______.（福建省中考试题）2．如图，矩形ABCD 中，P 为AB 上一点，AP ＝ 2BP ，CE ⊥DP 于E ，AD ＝a ，AB ＝b ，则CE ＝__________.（南宁市中考试题）MEADBCEDACBP1214814425CBAHGF DEQ TPR第1题图 第2题图 第3题图3．如图，已知八边形ABCDEFGH 中四个正方形的面积分别为25，48，121，114，PR ＝13，则该八边形的面积为____________.（江苏省竞赛试题）4. 在△ABC 中，三边长为3=a ，4=b ，6=c ，a h 表示a 边上的高的长，b h ，c h 的意义类似，则(a h ＋b h ＋c h )⋅⎪⎪⎭⎫⎝⎛++c b ah h h 111的值为____________. （上海市竞赛试题）5．如图，△ABC 的边AB ＝2，AC ＝3，Ⅰ，Ⅱ，Ⅲ分别表示以AB ，BC ，CA 为边的正方形，则图中三个阴影部分的面积之和的最大值是__________.（全国竞赛试题）6．如图，过等边△ABC 内一点P 向三边作垂线，PQ ＝6，PR ＝8，PS ＝10，则△ABC 的面积是 ( )．A. 3192B. 3190C. 3194D.3196（湖北省黄冈市竞赛试题）ⅢⅠⅡEBADCRSQAPCBDBCA第5题图 第6题图 第7题图 7．如图，点D 是△ABC 的边BC 上一点，若∠CAD ＝∠DAB ＝060，AC ＝3，AB ＝6，则AD 的长是( )．A ．2 B. 212 C.3 D. 2138．如图，在四边形ABCD 中，M ，N 分别是AB ，CD 的中点，AN ，BN ，DM ，CM 划分四边形所成的7个区域的面积分别为1S ，2S ，3S ，4S ，5S ，6S ，7S ，那么恒成立的关系式是( )．A. 2S +6S =4SB.1S +7S =4SC. 2S +3S =4S D ．1S +6S =4SS 1S 2S 6S 7S 5S 3S 4NMAB DC9．已知等边△ABC 和点P ，设点P 到△ABC 三边AB ，AC ，BC 的距离分别为1h ，2h ，3h ，△ABC 的高为h ．若点P 在一边BC 上（如图1），此时03 h ，可得结论：1h ＋2h ＋3h ＝h . 请直接用上述信息解决下列问题：当点P 在△ABC 内（如图2）、点P 在△ABC 外（如图3）这两种情况时，上述结论是否还成立？若成立．请给予证明；若不成立，1h ，2h ，3h 与h 之间又有怎样的关系？请写出你的猜想，不需证明．（黑龙江省中考试题）图3图2图1MM M F E DAF E DA EDA BCPBC P BCP10.如图，已知D ，E ，F 分别是锐角△ABC 的三边BC ，CA ，AB 上的点，且AD 、BE 、CF 相交于P 点，AP ＝BP ＝CP ＝6，设PD ＝x ，PE ＝y ，PF ＝z ，若28=++zx yz xy ，求xyz 的值．（“希望杯”邀请赛试题）EPDACBF11.如图，在凸五边形ABCDE 中，已知AB ∥CE，BC ∥AD ，BE ∥CD ，DE ∥AC ，求证：AE ∥BD .（加拿大数学奥林匹克试题）DABC ER P Q E DC B A F 12.如图，在锐角△ABC 中，D ，E ，F 分别是AB ，BC ，CA 边上的三等分点. P ，Q ，R 分别是△ADF ，△BDE ，△CEF 的三条中线的交点.(1) 求△DEF 与△ABC 的面积比；(2) 求△PDF 与△ADF 的面积比；(3) 求多边形PDQERF 与△ABC 的面积比.13．如图，依次延长四边形ABCD 的边AB ，BC ，CD ，DA 至E ，F ，G ，H ，使m DAAHCD DG BC CF AB BE ====， 若ABCD EFGH S S 四边形四边形2=，求m 的值． （上海市竞赛试题）HEFGAD CB14. 如图，一直线截△ABC 的边AB ，AC 及BC 的延长线分别交于F ，E ，D 三点，求证：1=⋅⋅FBAFEA CE DC BD ． （梅涅劳斯定理）EBDA CF15．如图，在△ABC 中，已知21===FA FB EC EA DB DC ，求ABC GHI S S ∆∆的值.（“华罗庚金杯”少年数学邀请赛试题）。

初中数学几何模型（九）面积模型1、铅锤法模型：如图，过△ABC的顶点C、B作铅垂线，顶点A作水平线。

线段a叫△ABC的“水平宽”，线段b叫△ABC的“铅锤高度”。

这样我们可以得到求三角形面积的一种方法：S△ABC=12ab，即三角形面积等于水平宽度与铅锤高度乘积的一半。

在平面直角坐标系中，二次函数、反比例函数为基架的动态问题中，确定水平宽度和铅锤高度，并使用铅锤法求斜三角形的面积及相关最值问题。

口诀：“歪歪三角形中间砍一刀”。

典型例题：1、如图，在平面直角坐标系中，已知A（1，1）、B（7，3）、C（4，7），求△ABC的面积。

略解：∵A（1，1）、B（7，3），∴水平宽度AE=6；可以根据中点坐标公式、可以用三角形中位线定理、也可以用待定系数法求出直线AB的解析式三种思路求出点D（4，2），∴铅锤高度CD=5；根据铅锤法求S△ABC=12ab=12×AE×CD=12×6×5=15（平方单位）。

2、如图，抛物线y=x2-2x-3与x轴交于A、B两点，与y轴交于点C，抛物线的顶点为G。

（1）求△ABC和△BCG的面积；（2）若点D在直线BC下方抛物线上运动，求△BCD面积的最大值。

（3）若点D在直线BC下方抛物线上运动，求四边形ACDB面积的最大值。

2、等积模型：用不同方法表示同一个图形的面积，结果相等。

（1）当所表示的图形是“规则”图形时，不同的方法指的是：①直接用面积公式表示；②用其他图形面积的和或差表示。

（2）当所表示的图形是“不规则”的图形时，不同方法指的是：用割补法来表示。

典型例题：1、在Rt△ABC中，∠C=90°，CD是斜边上的高，用直角三角形的三边表示斜边上的高CD。

解：∵S △ABC =12ch ，S △ABC =12ab ，∴12ch =12ab ，∴h=ab c。

结论：直角三角形斜边上的高等于两直角边的乘积除以斜边。

2、（1）如图①，已知△ABC 中，AB=AC ，点P 是BC 上的一点，PN ⊥AC 于点N ，PM ⊥AB 于点M ，CG ⊥AB 于点G ，求证：CG=PM+PN 。

初中数学几何面积求法大全！
几何”问题不仅是初中数学的重点，到了高中数学学习中也占很大比重，内容是循序渐进的，所以基础一定要打好。

在初中数学几何考试中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算，一般我们称这样的图形为不规则图形。

对于这类不规则图形，考试常考的就是求图形中的阴影面积。

一、公式法
这属于最简单的方法，阴影面积是一个常规的几何图形，例如三角形、正方形等等。

简单举出2个例子：
二、和差法
攻略一：直接和差法
这类题目也比较简单，属于一目了然的题目。

只需学生用两个或多个常见的几何图形面积进行加减。

攻略二：构造和差法
从这里开始，学生就要构建自己的数学图形转化思维了，学会通过添加辅助线进行求解。

三、割补法
割补法，是学生拥有比较强的转化能力后才能轻松运用的，否则学生看到这样的题目还是会无从下手。

尤其适用于直接求面积较复杂或无法计算时，通过对图形的平移、旋转、割补等，为利用公式法或和差法求解创造条件。

攻略一：全等法
攻略二：对称法
攻略三：平移法
攻略四：旋转法
版权声明：我们尊重版权，转载已注明来源，如反对转载，请联系删除。

详情请点击版权声明和原创声明。