面积计算(例4)
- 格式:ppt
- 大小:1.80 MB
- 文档页数:9

面积的计算方法面积是描述一个平面图形所占据的空间大小的概念,我们在日常生活中经常会遇到需要计算面积的情况,比如房屋的装修、土地的规划、园艺设计等。
因此,了解面积的计算方法是非常重要的。
本文将为大家介绍常见图形的面积计算方法,希望能够帮助大家更好地理解和运用面积的概念。
1. 矩形的面积计算方法。
矩形是最简单的图形之一,其面积计算方法也非常简单。
矩形的面积等于其长和宽的乘积,即面积=长×宽。
例如,一个长为5米,宽为3米的矩形的面积为5×3=15平方米。
2. 正方形的面积计算方法。
正方形是一种特殊的矩形,其四条边长度相等。
因此,正方形的面积计算方法与矩形相同,即面积=边长×边长。
例如,一个边长为4米的正方形的面积为4×4=16平方米。
3. 三角形的面积计算方法。
三角形是另一种常见的图形,其面积计算方法与矩形和正方形略有不同。
三角形的面积等于底边长度与高的乘积再除以2,即面积=(底边长度×高)÷2。
例如,一个底边长为6米,高为4米的三角形的面积为(6×4)÷2=12平方米。
4. 圆的面积计算方法。
圆是一个没有边界的闭合曲线,其面积计算方法与其他图形有所不同。
圆的面积等于π乘以半径的平方,即面积=πr²,其中π的近似值为3.14,r为圆的半径。
例如,一个半径为5米的圆的面积为3.14×5²=78.5平方米。
5. 梯形的面积计算方法。
梯形是一个有两个平行边的四边形,其面积计算方法较为复杂。
梯形的面积等于上底和下底长度之和乘以高再除以2,即面积=(上底长+下底长)×高÷2。
例如,一个上底长为3米,下底长为5米,高为4米的梯形的面积为(3+5)×4÷2=16平方米。
总结。
通过以上介绍,我们可以看出不同图形的面积计算方法各有不同,但都遵循着一定的规律。
掌握这些计算方法,可以帮助我们更好地理解和运用面积的概念,为实际生活中的问题提供解决方案。



割补法求面积经典例题当涉及到计算面积的经典例题时,割补法是一种常用且有效的方法。
下面割补法求面积的经典例题:1. 一个矩形的长为10cm,宽为5cm,求其面积。
解:面积= 长×宽= 10cm ×5cm = 50cm²2. 一个正方形的边长为7cm,求其面积。
解:面积= 边长×边长= 7cm ×7cm = 49cm²3. 一个圆的半径为3cm,求其面积(取π=3.14)。
解:面积= π×半径²= 3.14 ×3cm ×3cm = 28.26cm²4. 一个梯形的上底长为6cm,下底长为8cm,高为4cm,求其面积。
解:面积= (上底长+ 下底长)×高÷2 = (6cm + 8cm)×4cm ÷2 = 28cm²5. 一个三角形的底边长为9cm,高为12cm,求其面积。
解:面积= 底边长×高÷2 = 9cm ×12cm ÷2 = 54cm²6. 一个平行四边形的底边长为10cm,高为6cm,求其面积。
解:面积= 底边长×高= 10cm ×6cm = 60cm²7. 一个等边三角形的边长为5cm,求其面积。
解:面积= (边长²×√3)÷4 = (5cm ×5cm ×√3)÷4 ≈10.83cm ²8. 一个正五边形的边长为8cm,求其面积。
解:面积= (5 ×边长²×√5)÷4 = (5 ×8cm ×8cm ×√5)÷4 ≈110.85cm²9. 一个正六边形的边长为12cm,求其面积。
解:面积= (6 ×边长²×√3)÷4 = (6 ×12cm ×12cm ×√3)÷4 ≈374.12cm²10. 一个扇形的半径为5cm,圆心角为60°,求其面积(取π=3.14)。

第十四讲面积的计算长方形和正方形的面积公式:长方形面积=长×宽。
正方形面积=边长X边长。
对于一些不规则的图形面积,我们不能生搬硬套地使用公式。
应该通过合理的分割、添补、移位、分解、转化等方法,将它们转化成标准的图形来算面积。
【例1】l小明把右图划分成两个长方形,求面积(见图1、图2)小红采用长方形面积减去正方形的面积的方法算(见图3),你还能用其他的方法计算右图白面积吗? (单位:厘米)【例2】有一个长方形菜园,如果把宽改成50米,长不变,那么它面积减少680平方米,如果使宽为60米,长不变,那么它面积比原来增加2720平方米,原来的长和宽各是多少米? 思路点拨:根据题意,可以用下图表示增减变化的情况【例3】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?例4一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形。
求第五个正方形的面积。
同步练习四求下图阴影部分的面积。
【例5】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差多少? (单位:厘米)同步练习五1、下图中,大正方形的边长是7厘米,小正方形的边长是4厘米。
这两个正方形有一部分重合,那么两块没有重合的阴影部分A和B的面积相差是多少?【巩固练习】1.人民路小学操场原来长80米,宽55米,改造后长增加20米,宽减少5米,现在操场的面积比原来增加多少?2.一块长方形地长是80米,宽是45米。
如果把宽增加5米,要使原来的面积不变,长应减少多少米?3.有一块长方形木板,长24分米,宽4分米。
如果长和宽分别减少10分米、2分米、面积就比原来减少多少平方分米?4.一块长50米、宽30米的草坪,修建以后,草坪的面积比原来大600平方米,己知修建以后,长是60米,修建后的宽增加了多少米?5.右图是某养禽专业户用一段长18米的篱笆围成一个长方形的养鸡场,求养鸡场占地面积是多大?6、图中大正方形的边长是15分米,小正方形的边长比大正万形的边长少2分米。
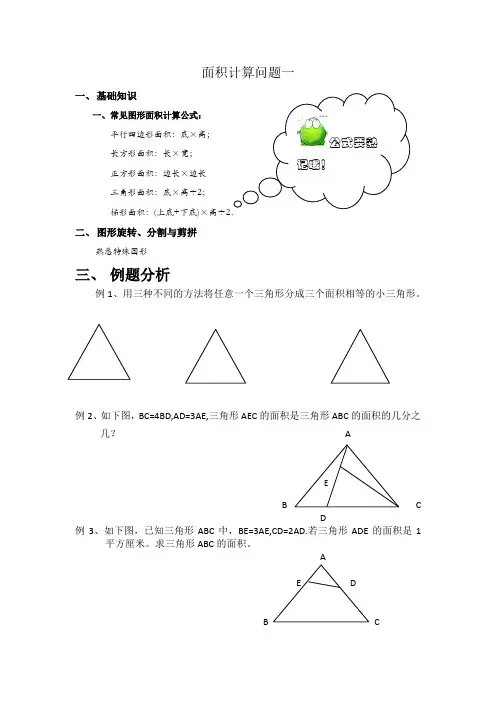
面积计算问题一一、 基础知识一、常见图形面积计算公式:平行四边形面积:底×高;长方形面积:长×宽;正方形面积:边长×边长三角形面积:底×高÷2;梯形面积:(上底+下底)×高÷2二、 图形旋转、分割与剪拼熟悉特殊图形三、例题分析例1、用三种不同的方法将任意一个三角形分成三个面积相等的小三角形。
例2、如下图,BC=4BD,AD=3AE,三角形AEC 的面积是三角形ABC 的面积的几分之几? AB C D例3、如下图,已知三角形ABC 中,BE=3AE,CD=2AD.若三角形ADE 的面积是1平方厘米。
求三角形ABC 的面积。
B C公式要熟记哦!例4、如下图,将三角形ACB 的边BA 、AC 、CB 分别延长一倍到D 、E 、F 。
已知三角形ABC 的面积为2平方厘米,求三角形DEF 的面积。
DAC B E F例5、如下图,三角形ABC ,BD=2AD ,AG=CG ,BE=EF=FC ,三角形ABC 的面积为18平方厘米,求DEFG 的面积。
A DGB C E F例6、如图是由两个完全一样的直角三角形叠在一起而成的,求DFCG 部分的面积 (单位:里米)。
DA38 FGB 5 E C例7、三角形ABC 的面积为10平方厘米,AE=21AD,BD=3DC,求三角形BDE 的面积。
AE FB D C课后练习1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形。
2、如下图,三角形ABC的面积为27平方厘米,E、F分别是AC、BC的三等分点,求三角形BEF的面积。
CFEA B3、如下图,D、E、F分别是BC、AD、BE的三等分点,三角形ABC的面积是27平方厘米,求三角形DEF的面积是多少?BDFEA4、如图,将三角形ABC的边BA、AC、CB分别延长1倍、2倍、3倍到D、E、F。
已知三角形ABC的面积为1.求三角形DEF的面积DAC BEF5、AE=ED,BD=2DC , =40平方厘米。

长方形和正方形的面积计算听课记录
摘要:
1.长方形和正方形的面积公式介绍
2.长方形和正方形面积计算实例
3.面积计算在实际生活中的应用
4.总结与拓展
正文:
一、长方形和正方形的面积公式介绍
长方形的面积公式为:面积= 长× 宽;正方形的面积公式为:面积= 边长× 边长。
这两个公式是几何学中最基础的面积计算方法,掌握它们对于学习几何学具有重要意义。
二、长方形和正方形面积计算实例
1.长方形的面积计算:假设一个长方形的长为5厘米,宽为3厘米,根据公式面积= 长× 宽,可得该长方形的面积为:5 × 3 = 15(平方厘米)。
2.正方形的面积计算:假设一个正方形的边长为4厘米,根据公式面积= 边长× 边长,可得该正方形的面积为:4 × 4 = 16(平方厘米)。
三、面积计算在实际生活中的应用
1.家居装修:在家庭装修中,需要测量房间的长和宽,根据长方形面积公式计算出房间面积,进而确定地板、墙纸等材料的用量。
2.土地测量:在农村土地划分或城市房地产开发中,需要测量土地的长和宽,根据长方形面积公式计算出土地面积,以便进行合理规划。
3.建筑施工:在建筑施工过程中,工程师需要根据设计图纸上的长方形或正方形结构,计算出各种建筑材料的用量,以确保施工进度和质量。
四、总结与拓展
掌握长方形和正方形的面积计算方法,不仅可以解决几何题,还能够应用于实际生活中。
此外,还可以进一步学习其他图形的面积计算方法,如圆、三角形、梯形等,从而丰富自己的几何知识。

面积计算题型大全(有答案)1. 长方形面积计算题目:一块长方形田地的长为12米,宽为8米,求其面积。
答案:面积 = 长 ×宽 = 12米 × 8米 = 96平方米2. 正方形面积计算题目:一块正方形花坛的边长为5米,求其面积。
答案:面积 = 边长 ×边长 = 5米 × 5米 = 25平方米3. 圆形面积计算题目:一个半径为6米的圆的面积是多少?答案:面积= π × 半径 ×半径 = 3.14 × 6米 × 6米≈ 113.04平方米4. 梯形面积计算题目:一个梯形的上底长为8米,下底长为12米,高为5米,求其面积。
答案:面积 = (上底长 + 下底长)×高 ÷ 2 = (8米 + 12米)×5米 ÷ 2 = 50平方米5. 三角形面积计算题目:一个三角形的底边长为10米,高为6米,求其面积。
答案:面积 = 底边长 ×高 ÷ 2 = 10米 × 6米 ÷ 2 = 30平方米6. 棱柱面积计算题目:一个棱柱的底面积为12平方米,高为8米,求其面积。
答案:面积 = 底面积 + 侧面积 = 12平方米 + (周长 ×高) = 12平方米 + (底周长 ×高) = 12平方米 + ((边1 + 边2 + 边3 + 边4)×高) = 12平方米 + ((a + b + c + d)×高)7. 球体表面积计算题目:一个半径为4米的球的表面积是多少?答案:表面积= 4π × 半径 ×半径= 4π × 4米 × 4米≈ 201.06平方米以上是一些常见的面积计算题型及其答案,希望对您有帮助!。

面积计算公式长方形的周长=(长+宽)×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=(上底+下底)×高÷2直径=半径×2半径=直径÷2圆的周长=圆周率×直径= 圆周率×半径×2 圆的面积=圆周率×半径×半径长方体的表面积= (长×宽+长×高+宽×高)×2 长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体(正方体、圆柱体) 的体积=底面积×高平面图形名称符号周长C和面积S 正方形a-边长C=4a S=a2长方形a和b-边长C=2(a+b)S=ab 三角形a,b,c-三边长h-a边上的高s-周长的一半A,B,C-内角其中s=(a+b+c)/2 S=ah/2 =ab/2·sinC=[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)四边形d,D-对角线长α-对角线夹角S=dD/2·sinα平行四边形a,b-边长h-a边的高α-两边夹角S=ah=absinα菱形a-边长α-夹角D-长对角线长d-短对角线长S=Dd/2 =a2sinα梯形a和b-上、下底长h-高m-中位线长S=(a+b)h/2 =mh圆r-半径d-直径C=πd=2πrS=πr2 =πd2/4扇形r-扇形半径a-圆心角度数C=2r+2πr×(a/360)S=πr2×(a/360)弓形l-弧长b-弦长h-矢高r-半径α-圆心角的度数S=r2/2·(πα/180-sinα) =r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2 =παr2/360 - b/2·[r2-(b/2)2]1/2 =r(l-b)/2 + bh/2 ≈2bh/3圆环R-外圆半径r-内圆半径D-外圆直径d-内圆直径S=π(R2-r2) =π(D2-d2)/4椭圆D-长轴d-短轴S=πDd/4立方图形名称符号面积S和体积V正方体a-边长S=6a2V=a3长方体a-长b-宽c-高S=2(ab+ac+bc)V=abc棱柱S-底面积h-高V=Sh棱锥S-底面积h-高V=Sh/3棱台S1和S2-上、下底面积h-高V=h[S1+S2+(S1S1)1/2]/3拟柱体S1-上底面积S2-下底面积S0-中截面积h-高V=h(S1+S2+4S0)/6圆柱r-底半径h-高C-底面周长S底-底面积S侧-侧面积S表-表面积C=2πr S底=πr2 S侧=Ch S表=Ch+2S底V=S底h =πr2h空心圆柱R-外圆半径r-内圆半径h-高V=πh(R2-r2)直圆锥r-底半径h-高V=πr2h/3 圆台r-上底半径R-下底半径h-高V=πh(R2+Rr+r2)/3球r-半径d-直径V=4/3πr3=πd2/6球缺h-球缺高r-球半径a-球缺底半径V=πh(3a2+h2)/6 =πh2(3r-h)/3 a2=h(2r-h)球台r1和r2-球台上、下底半径h-高V=πh[3(r12+r22)+h2]/6圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr2 =π2Dd2/4桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D2+d2)/12 (母线是圆弧形,圆心是桶的中心) V=πh(2D2+Dd+3d2/4)/15 (母线是抛物线形)。

公式: 长方形面积=长x 宽 相反 长=面积÷宽 (宽=面积÷长)
长方形周长=(长+宽) ×2 相反 长=周长÷2-宽(宽=周长÷2-长) 正方形面积=边长×边长 相反 边长=面积÷边长
正方形周长=边长×4 相反 边长=周长÷4
一、计算下面图形的周长和面积。
二、计算下列各题。
1.已知长方形的长为19米,宽为10米,求它的面积和周长。
2.已知面积为63平方厘米的长方形,它的长为9厘米,求它的宽和周长。
3.已知长方形的周长为50米,长为20米,求它的面积。
4.有一个边长为24分米的正方形,它的面积是多大?周长是多大?
5.已知一个正方形的周长是64米,问它的面积是多大?
6.在某个公园中,有一个长为8米,宽6米长方形的花园,员工们要在花园中种上花草,它的种植面积有多大?如果每种1平方米的花草就要花费52元,铺完整个花园要用多少元?
7.小明家有个长6米,宽3米长方形的养猪栏,现在他爸爸要重新加固,要在长方形猪栏四周绕上一圈铁线。
(1)假如小明爸爸买了15米长的铁线够用吗?如果不够用小明爸爸至少要买多长的铁线?
(2)要是每2平方米就能够养下一头猪,那小明家的养猪栏能养多少头猪?
8.在小红家里有个正方形的水池,已知它的边长是4米,那它的面积有多大?小红要是沿着水池行走了三圈,她行走了多少米?。

图形面积计算系列题(四)不规则图形面积的计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形,它们的面积及周长都有相应的公式直接计算。
实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。
一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例1 如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米。
求阴影部分的面积。
BC D解:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG 、△BDE 、△EFG )的面积之和。
因为S △ABG =21×10×10=50; S △BDE =21(10+12)×12=132;S △EFG =21(12-10)×12=12。
又因为S 甲+S 乙=12×12+10×10=244,所以阴影部分面积=244-(50+132+12)=50(平方厘米) 例2 如下图,正方形ABCD 的边长为6厘米,△ABE 、 △ADF 与四边形AECF 的面积彼此相等,求三角形AEF 的面积。
解:因为△ABE 、△ADF 与四边形AECF 的面积彼此相等,所以四边形AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 面积的三分之一。
也就是: S 四边形AECF =S △ABE =S △ADF =31×6×6=12。
在△ABE 中,因为AB=6,所以BE=4,同理DF=4,因此,CE=CF=2,所以△ECF 的面积为2×2÷2=2。
所以S △AEF = S 四边形AECF -S △ECF =12-2=10(平方厘米)。
简单的面积计算是小学数学的一项重要内容.要会计算面积,首先要能识别一些特别的图形:正方形、三角形、平行四边形、梯形等等,然后会计算这些图形的面积.如果我们把这些图形画在方格纸上,不但容易识别,而且容易计算.上面左图是边长为 4的正方形,它的面积是 4×4= 16(格);右图是 3×5的长方形,它的面积是 3×5= 15(格).上面左图是一个锐角三角形,它的底是5,高是4,面积是 5×4÷2= 10(格);右图是一个钝角三角形,底是4,高也是4,它的面积是4×4÷2=8(格).这里特别说明,这两个三角形的高线一样长,钝角三角形的高线有可能在三角形的外面.上面左图是一个平行四边形,底是5,高是3,它的面积是 5× 3= 15(格);右图是一个梯形,上底是 4,下底是7,高是4,它的面积是(4+7)×4÷2=22(格).上面面积计算的单位用“格”,一格就是一个小正方形.如果小正方形边长是1厘米,1格就是1平方厘米;如果小正方形边长是1米,1格就是1平方米.也就是说我们设定一个方格的边长是1个长度单位,1格就是一个面积单位.在这一讲中,我们直接用数表示长度或面积,省略了相应的长度单位和面积单位.一、三角形的面积用直线组成的图形,都可以划分成若干个三角形来计算面积.三角形面积的计算公式是:三角形面积= 底×高÷2.这个公式是许多面积计算的基础.因此我们不仅要掌握这一公式,而且要会灵活运用.例1 右图中BD长是4,DC长是2,那么三角形ABD的面积是三角形ADC面积的多少倍呢?解:三角形ABD与三角形ADC的高相同.三角形ABD面积=4×高÷2.三角形 ADC面积=2×高÷2.因此三角形ABD的面积是三角形ADC面积的2倍.注意:三角形的任意一边都可以看作是底,这条边上的高就是三角形的高,所以每个三角形都可看成有三个底,和相应的三条高.例2右图中,BD,DE,EC的长分别是2,4,2.F是线段AE的中点,三角形ABC的高为4.求三角形DFE的面积.解: BC= 2+ 4+ 2= 8.三角形 ABC面积= 8× 4÷2=16.我们把A和D连成线段,组成三角形ADE,它与三角形ABC的高相同,而DE长是4,也是BC的一半,因此三角形ADE面积是三角形ABC面积的一半.同样道理,EF是AE的一半,三角形DFE面积是三角形ADE面积的一半.三角形 DFE面积= 16÷4=4.例3右图中长方形的长是20,宽是12,求它的内部阴影部分面积.解:ABEF也是一个长方形,它内部的三个三角形阴影部分高都与BE一样长.而三个三角形底边的长加起来,就是FE的长.因此这三个三角形的面积之和是FE×BE÷2,它恰好是长方形ABEF面积的一半.同样道理,FECD也是长方形,它内部三个三角形(阴影部分)面积之和是它的面积的一半.因此所有阴影的面积是长方形ABCD面积的一半,也就是20×12÷2=120.通过方格纸,我们还可以从另一个途径来求解.当我们画出中间两个三角形的高线,把每个三角形分成两个直角三角形后,图中每个直角三角形都是某个长方形的一半,而长方形ABCD是由这若干个长方形拼成.因此所有这些直角三角形(阴影部分)的面积之和是长方形ABCD面积的的一半.例4 右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?解:把A和C连成线段,四边形ABCD就分成了两个,三角形ABC和三角形ADC.对三角形ABC来说,AB是底边,高是10,因此面积=4×10÷2= 20.对三角形 ADC来说, DC是底边,高是 8,因此面积=7×8÷2=28.四边形 ABCD面积= 20+ 28= 48.这一例题再一次告诉我们,钝角三角形的高线有可能是在三角形的外面.例5在边长为6的正方形内有一个三角形BEF,线段AE=3,DF=2,求三角形BEF的面积.解:要直接求出三角形BEF的面积是困难的,但容易求出下面列的三个直角三角形的面积三角形 ABE面积=3×6×2= 9.三角形 BCF面积= 6×(6-2)÷2= 12.三角形 DEF面积=2×(6-3)÷2= 3.我们只要用正方形面积减去这三个直角三角形的面积就能算出:三角形 BEF面积=6×6-9-12-3=12.例6 在右图中,ABCD是长方形,三条线段的长度如图所示,M是线段DE的中点,求四边形ABMD(阴影部分)的面积.解:四边形ABMD中,已知的太少,直接求它面积是不可能的,我们设法求出三角形D CE与三角形MBE的面积,然后用长方形ABCD的面积减去它们,由此就可以求得四边形AB MD的面积.把M与C用线段连起来,将三角形DCE分成两个三角形.三角形 DCE的面积是 7×2÷2=7.因为M是线段DE的中点,三角形DMC与三角形MCE面积相等,所以三角形MCE面积是 7÷2=3.5.因为 BE= 8是 CE= 2的 4倍,三角形 MBE与三角形MCE高一样,因此三角形MBE 面积是3.5×4=14.长方形 ABCD面积=7×(8+2)=70.四边形 ABMD面积=70-7- 14= 49.二、有关正方形的问题先从等腰直角三角形讲起.一个直角三角形,它的两条直角边一样长,这样的直角三角形,就叫做等腰直角三角形.它有一个直角(90度),还有两个角都是45度,通常在一副三角尺中.有一个就是等腰直角三角形.两个一样的等腰直角三角形,可以拼成一个正方形,如图(a).四个一样的等腰直角三角形,也可以拼成一个正方形,如图(b).一个等腰直角三角形,当知道它的直角边长,从图(a)知,它的面积是直角边长的平方÷2.当知道它的斜边长,从图(b)知,它的面积是斜边的平方÷4例7 右图由六个等腰直角三角形组成.第一个三角形两条直角边长是8.后一个三角形的直角边长,恰好是前一个斜边长的一半,求这个图形的面积.解:从前面的图形上可以知道,前一个等腰直角三角形的两个拼成的正方形,等于后一个等腰直角三角形四个拼成的正方形.因此后一个三角形面积是前一个三角形面积的一半,第一个等腰直角三角形的面积是8×8÷2=32.这一个图形的面积是32+16+ 8+ 4 + 2+1= 63.例8 如右图,两个长方形叠放在一起,小长形的宽是2,A点是大长方形一边的中点,并且三角形ABC是等腰直角三角形,那么图中阴影部分的总面积是多少?解:为了说明的方便,在图上标上英文字母 D,E,F,G.三角形ABC的面积=2×2÷2=2.三角形ABC,ADE,EFG都是等腰直角三角形.三角形ABC的斜边,与三角形ADE的直角边一样长,因此三角形 ADE面积=AB C面积×2=4.三角形EFG的斜边与三角形ABC的直角边一样长.因此三角形EFG面积=ABC面积÷2=1.阴影部分的总面积是 4+1=5.例9如右图,已知一个四边形ABCD的两条边的长度AD=7,BC=3,三个角的度数:角 B和D是直角,角A是45°.求这个四边形的面积.解:这个图形可以看作是一个等腰直角三角形ADE,切掉一个等腰直角三角形BCE.因为A是45°,角D是90°,角E是180°-45°-90°= 45°,所以ADE是等腰直角三角形,BCE也是等腰直角三角形.四边形ABCD的面积,是这两个等腰直角三角形面积之差,即7×7÷2-3×3÷2=20.这是1994小学数学奥林匹克决赛试题.原来试题图上并没有画出虚线三角形.参赛同学是不大容易想到把图形补全成为等腰直角三角形.因此做对这道题的人数不多.但是有一些同学,用直线AC把图形分成两个直角三角形,并认为这两个直角三角形是一样的,这就大错特错了.这样做,角 A是 45°,这一条件还用得上吗?图形上线段相等,两个三角形相等,是不能靠眼睛来测定的,必须从几何学上找出根据,小学同学尚未学过几何,千万不要随便对图形下结论.我们应该从题目中已有的条件作为思考的线索.有45°和直角,你应首先考虑等腰直角三角形.现在我们转向正方形的问题.例10 在右图 11×15的长方形内,有四对正方形(标号相同的两个正方形为一对),每一对是相同的正方形,那么中间这个小正方形(阴影部分)面积是多少?解:长方形的宽,是“一”与“二”两个正方形的边长之和,长方形的长,是“一”、“三”与“二”三个正方形的边长之和.长-宽 =15-11=4是“三”正方形的边长.宽又是两个“三”正方形与中间小正方形的边长之和,因此中间小正方形边长=11-4×2=3.中间小正方形面积=3×3= 9.如果把这一图形,画在方格纸上,就一目了然了.例11从一块正方形土地中,划出一块宽为1米的长方形土地(见图),剩下的长方形土地面积是15.75平方米.求划出的长方形土地的面积.解:剩下的长方形土地,我们已知道长-宽=1(米).还知道它的面积是15.75平方米,那么能否从这一面积求出长与宽之和呢?如果能求出,那么与上面“差”的算式就形成和差问题了.我们把长和宽拼在一起,如右图.从这个图形还不能算出长与宽之和,但是再拼上同样的两个正方形,如下图就拼成一个大正方形,这个正方形的边长,恰好是长方形的长与宽之和.可是这个大正方形的中间还有一个空洞.它也是一个正方形,仔细观察一下,就会发现,它的边长,恰好是长方形的长与宽之差,等于1米.现在,我们就可以算出大正方形面积:15.75×4+1×1= 64(平方米).64是8×8,大正方形边长是 8米,也就是说长方形的长+宽=8(米).因此长=(8+1)÷2= 4.5(米).宽=8-4.5=3.5(米).那么划出的长方形面积是4.5×1=4. 5(平方米).例12 如右图.正方形ABCD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6,求三角形AEG(阴影部分)的面积.解:四边形AECD是一个梯形.它的下底是AD,上底是EC,高是CD,因此四边形AECD面积=(小正方形边长+大正方形边长)×大正方形边长÷2三角形ADG是直角三角形,它的一条直角边长DG=(小正方形边长+大正方形边长),因此三角形ADG面积=(小正方形边长+大正方形边长)×大正方形边长÷2.四边形 AECD与三角形 ADG面积一样大.四边形AHCD是它们两者共有,因此,三角形AEH与三角形HCG面积相等,都加上三角形EHG面积后,就有阴影部分面积=三角形ECG面积=小正方形面积的一半= 6×6÷2=18.十分有趣的是,影阴部分面积,只与小正方形边长有关,而与大正方形边长却没有关系.三、其他的面积这一节将着重介绍求面积的常用思路和技巧.有些例题看起来不难,但可以给你启发的内容不少,请读者仔细体会.例13 画在方格纸上的一个用粗线围成的图形(如右图),求它的面积.解:直接计算粗线围成的面积是困难的,我们通过扣除周围正方形和直角三角形来计算.周围小正方形有3个,面积为1的三角形有5个,面积为1.5的三角形有1个,因此围成面积是4×4-3-5-1.5=6.5.例6与本题在解题思路上是完全类同的.例14 下图中 ABCD是 6×8的长方形,AF长是4,求阴影部分三角形AEF的面积.解:三角形AEF中,我们知道一边AF,但是不知道它的高多长,直接求它的面积是困难的.如果把它扩大到三角形AEB,底边AB,就是长方形的长,高是长方形的宽,即BC的长,面积就可以求出.三角形AEB的面积是长方形面积的一半,而扩大的三角形AFB是直角三角形,它的两条直角边的长是知道的,很容易算出它的面积.因此三角形AEF面积=(三角形 AEB面积)-(三角形 AFB面积)=8×6÷2-4×8÷2= 8.这一例题告诉我们,有时我们把难求的图形扩大成易求的图形,当然扩大的部分也要容易求出,从而间接地解决了问题.前面例9的解法,也是这种思路.例15 下左图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)有多大?解:我们首先要弄清楚,平行四边形面积有多大.平行四边形的面积是底×高.从图上可以看出,底是2,高恰好是长方形的宽度.因此这个平行四边形的面积与 10×2的长方形面积相等.可以设想,把这个平行四边形换成 10×2的长方形,再把横竖两条都移至边上(如前页右图),草地部分面积(阴影部分)还是与原来一样大小,因此草地面积=(16-2)×(10-2)= 112.例16 右图是两个相同的直角三角形叠在一起,求阴影部分的面积.解:实际上,阴影部分是一个梯形,可是它的上底、下底和高都不知道,不能直接来求它的面积.阴影部分与三角形BCE合在一起,就是原直角三角形.你是否看出,ABCD也是梯形,它和三角形BCE合在一起,也是原直角三角形.因此,梯形ABCD的面积与阴影部分面积一样大.梯形ABCD的上底BC,是直角边AD 的长减去3,高就是DC的长.因此阴影部分面积等于梯形 ABCD面积=(8+8-3)×5÷2= 32.5.上面两个例子都启发我们,如何把不容易算的面积,换成容易算的面积,数学上这叫等积变形.要想有这种“换”的本领,首先要提高对图形的观察能力.例17 下图是两个直角三角形叠放在一起形成的图形.已知 AF,FE,E C都等于3, CB, BD都等于 4.求这个图形的面积.解:两个直角三角形的面积是很容易求出的.三角形ABC面积=(3+3+3)×4÷2=18.三角形CDE面积=(4+4)× 3÷2=12.这两个直角三角形有一个重叠部分--四边形BCEG,只要减去这个重叠部分,所求图形的面积立即可以得出.因为 AF= FE= EC=3,所以 AGF, FGE, EGC是三个面积相等的三角形.因为CB=BD=4,所以CGB,BGD是两个面积相等的三角形.2×三角形DEC面积= 2×2×(三角形 GBC面积)+2×(三角形 GCE面积).三角形ABC面积= (三角形 GBC面积)+3×(三角形GCE面积).四边形BCEG面积=(三角形GBC面积)+(三角形GCE面积)=(2×12+18)÷5=8.4.所求图形面积=12+ 18- 8.4=21.6.例18 如下页左图,ABCG是4×7长方形,DEFG是 2×10长方形.求三角形 BCM与三角形 DEM面积之差.解:三角形BCM与非阴影部分合起来是梯形ABEF.三角形DEM与非阴影部分合起来是两个长方形的和.(三角形BCM面积)-(三角形DEM面积)=(梯形ABEF面积)-(两个长方形面积之和=(7+10)×(4+2)÷2-(4×7 + 2×10)=3.例19 上右图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是多少?解:所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分,因此(三角形 ABC面积)+(三角形CDE面积)+(13+49+35)=(长方形面积)+(阴影部分面积).三角形ABC,底是长方形的长,高是长方形的宽;三角形CDE,底是长方形的宽,高是长方形的长.因此,三角形ABC面积,与三角形CDE面积,都是长方形面积的一半,就有阴影部分面积=13 + 49+ 35= 97.。
四边形的面积计算四边形的面积四边形的面积计算四边形是一个具有四条边的几何形状。
在几何学中,我们经常需要计算四边形的面积,以便解决各种实际问题。
本文将介绍如何计算常见四边形(如矩形、正方形、平行四边形和梯形)的面积,并提供相应的数学公式。
1. 矩形的面积计算矩形是一种特殊的四边形,它的对边分别平行且相等。
计算矩形的面积很简单,只需要知道矩形的长度和宽度即可。
矩形的面积公式为:面积 = 长度 ×宽度例如,假设一个矩形的长度为6米,宽度为4米。
那么它的面积可以通过下面的计算得到:面积 = 6米 × 4米 = 24平方米因此,该矩形的面积为24平方米。
2. 正方形的面积计算正方形是一种特殊的矩形,它的四条边长度相等且对边平行。
计算正方形的面积与矩形类似,只需要知道正方形的边长。
正方形的面积公式为:面积 = 边长 ×边长或面积 = 边长²假设一块地是一个正方形,边长为5米。
可以用以下公式计算出其面积:面积 = 5米 × 5米 = 25平方米所以,该正方形的面积为25平方米。
3. 平行四边形的面积计算平行四边形是具有对边平行且相等的四边形。
计算平行四边形的面积需要知道它的底边长度和高度。
平行四边形的面积公式为:面积 = 底边长度 ×高度假设平行四边形的底边长度为6米,高度为3米。
通过以下计算可以得到它的面积:面积 = 6米 × 3米 = 18平方米因此,该平行四边形的面积为18平方米。
4. 梯形的面积计算梯形是具有两条平行边的四边形。
计算梯形的面积需要知道它的上底、下底和高度。
梯形的面积公式为:面积 = (上底 + 下底) ×高度 ÷ 2假设梯形的上底长为4米,下底长为8米,高度为5米。
通过以下计算可以得到它的面积:面积 = (4米 + 8米) × 5米 ÷ 2 = 12米 × 5米 ÷ 2 = 30平方米因此,该梯形的面积为30平方米。
格点求面积公式(二)格点求面积公式什么是格点求面积公式?格点求面积公式是一种用于计算任意形状的面积的数学公式。
它将一个二维平面上的点集按照一定的规则连接起来,形成一系列的格点,然后利用这些格点来计算面积。
格点求面积公式的基本思想格点求面积公式的基本思想是将一个图形划分为多个小区域,并计算每个小区域的面积,最后将所有小区域的面积相加得到整个图形的面积。
格点求面积公式的相关公式•矩形面积公式:面积 = 长× 宽例如,某个矩形的长为5,宽为3,那么它的面积等于5 × 3 = 15平方单位。
•正方形面积公式:面积 = 边长× 边长例如,某个正方形的边长为4,那么它的面积等于 4 × 4 = 16平方单位。
•圆形面积公式:面积= π × 半径× 半径例如,某个圆的半径为3,那么它的面积等于× 3 × 3 = 平方单位。
•三角形面积公式:面积 = 底边长× 高÷ 2例如,某个三角形的底边长为6,高为4,那么它的面积等于6 × 4 ÷ 2 = 12平方单位。
•梯形面积公式:面积 = (上底长 + 下底长)× 高÷ 2例如,某个梯形的上底长为3,下底长为5,高为2,那么它的面积等于(3 + 5)× 2 ÷ 2 = 8平方单位。
格点求面积公式的应用举例1.示例一:矩形假设有一个矩形,长为10,宽为6。
我们可以使用矩形面积公式计算它的面积:面积= 10 × 6 = 60平方单位因此,该矩形的面积为60平方单位。
2.示例二:圆形假设有一个圆,半径为5。
我们可以使用圆形面积公式计算它的面积:面积= × 5 × 5 = 平方单位因此,该圆的面积为平方单位。
3.示例三:三角形假设有一个三角形,底边长为8,高为6。
我们可以使用三角形面积公式计算它的面积:面积= 8 × 6 ÷ 2 = 24平方单位因此,该三角形的面积为24平方单位。
同学个性化教学设计年级:教师: 科目:
班主任:日期: 时段:
【例 1】 在梯形中阴影部分面积是150平方厘米,求梯形面积。
【巩固】如图,已知平行四边形面积是48平方厘米,求阴影部分面积。
【例 2】 如图,是两个完全相同的直角三角形叠在一起,求阴影部分的面积。
(单位:分米)
【例 3】 如图,将长为9厘米、宽为6厘米的长方形划分成四个三角形,其面积分别为1S 、2S 、3S 、
4S ,且4321S S S S +==,求4S 。
【巩固】如图,四年级ABCD是直角三角形,其中AD=12厘米,AB=8厘米,BC=15厘米,且△ADE 四边形DEBF及△CDF的面积相等,求三角形EBF的面积。
【例 4】如图,AE=5厘米,CF=2厘米,AB=6厘米,CD=4厘米,∠B=∠D=90°。
求四边形AFCE 的面积。
【巩固】如图,四边形ABCD中,AE=5厘米,AB=10厘米,FC=12厘米,∠B=∠D=90°,求四边形AFCE的面积。
【例 5】如图,求图示长方形中阴影部分的面积。
(单位:厘米)
【例 6】如图,平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边CE长8厘米。
已知阴影部分的面积比三角形FEG的面积大10平方厘米。
求CF的长。
【巩固】如图,正方形ABCD的边长是12厘米,已知DE是EC的长度的2倍。
求(1)△DEF的面积;(2)CF的长。
学生签字:__________
教研组长签字:____
_______。
一、面积计算(一)1、如图,长方形ABCD的面积为56平方厘米,E,F, H分别是AB,DC,AD的中点,G为BC边上任意一点,求阴影部分面积。
2、如图,在ΔABC中,AD=2BD,CE=2BE,已知阴影部分面积是65平方厘米,求ΔABC面积。
3、如图,ΔABC的面积是15平方厘米,将AB,BC,、CA分别延长一倍到D,E,F,连接DE,EF,FD,求ΔDEF的面积。
1、如图,在ΔABC中,D,F是BC边三等分点,E是AB的中点,ΔDEB的面积是3平方厘米。
则ΔABC 的面积是多少2、如图,已知四边形ABCD的面积是240平方厘米,E,F分别是AB,DC的中点,求阴影部分的面积。
3、如图,AB=AD,BE=2BC,CF=3CA,ΔABC的面积为1,求ΔDEF的面积。
拓展:1、如图,ΔABC的面积是45平方厘米,AE=ED,BD=23BC,求阴影部分的面积。
2、如图,四边形ABCD对角线BD被E,F两点三等分。
已知四边形AECF面积是60平方厘米,求四边形ABCD的面积。
二、面积计算(二)1、如图,大正方形ABCD边长是12厘米,求阴影部分的面积。
2、如图,三角形ABC面积为180平方厘米,AE=2ED,D,F分别为BC,AC的中点,求阴影部分的面积。
3、大正方形和小正方形如图,已知图形周长是64厘米,DG=4厘米,求阴影部分的面积。
习题:1、如图,大正方形ABCD边长是20厘米,求阴影部分的面积。
2、如图,长方形ABCD中,AB=24厘米,BC=36厘米,E是BC的中点,F,G分别是AB,CD的4等分点,H为AD上任意一点,求阴影部分的面积。
3、如图,ΔABC和ΔDEF都是等腰直角三角形,AB=8厘米,DE=6厘米,求阴影部分的面积。
拓展:1、如图,在平行四边形ABCD中,边长BC=10厘米,直角三角形直角边EC长8厘米,已知平行四边形ABCD面积比ΔBEC大10平方厘米,求平行四边形ABCD的面积。