离散数学chapter04-2014

离散数学（微课版）第4章1. 引言在离散数学的第4章中，我们将讨论图论的基本概念和应用。

图论是研究图及其在现实生活中的应用的数学分支，它在计算机科学、网络设计、运筹学等领域中具有重要的应用价值。

本章将介绍图的定义、图的表示方法、图的遍历算法等内容。

2. 图的定义图由一组节点和一组节点之间的边构成。

节点通常表示现实世界中的对象，而边则表示对象之间的关系。

图可以用于描述各种问题，如社交网络中的用户关系、城市之间的交通网络等。

2.1 有向图和无向图图可以分为有向图和无向图两种类型。

在有向图中，边具有方向，表示节点之间的单向关系。

而在无向图中，边没有方向，表示节点之间的双向关系。

2.2 顶点和边图由顶点和边组成。

顶点是图的节点，用来表示对象。

边连接两个顶点，表示两个对象之间的关系。

2.3 路径和环路径是指在图中从一个顶点到另一个顶点的连接序列。

环是一条路径，其起点和终点相同。

3. 图的表示方法在计算机中，图可以用不同的数据结构来表示。

常见的表示方法包括：3.1 邻接矩阵邻接矩阵是用二维数组表示图的连接关系。

对于无向图，邻接矩阵是对称的，而对于有向图，则不对称。

A B CA010B101C010上述邻接矩阵表示了一个无向图，其中顶点A与顶点B相连，顶点B与顶点C相连。

3.2 邻接表邻接表是用链表表示图的连接关系。

对于每个顶点，邻接表保存了与其相连的其他顶点的信息。

A ->B -> NULLB -> A ->C -> NULLC -> B -> NULL上述邻接表表示了一个无向图，顶点A与顶点B相连，顶点B与顶点A、C相连，顶点C与顶点B相连。

4. 图的遍历算法图的遍历算法是指按照一定的方式访问图中的所有节点。

常见的图的遍历算法有深度优先搜索和广度优先搜索。

4.1 深度优先搜索深度优先搜索从起点开始，尽可能深地访问尚未访问的节点，直到无法继续深入为止，然后回溯到上一个节点，继续深入其他未访问的节点。

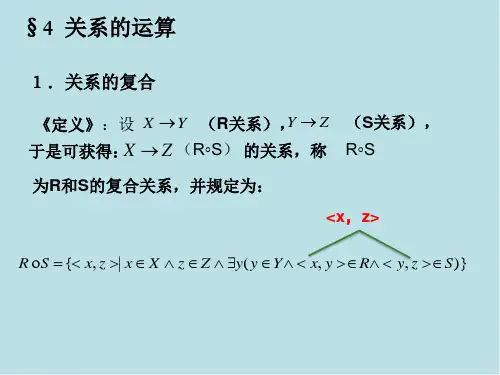
标题 Discrete Mathematical Structures Note Chapter 04主题数学笔记-笛卡尔集和商集•有序对 (a, b)•笛卡尔集- A × B = { (a, b) | a ∈ A 且 b ∈ B }-例: A = { x, y }, B = {1, 2, 3}- A × B = { (x, 1), (x, 2), (x, 3), (y, 1), (y, 2),(y, 3) }•R2 = R × RYX此图可称为笛卡尔坐标系•A1 × A2 × … × A n = {(a1, a2 …, a n) | a i ∈ A , i = 1~n}•商集( 划分 )-A, P = {A1…A k}-满⾜足(1) A1 ∪ A2 ∪ … ∪ A k=A- (2) A i ∩ A j = ∅, i≠j-称P是A的⼀一个划分•例：A = Z, A1 = {m | m ∈ A, m是偶数},A2={m | m ∈ A, m是奇数}-P = Z-A1 = {m | m ∈ Z, m < 0}-A2 = {m | m ∈ N}-P = {A1, A2}-关系•R ≤ A × B, 称R 是从A 到B 上的⼀一个关系•若A ＝B 称R 是A 上的关系•∀(a, b) ∈ A × B• (a, b) ∈ R, 记做 aRb• (a, b) ∉ R, 记做 aRb •例：A = {x, y}, B = {1, 2, 3}• R = {(x, 1)}• |A × B| = 6• |P(A ×B)| = 26• A × B 称为全关系• (x, 1) ∈ R, xR1• (x, 2) ∈ R, xR1• a | b => a 能被b 整除-关系的定义域•Dom(R) = {a | (a, b) ∈ R} Dom 称为关系的定义域•Ran(R) = {b | (a, b) ∈ R} X 的R 关系集•R(X) = {b | (x, b) ∈ R}•若R 4 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 4), (3, 3), (4, 4)}• R 4(1) = {1, 2, 3, 4}• R 4(2) = {2, 4}• R 4(3) = {3}• R 4(4) = {4}-关系的矩阵• A = {a 1, a 2, …, a m }• B = {b 1,b 2, …, b n }• A × B = {(a i , b j ) | i = 1…m, j = 1~n}•|A × B| = m × n||•|P(A ×B)| = 2m ×n 1•(a i , b j ) ∈ R•(a i , b j ) ∉ R•M R = m ×n •其中“_”的值为0或1，若M R ∈ R 则为1• A = {x, y}, B = {1, 2, 3}•R = {(x, 2), (y, 3)}•MR = -习题4.2 4〜～12（⽼老师有提）-关系的有向图•R 是A 上的关系-顶点-有向边•(a, b) ∈ R, (b, c) ∈ R• -> ->•(b, b) ∈ R•例：A = {1, 2, 3, 4}, 且 aRb <=> a|b(a 能被b 整除)-R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}•背离顶点称出数(度)•指向顶点称进数(度)_,_,…_!_,_,…_⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪0,1,00,0,1⎧⎨⎩⎫⎬⎭①②③④①②③④出度4211-关系的路径(path)•路径R 是A 上的关系•序列π ：a, x 1 …… x n-1, b•满⾜足：aRx, x 1Rx 2, …… x n-1Rb, 该π是从a 到b ⻓长度为n 的路径• A = {1, 2, 3, 4, 5}•R = {(1, 2), (2, 2), (2, 3), (2, 4), (2, 5), (4, 3), (5, 1),(5, 4)}•π1: 1, 2, 4•π2: 1, 2, 5 ,1•π3: 2, 2•π4: 1, 2, 2, 3-环：起点和终点相同的路径•恒等环：⻓长度为1的环•xRy: (x, y) ∈ R•xR 2y:从x 到y 有⼀一条⻓长度为2的路径•xR n y:从x 到y 有⼀一条⻓长度为n 的路径•xR ∞y:从x 到y 存在路径-定理：R 是A 上的关系|A|=n•则：(1) M R 2 = M R ⨀ M R• (2) M R n = M R ⨀ … ⨀M R•M R = •M R 2 = M R ⨀ M R 0 1 0 0 0 0 1 1 1 1 0 0 1 0 0 1 0 0 1 0⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟①②③⑤④•= •★此类题过程：(1) 写出R•(2) 写出M R •(3) ⽤用M R 去计算M R 2•(4) 画出R 2的有向图-复合路径(考填空)•π1: 1, 2, 5•π2: 5, 4, 3•π2o π1: 1, 2, 5, 4, 3•π1: a, x 1, … x n-1, b•π2: b, y 1, … y n-1, c•π2o π1: a, x 1, … x n-1, b, y 1, … y n-1, c-关系的性质•⾃自反性•⾃自反关系：∀ a ∈ A 有(a, a)∈R, 称R 是A 上的⾃自反关系• A = {1, 2, 3, 4}•R = {(1, 1), (2, 2), (3, 3), (4, 4)}, ⾃自少包含所有(a, a)-⾮非⾃自反关系•∀ a ∈ A, 有(a, a) ∉ R, 称R 是A 上的⾮非⾃自反关系•R = {(1, 2), (1, 1), (2, 2), (3, 3)}, 为⾮非⾃自反关系，且 为⾮非⾃自反关系•在关系阵中：(1) ⾃自反: m ii = 0 (2) ⾮非⾃自反: m ii = 0•在有向图中：(1) ⾃自反: 所有顶点都是恒等环 (2) ⾮非⾃自反: 有顶点不是恒等环-对称性•对称关系：∀ aRb 有bRa ，则R 是A 上的对称关系•⾮非对称关系：∃ aRb, 有bRa, 称R 是A 上的⾮非对称关系0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 0⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟｜、1.2.3.4 制作2014年10⽉月27⽇日 星期⼀一-反对称关系•当a ≠ b 时, aRb 与bRa 不能同时成⽴立•在R 中, aRb 且bRa, 有a = b•如：R = {(1, 2), (4, 4)}-在关系矩阵中•对称矩阵：∀ m ij = 1 有 m ji = 1, 矩阵A 是对称矩阵 <=> A 的转置矩阵 A T = A•⾮非对称矩阵：m ii = 0, 且当m ij = 1有m ji = 0•反对称矩阵：当i ≠ i, ∀ m ij = 1有m ji = 0-在有向图中•对称：任意两个顶点间，要么没有边，要么有2个边，可⽤用下图表⽰示•⾮非对称：所有顶点都不是恒等环, 且任意两点间最多有⼀一边•反对称：任意两点最多有⼀一边-传递性•传递关系：对所有aRb, 且bRc 有aRc•定理：R 是A 上的关系, |A| = n 则R 是A 上的传递关系 <=> R 2 ≤ R•M R 2 = ⨀ = •R 2 = ∅ ≤ R•写出A = {(, ), (, )}•写出M R = ()•M R 2 = M R ⨀ M R•画出R 2的有向图•判断R 是否传递-等价关系•R 是⾃自反对称关系 0 1 0 0 0 0 0 0 0 0 0 0⎛⎝⎜⎜⎞⎠⎟⎟ 0 1 0 0 0 0 0 0 0 0 0 0⎛⎝⎜⎜⎞⎠⎟⎟ 0 0 0 0 0 0 0 0 0 0 0 0⎛⎝⎜⎜⎞⎠⎟⎟ab c•例: A = {1, 2, 3, 4}• R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (3, 4), (4, 3), (4, 4)}•M R = •m 11 = m 22 = m 33 = m 44 = 1, 则R 是⾃自反的•M R T = = M R , 则R 是对称的•M R 2 = M R ⨀ M R = = M R •R 2 = R, R 2 ∈ R, R 是传递的•例：A = Z, aRb <=> a ≣b(mod 2) 3≣5(mod 2)->3除2的余等于5除2的余•∀a ∈Z, a ≣a(mod 2), 则(a, a) ∈ R, ⾃自反•∀aRb, a ≣b(mod 2), b ≣a(mod 2), 则bRa, 对称• ∀aRb, 且bRc, a ≣b(mod 2), b = c(mod 2)有a ≣c(mod 2), 则aRc 传递-定理：P = {A 1, A 2, … A R }, 是A 的⼀一个划分, aRb <=> a 与b 在P 的同⼀一块A 之中, 则R 是A 上的⼀一个等价关系•R = {A 1×A 1∪A 2×A 2∪…∪A k ×A k }•例：A = Z, aRb <=> a ≣b(mod n ), A = {1, 2, 3, 4}, P = {{1, 2}, {3, 4}}, R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 3), (4, 4)}•★等价类: R 是等价关系(P 147,21)•若R(x) = {b | (x, b) ∈ R}, 则称R(x)是x 的等价类•如R = {(1, 1), (1, 2), (2, 1), (2 ,2)}•R(1) = {1 ,2}1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟ 1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟ 1 1 0 0 1 1 0 0 0 0 1 1 0 0 1 1⎛⎝⎜⎜⎜⎜⎞⎠⎟⎟⎟⎟•R(2) = {1, 2}-定理：R是A上的等价关系, P = {R(a) | a ∈ A}, 则P是A上的⼀一个划分，记做A/R •满⾜足：(1) a∈A 的所有并集, R(a) = A• (2)。

第四章代数代数又称为代数结构或代数系统，是用代数方法构造的数学模型。

代数系统对于研究各种数学问题和许多实际问题是很有用的，对计算机科学研究也有很大的实用意义，例如，在程序设计语言的语义研究中，数据结构的研究中，编码理论的研究中，系统生成与结构，语言代数，计算理论以及逻辑电路设计中均有重要的理论和实际意义。

§4.1 一般代数结构这一节开始讨论系统及系统的结构。

第一章与第二章着重讨论了一些集合，一般来讲，不论是什么系统，都是若干个集合按一定的条件构成。

构成的条件可以用列举法给出，更多的是由命题法和归纳法给出。

如果结出的若干个集合不是一些具体的集合，这些不具体的集合概念完全由命题来决定通用的概念，则这种构成系统的方法称为公理的方法。

所以这一节还有一个任务是向公理方法过渡。

4.1.1 代数运算关系是集合，函数是关系，函数是“单值”的关系也是集合。

下面定义的代数运算是一个特殊的函数。

定义4.1.1设X为非空集合，n∈I+，n→称为X上的n元运算，其中n为运算ω的阶(类型)，记为n ω。

①函数ω：X X②X中的每一个元素称为X上的0元运算。

当n ω＝1时，称ω为一元运算，例如实数集合R上的“负”运算；当n ω＝2时，称ω为二元运算，例如R上的“＋”和“*”运算。

二元运算在许多方面的研究中有着重要的意义，在后面二元运算用一个字母θ来表示。

实际上用的0元运算只是集合X中的某些特定的元素，例如R中的0和1。

在上一节中所定义的运算是一元运算。

由定义可以看出，所谓集合X上的n元运算，乃是指某种规则，对于X上的每一个n元序偶，规定了X中唯一的元素与之对应。

,,...,∈S，都有ω定义4.1.2设ω为X上的n元运算，S∈X，如果对于任意a a a n12,,...,‡)∈S，则称S关于ω封闭的。

(†a a a n12例如，考察自然数集合N上的加法运算“＋”，显然非负偶数集合关于“＋”是封闭的，但非负奇数关于“＋”是不封闭的。

第四章归结法原理习题与解答1. 用归结法证明：(1)(2)(3)(4)(5)(6)解(1) 首先将p→q,p→r，¬(p→q∧r)化为合取范式。

p→q⇔¬p∨qp→r⇔¬p∨r¬(p→q∧r)⇔¬(¬p∨(q∧r))⇔p∧(¬q∨¬r) 给出子句集{¬p∨q,¬p∨r,p,¬q∨¬r}的反驳如下。

⑴ ¬p∨q⑵ ¬p∨r⑶ p⑷ ¬q∨¬r⑸ q 由⑴和⑶由⑵和⑶⑹ r⑺ ¬r 由⑷和⑸⑻ □ 由⑹和⑺因此，p→q,p→r|=p→q∧r(2) 首先将p→r，q→r，¬(p∨q→r)化为合取范式。

p→r⇔¬p∨rq→r⇔¬q∨r¬(p∨q→r)⇔(p∨q)∧¬r给出子句集{¬p∨r,¬q∨r,p∨q,¬r}的反驳如下。

⑴ ¬p∨r⑵ ¬q∨r⑶ p∨q⑷ ¬r⑸ q∨r 由⑴和⑶ p→q,p→r|=p→q∧r p→r,q→r|=p∨q→r p→q∨r|=(p→q)→(p→r)p∧q→r|=(p→r)∨(q→r) p∨q∨r,p→r|=q∨r (p→q)→(p→r)|=p→(q→r)由⑵和⑸⑹ r⑺ □由⑷和⑹因此，p→r，q→r|=p∨q→r(3) 首先将p→q∨r,¬((p→q)∨(p→r))化为合取范式。

p→q∨r⇔¬p∨q∨r¬((p→q)∨(p→r))⇔¬((¬p∨q)∨(¬p∨r))⇔p∧¬q∧¬r 给出子句集{¬p∨q∨r,p,¬q,¬r}的反驳如下。

⑴ ¬p∨q∨r⑵ p⑶ ¬q⑷ ¬r⑸ q∨r 由⑴和⑵⑹ r 由⑶和⑸⑺ □ 由⑷和⑹因此，p→q∨r|=(p→q)∨(p→r)(4) 首先将p∧q→r,¬((p→r)∨(q→r))化为合取范式。