离散时间系统的z域分析
- 格式:doc
- 大小:116.00 KB
- 文档页数:4





第七章离散时间系统的Z域分析7.1 学习要求1.熟练掌握信号的Z域分析方法:Z变换的定义、收敛区及基本性质,能够应用长除法和部分分式分解法求Z反变换。
2.掌握序列的傅里叶变换的定义和基本性质,并了解Z变换与拉普拉斯变换、傅里叶变换的关系。
3.掌握离散系统响应的Z变换分析方法:深刻理解离散系统的系统函数的概念,掌握离散时间系统的时域和Z域框图与流图描述形式。
7.2 学习重点1.z变换,z反变换定义、基本性质、计算方法。
2.离散时间系统的z域分析。
3.离散时间系统的频率响应特性。
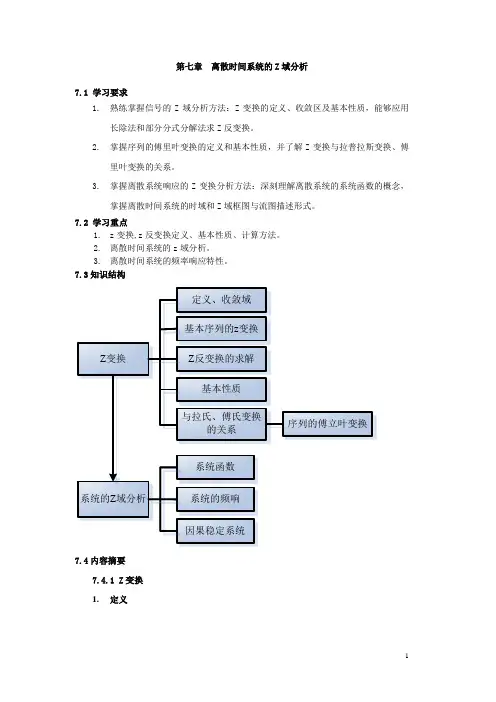
7.3知识结构7.4内容摘要7.4.1 Z变换1.定义∑∞-∞=-=n nz n x z X )()( 表示为:)()]([z X n x Z =。
2. 收敛域 (1) 有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他当0,021>>n n 时,收敛条件为0>z ;当0,021<<n n 时,收敛条件为∞<z ;当0,021><n n 时,收敛条件为∞<<z 0。
(2) 右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩当01>n 时,收敛域为1x R z >,1x R 为最小收敛半径;当01<n 时,收敛域为∞<<z R x 1。
(3) 左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他 当02<n ,收敛域为2x R z <,2x R 为最大收敛半径; 当02>n ,收敛域为20x R z <<。
(4) 双边序列双边序列指n 为任意值时,)(n x 皆有值的序列,即左边序列和右边序列之和。
其z 变换:∑∑∑∞=--∞=--∞-∞=-+==1)()()()(n n nnn nzn x zn x zn x z X双边序列的收敛域为一环形区域21x x R z R <<。


《信号与系统》课程实验报告变换。
zz z z z z F 2112)(232+++-=一、实验原理的验证 1、离散系统零极点图实验原理如下:离散系统可以用差分方程描述:∑∑==-=-Mm m Ni i m k f b i k y a 0)()(Z 变换后可得系统函数:NN MM z a z a a z b z b b z F z Y z H ----++++++==......)()()(110110 可以用root 函数可分别求零点和极点。
例7-4 求系统函数零极点图131)(45+-+=z z z z H实验结果如下:2、离散系统的频率特性实验原理如下:离散系统的频率特性可由系统函数求出,既令ωj e z =,函数freqz 可计算频率特性,调用格式是:[H ,W]=freqz(b,a,n),b 和a 是系统函数分子分母系数,n 是π-0范围内n 个等份点,默认值为512,H 是频率响应函数值,W 是相应频率点; 例7-5 系统函数z z z H 5.0)(-=10个频率点的计算结果为幅频特性曲线相频特性曲线freqz语句直接画图例7-7已知系统函数114/11)1(4/5)(----=z z z H ,画频率响应和零极点图。
零极点图幅频特性曲线相频特性曲线二、已知离散系统的系统函数如下所示:1422)(232+-++=z z z z z H试用MATLAB 实现下列分析过程: (1)求出系统的零极点位置;(2)绘出系统的零极点图,根据零极点图判断系统的稳定性; (3)绘出系统单位响应的时域波形,并分析系统稳定性与系统单位响应时域特性的关系。
(1)由计算结果可知:系统的极点为p0=-3.3028、p1=1、p2=0.3028。
由计算结果可知:系统的零点为z0=1.4142i 、z1=-1.4142i 。
(2)系统的零极点图如下:程序清单如下: a=[1 2 -4 1]; b=[1 0 2]; ljdt(a,b)p=roots(a)q=roots(b)pa=abs(p)由图可知:第一个极点(p0)在单位圆外部,第二个极点(p1)在单位圆上,第三个极点(p2)在单位圆内部,因为有一个极点在单位圆外部,故该系统是不稳定的系统(稳定系统要求极点全部在单位圆内)。


北京理工大学信号与系统实验报告6-离散时间系统的z域分析————————————————————————————————作者:————————————————————————————————日期:实验6 离散时间系统的z 域分析(综合型实验)一、 实验目的1) 掌握z 变换及其反变换的定义,并掌握MAT LAB实现方法。
2) 学习和掌握离散时间系统系统函数的定义及z 域分析方法。
3) 掌握系统零极点的定义,加深理解系统零极点分布与系统特性的关系。
二、 实验原理与方法 1. z 变换序列(n)x 的z 变换定义为(z)(n)znn X x +∞-=-∞=∑ (1)Z 反变换定义为11(n)(z)z 2n rx X dz jπ-=⎰(2)MA TLA B中可采用符号数学工具箱z trans 函数和iz trans 函数计算z 变换和z 反变换: Z=ztran s(F)求符号表达式F的z 变换。
F=iztra ns(Z)求符号表达式Z 的z 反变换 2. 离散时间系统的系统函数离散时间系统的系统函数H(z)定义为单位抽样响应h(n)的z 变换(z)(n)znn H h +∞-=-∞=∑ (3)此外连续时间系统的系统函数还可由系统输入与输出信号z 变换之比得到(z)(z)/X(z)H Y = (4)由(4)式描述的离散时间系统的系统时间函数可以表示为101101...(z)...MM NN b b z b z H a a z a z----+++=+++ (5) 3. 离散时间系统的零极点分析MATLAB 中可采用roots 来求系统函数分子多项式和分母多项式的根,从而得到系统的零极点。
此外还可采用MATL AB 中zpl ane 函数来求解和绘制离散系统的零极点分布图,zp lane 函数的调用格式为:zplane(b,a) b、a 为系统函数分子分母多项式的系数向量(行向量) zplane (z,p) z 、p为零极点序列(列向量) 系统函数是描述系统的重要物理量,研究系统函数的零极点分布不仅可以了解系统单位抽样响应的变化,还可以了解系统频率特性响应以及判断系统的稳定性; 系统函数的极点位置决定了系统的单位抽样响应的波形,系统函数零点位置只影响冲激响应的幅度和相位,不影响波形。
第7章 离散时间系统的z 域分析
1.z 变换是如何提出的?它的作用是什么?
z 变换是为分析离散时间系统而提出的一种工程分析方法,它在离散时间系统分析中的地位和作用等价于连续时间系统分析中的拉氏变换。
它可以看作为拉氏变换的推广。
z 变换定义为:()[]n
n X z x n z
∞
-=-∞
=
∑ ---- 双边z 变换 (1)
()[]n n X z x n z ∞
-==∑---- 单边z 变换 (2)
其中z 是复变量,Re Im j z z j z re Ω=+=。
而对于取样信号的拉氏变换为
()()()() ()() ()st
st s s n st n snT
n X s x t e dt x nT t nT e dt
x nT e t nT dt x nT e
δδ∞∞
∞
---∞-∞
=-∞∞
∞
--∞=-∞
∞
-=-∞
⎡⎤
==-⎢⎥⎣⎦
⎡⎤=-⎢⎥⎣⎦=
∑⎰⎰∑⎰∑ (3)
如果 [](),x n x nT =令sT z e =,可以发现式(1)和式(3)相同。
2.双边z 变换和单边z 变换时如何定义的?它们的定义域是如何确定的?收敛域的意义是什么?
z 变换定义为:()[]n
n X z x n z
∞
-=-∞
=
∑ ---- 双边z 变换 (1)
()[]n n X z x n z ∞-==∑---- 单边z 变换 (2)
z 变换收敛域就是使上述级数收敛的所有z 的取值的集合。
根据级数收敛理论,一般我们用根值判别法或比值判别法来确定z 变换收敛域, 其作用是建立序列和z 变换之间的一一对应关系。
根据序列的不同性质,序列z 变换的收敛域各不相同,具体参阅教材Page 297-298 表7-1。
3.z 变换和拉氏变换之间有什么样的关系?
具体分析见问题1中的式(1)和(3),根据两式,可以建立分析连续时间系统的拉氏变换的变量s 和分析离散时间系统的z 变换的变量z 之间的映射关系:
sT z e =
令, j z re s j σωΩ==+, 则有
, T r e T σω=Ω=, 具体见教材Page 300 表7-2 。
4.z 逆变换的求解方法有几种?在应用部分分式求解z 逆变换时,应注意什么问题?
z 逆变换的求解方法主要有三种:围线积分法(复变函数理论),幂级数展开法和部分分式展开法。
其中幂级数展开法只适用于单纯的左边序列或右边序列,而且不易得到序列的解析式,因而实际中使用不多;而围线积分法(复变函数理论)和部分分式展开法因其方法的逻辑性较强,适用于各种序列,而且便于得到序列的解析式,所以,最为我们所采纳。
在求解z 逆变换时,特别要注意极点相对于收敛域的位置,因为这关系到序列的性质,是序列的左边部分还是右边部分。
5.说明如何应用z 变换的移位性质求解差分方程。
z 变换是求解差分方程的一种有效手段和便捷的方法。
考虑到实际的系统大多是因果系统,且满足差分方程
[][]N
M
m
r m r a
y n m b x n r ==-=-∑∑
输入信号为因果信号, 即[]0,0x n n =<,
边界条件:[],y N - [1],...,[1]y N y -+-,求输出信号[]y n 。
从给定的条件可以看出,输出信号在n N <-时,输入信号为零,方程为齐次差分方程,此时的解就为齐次解(其系数由边界条件[],y N - [1],...,[1]y N y -+-)确定或者可以通过迭代法求解。
当0n ≥时,一般用单边z 变换求解差分方程。
此时,对方程两边取单边z 变换,
1
{()[]}()N
M
m
l
r m
r m l m
r a
z Y z y l z
b z X z ----==-=+
=∑∑∑
从而: 1
000
[]()()N
M
m l r
m r
m l m r N
N
m
m
m
m
m m a z y l z b z
Y z X z a
z
a
z ----==-=--==⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎣⎦
=
-
∑∑∑∑∑ 对上式求解逆z 变换,即得到方程的解[]y n (0n ≥)。
6.线性时不变离散时间系统的系统函数是如何定义的?说明它在分析和求解离散时间系统响应中的作用是什么?
线性时不变离散时间系统的系统函数()H z 的定义类似于连续时间系统的
()H s 的定义。
()
()()
Y z H z X z =
其中:(),()Y z X z 分别是系统零状态响应和输入信号的z 变换,因而()H z 在离散时间系统中的地位和作用也类似于()H s 。
(1)系统函数与差分方程的关系:
[][]N
M
m r m r a y n m b x n r ==-=-∑∑⇔ 00
()
()()
M
r
r
r N
m
m
m b z
Y z H z X z a
z -=-==
=∑∑
(2)系统函数与单位样值响应的关系:
() []H z h n ↔ (z 变换对)
极点决定[]h n 的波形性质,零点影响[]h n 的幅度和相位。
(3)系统函数与系统特性的关系:
()H z 收敛域包含单位圆 ⇔ 系统稳定 ()H z 收敛域为||, (0)z r r >≥ ⇔ 因果系统
7.离散时间信号的频谱如何定义?它具有什么特点?
离散时间信号的频谱定义为离散时间信号的傅里叶变换:
()[]j j n
n X e x n e
∞
Ω
-Ω=-∞
=
∑
其意义在于建立了离散时间信号和傅里叶变换之间的关系,从而建立了信号的时间域和频率域之间的映射关系,统一了离散时间信号与系统和连续时间信号与系统的分析方法。
离散时间信号的频谱具有周期性和连续性的特点,这是与连续时间信号频谱
的主要区别。
8.离散时间系统的频率响应是如何定义的?它的意义是什么? 如何得到离散时间系统的幅频特性和相频特性曲线?
离散时间系统的频率响应反映了离散时间系统在正弦序列激励下的稳态响应随离散信号频率的变化关系。
它定义为单位样值响应序列[]h n 的傅里叶变换,即
()()[]|()|j j n
j j n H e h n e
H e e ϕ∞
Ω
-ΩΩΩ=-∞
=
=∑
根据系统函数与单位样值响应的关系:()[] n
n H z h n z
∞
-=-∞
=∑
有
()()|j j z e H e H z ΩΩ==,
因而可以根据系统函数的零极点分布利用矢量作图的方法粗略地获得系统的幅频响应和相频响应曲线。
9.数字滤波器具有什么特点?它有什么优点?在实现时,有几种结构?各有什么特点?
在数字滤波器中,输入和输出都是离散时间序列。
数字滤波器的作用是对离散时间信号进行处理和变换,这里我们是指选频滤波器,即滤除信号中的多余频率成分的滤波器。
其优点主要有:精度高,稳定性好,灵活性大,体积小,易于集成等。
实现时,主要有三种结构:
(1)直接型:稳定性受系数影响较大,零点和极点受系数的影响很大; (2)级联型:实现的结构简单,零点和极点受系数的影响较小;
(3)并联型:实现的结构也较简单,极点受系数影响较小,但零点受系数影响较大。