工程力学--材料力学(北京科大、东北大学版)第4版第七章习题答案

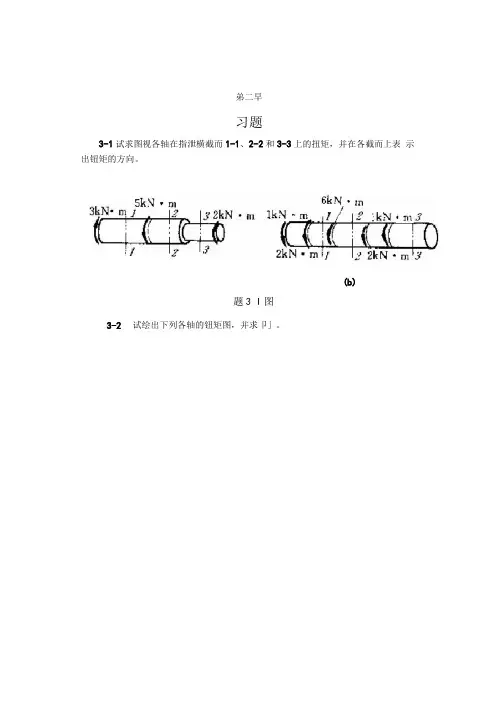
弟二早习题3-1试求图视各轴在指泄横截而1-1、2-2和3-3上的扭矩，并在各截而上表示出钮矩的方向。

(b)题3 I图3-2 试绘出下列各轴的钮矩图，并求卩」。

2mD cfr@=©=33-3 ma=2OON.m 9mb=4OON.m 9mc=6OON 9m. (b)3-4 一传动轴如图所示，已知 ma=130N ・・cm, mb=300N.cm, mc=i, md=70N.cm;^段轴的直径分别为：Dab=5cm, Dbc=7.5cm, Dcd=5cm（1） 画出扭矩图；（2） 求1 •仁2・2、3・3截而的最大切应力。

3-5图示的空心圆轴，外径D=8cm,内径d=6.25cm,承受扭矩m=1000N.m. （1） 求（2） 绘出横截面上的切应力分布图： （3）求单位长度扭转角，已知G=80000Mpa.3-6已知变截而钢轴上的外力偶矩^=1800N.m, Wf=1200N.m,试求最大切应力和最大相对扭矩。

已知G=80dbpa ・3M试绘下列各轴的扭矩(a)题3-6图3-7 一钢轴的转矩n=240/min.传递功率^=44.1kN.m.已知[^=40Mpa,=1W,6=80*MPa,试按强度和冈帔条件汁算轴的直径解：轴的直径由强度条件确左，rf>60-7wn o3-8图示实心轴通过牙嵌离合器把功率传给空心轴。

传递的功率ft=7.5kw,轴的转速n=100r/min,试选择实心轴直径占和空心轴外径“。

已知%心入5,题L8图3-9图示AB轴的转速n=120r/min,从B轮上输入功率丹=40kw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传疋。

已知锥齿轮的节圆直径=600mm：各轴直径为^-=100111111, “=80mm, “=60fnfn, KLzOlWPa,试对各轴进行强度校核。

3-10船用推进器的轴，一段是实心的，直径为280mm,另一段是空心的，其内径为外径的一半。

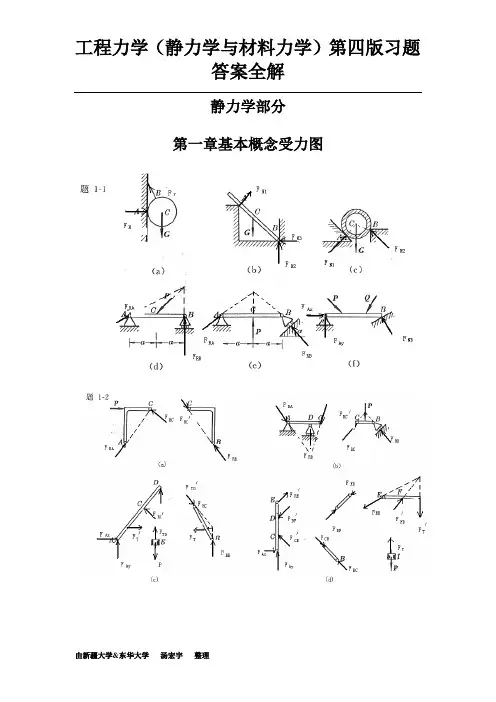
静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故：161.2R F N ==1(,)arccos 2944RY R R F F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑ 13sin 45sin 450RY F Y P P ==-=∑ 故：3R F KN == 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑ sin 300AC AB F F -=0Y =∑ cos300AC F W -=0.577AB F W =（拉力） 1.155AC F W =（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑ sin 700AB F W -=1.064AB F W =（拉力）0.364AC F W =（压力）（c ） 由平衡方程有：0X =∑ cos 60cos300AC AB F F -=0Y =∑ sin 30sin 600AB AC F F W +-=0.5AB F W = (拉力)0.866AC F W =（压力）（d ） 由平衡方程有：0X =∑ sin 30sin 300AB AC F F -=0Y =∑ cos30cos300AB AC F F W +-=0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由0x =∑cos 450RA F P -=15.8RA F KN ∴=由0Y =∑sin 450RA RB F F P +-=7.1RB F KN ∴=(b)解：受力分析如图所示：由x =∑cos 45cos 450RA RB F F P --=0Y =∑sin 45sin 450RA RB F F P -=联立上二式，得： 22.410RA RB F KNF KN ==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解：受力分析如图所示，取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CB RA F F '-= 联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q -=联立方程后解得：RD F =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得：RA F =2RB F Q P=+（3）取BCE 部分。

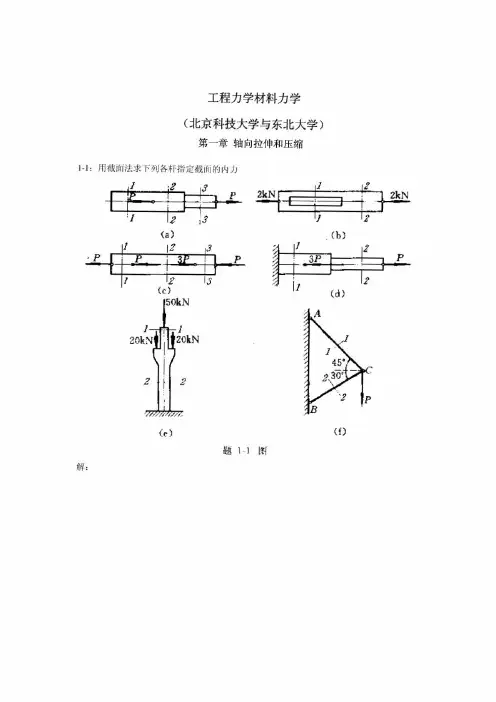
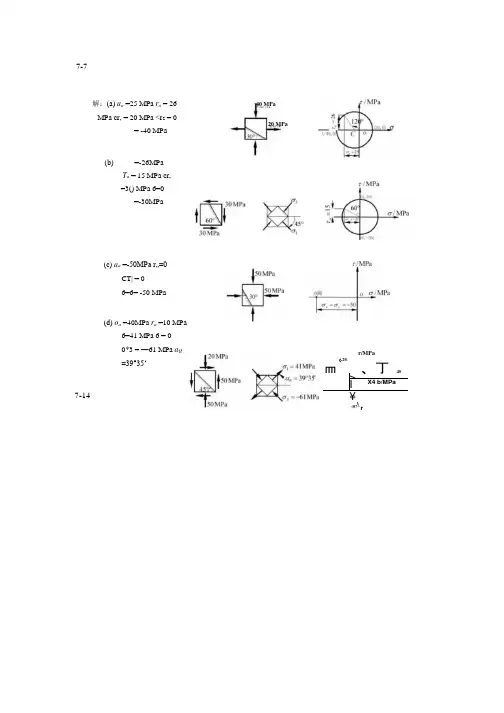
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a 所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN ，吊杆的尺寸如图b 所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS=38.1MPa1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC ACLNL EA EA σε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

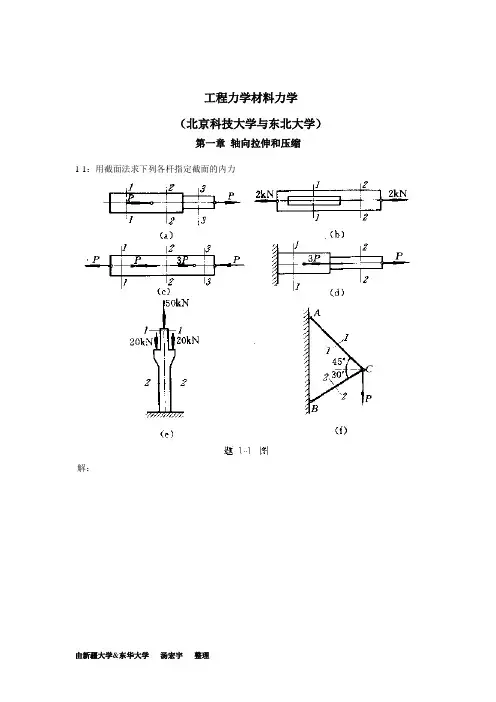
(c) a a =-50MPa r…=0CT| = 0 6=6= -50 MPa(d) o a =40MPa r a =10 MPa6=41 MPa 6 = 0 0*3 = —61 MPa a Q =39°35‘7-7 解：(a) a a =25 MPa r a = 26 MPa cr, = 20 MPa <r 2 = 0= -40 MPa (b) =-26MPa T a = 15 MPa cr, =3() MPa 6=0=-30MPa40 MPa20 MPa7-14(-20.皿、丁40> I X4 b/MPa ¥\ (0?^rr/MPa7-15单元体各面上的应力如图所示。

试用应力圆的儿何关系求主应力及最人切应力。

解：(a)由卩平面内应力值作a, b点,连接"交O•轴得圆心C (5(). 0)应力圆半径心)2+时=44.726 =50+44.7 = 94.7 MPa cr3=50-44.7 = 5.3 MPa (T2 = 50MPa2= 44.7 MPay r/MPa(b)由心平面内应力作g b点,连接血交O•轴丁•(？点，0030.故应力圆半径则: r = >/302 +402 = 506 =30 +50 = 8() MPaa2 =50 MPa a3=-20 MPa= 5() MPa(c)由图7-15 (c)yz平面内应力值作a, b点,圆心为O,半径为50,作应力圆得6 = 5() MPaa2 =-50 MPa6 =-80 MPa50 MPar/MPamax '6 一6 ,二」——=65MPa27-187-19在矩形截面钢拉伸试样的轴向拉力F = 20kN时，测得试样中段B点处与其轴线成30°方向的线应变为a. =3.25x10"。

已知材料的弹性模量£ = 210GPa ,试求泊松比解:F 20X103A " 20x10x10" = 10() MPa CT=a cos2a = —a = 75 MPa4cr|20. = cr cos2a = 25 MPa3.25X10_4 X210X 109 = (75-yx25)x IO6 v = 0.27M c = M n = 690kN- m Fsc 狂=佗 D 右=670 kN7-197-20 D= 120mm,治&hnm 的空心圆轴，两端承受一对扭转力偶矩，如图所示。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N 1=0,N 2=N 3=P(b):N 1=N 2=2kN(c):N 1=P,N 2=2P,N 3= -P(d):N 1=-2P,N 2=P(e):N 1= -50N,N 2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104, CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3=-P(d):N1=-2P,N2=P(e):N1=-50N,N2=-90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3=3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解:(1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2)∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*1041-8:解: Nll EAl l ε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max59.5MPa σσ=<1-11：解：（1）当45o α=，[]11.2σσ=>强度不够（2）当60o α=，[]9.17σσ=<强度够1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPaσ=<1-14：解： 1.78, 1.26d cm d cm==拉杆链环1-15解：BC F ==70.7kN70.70.505140F S FS σσ=∴=== 查表得：45*45*31-16解：(1)[]2401601.5s s n σσ===MPa [][]24P S P dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPaS d σπ===≤⎛⎫ ⎪⎝⎭1-17解：（1）2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ==300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F SF S Nσσ===='61544014.521542390F n F ===≈1-18解：P=119kN1-19解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kNP kN σ=====同理所以最大载荷84kN1-20解：P=33.3kN1-21解：71,,12123A B C P F F P F P ===1-22解：10MAX MPaσ=-1-23解：A B X R R R=∴==∑t r l l ∆=∆t AB l l tα∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1一螺栓连接如图所示，已知P=200kN ，=2cm ，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。

工程力学答案东北大学【篇一：工程力学材料力学第四版(北京科技大学与东北大学)习题答案】（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):n1=0,n2=n3=p(b):n1=n2=2kn(c):n1=p,n2=2p,n3= -p(d):n1=-2p,n2=p(e):n1= -50n,n2= -90n(f):n1=0.896p,n2=-0.732p注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力p=850kn，试计算大钟拉杆的最大静应力。

p850kn?2s1p850kn?2s2max=35.3mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kn，吊杆的尺寸如图b所示。

解：90p?s10.065*0.045=15.4mpamax=15.4mpa1-4：一桅杆起重机如图所示，起重杆ab为一钢管，其外径d=20mm,内径d=18mm;钢绳cb的横截面面积为0.1cm2。

已知起重量p=2000n，试计算起重机杆和钢丝绳的应力。

解：受力分析得：f1*sin15=f2*sin45f1*cos15=p+f2*sin451-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量p=2000n.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,h=65mm,钉孔直径d=30mm.试求链板的最大应力.【篇二：东北大学考试试卷工程力学】学年第学期课程名称：工程力学(长型)一、选择题 ( 27分)（每题3分。

请将答案的序号填入划线内。

）1. 一直径为d1的实心轴，另一内外径比为??d2/d2的空心轴，若两轴横截面上的扭矩和最大剪应力分别相等，则两轴的横截面积之比a1/a2有四种答案：42/3242/342/322(1??)(1??)(1??)(1??)/(1??) 1??(a)； (b) ； (c) ； (d)正确答案是。

第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa ∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3= 3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ==== AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*104 1-8:解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max 59.5MPa σσ=<1-11：解：（1）当45oα=，[]11.2σσ=>强度不够 （2）当60oα=，[]9.17σσ=< 强度够 1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPa σ=<1-14：解：1.78, 1.26d cm d cm ==拉杆链环1-15 解：BC F ==70.7 kN70.70.505140F S FS σσ=∴=== 查表得： 45*45*31-16解：(1)[]2401601.5s s n σσ===MPa[][]24P SP dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPa S d σπ===≤⎛⎫⎪⎝⎭1-17 解：（1）2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭ 78.4AC F MPa S σ== 300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F S F S Nσσ===='61544014.521542390F n F ===≈1-18 解：P=119kN1-19 解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kN P kN σ=====同理所以最大载荷 84kN1-20 解： P=33.3 kN1-21 解：71,,12123A B C P F F P F P ===1-22 解：10MAX MPa σ=-1-23 解：A B X R R R =∴==∑t r l l ∆=∆ t AB l l t α∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1 一螺栓连接如图所示，已知P=200 kN ， =2 cm ，螺栓材料的许用切应力[τ]=80Mpa ，试求螺栓的直径。

工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析标准化文件发布号：（9312-EUATWW-MWUB-WUNN-INNUL-DDQTY-KII工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=,N2=注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==σ2=2228504P kN S d π= =∴σmax =1-3：试计算图a 所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN ，吊杆的尺寸如图b 所示。

解：下端螺孔截面：σ1=19020.065*0.045P S ==上端单螺孔截面：σ2=2PS =上端双螺孔截面：σ3= 3PS=∴σmax=1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=σBC=22FS= MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*=180mm2S2=(H-d)*t=(65-30)*=∴σmax=2FS=1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△l AC=NLEA=ACLEAσ=△l CD=CDL EAσ=0△L DB=DBL EA σ=(2) ∴AB l∆=1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===*104,CB CB CB L NL EA EA σε===*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。