下载文档原格式
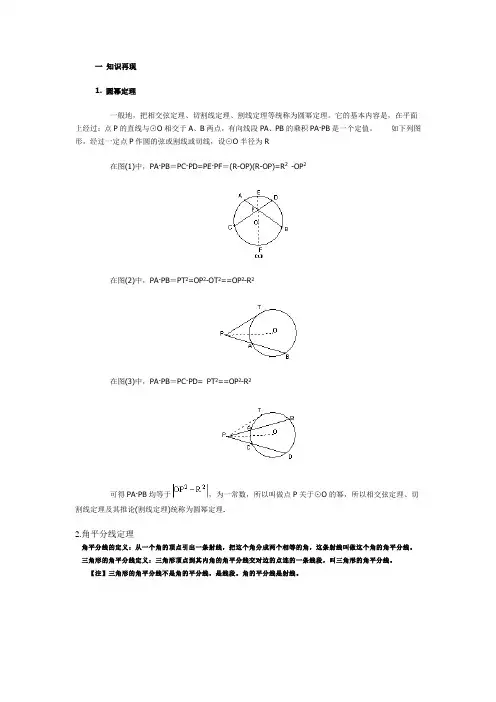
一知识再现1. 圆幂定理一般地，把相交弦定理、切割线定理、割线定理等统称为圆幂定理。
它的基本内容是，在平面上经过；点P的直线与⊙O相交于A、B两点，有向线段PA、PB的乘积PA·PB是一个定值。
如下列图形，经过一定点P作圆的弦或割线或切线，设⊙O半径为R在图(1)中，PA·PB＝PC·PD=PE·PF＝(R-OP)(R-OP)=R2-OP2在图(2)中，PA·PB＝PT2=OP2-OT2==OP2-R2在图(3)中，PA·PB＝PC·PD= PT2==OP2-R2可得PA·PB均等于，为一常数，所以叫做点P关于⊙O的幂，所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理.2.角平分线定理角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线。
三角形的角平分线定义：三角形顶点到其内角的角平分线交对边的点连的一条线段，叫三角形的角平分线。
【注】三角形的角平分线不是角的平分线，是线段。
角的平分线是射线。
■拓展：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心)。
■定理1：在角平分线上的任意一点到这个角的两边距离相等。
■逆定理：在一个角的内部（包括顶角），且到这个角的两边距离相等的点在这个角的角平分线上。
■定理2：三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例，如：在△ABC 中，BD 平分∠ABC ，则AD ：DC=AB ：BC 3.平行线分线段定理定理 三条平行线截两条直线，所得的对应线段成比例.二 例题讲解例1如图4AB 是⊙O 的弦，P 是AB 上一点，AB = 10cm ，P A : PB = 2 : 3，OP = 5cm ，则⊙O 的半径等于 ．解析：设⊙O 的半径为R ．∵AB = 10cm ，P A : PB = 2 : 3，∴PA = 4 cm ，PB = 6 cm ． 由相交弦定理，得P A ·PB = PC ·PD = R 2－OP 2，即4×6 = R 2－52． 所以，R = 7． 故⊙O 的半径等于7 cm ． 例2．如图5，已知P AC 为⊙O 的割线，连接PO 交⊙O 于B ，PB = 2，OP = 7，P A= AC ，则P A 的长为（ ）A ．7B ．23C ．14D ．32解析：延长PO 交⊙O 于D ．∵PB = 2，OP = 7，∴OB = 5，即PC = 12． 由切割线定理的推论，得 P A ·AC = PB ·PC ． ∵P A = AC ，∴2 P A 2 = 2×12． 所以，P A = 23．故应选B ．一、“四心”分类讨论1、外心三解形三条垂直平分线的交点叫做三角形的外心，即外接圆圆心。
圆幂定理圆幂定理是对、及（切割线定理推论）以及它们推论统一归纳的结果。
=PO^2-R^2（该结论为）所以圆内的点的幂为负数，圆外的点的幂为正数，圆上的点的幂为零。
相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。
切定理：从圆外一点引圆的和割线，是这点到割线与圆交点的两条线段长的。
割线定理：从圆外一点P引两条割线与圆分别交于A、B；C、D，则有PA·PB=PC·PD。
统一归纳：过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于A、B（可重合，即切线），L2与圆交于C、D（可重合），则有PA·PB=PC·PD。
问题1相交弦定理：圆内的两条相交弦,被交点分成的两条线段长的乘积相等。
证明：连结AC，BD，由的推论，得∠A=∠D，∠C=∠B。
∴△PAC∽△PDB∴PA/PD=PC/PB∴PA·PB=PC·PD问题2割线定理：从圆外一点P引两条割线与圆分别交于则有PA·PB=PC·PD，当PA=PB，即直线AB重合，即PA切线时得到切线定理PA^2=PC·PD证明：（令A在P、B之间，C在P、D之间）∵ABCD为∴∠CAB+∠CDB=180°又∠CAB+∠PAC=180°∴∠PAC=∠CDB∵∠APC公共∴△APC∽△DPB∴PA/PD=PC/PB∴PA·PB=PC·PD切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT^2=PA·PB（切割线定理）推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言：∵PBA、PDC是⊙O的割线∴PD·PC=PA·PB（切割线定理推论）问题3过点P任作直线交定圆于两点A、B，证明PA·PB为定值（圆幂定理）。
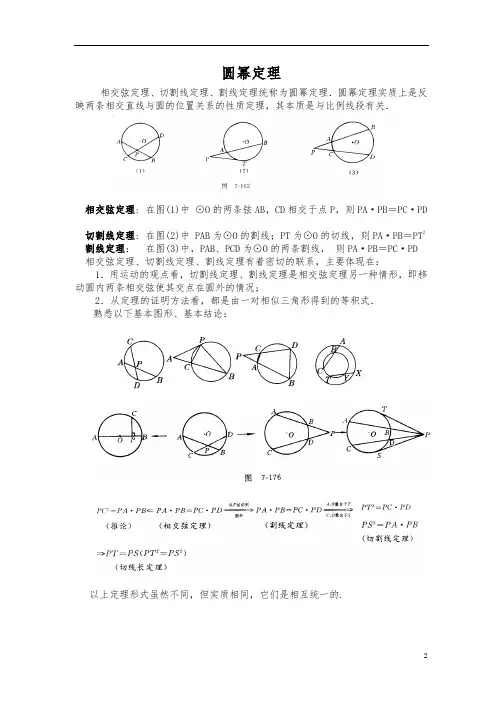
圆幂定理相交弦定理、切割线定理、割线定理统称为圆幂定理．圆幂定理实质上是反映两条相交直线与圆的位置关系的性质定理，其本质是与比例线段有关．相交弦定理: 在图(1)中⊙O的两条弦AB，CD相交于点P，则PA·PB＝PC·PD切割线定理: 在图(2)中 PAB为⊙O的割线；PT为⊙O的切线，则PA·PB＝PT2割线定理：在图(3)中，PAB、PCD为⊙O的两条割线，则PA·PB＝PC·PD 相交弦定理、切割线定理、割线定理有着密切的联系，主要体现在：1．用运动的观点看，切割线定理、割线定理是相交弦定理另一种情形，即移动圆内两条相交弦使其交点在圆外的情况；2．从定理的证明方法看，都是由一对相似三角形得到的等积式．熟悉以下基本图形、基本结论：以上定理形式虽然不同，但实质相同，它们是相互统一的.【例题求解】练习1 已知P 为⊙O 外一点，OP 与⊙O 交于点A ，割线PBC 与⊙O 交于点B ，C ，且PB ＝BC.如果OA ＝7，PA ＝2，求PC 的长.练习2 如图7-175，⊙O 和⊙O ′都经过点A 和B ，PQ 切⊙O 于P ，交⊙O ′于Q ，M ，交AB 的延长线于N.求证：PN 2＝NM ·NQ.【例1】 如图，PT 切⊙O 于点T ，PA 交⊙O 于A 、B 两点，且与直径CT 交于点D ，CD=2，AD=3，BD=6，则PB= ． (成都市中考题)思路点拨 综合运用圆幂定理、勾股定理求PB 长．注：比例线段是几何之中一个重要问题，比例线段的学习是一个由一般到特殊、不断深化的过程，大致经历了四个阶段： (1)平行线分线段对应成比例； (2)相似三角形对应边成比例；(3)直角三角形中的比例线段可以用积的形式简捷地表示出来； (4)圆中的比例线段通过圆幂定理明快地反映出来．【例2】 如图，在平行四边形ABCD 中，过A 、B 、C 三点的圆交AD 于点E ，且与CD 相切，若AB=4，BE=5，则DE 的长为( ) (全国初中数学联赛题)A ．3B ．4C ．415D ．516思路点拨 连AC ，CE ，由条件可得许多等线段，为切割线定理的运用创设条件． 注：圆中线段的算，常常需要综合相似三角形、直角三角形、圆幂定理等知识，通过代数化获解，加强对图形的分解，注重信息的重组与整合是解圆中线段计算问题的关键．【例3】 如图，△ABC 内接于⊙O ，AB 是∠O 的直径，PA 是过A 点的直线，∠PAC=∠B ．(1)求证：PA 是⊙O 的切线；(2)如果弦CD 交AB 于E ，CD 的延长线交PA 于F ，AC=8，CE ：ED=6：5， AE ：BE=2：3，求AB 的长和∠ECB 的正切值． (北京市海淀区中考题)思路点拨直径、切线对应着与圆相关的丰富知识．(1)问的证明为切割线定理的运用创造了条件；引入参数x、k处理(2)问中的比例式，把相应线段用是的代数式表示，并寻找x与k的关系，建立x或k的方程．【例4】如图，P是平行四边形AB的边AB的延长线上一点，DP与AC、BC分别交于点E、E，EG是过B、F、P三点圆的切线，G为切点，求证：EG=DE(四川省竞赛题) 思路点拨由切割线定理得EG2=EF·EP，要证明EG=DE，只需证明DE2=EF·EP，这样通过圆幂定理把线段相等问题的证明转化为线段等积式的证明．注：圆中的许多问题，若图形中有适用圆幂定理的条件，则能化解问题的难度，而圆中线段等积式是转化问题的桥梁．需要注意的是，圆幂定理的运用不仅局限于计算及比例线段的证明，可拓展到平面几何各种类型的问题中．【例5】如图，以正方形ABCD的AB边为直径，在正方形内部作半圆，圆心为O，DF切半圆于点E，交AB的延长线于点F，BF＝4．求：(1)cos∠F的值；(2)BE的长． (成都市中考题)思路点拨解决本例的基础是：熟悉圆中常用辅助线的添法(连OE，AE)；熟悉圆中重要性质定理及角与线段的转化方法．对于(1)，先求出EF，FO值；对于(2)，从△BE F∽△EAF，Rt△AEB入手．拓展练习：1．如图，PT是⊙O的切线，T为切点，PB是⊙O的割线，交⊙O于A、B两点，交弦CD于点M，已知CM=10，MD=2，PA=MB=4，则PT的长为．2．如图，PAB、PCD为⊙O的两条割线，若PA=5，AB=7，CD=11，则AC：BD= ．3．如图，AB是⊙O的直径，C是AB延长线上的一点，CD是⊙O的切线，D为切点，过点B作⊙O的切线交CD于点F，若AB=CD=2，则CE= ．4．如图，在△ABC 中，∠C=90°，AB=10，AC=6，以AC 为直径作圆与斜边交于点P ，则BP 的长为( )A ．6．4B ．3．2C ．3．6D ．85．如图，⊙O 的弦AB 平分半径OC ，交OC 于P 点，已知PA 、PB 的长分别为方程024122=+-x x 的两根，则此圆的直径为( )A ．28B ．26C ．24D ．226．如图，⊙O 的直径Ab 垂直于弦CD ，垂足为H ，点P 是AC 上一点(点P 不与A 、C 两点重合)，连结PC 、PD 、PA 、AD ，点E 在AP 的延长线上，PD 与AB 交于点F ，给出下列四个结论：①CH 2=AH ·BH ；②AD ＝AC ：③AD 2=DF ·DP ；④∠EPC=∠APD ，其中正确的个数是( )A ．1B ．2C ．3D ．4 7．如下图，BC 是半圆的直径，O 为圆心，P 是BC 延长线上一点，PA 切半圆于点A ，AD ⊥BC 于点D ．(1)若∠B=30°，问AB 与AP 是否相等?请说明理由； (2)求证：PD ·PO=PC ·PB ；(3)若BD ：DC=4：l ，且BC ＝10，求PC 的长．8．如上图，已知PA 切⊙O 于点A ，割线PBC 交⊙O 于点B 、C ，PD ⊥AB 于点D ，PD 、AO 的延长线相交于点E ，连CE 并延长交⊙O 于点F ，连AF ． (1)求证：△PBD ∽△PEC ；(2)若AB=12，tan ∠EAF=32，求⊙O 的半径的长．⌒⌒⌒9．如上图，已知AB 是⊙O 的直径，PB 切⊙O 于点B ，PA 交⊙O 于点C ，PF 分别交AB 、BC 于E 、D ，交⊙O 于F 、G ，且BE 、BD 恰哈好是关于x 的方程0)134(622=+++-m m x x (其中m 为实数)的两根．(1)求证：BE=BD ；(2)若GE ·EF=36，求∠A 的度数．10．如图，△ABC 中，∠C=90°，O 为AB 上一点，以O 为圆心，OB 为半径的圆 与AB 相交于点E ，与AC 相切于点D ，已知AD=2，AE=1，那么BC= ．11．如图，已知A 、B 、C 、D 在同一个圆上，BC=CD ，AC 与BD 交于E ，若AC=8，CD=4，且线段BE 、ED 为正整数，则BD= ．12．如图，P 是半圆O 的直径BC 延长线上一点，PA 切半圆于点A ，AH ⊥BC 于H ，若PA=1，PB+PC=a (a >2)，则PH=( )A ．a2B ．a 1C ．2aD ．3a13．如图，△ABC 是⊙O 的内接正三角形，弦EF 经过BC 的中点D ，且EF ∥AB ， 若AB=2，则DE 的长为( )A ．21 B ．215- C ．23D ．114．如图，已知AB为⊙O的直径，C为⊙O上一点，延长BC至D，使CD=BC，CE⊥AD于E，BE交⊙O于F，AF交CE于P，求证：PE=PC． (太原市竞赛题)15．已知：如图，ABCD为正方形，以D点为圆心，AD为半径的圆弧与以BC为直径的⊙O相交于P、C两点，连结AC、AP、CP，并延长CP、AP分别交AB、BC、⊙O 于E、H、F三点，连结OF．(1)求证：△AEP∽△CEA；(2)判断线段AB与OF的位置关系，并证明你的结论；(3)求BH:HC (四川省中考题)16．如图，PA、PB是⊙O的两条切线，PEC是一条割线，D是AB与PC的交点，若PE=2，CD=1，求DE的长．(国家理科实验班招生试题)。
圆幂定理相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。
或：经过圆内一点引两条弦,各弦被这点所分成的两段的积相等。
定理圆内的两条相交弦，被交点分成的两条线段长的积相等。
（经过圆内一点引两条弦，各弦被这点所分成的两段的积相等）几何语言：若弦AB、CD交于点P则PA·PB=PC·PD（相交弦定理）概述相交弦定理为圆幂定理之一，其他两条定理为：切割线定理割线定理2证明证明：连结AC，BD由圆周角定理的推论，得∠A=∠D，∠C=∠B。
（圆周角推论2：同(等)弧所对圆周角相等。
）∴△PAC∽△PDB∴PA∶PD=PC∶PB，PA·PB=PC·PD注：其逆定理可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性。
其逆定理也可用于证明四点共圆。
P 不是圆心3比较相交弦定理、切割线定理及割线定理（切割线定理推论）以及他们的推论统称为圆幂定理.一般用于求线段长度。
4相交弦定理推论定理如果弦与直径垂直相交，那么弦的一半是它所分直径所成的两条线段的比例中项。
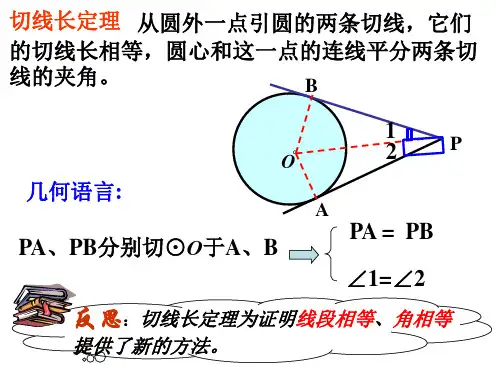
说明几何语言：若AB是直径，CD垂直AB于点P,则=PA·PB（相交弦定理推论）切割线定理切割线定理：从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.是圆幂定理的一种.切割线定理示意图几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT²=PA·PB(切割线定理)推论:从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言：∵PT是⊙O切线，PBA，PDC是⊙O的割线∴PD·PC=PA·PB（切割线定理推论）(割线定理）由上可知:PT²=PA·PB=PC·PD2证明切割线定理证明:设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT²=PA·PB证明：连接AT, BT∵∠PTB=∠PAT（弦切角定理 )切割线定理的证明∠APT=∠APT（公共角)∴△PBT∽△PTA（两角对应相等,两三角形相似)则PB：PT=PT：AP即：PT²=PB·PA3比较相交弦定理、切割线定理及割线定理（切割线定理推论)以及他们的推论统称为圆幂定理。
