六年级数学上—第1讲：分数乘法(一)

分数乘法知识点归类与练习一、分数乘法（一）分数乘法的意义：1、分数乘整数与整数乘法的意义相同。

都是求几个相同加数的和的简便运算。

2、分数乘分数是求一个数的几分之几是多少。

（二）分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子，分母不变。

（整数和分母约分）2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母。

3、为了计算简便，能约分的要先约分，结果化成最简分数。

注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

（三）规律：（乘法中比较大小时）一个数（0除外）乘大于1的数，积大于这个数。

一个数（0除外）乘小于1的数（0除外），积小于这个数。

一个数（0除外）乘1，积等于这个数。

（四）整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律： a × b = b × a乘法结合律： ( a × b )×c = a × ( b × c )乘法分配律： （ a + b ）×c = a c + b c乘法分配率逆运算： a c + b c=（ a + b ）×c中考考点1：分数的乘法计算此类题在中考中的考查多为基础性题目，一般不单独命题，题型有选择题、填空题和计算题，解决这类问题需牢记分数乘法的运算法则，灵活的运用乘法的运算律进行简便运算。

例1：316967⨯ 练习1：489623⨯➢ 分数简便运算常见题型第一种：连乘——乘法交换律的应用例题：1）1374135⨯⨯ 2）56153⨯⨯ 3）267831413⨯⨯ 涉及定律：乘法交换律 b c a c b a ⋅⋅=⋅⋅基本方法：将分数相乘的因数互相交换，先行运算。

第二种：乘法分配律的应用例题：1）27)27498(⨯+ 2）4)41101(⨯- 3）16)2143(⨯+ 涉及定律：乘法分配律 bc ac c b a ±=⨯±)(基本方法：将括号中相加减的两项分别与括号外的分数相乘，符号保持不变。

新人教版数学六年级上册第一单元《分数乘法》说课稿各位老师:大家好，今天我说课的内容是:人教版小学数学第一单元的内容《分数乘法》的第一部分--分数乘以整数。

我将从说教材、说教学法、说教学过程这三方面展开。

一、说教材(一)教材地位及作用1、地位《分数乘法》是人教实验版六年制上册第一单元的分数乘法的第一课时的内容。

这部分内容的学习是在学生已经学习了整数乘法的意义和分数加法计算的基础上进行的。

在这个内容中，分数乘整数的意义和整数乘整数的意义相同，都是求几个相同加数的和的简便运算，只是这里的相同加数变成了分数，同时分数乘整数又是分数乘分数、分数乘加、乘减混合运算的基础，因此必须使学生切实掌握好。

2、作用本部分教材内容是继以前学过的分数的加法和减法后的又一分数运算，它既与整数的乘法有着内在的联系，也是后期进一步学习分数乘以分数的乘法的基础。

(二) 教学目标依据《课标》的要求,结合我对教材的理解和对学情的分析，确定了以下教学目标:1.知识与技能:能理解分数乘以整数的计算法则，熟练掌握它的运用。

2.过程与方法:创设故事情景，导入问题，引入新课;在教学过程中，通过学生的自主操作和探究，探寻分数乘法的意义，总结出分数乘以整数的计算法则;并利用课堂习题练习和闯关练习题，使学生在实际解题中理解和掌握其运算法则，以及熟练计算涉及约分与化简的计算题，，以及运用所学知识解决实际问题的能力，渗透数形结合的数学思想3.情感态度与价值观:通过情境故事进入课堂问题，使学生感受生活中处处有数学，进一步激发学生的学习兴趣。

(三)教学重点与难点根据教学大纲的要求和教学目标，以及我对学情的分析，确定了以下重难点。

重点:掌握分数乘以整数的计算法则，并会在计算题中加以运用。

难点:在计算分数乘以整数的式子中，涉及约分与化简的计算题的运算。

二、说教学法(一)说教法为了完成以上教学目标，突出重难点，根据本阶段学生的认知特点和本节课教学内容，我在课前准备了线段单位“1”纸和PPT两种教具。

六年级数学上册：《分数的乘法》 知识点+练习一、分数乘法（一）分数乘法的意义：1、分数乘整数与整数乘法的意义相同。

都是求几个相同加数的和的简便运算。

例如： 1、 98×5表示（ ）。

2、83＋83＋83=（ ）×（ ）=（ ） 83＋83＋83＋83=（ ）×（ ）=（ ）=（ ）3、24个32是多少？ 145吨的7倍是多少吨？ 2、分数乘分数是求一个数的几分之几是多少。

例如： 1、 98×43表示的意义是（ ）。

2、125吨的32是多少吨？3、一根绳子长109米，3根这样的绳子共长（ ）米；这根绳子的31长（ ）米。

（二）分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子，分母不变。

（整数和分母约分）例如：1、72×3 53×6 214×9 103×5 1611×122、52米=（ ）厘米 32时=（ ）分 107千克=（ ）克 算式： 2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母。

例如：152×85 3914×2813 4532×2815 65×25122110×533、为了计算简便，能约分的要先约分，再计算。

注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

例如：32×143 83×154 2625×1513 6313×3914 85×52（三）规律：（乘法中比较大小时）一个数（0除外）乘大于1的数，积大于这个数。

一个数（0除外）乘小于1的数（0除外），积小于这个数。

一个数（0除外）乘1，积等于这个数。

例如：65×2 ○65 8×117○8 54×1 ○54 43×53 ○53 87×56○87×65（五）整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

第一单元 分数乘法分数乘法的意义 分数乘法的计算法则 积与因数的关系 分数乘法混合运算 与整数乘法的意义相同，都是求几个相同加数的 和的简易运算 一个数乘分数的意义是求一个数的几分之几是多少 分数与整数相乘分数与分数相乘 分子与整数相乘的积做分子，分母不变 整数和分母约分 用分子相乘的积做分子，分母相乘的积做分母 为了计算简易，能约分的要先约分，再计算 小数乘分数，可以先把小数化为分数，也可以把 分数化成小数再计算（建议把小数化分数再计 算） 当带分数进行乘法计算时，要先把带分数化成假 分数再进行计算 一个数（0除外）乘大于1的数，积大于这个数。

a ×b=c,当b >1时，c>a 。

一个数（0除外）乘小于1的数，积小于这个数。

a ×b=c,当b <1时，c<a(b≠0)。

一个数（0除外）乘等于1的数，积等于这个数。

a ×b=c,当b =1时，c=a 。

在进行因数与积的大小比较时，要注意因数为0时的特殊情况。

分数混合运算的运算顺序和整数的运算顺序相同整数乘法的交换律、结合律和分配律，对于分数 乘法也同样适用 乘法交换律：a×b = b×a乘法结合律：( a×b )×c = a×( b×c )乘法分配律：( a + b )×c = a c + b c分数乘法的解决问题 画线段图找单位“1”写数量关系式的技巧“的”相当于“×”，“占”、“相当于”“是”、“比”是“=”分率前是“的”字：用单位“1”的量×分率=部分量 两个量的关系：画两条线段图，先画单位一的量，注意两条线段的左边要对齐部分和整体的关系：画一条线段图。

单位“1”在分率句中分率的前面在“占”、“是”、“比”“相当于”的后面有没有“比”字句的问题（比少）：单位“1”的量×(1-分率)=比较量（比多）：单位“1”的量×(1+分率)=比较量求一个数的几倍是多少 求一个数的几分之几是多少 用一个数×几分之几求几个几分之几是多少 用几分之几×个数求已知一个部分量是总量的几分之几，求另一个 部分量的方法 单位“1”的量×(1-分率)=另一个部分量 单位“1”的量-已知占单位“1”的几分之几的部分量=要求的部分量 用一个数×几倍。

第1单元分数乘法第1课时分数乘法的意义（1）【教学内容】教材第2页例1。

【教学目标】知识与技能：在学生已有的分数加法及分数基本意义的基础上，结合生活实例，通过对分数连加算式的研究，使学生理解分数乘整数的意义，掌握分数乘整数的计算方法，能够应用分数乘整数的计算法则，比较熟练地进行计算。

过程与方法：通过观察比较，指导学生通过体验，归纳分数乘整数的计算法则，培养学生的抽象概括能力。

情感、态度与价值观：引导学生探求知识的内在联系，激发学生学习兴趣。

通过演示，使学生初步感悟算理，并在这过程中感悟到数学知识的魅力，领略到美。

【重点难点】重点：理解分数乘整数的意义，掌握分数乘整数的计算方法。

难点：总结分数乘整数的计算法则。

【导学过程】【情景导入】（一）探索分数乘整数的意义1.教学例1（课件出示情景图）师：仔细观察，从图中能得到哪些数学信息？这里的“个”表示什么？你能利用已学知识解决这个问题吗？（学生独立思考）师：想一想，你还能找出不一样的方法验证你的计算结果吗？2.小组交流，汇报结果预设：（1）（个）；（2）（个）；（3）（个）；（4）3个就是6个就是，再约分得到（个）。

（根据学生发言依次板书）3.比较分析师：我们先来比较第（1）和第（2）两种方法，请分别说说你是怎么想的？预设：生1：每个人吃个，3个人就是3个相加。

生2：3个相加也可以用乘法表示为。

提出质疑：3个相加的和可以用乘法计算吗？为什么？预设：乘法是求几个相同加数的和的简便计算，只是这里的相同加数是一个分数。

引导说出：分数乘整数的意义与整数乘法的意义相同。

（板书）师：我们再来比较第（2）和第（3）两种方法，这样算可以吗？为什么？引导说出：这两个式子都可以表示“求3个相加是多少”。

师：再来看这里的第（4）种方法，你能理解它表示的意思吗？结合图形把你的想法跟同桌进行交流。

4.归纳小结通过刚才的学习，我们知道了这三个算式解决的是同一个问题。

并且知道了分数乘整数的意义与整数乘法的意义相同。

分数乘法(思维导图+知识梳理+典例分析+高频真题+答案解析)【分数乘法-知识点归纳】1、分数乘法的意义：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算．2、乘积是1的两个数叫做互为倒数．3、分数乘法法则：（1）带分数乘法：先把带分数化成假分数，然后再乘．结果是假分数时，要把假分数化成带分数或整数．（2）（2）分数乘以分数：用分子相乘的积作为分子，用分母相乘的积作为分母．为了使计算简便，在计算的过程中，能够约分的，要约分．（3）分数乘以整数或整数乘以分数：由于任何整数（0除外）都可以化成分母是1的假分数，分数乘以整数或整数乘以分数，都可以转化成分数乘以分数的形式．因此，在计算中，是用分数的分子和整数相乘的积作为分子，分母不变．在乘的过程中，如果有可以约分的数，可以先约分，这样，可以使计算的数字缩小，从而使计算变得简便．【分数乘整数-知识点归纳】1、分子乘整数，可以求出一共有多少个这样的分数单位，而分数单位的个数其实就是分子乘整数的积，因此整数乘分子作分子。

求几个分数单位的和，分数单位不变，也就是分母不变。

2、分数乘整数的意义：分数乘整数，也是表示几个相同加数相加，与整数乘法的意义相同。

3、分数乘整数的计算方法：分数乘整数，用分子乘整数的积作分子，分母不变。

其实就是计算分数单位的个数。

【整数乘分数-知识点归纳】1、一个数乘分数的意义就是求一个数的几分之几是多少。

2、“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）3、方法总结；（1）、整数与分数相乘，用分数的分子与整数相乘，分母不变；（2）、计算时能约分的可以先约分再计算出结果。

【分数乘分数-知识点归纳】分数乘法的计算法则1、整数和分数相乘：整数和分子相乘的积作分子，分母不变。

2、分数和分数相乘：分子相乘的积作分子，分母相乘的积作分母。

【典例1】在“世界无烟日”健康知识竞赛中，小星答对了50道题，小铭答对的题数比小星少15。

六年级数学分数乘法知识点总结分数乘法是一种数学运算方法。

分数的分子与分子相乘，分母与分母相乘，能约分的要先约分，分子不能和分母乘。

你会整理六年级数学分数乘法知识点吗?下面给大家分享关于六年级数学分数乘法知识点，欢迎阅读!六年级数学分数乘法知识点(一)分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

“分数乘整数”指的是第二个因数必须是整数，不能是分数。

2、一个数乘分数的意义就是求一个数的几分之几是多少。

“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

(第一个因数是什么都可以)(二)分数乘法计算法则：1、分数乘整数的计算方法：用分子乘整数的积作分子，分母不变。

能约分的可以先约分，再计算。

(1)为了计算简便能约分的可先约分再计算。

(整数和分母约分)(2)约分是用整数和下面的分母约掉公因数。

(整数千万不能与分母相乘，计算结果必须是最简分数)。

2、分数乘分数的计算方法是：用分子相乘的积做分子，用分母相乘的积作分母。

(分子乘分子，分母乘分母)(1)如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

(2)分数化简的方法是：分子、分母同时除以它们的公因数。

(3)在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。

(约分后分子和分母必须不再含有公因数，这样计算后的结果才是最简单分数)。

(4)分数的基本性质：分子、分母同时乘或者除以一个相同的数(0除外)，分数的大小不变。

(三)积与因数的关系：一个数(0除外)乘大于1的数，积大于这个数。

a×b=c,当b&gt;1时，c&gt;a。

一个数(0除外)乘小于1的数，积小于这个数。

a×b=c,当b1时，c一个数(0除外)乘等于1的数，积等于这个数。

a×b=c,当b=1时，c=a。

在进行因数与积的大小比较时，要注意因数为0时的特殊情况。

分数乘法第 1 节 分数乘法运算【知识梳理】一、分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

注：“分数乘整数”指的是第二个因数必须是整数，不能是分数。

例如：53×7表示: 求7个53的和是多少？ 或表示：53的7倍是多少？ 2、一个数乘分数的意义就是求一个数的几分之几是多少。

注：“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以） 例如：53×61表示: 求53的61是多少？ 9 × 61表示: 求9的61是多少？ A × 61表示: 求a 的61是多少？ 二、分数乘法计算法则：1、分数乘整数的运算法则是：分子与整数相乘，分母不变。

注：（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

（整数千万不能与分母相乘，计算结果必须是最简分数）2、分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

（分子乘分子，分母乘分母）注：（1）如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子、分母同时除以它们的最大公因数。

（3）在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。

（约分后分子和分母必须不再含有公因数，这样计算后的结果才是最简单分数）（4）分数的基本性质：分子、分母同时乘或者除以一个相同的数（0除外），分数的大小不变。

三、积与因数的关系：一个数（0除外）乘大于1的数，积大于这个数。

a ×b=c,当b >1时，c>a.一个数（0除外）乘小于1的数，积小于这个数。

a ×b=c,当b <1时，c<a (b ≠0). 一个数（0除外）乘等于1的数，积等于这个数。

a ×b=c,当b =1时，c=a .注：在进行因数与积的大小比较时，要注意因数为0时的特殊情况。

第一讲：分数乘法（上）【知识点一】分数的基本性质1、分数乘整数的意义：求几个相同加数和的简便运算例：512×6，表示（ ），还可以表示（ ）。

注意： 求几个相同分数的和是多少 或 求一个分数的几倍是多少 就用 这个分数ד几”。

例：求3个112是多少，即可以列式（ ）。

练习：1、685⨯的意义是（ ），或（ ），得（ ）。

2、计算下列各题并说出计算方法。

9×718 = 347 ×28= 130×12 = 注意：分数的结果必须是最简分数。

2、分数乘分数的意义：是求一个数的几分之几是多少。

例如： 27 ×512 ，表示：27 的512是多少。

例 题：（说说计算方法及意义和图） 79×32= 32×23= 47×47= 3、（1）分数乘分数的计算方法也适用于小数乘分数，先把小数化成分数，再根据分数成分数的计算方法，然后计算。

例如：1417121715.0=⨯=⨯。

（2）分数乘分数，这里的分数也可以是带分数，计算时先把带分数化成假分数，再根据分数成分数的计算方法，然后计算。

例如：157513751312=⨯=⨯。

分数乘分数的简便算法也适用于分数连乘法。

例如281578315327158332=⨯⨯⨯⨯=⨯⨯。

例 题 34 ×815 ×310= 判断：12×14 和14×12的结果相同，意义也相同。

（ ） 4、单位换算。

412吨=（ ）千克 65小时=（ ）分 43分=（ ）秒 257平方米=（ ）平方分米 总结：5.常考填空题比20米多43是（ ）米 100米增加52是（ ）米 【知识点二】因数与积的大小关系1、比较大小，并说说你发现了什么规律 3231⨯○31 2152⨯○52 32×1○32 5×45○5 0×31○31总结：当一个因数大于1时，积大于另一个因数（0除外）；当一个因数小于1时，积小于另一个因数（0除外）；当一个因数小于1时，积就等于另一个因数。

第一单元 分数乘法一、分数乘法（一）分数乘法的意义： 1、分数乘整数与整数乘法的意义相同。

都是求几个相同加数的和的简便运算。

例如： 98×5表示求5个98的和是多少？ 也表示98的5倍是多少？ 5×98 表示求5的98是多少 2、分数乘分数是求一个数的几分之几是多少。

例如： 98×43表示求98的43是多少？ （二）、分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子;分母不变。

（整数和分母约分）2、分数与分数相乘：用分子相乘的积做分子;分母相乘的积做分母。

3、为了计算简便;能约分的要先约分;再计算。

注意：当带分数进行乘法计算时;要先把带分数化成假分数再进行计算。

4、分数连乘的计算方法：先约分;就是把所有的分子中可与分母相约的数先约分;再用分子乘分子作积的分子;分母乘分母作积的分母。

（三）、规律：（乘法中比较大小时）一个数（0除外）乘大于1的数;积大于这个数。

a ×b=c,当b >1时;c>a一个数（0除外）乘小于1的数;积小于这个数。

a ×b=c,当b <1时;c<a (b ≠0)一个数（0除外）乘等于1的数;积等于这个数。

a ×b=c,当b =1时;c=a（四）、分数混合运算的运算顺序和整数的运算顺序相同。

（五）、整数乘法的交换律、结合律和分配律;对于分数乘法也同样适用。

乘法交换律： a × b = b × a乘法结合律： ( a × b )×c = a × ( b × c )乘法分配律： （ a + b ）×c = a c + b c二、分数乘法的解决问题 （已知单位“1”的量（用乘法）;求单位“1”的几分之几是多少）1、求一个数的几分之几是多少？（用乘法） “1”× ba = 例：甲数的53等于乙数;已知甲数是25;求乙数是多少？ 列式：25×53=15 2、（ 什么）是（什么 ）的（几）（几）。

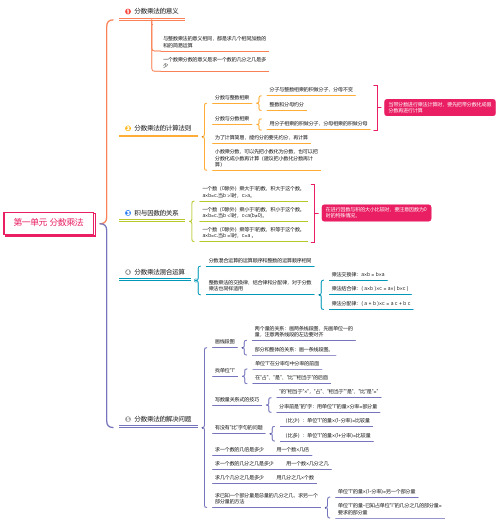
最新人教版六年级数学上册知识点汇总最新人教版六年级数学上册知识点汇总第一单元分数乘法（一）分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

“分数乘整数”指的是第二个因数必须是整数，不能是分数。

2、一个数乘分数的意义就是求一个数的几分之几是多少。

“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）（二）分数乘法计算法则：1、分数乘整数的运算法则是：分子与整数相乘，分母不变。

（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

（整数千万不能与分母相乘，计算结果必须是最简分数）。

2、分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

（分子乘分子，分母乘分母）（1）如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子、分母同时除以它们的最大公因数。

（3）在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。

（约分后分子和分母必须不再含有公因数，这样计算后的结果才是最简单分数）。

（4）分数的基本性质：分子、分母同时乘或者除以一个相同的数（0除外），分数的大小不变。

（三）积与因数的关系：一个数（0除外）乘大于1的数，积大于这个数。

a×b＝c，当b ＞1时，c＞a。

一个数（0除外）乘小于1的数，积小于这个数。

a×b＝c,当b ＜1时，c＜a(b≠0)。

一个数（0除外）乘等于1的数，积等于这个数。

a×b＝c，当b ＝1时，c＝a。

在进行因数与积的大小比较时，要注意因数为0时的特殊情况。

（四）分数乘法混合运算1、分数乘法混合运算顺序与整数相同，先乘、除后加、减，有括号的先算括号里面的，再算括号外面的。

2、整数乘法运算定律对分数乘法同样适用；运算定律可以使一些计算简便。

第一单元分数乘法（一）分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

“分数乘整数”指的是第二个因数必须是整数，不能是分数。

2、一个数乘分数的意义就是求一个数的几分之几是多少。

“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）（二）分数乘法计算法则：1、分数乘整数的运算法则是：分子与整数相乘，分母不变。

（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

（整数千万不能与分母相乘，计算结果必须是最简分数）。

2、分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

（分子乘分子，分母乘分母）（1）如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子、分母同时除以它们的最大公因数。

（3）在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。

（约分后分子和分母必须不再含有公因数，这样计算后的结果才是最简单分数）。

（4）分数的基本性质：分子、分母同时乘或者除以一个相同的数（0除外），分数的大小不变。

（三）积与因数的关系：一个数（0除外）乘大于1的数，积大于这个数。

a×b=c,当b >1时，c>a。

一个数（0除外）乘小于1的数，积小于这个数。

a×b=c,当b <1时，c<a(b≠0)。

一个数（0除外）乘等于1的数，积等于这个数。

a×b=c,当b =1时，c=a 。

在进行因数与积的大小比较时，要注意因数为0时的特殊情况。

（四）分数乘法混合运算1、分数乘法混合运算顺序与整数相同，先乘、除后加、减，有括号的先算括号里面的，再算括号外面的。

2、整数乘法运算定律对分数乘法同样适用；运算定律可以使一些计算简便。

乘法交换律：a×b=b×a 乘法结合律：(a×b)×c=a×(b×c)乘法分配律：a×(b±c)=a×b±a×c（五）倒数的意义：乘积为1的两个数互为倒数。

【导语】⽆忧考整理了⼩学六年级上册数学知识点⼤全【1-7单元】，希望对你有帮助!第⼀单元分数乘法⼀、分数乘法(⼀)分数乘法的意义：1、分数乘整数与整数乘法的意义相同。

都是求⼏个相同加数的和的简便运算。

例如：65×5表⽰求5个65的和是多少? 1/3×5表⽰求5个1/3的和是多少?2、⼀个数乘分数的意义是求⼀个数的⼏分之⼏是多少。

　例如：1/3×4/7表⽰求1/3的4/7是多少。

4×3/8表⽰求4的3/8是多少.(⼆)、分数乘法的计算法则：1、分数与整数相乘：分⼦与整数相乘的积做分⼦，分母不变。

(整数和分母约分)2、分数与分数相乘：⽤分⼦相乘的积做分⼦，分母相乘的积做分母。

注意：当带分数进⾏乘法计算时，要先把带分数化成假分数再进⾏计算。

3、为了计算简便，能约分的要先约分，再计算。

（尽量约分，不会约分的就不约，常考的质因数有11×11=121；13×13=169；17×17=289；19×19=361）4、⼩数乘分数，可以先把⼩数化为分数，也可以把分数化成⼩数再计算（建议把⼩数化分数再计算）。

　(三)、乘法中⽐较⼤⼩的规律　⼀个数(0除外)乘⼤于1的数，积⼤于这个数。

　⼀个数(0除外)乘⼩于1的数(0除外)，积⼩于这个数。

　⼀个数(0除外)乘1，积等于这个数。

(四)、分数混合运算的运算顺序和整数的运算顺序相同。

整数乘法的交换律、结合律和分配律，对于分数乘法也同样适⽤。

乘法交换律： a × b = b × a 乘法结合律： ( a × b )×c = a × ( b × c ) 乘法分配律： ( a + b )×c = a c + b c　⼆、分数乘法的解决问题(已知单位“1”的量(⽤乘法)，即求单位“1”的⼏分之⼏是多少)1、画线段图：(1)两个量的关系：画两条线段图，先画单位⼀的量，注意两条线段的左边要对齐。