定积分的几何意义

定积分的几何意义是什么定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上局部为正，x轴之下局部为负，根据cosx在[0,2π]区间的图像可知，正负面积相等，因此其代数和等于0。

定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上局部为正，x轴之下局部为负，根据cosx 在[0,2π]区间的图像可知，正负面积相等，因此其代数和等于0。

定积分的几何意义
定积分定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。

定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。

即由y=0,x=a,x=b,y=f(X)所围成图形的面积。

这个图形称为曲边梯形，特例是曲边三角形。

一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。

一个连续函数，一定存在定积分和不定积分；假设只有有限个连续点，那么定积分存在；假设有跳跃连续点，那么原函数一定不存在，即不定积分一定不存在。

定积分知识点和例题
定积分是积分的一种，是函数在某个区间上的积分和的极限。

定积分的概念起源于求图形面积和其他实际应用的问题。

下面我将列举一些定积分的知识点和例题：
知识点：
1. 定积分的定义：定积分是积分和的极限，即对一个给定区间[a,b]上的函数f(x)和任意分割法，求各小区间上函数值的点乘积和的极限。

如果存在一个常数I，对于任意给定的正数ε，总存在一个δ>0，使得当|ΔSi|<δ时，对区间[a,b]的任意分割法，和Si与I的差的绝对值都小于ε，则称I为f(x)在区间[a,b]上的定积分，记作∫abf(x)dx，其中a、b和I分别为定积分的下限、上限和值。

2. 定积分的几何意义：定积分的值等于由曲线y=f(x)与直线x=a、x=b 以及x轴所围成的曲边梯形的面积。

3. 定积分的性质：定积分的性质包括线性性质、积分中值定理、积分上限函数与被积函数的联系等。

4. 定积分的计算方法：主要包括基本初等函数的积分公式和不定积分的性质及计算方法，如换元法、分部积分法等。

例题：
1. 计算定积分∫10(x^2+1)dx的值。

2. 计算定积分∫π20(sinx+cosx)dx的值。

3. 计算定积分∫10|x-1|dx的值。

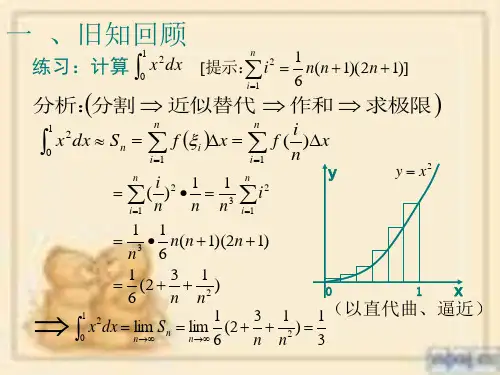
4. 计算定积分∫10x^2dx的值。

5. 计算定积分∫21(1/x)dx的值。

定 积 分教学重点:定积分的概念、定积分法求简单的定积分、定积分的几何意义． 教学难点:定积分的概念、定积分的几何意义．教学重点：掌握过程步骤：分割、以不变代变、求和、逼近（取极限）． 教学难点:过程的理解．1。

定积分的概念：一般地，设函数()f x 在区间[,]a b 上连续,用分点0121i i n a x x x x x x b -=<<<<<<<=将区间 [,]a b 等分成n 个小区间，每个小区间长度为x ∆(b a x n-∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=，作和式:11()()n n n i i i i b a S f x f nξξ==-=∆=∑∑ 如果x ∆无限接近于0（亦即n →+∞)时，上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。

记为：()ba S f x dx =⎰其中()f x 成为被积函数，x 叫做积分变量，[,]a b 为积分区间,b 积分上限，a 积分下限。

说明：（1）定积分()b a f x dx ⎰是一个常数,即n S 无限趋近的常数S (n →+∞时）称为()b af x dx ⎰，而不是n S ． (2）用定义求定积分的一般方法是：①分割：n 等分区间[],a b ; ②近似代替：取点[]1,i i i x x ξ-∈； ③求和：1()ni i b a f n ξ=-∑； ④取极限：()1()lim n b i a n i b a f x dx f n ξ→∞=-=∑⎰ （3）积分的几何意义：曲边图形面积：()ba S f x dx =⎰; 积分的物理意义: 变速运动路程21()t t S v t dt =⎰； 变力做功 ()ba W F r dr =⎰ 2．定积分的性质根据定积分的定义,不难得出定积分的如下性质：性质1a b dx b a -=⎰1 性质2⎰⎰=b a b a dx x f k dx x kf )()( （其中k 是不为0的常数） 性质31212[()()]()()b b b a a a f x f x dx f x dx f x dx ±=±⎰⎰⎰ 性质4 ()()()()bc b a a c f x dx f x dx f x dx a c b =+<<⎰⎰⎰其中例题:求曲线2x y =与0,1==y x 所围成的区域的面积 解：（1）分割：将区间[]0,1等分成n 个小区间：11i i t n n n-∆=-= （2）近似代替:2)1(1n i n s i -=∆ （3）求和: 1ni i S S ==∆∑ 从而得到S 的近似值 )12)(11(61n n s --= (4）取极限：1111115lim lim lim 112323n n n n n i i S S v n n n n →∞→∞→∞=-⎡⎤⎛⎫⎛⎫⎛⎫===---+= ⎪ ⎪⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦∑ 例1．利用定积分的定义计算dx x )1(210+⎰的值。

备考指南求平面几何图形的面积问题比较常见.对于规则的平面几何图形，可以直接利用三角形、矩形、等腰梯形、圆等的面积公式来求解；而对于不规则的曲边平面图形，直接运用平面几何图形的面积公式往往很难求得，须利用定积分的几何意义求解.定积分的几何意义是指被积函数与坐标轴围成的面积，即曲边图形的面积S =∫a bf (x )d x .若被积函数的图象位于x 轴上方,则函数的定积分为正；若位于x 轴的下方,则函数的定积分为负.定积分与曲边梯形面积的关系，如下表所示.图形阴影部分面积S ＝∫b a f (x )d x S ＝-∫baf (x )d xS ＝∫ca f (x )d x -∫bc f (x )d xS ＝∫b af (x )dx －∫b ag (x )d x ＝∫ba [f (x )－g (x )]d x利用定积分的几何意义求平面几何图形面积的步骤如下：(1)根据题意画出平面几何图形；(2)根据几何图形确定被积函数，求出图象与x 轴、y 轴的交点坐标，并求出积分的上、下限；(3)把曲边梯形的面积表示成若干个定积分的和；(4)计算定积分.例1.（1）求函数y =4-x 2在[-2,2]上的图象与x轴所围成的图形的面积；（2）求函数y =sin x 在区间[-π,π]上的图象与x 轴围成的图形的面积.解：（1）由y =4-x 2可得x 2+y 2=4(y ≥0)，该式表示的是圆心在原点、半径为2的半圆，如图1中阴影部分所示.根据定积分的几何意义可知该半圆的面积为S=∫-224-x 2d x =12π×22=2π.图1图2（2）根据题意画出图形，函数y =sin x 在区间[-π,π]上的图象与x 轴围成的图形如图2中的阴影部分所示，根据定积分的几何意义可知阴影部分的面积为∫-ππsin x d x =0.当被积函数的图象关于坐标轴或坐标原点对称时，比较容易求得几何图形的面积，直接利用定积分的几何意义和图形的对称性即可解题.例2.求曲线y 2=2x 与y =x -4所围成的图形的面积.分析：题中的图形由两条曲线围成，很难快速求得问题的答案，需将图形分割，把问题转化为求两部分图形的面积的和或差，再根据定积分的几何意义来解题.图3图4解法一：以两曲线的交点为分界点，将阴影部分分割为两部分，如图3所示.S =S 12=2∫022x x +∫28[2x -(x -4)]d x=32)|2032-(12x 2-4x )]|82=18.解法二：以x 轴为分界线，将阴影部分分割为两用定积分的几何意义求不规则平面图形黄文琴56备考指南∫226|图5图6当不能直接用定积分表示不规则平面几何图形的面积时，需采取分割图形的方法或者变换积分变量∫.反证法是解答数学问题的常用方法，是一种间接证明方法.当遇到一些从正面分析、求解较为困难的问题，或采用常规方法难以获解的问题时，采用反证法求解往往比较奏效.反证法是指假设原命题不成立，经过推理后，得到与已知条件、定理、性质等相矛盾的结论，从而证明原命题成立的方法.对于两个互相矛盾的命题和判断来说，根据矛盾律，可由其中一个为真，推断出另一个为假，但是不能由一个为假来断定另一个为真.然而，根据排中律的原理，我们不但能够由其中一个为真推断出另一个为假，同时也能够由一个为假来推断出另一个为真.反证法的逻辑依据是矛盾律和排中律.在运用反证法来证明问题时，根据推出的矛盾和结果来否定反设，用的就是矛盾律；在否定反设之后，能够肯定原命题的正确性，用的是排中律.反证法解题的一般步骤为：第一步：认真读题，准确找到原命题的条件和结论；第二步：对原命题进行反设，即假设原命题不成立；第三步：由假设出发，进行推理论证，得到与已知条件、公理、定理、公式、定义等相矛盾的结论；第四步：得出最后的结论，证明原命题成立.对于命题：p⇒q，则需先假设命题结论q不成立，即¬q成立，然后由p和¬q出发，运用相关的定理、性质、公式等进行推理，得出相矛盾的结果，断定是结论q成立，从而间接地证明了命题p⇒q为真.反证法的应用范围较广，可用于解答方程、不等式、函数、数列、解析几何、三角函数、立体几何等问题，下面举例说明.例1.求证：方程2x=3有且只有一个根.证明：由2x=3，可得x=log23，则方程2x=3有解.下面运用反证法来证明方程2x=3只存在唯一的赵雪岑。

定积分、曲线积分、重积分、曲面积分的几何意义(2014.1.25)一、定积分x d x f b a ⎰)(1、物理意义：变速直线运动的路程⎰21)(t t dt t v （或变力沿直线做功⎰ba dr r F )(） 2、几何意义：求以)(x f 为曲边的曲边梯形的面积当)(x f =1时，x d ba ⎰表示求直线段的长度二、曲线积分第一型曲线积分(对弧长) (,)L f x y ds ⎰（或(,,)Lf x y z ds ⎰） 1、物理意义 ：求曲线段的质量（()y x f ,表示线密度）2、几何意义：当()时，1,=y x f ()ds y x f l ,⎰表示求曲线段的长度 第二型曲线积分(对坐标)(,)(,)L P x y dx Q x y dy +⎰（或(,,)(,,)(,,)LP x y z dx Q x y z dy R x y z dz ++⎰） 物理意义：求变力做功 三、重积分二重积分(,)D f x y d σ⎰⎰1、物理意义：求平面薄板的质量（()y x f ,表示面密度）（或加在平面面积上压力（压强可变））2、几何意义：求以()y x f z ,=为曲顶的曲顶柱体的体积当()时，1,=y x f σd y x f D ),(⎰⎰表示求平面区域D 的面积 三重积分(,,)V f x y z dV ⎰⎰⎰1、物理意义：求空间物体的质量（),,(z y x f 表示体密度）2、几何意义：当),,(z y x f =1时，⎰⎰⎰VdV 表示求空间区域V 的体积四、曲面积分第一型曲面积分（对面积）(,,)S f x y z dS ⎰⎰1、物理意义：求曲面块的质量（),,(z y x f 表示面密度）2、几何意义：当),,(z y x f =1时，⎰⎰S dS 表示求曲面快的面积 第二型曲面积分（对坐标）(,,)(,,)(,,)S P x y z dydz Q x y z dzdx R x y z dxdy ++⎰⎰物理意义：求流经曲面流体的流量。

定积分小于零的几何意义定积分这个概念啊，就像是一场神秘的数学之旅中的一个奇妙站点。

咱们先不说那些干巴巴的定义，就从几何意义这方面来讲讲定积分小于零的情况。

咱可以把定积分想象成是计算一块图形的面积，不过这个面积有点特殊。

如果定积分小于零呢，这就好比是在一个奇怪的世界里，你看到的不是那种常规的、让人看着就高兴的面积，而是一种“负面积”。

这是啥意思呢？打个比方啊，就像你挖地洞。

你在平地上挖出一个坑，这个坑相对于地面来说，就是一种“负的凸起”。

在数学里的图形上，它就好像是在坐标轴下方的部分。

比如说，咱们有个函数图像，这个图像弯弯绕绕的。

当我们求定积分的时候，如果这个定积分小于零，那就意味着这个函数图像在坐标轴下方所围成的那块区域在“面积计算”里是一种特殊的存在。

它不像在坐标轴上方的部分，坐标轴上方的部分算出来的定积分是正的，就像在地面上盖房子，房子占的那块地的面积就是正的。

可坐标轴下方呢，就像是把地挖走了一块，在面积的概念里，这就是一种“负的贡献”。

你再想想，假如你有个存钱罐，坐标轴上方的定积分就像是往存钱罐里放钱，每一块小的面积就像是一枚枚硬币，让存钱罐越来越满。

而定积分小于零呢，就像是从存钱罐里往外掏钱，存钱罐里的钱越来越少，这就对应着这个特殊的“负面积”在不断地减少整体的数值。

从另一个角度看，定积分小于零也像是欠了债。

在坐标轴上方的部分是你拥有的财产，是正数。

而坐标轴下方，就像是你向别人借了东西，是一种亏欠的状态。

这个亏欠的数值就是定积分小于零的体现。

比如说你借了别人的文具，每一个文具就像是坐标轴下方函数图像所围成的小部分，这些小部分累积起来，就是你总共亏欠的数量，也就是这个小于零的定积分。

在生活里我们可都不希望自己的事情出现“定积分小于零”的情况啊。

就像做生意，如果利润的计算就像求定积分，谁也不想利润是负数吧，那可就意味着亏本了。

这亏本就和定积分小于零是一个道理，你的收入没有你的支出多，就像坐标轴下方的面积超过了坐标轴上方的面积一样。

定积分的几何意义圆定积分是微积分中的一个重要概念，具体描述了一个曲线下方所夹的面积，其数值等于该曲线与x轴之间的有向面积。

在几何学中，定积分有着丰富的几何意义。

其中一个经典的例子就是圆的面积计算。

在解释圆面积的几何意义之前，先简单介绍一下定积分的定义和用法。

定积分的定义是通过极限的思想，将一个曲线下方所夹的区域划分成无穷多个微小的矩形，然后求出这些微小矩形的面积之和。

在数学符号中，定积分可以表示为：∫f(x)dx其中f(x)表示被积函数，dx表示积分变量。

整个符号∫表示积分操作。

在几何学中，我们可以利用定积分来计算一些平面图形的面积。

一般来说，我们将平面图形分解成无穷多个微小的面元，然后对每个微小面元的面积进行积分求和，即可得到整个图形的面积。

以圆的面积计算为例，我们可以采用极坐标的方法来计算。

对于一个原点在圆心的圆，我们可以用角度θ和半径r来表示圆上的每一个点。

根据极坐标系下的坐标变换公式，我们可以得到圆上的任意一点P的坐标（r,θ）。

现在考虑将圆分割成无数个等角度的扇形，并用r和θ的变化范围来描述每个扇形。

由于圆的对称性，每个扇形的面积相等。

我们选取一个扇形，将其与x轴连线，得到一个三角形，其底边长度为r，高度为r*sinθ。

因此一个扇形的面积可以表示为：dA=(1/2)r^2*dθ其中dA表示扇形的面积，dθ表示角度的微小变化。

如果我们将整个圆分割成无数个这样的扇形，并对每个扇形的面积进行积分，那么整个圆的面积可以表示为：A=∫(1/2)r^2dθ在数学上，我们知道圆的周长公式为C = 2πr，所以根据周长和半径的关系，我们可以将dθ表示为ds/r，其中ds表示圆弧的长度。

代入上述公式中，我们可以得到：A = ∫(1/2)r ds在这个公式中，r表示圆的半径，ds表示圆弧的长度。

由于圆弧长度等于圆周长的一部分，因此可以将r表示为2π，并进行替换，得到：A = ∫π ds这个公式的几何意义非常明显，即圆的面积等于圆周长的一部分乘以π。

定积分的几何意义公式
定积分的几何意义
什么是定积分？
定积分是微积分中的重要概念，表示函数曲线下的面积。

它是对连续函数在闭区间上求和的极限，也可以理解为函数曲线与x轴之间的有向面积。

定积分的符号表示
定积分可以用以下公式表示：
b
(x)dx
∫f
a
其中，f(x)是要求积分的函数，a和b是积分的上下限。

定积分的几何意义
定积分的几何意义就是函数曲线与x轴之间的有向面积。

当函数为正值时，定积分表示曲线上方的面积；当函数为负值时，定积分表示曲线下方的面积。

定积分的几何计算
根据定积分的几何意义，我们可以通过计算函数曲线与x轴之间的有向面积来求定积分。

例如，我们要计算函数 f (x )=x 2 在区间 [0,2] 上的定积分，则可以进行如下计算：
∫x 22
0dx =13x 3|02=13(23−03)=83 因此，函数 f (x )=x 2 在区间 [0,2] 上的定积分为 83，表示曲线与x 轴之间的有向面积为 83。

定积分的性质
定积分具有以下性质：
•
积分的线性性质：∫(f (x )+g (x ))b a dx =∫f b a (x )dx +∫g b a
(x )dx •
区间可加性：∫f c a (x )dx =∫f b a (x )dx +∫f c b (x )dx 这些性质使得定积分在实际运用中更加灵活和方便。

总结： - 定积分是表示函数曲线下的有向面积的概念； - 定积
分可以用公式∫f b a
(x )dx 表示； - 定积分的计算可以通过几何方法求出所对应的面积； - 定积分具有线性性质和区间可加性。