机构自由度
- 格式:ppt
- 大小:2.65 MB
- 文档页数:44

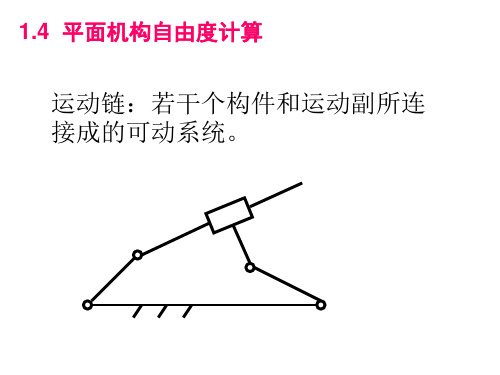
1.4 平面机构自由度计算运动链:若干个构件和运动副所连接成的可动系统。
机构:在运动链中,如果将某一个构件加以固定,而让另一个或几个构件按给定运动规律相对固定构件运动时,如果运动链中其余各活动构件都有确定的相对运动,则此运动链称为机构。
机构是具有确定运动的运动链。
机架原动件从动件在运动链中,将某一个构件加以固定,而让另一个或几个构件按给定运动规律相对固定构件运动时,如果运动链中其余各构件都有确定的相对运动,则此运动链成为机构。
并非任何一个运动链都具有确定的运动可能的情况具有确定的相对运动无相对运动相对运动不确定1.4.1 机构自由度的计算自由度:构件所具有的独立运动的数目,或确定构件位置所需的独立变量的数目自由构件(空间):F = 6自由构件(平面):F = 3约束:运动副对构件独立运动所加的限制自由度数------构件所具有的独立运动的数目称自由度。
A B q 作平面运动的刚体有三个自由度x Ay A (三个坐标参数才能确定其位置)低副的引入减少两个自由度xq高副的引入减少一个自由度沿法线方向不能运动)(xfy机构的自由度数F(需要F 个坐标参数才能确定机构中所有构件的位置)。
L h32F n P P =--活动构件数目低副数目高副数目机构的自由度数F应等于机构的原动件数hl 23P P n F --=活动构件数目低副数目高副数目1.4.2 机构具有确定运动的条件:运动链中取一个构件相对固定作为机架,运动链相对于机架的自由度必须大于零,且原动件数目等于运动链自由度数。
满足此条件的运动链即成为机构,机构自由度的计算可采用运动链自由度的计算公式。
“机构”的定义:在运动链中,将某一个构件加以固定,而让另一个或几个构件按给定运动规律相对固定构件运动时,如果运动链中其余各构件都有确定的相对运动,则此运动链成为机构。
qq2 qq3q2 qq运动链成为机构的条件运动链的自由度F= ?运动链的运动情况如何?F= 3×4 -2×5 = 21 个原动件> 0,但原动件数目小于自由度数目,运动链运动不确定,不能成为机构。




机械原理机构自由度计算要计算机械原理机构的自由度,首先需要确定机构中的连杆和连接关系。
连杆是构成机构的杆件,连接关系是将连杆连接在一起的方式。
机构中的连杆可以是刚性的或柔性的,连接关系可以通过铰链、滑动副或传动副来实现。
在计算自由度时,通常会假设连杆是刚性的,以简化计算。
计算机械原理机构的自由度时,有两种常见的方法可供选择:迭代法和非迭代法。
在迭代法中,我们首先假设机构的自由度为零,并逐步增加约束,直到无法增加为止。
每次增加约束时,我们需要检查相应的自由度是否减少。
如果自由度减少,则保留该约束;如果自由度没有减少,则将该约束排除。
通过迭代这一过程,我们最终可以得到机构的自由度。
相比之下,非迭代法更为直接。
我们可以根据机构中的约束条件和自由关系,直接计算出机构的自由度。
这种方法在约束较少或机构较简单的情况下尤其适用。
无论使用哪种方法,计算机械原理机构的自由度都需要考虑以下几个因素:1.连杆的数量:连杆的数量对机构的自由度有直接影响。
一个机构中的连杆数量越多,其自由度也就越高。
2.连杆的长度:连杆的长度决定了机构的运动幅度。
较长的连杆通常会增加机构的自由度。
3.连接关系:不同的连接关系会导致机构自由度的不同。
例如,一个通过滑动副连接的机构可能具有比通过传动副连接的机构更大的自由度。
通过对上述因素进行综合考虑,我们可以计算出机械原理机构的自由度,并据此来分析和优化机构的设计。
机构的自由度不仅与其运动性能和稳定性有关,还与动力学和控制系统的设计密切相关。
总结起来,机械原理机构的自由度计算是理解和设计复杂机构的重要步骤之一、通过迭代法或非迭代法,我们可以计算出机构的自由度,并据此分析和优化机构的性能。
在进行自由度计算时,我们需要考虑连杆的数量、长度和连接关系等因素。
这些计算为机构的设计和应用提供了理论依据。
机构自由度的概念
机构自由度(Degree of Freedom, DoF)是机械原理中的一个核心概念,它描述了一个机构在没有外力或驱动力作用下能够独立完成的运动的数量。
具体来说:
机构自由度定义:
在一个机械机构中,为了确定该机构所有构件的相对位置和姿态,所需要的独立运动参数的数量称为机构的自由度。
- 对于单个构件而言,在三维空间中,它有6个自由度,包括沿三个正交方向(X、Y、Z轴)的平动自由度以及绕这三个轴的转动自由度。
- 当多个构件通过运动副(如铰链、滑块等)相互连接组成机构时,由于运动副对构件的约束作用,实际的机构自由度会小于各个独立构件自由度之和。
- 机构的总自由度计算公式为:总自由度= 各构件自由度之和- 约束数(即由运动副引入的约束数目)。
- 在实际应用中,如果机构具有一个或多个原动件(例如电机、气缸等驱动部件),并且原动件提供的独立输入变量与机构自由度相
匹配,则机构可以实现确定的、预设的运动。
平面机构自由度通常指机构在二维平面内的自由度,一般包括沿两个正交方向的移动自由度及一个绕垂直于平面轴的转动自由度。
总结来说,机构自由度是评价机构运动特性的重要指标,对于设计和分析机械设备有着至关重要的意义。
只有当机构的自由度等于零时,机构才是完全刚性固定的结构;而具有至少一个自由度的机构才能够产生相对运动,并可能成为有用的机械装置。