人工神经网络复习资料
- 格式：docx
- 大小：4.03 MB
- 文档页数：36
下载文档原格式
合集下载
D人工神经网络复习习题
oj
2.2.2 神经元的数学模型(1/6)
我们用一个数学表达式对上述内容可进行抽象与 概括。 令xi(t)表示t时刻神经元j接收的来自神经元i的信 息输入，oj(t)表示t时刻神经元的信息输出，则神经元j 的状态可表达为
n o j (t ) f w ijx i (t ij ) Tj i 1
x1 … xi … xn
w1j wij wnj
j
∑
2.2.1 神经元的建摸(6/6) 人工神经元的输出也同生物神经元一样仅有一个，如用 oj表示神经元j输出。 输出与输入之间的对应关系可用某种函数来表示，这种 函数称为转移函数，一般都是非线性的。
x1 … xi … xn
w1j wij wnj
j
∑
f
第4章 竞争学习神经网络 § 4.1 竞争学习的概念与原理 § 4.1.1 基本概念 § 4.1.2 竞争学习原理 § 4.2 自组织特征映射神经网络 § 4.2.1 SOM网络的生物学基础 § 4.2.2 SOM网(络)的拓扑结构与权值调整域 § 4.2.3 自组织特征映射网(络)的运行原理与学习算法 § 4.2.3.1 运行原理 § 4.2.3.2 学习算法 § 4.2.3.3 功能分析 § 4.3 自组织特征映射网络的设计与应用 § 4.4 自适应共振理论 本章小结
第6章 反馈神经网络 § 6.1 离散型Hopfield神经网络(DHNN) § 6.1.1 网络的结构与工作方式 § 6.1.2 网络的稳定性与吸引子 § 6.1.2.1 网络的稳定性 § 6.1.2.2 吸引子与能量函数 § 6.1.2.3 吸引子的性质 § 6.1.2.4 吸引子的吸引域 § 6.1.3 网络的权值设计 § 6.1.4 网络的信息存储容量 § 6.2 连续型Hopfield神经网络(CHNN) § 6.3 Hopfield网络应用与设计实例 § 6.4 双向联想记忆(BAM)神经网络 § 6.5 随机神经网络 § 6.6 递归神经网络 本章小结
人工神经网络第章(1)
人工神经网络第章(1)人工神经网络第章人工神经网络（Artificial Neural Networks，ANN）是一种受到生物神经系统启发而开发出来的计算模型，在机器学习、数据挖掘、自然语言处理等领域广泛应用。
在本章节中，我们将对人工神经网络的基本原理、训练方法和应用进行介绍。
一、基本原理人工神经网络是由多个神经元（Neuron）组成的网络。
每个神经元接收多个输入信号，经过一些加权处理后，产生一个输出信号，输出信号又作为下一层神经元的输入。
这种层层叠加的结构被称为前馈神经网络（Feedforward neural networks）。
每个神经元的输入信号通过一个激活函数（Activation function）进行非线性转换，得到神经元的输出。
常用的激活函数有sigmoid、ReLU、tanh等。
神经网络的输出可以用于分类、回归等任务。
二、训练方法神经网络训练的目标是调整神经元之间的权值，使得网络的输出接近于真实值。
常用的训练方法包括反向传播算法（Backpropagation）和随机梯度下降算法（Stochastic Gradient Descent）。
反向传播算法是目前使用最广泛的神经网络训练方法，其核心思想是“误差反向传播”。
即从输出层开始，将网络的输出误差逐层反向传播到输入层，计算每个神经元的误差贡献，最后通过梯度下降算法调整神经元权值。
随机梯度下降算法是一种在线学习算法，每次选择一个样本进行训练，通过计算损失函数的梯度方向，调整网络权值，直到收敛。
随机梯度下降算法能够处理大规模数据训练，但更容易陷入局部极小值。
三、应用领域人工神经网络在图像识别、语音识别、自然语言处理、机器翻译等领域取得了广泛应用。
在图像识别领域，卷积神经网络（CNN）被广泛应用，已经实现了在ImageNet等数据集上的超越人类表现的成果。
在自然语言处理领域，循环神经网络（RNN）和长短时记忆网络（LSTM）能够处理变长序列数据，已经成功应用于机器翻译、情感分析等任务。
第一讲 人工神经网络的基本知识
1.3.2 人工神经元模型
1.3.2 人工神经元模型
一组连接（对应于生物神经元的突触），连接 强度由各连接上的权值表示，权值为正表示激 活，为负表示抑制。 一个求和单元，用于求取各输入信号的加权和 （线性组合). 一个非线性激活函数(作用函数)，起非线性映 射作用并将神经元拘出幅度限制在一定范围内.
课程目的和基本要求
了解人工神经网络的有关研究思想，从中 学习开拓者们的部分问题求解方法。 通过实验进一步体会有关模型的用法和性 能，获取一些初步的经验。 查阅适当的参考文献，将所学的知识与自 己未来研究课题（包括研究生论文阶段的 研究课题）相结合起来，达到既丰富学习 内容，又有一定的研究和应用的目的。
1、控制输入对输出的激活作用； 2、对输入、输出进行函数转换； 3、将可能无限域的输入变换成指定的有 限范围内的输出。
几种常用的作用函数
1、阈值函数．
M-P 模型
几种常用的作用函数
2，分段线性函数
它类似于一个放大系数为1 的非线性放大器，当工作 于线性区时它是一个线性 组合器，放大系数趋于无 穷大时变成一个阈值单元。
1、构成
2、工作过程：树突
轴突
突触 其他神经元
1.3.1 生物神经网
3、六个基本特征：
1）神经元及其联接； 2）神经元之间的联接强度决定信号传递的强弱； 3）神经元之间的联接强度是可以随训练改变的； 4 ）信号可以是起 刺激 作用的，也可以是起 抑制 作用 的； 5 ）一个神经元接受的信号的 累积效果 决定该神经元 的状态； 6)每个神经元可以有一个“阈值”。
第二高潮期（1983~1990） 1982年，J. Hopfield提出循环网络，并 将Lyapunov函数作为网络性能判定的 能量函数，阐明了人工神经网络与动力 学的关系，用非线性动力学的方法来研 究人工神经网络的特性，建立了人工神 经网络稳定性的判别依据，指出信息被 存放在网络中神经元的联接上。
D人工神经网络复习习题
对模拟神经元的每一个输入都有一个加权系数wij，称为权 重值，其正负模拟了生物神经元中突触的兴奋和抑制，其大小 则代表了突触的不同连接强度。
x1 w1j
… xi
wij
j
… wnj
xn
2.2.1 神经元的建摸(5/6)
作为基本处理单元，必须对全部输入信号进行整合，以确 定各类输入的作用总效果，组合表示输入信号的“总和值”， 相应于生物神经元的膜电位。
第4章 竞争学习神经网络 § 4.1 竞争学习的概念与原理
§ 4.1.1 基本概念 § 4.1.2 竞争学习原理 § 4.2 自组织特征映射神经网络 § 4.2.1 SOM网络的生物学基础 § 4.2.2 SOM网(络)的拓扑结构与权值调整域 § 4.2.3 自组织特征映射网(络)的运行原理与学习算法
2.2.2 神经元的数学模型(3/6)
n
o j(t 1 ) f w ix ji(t) T j
i 1
(2 .2 )
输入总和常称为神经元在t时刻的净输入，用
n
n'j( e t) t w ix ji(t)
(2 .3 )
i 1
当net’j>Tj时，神经元j才能被激活。
oj(t+1)与xi(t)之间的单位时间差代表所有神经 元具有相同的、恒定的工作节律，wij与时间无关。
§ 2.2 人工神经元模型
人工神经网络是在现代神经生物学研究基础上提出的模 拟生物过程以反映人脑某些特性的计算结构。它不是人脑神 经系统的真实描写，而只是人脑神经系统的某种抽象、简化 和模拟。
神经元及其突触是神经网络的基本器件。因此，模拟生 物神经网络应首先模拟生物神经元。
在人工神经网络中，神经元常被称为“处理单元”。 人工神经元是对生物神经元的一种形式化描述； 人工神经元是对生物神经元的信息处理过程进行抽象， 并用数学语言予以描述； 人工神经元是对生物神经元的结构和功能进行模拟，并 用模型图予以表达。
x1 w1j
… xi
wij
j
… wnj
xn
2.2.1 神经元的建摸(5/6)
作为基本处理单元，必须对全部输入信号进行整合，以确 定各类输入的作用总效果，组合表示输入信号的“总和值”， 相应于生物神经元的膜电位。
第4章 竞争学习神经网络 § 4.1 竞争学习的概念与原理
§ 4.1.1 基本概念 § 4.1.2 竞争学习原理 § 4.2 自组织特征映射神经网络 § 4.2.1 SOM网络的生物学基础 § 4.2.2 SOM网(络)的拓扑结构与权值调整域 § 4.2.3 自组织特征映射网(络)的运行原理与学习算法
2.2.2 神经元的数学模型(3/6)
n
o j(t 1 ) f w ix ji(t) T j
i 1
(2 .2 )
输入总和常称为神经元在t时刻的净输入，用
n
n'j( e t) t w ix ji(t)
(2 .3 )
i 1
当net’j>Tj时，神经元j才能被激活。
oj(t+1)与xi(t)之间的单位时间差代表所有神经 元具有相同的、恒定的工作节律，wij与时间无关。
§ 2.2 人工神经元模型
人工神经网络是在现代神经生物学研究基础上提出的模 拟生物过程以反映人脑某些特性的计算结构。它不是人脑神 经系统的真实描写，而只是人脑神经系统的某种抽象、简化 和模拟。
神经元及其突触是神经网络的基本器件。因此，模拟生 物神经网络应首先模拟生物神经元。
在人工神经网络中，神经元常被称为“处理单元”。 人工神经元是对生物神经元的一种形式化描述； 人工神经元是对生物神经元的信息处理过程进行抽象， 并用数学语言予以描述； 人工神经元是对生物神经元的结构和功能进行模拟，并 用模型图予以表达。
人工神经网络基础知识
x0 x0
• MP模型
可知当神经元i的输入信号加权和超过阈值时，输出为
“1”，即“兴奋”状态；反之输出为“0”，是“抑制” 状态。
激发函数的基本作用
– 控制输入对输出的激活作用 – 对输入、输出进行函数转换 – 将可能无限域的输入变换成指定的有限范围内的输出
例、实现逻辑函数“与门”（AND gate）运 算。
2 人工神经网络基础知识
2.1人工神经网络的生物学基础
人的智能来自于大脑，大脑是由大量的神经细胞或神经元 组成的。每个神经元可以看作为一个小的处理单元，这些神经 元按照某种方式互相连接起来，构成了大脑内部的生物神经元 网络，他们中各神经元之间连接的强弱，按照外部的激励信号 作自适应变化，而每个神经元又随着接收到的多个激励信号的 综合大小呈现兴奋或抑制状态。据现在的了解，大脑的学习过 程就是神经元之间连接强度随外部激励信息做自适应变化的过 程，大脑处理信息的结果确由神经元的状态表现出来。显然， 神经元是信息处理系统的最小单元。虽然神经元的类型有很多 种，但其基本结构相似。
（1）每个神经元都是一个多输入单输出的信息处理单元； （2）突触分兴奋性和抑制性两种类型； （3）神经元具有空间整合特性和阈值特性； （4）神经元输入输出间有固定的时滞，主要取决于突触延搁； （5）忽略时间整合作用和不应期； （6）神经元本身是非时变的，即其突触时延和突触强度均为常 数。
MP模型：
1
x 1ex
f(x) (1t 2
h2)1ex
f(x) 1.0
o
x
-1.0
图
双极 性 S型函数
3、线性函数 （1）线性作用函数：输出等于输入，即 yf(x)x
（2）饱和线性作用函数 （3）对称饱和线性作用函数
人工神经网络1资料
6/17/2019
1.2.3 处理和计算能力
• NNs具有巨量信息并行处理和大规模平行 计算能力
–每个神经元对所接受的信息作相对独立的处 理，但各个神经元之间可以并行、协同地工 作
– 人脑每个神经元很简单，但由于大脑总计形 成10E14-15个突触，使得人脑1s内可完成 计算机至少需要10亿处理步骤才能完成的任 务。
6/17/2019
1.1 人工神经网络的提出
• 1.1.3 联接主义观点 • 核心：智能的本质是联接机制。 • 神经网络是一个由大量简单的处理单元组
成的高度复杂的大规模非线性自适应系统 • ANN力求从四个方面去模拟人脑的智能行为
–物理结构 –计算模拟 –存储与操作 –训练
6/17/2019
1.1 人工神经网络的提出
6/17/2019
• 擅长两个方面：
–对大量的数据进行分类，并且只有较少的几种 情况；
–必人们主要将其用于语音、视觉、知识处理、辅 助决策等方面。
–在数据压缩、模式匹配、系统建模、模糊控制、 求组合优化问题的最佳解的近似解（不是最佳 近似解）等方面也有较好的应用。
6/17/2019
1.2 人工神经网络的概念
（2）Simpson：人工神经网络是一个非 线性的有向图，图中含有可以通过改 变权大小来存放模式的加权边，并且 可以从不完整的或未知的输入找到模 式。
非线性的有向图 加权边、存放模式 不完整、未知输入的处理
6/17/2019
1.2 人工神经网络的概念
• 1.1.1 物理符号系统 •
人脑的反映 形式化
现实
信息
数据
物理系统
物理符号系统 表现智能
6/17/2019
1.1 人工神经网络的提出
1.2.3 处理和计算能力
• NNs具有巨量信息并行处理和大规模平行 计算能力
–每个神经元对所接受的信息作相对独立的处 理，但各个神经元之间可以并行、协同地工 作
– 人脑每个神经元很简单，但由于大脑总计形 成10E14-15个突触，使得人脑1s内可完成 计算机至少需要10亿处理步骤才能完成的任 务。
6/17/2019
1.1 人工神经网络的提出
• 1.1.3 联接主义观点 • 核心：智能的本质是联接机制。 • 神经网络是一个由大量简单的处理单元组
成的高度复杂的大规模非线性自适应系统 • ANN力求从四个方面去模拟人脑的智能行为
–物理结构 –计算模拟 –存储与操作 –训练
6/17/2019
1.1 人工神经网络的提出
6/17/2019
• 擅长两个方面：
–对大量的数据进行分类，并且只有较少的几种 情况；
–必人们主要将其用于语音、视觉、知识处理、辅 助决策等方面。
–在数据压缩、模式匹配、系统建模、模糊控制、 求组合优化问题的最佳解的近似解（不是最佳 近似解）等方面也有较好的应用。
6/17/2019
1.2 人工神经网络的概念
（2）Simpson：人工神经网络是一个非 线性的有向图，图中含有可以通过改 变权大小来存放模式的加权边，并且 可以从不完整的或未知的输入找到模 式。
非线性的有向图 加权边、存放模式 不完整、未知输入的处理
6/17/2019
1.2 人工神经网络的概念
• 1.1.1 物理符号系统 •
人脑的反映 形式化
现实
信息
数据
物理系统
物理符号系统 表现智能
6/17/2019
1.1 人工神经网络的提出
第四章人工神经网络讲义
2019/2/15 7
4.1 概述——人工神经网络研究与发展
1986年Rumelhart等人在多层神经网络模型的基础上，提出了 多层神经网络模型的反向传播学习算法(BP算法)，解决了多层 前向神经网络的学习问题，证明了多层神经网络具有很强的学 习能力，它可以完成许多学习任务，解决许多实际问题。 近十几年来，许多具备不同信息处理能力的神经网络已被提出 来并应用于许多信息处理领域，如模式识别、自动控制、信号 处理、决策辅助、人工智能等方面。 神经计算机的研究也为神经网络的理论研究提供了许多有利条 件，各种神经网络模拟软件包、神经网络芯片及电子神经计算 机的出现，体现了神经网络领域的各项研究均取得长足进展。 同时，相应的神经网络学术会议和神经网络学术刊物的大量出 现，给神经网络的研究者们提供了许多讨论交流的机会。
第 四 章
人工神经网络
2019/2/15
1
4.1 概述
2019/2/15
2
4.1 概述——人工神经网络研究与发展
人工神经网络(简称神经网络)是利用物理器件来模拟生物神经网 络的某些结构和功能。 40年代初，美国Mc Culloch和Pitts从信息处理的角度，研究神 经细胞行为的数学模型表达，并提出了二值神经元模型。
2019/2/15 9
4.1 概述—人脑信息处理机制
生物神经系统，包括中枢神经系统和大脑，均是由各类神经元 组成。 其独立性是指每一个神经元均有自己的核和自己的分界线或原 生质膜。 生物神经元之间的相互连接从而让信息传递的部位被称为突触 (Synapse) 。突触按其传递信息的不同机制，可分为化学突触和 电突触。其中化学突触占大多数，其神经冲动传递借助于化学 递质的作用。 生物神经元的结构大致描述如下图所示。
2019/2/15 8
4.1 概述——人工神经网络研究与发展
1986年Rumelhart等人在多层神经网络模型的基础上，提出了 多层神经网络模型的反向传播学习算法(BP算法)，解决了多层 前向神经网络的学习问题，证明了多层神经网络具有很强的学 习能力，它可以完成许多学习任务，解决许多实际问题。 近十几年来，许多具备不同信息处理能力的神经网络已被提出 来并应用于许多信息处理领域，如模式识别、自动控制、信号 处理、决策辅助、人工智能等方面。 神经计算机的研究也为神经网络的理论研究提供了许多有利条 件，各种神经网络模拟软件包、神经网络芯片及电子神经计算 机的出现，体现了神经网络领域的各项研究均取得长足进展。 同时，相应的神经网络学术会议和神经网络学术刊物的大量出 现，给神经网络的研究者们提供了许多讨论交流的机会。
第 四 章
人工神经网络
2019/2/15
1
4.1 概述
2019/2/15
2
4.1 概述——人工神经网络研究与发展
人工神经网络(简称神经网络)是利用物理器件来模拟生物神经网 络的某些结构和功能。 40年代初，美国Mc Culloch和Pitts从信息处理的角度，研究神 经细胞行为的数学模型表达，并提出了二值神经元模型。
2019/2/15 9
4.1 概述—人脑信息处理机制
生物神经系统，包括中枢神经系统和大脑，均是由各类神经元 组成。 其独立性是指每一个神经元均有自己的核和自己的分界线或原 生质膜。 生物神经元之间的相互连接从而让信息传递的部位被称为突触 (Synapse) 。突触按其传递信息的不同机制，可分为化学突触和 电突触。其中化学突触占大多数，其神经冲动传递借助于化学 递质的作用。 生物神经元的结构大致描述如下图所示。
2019/2/15 8
人工神经网络复习资料
learning algorithm
training examples
input vector
Target output
desired response
supervised learning
Unsupervised Learning
learning tasks
rate of learning
生物神经元
人工神经元神经元
输出神经元
互联加权
偏见水平
激活功能
前馈神经网络
隐藏的图层
输出层
输入输出映射
关联记忆
模式识别
系统识别
感知器模型
学习过程
学习算法
训练实例
输入矢量
目标输出
期望的响应
监督学习
无监督学习
学习任务
学习的速度
2.
3.
3.
3.
3.
4．
算法实现步骤：
第一步:初始化
第二步：输入一个样本，计算连接权值的调整量
feedforward neural network
hidden layers
output layer
input-output mapping
Association memory
Pattern Recognition
system identification
perceptron model
Learning Processes
10,。Apபைடு நூலகம்lications of RBF network
4.
5.
6.When no node节点output is an input to a node in the same layer or preceding layer前层, the network is a feedforward network(前向网络).
training examples
input vector
Target output
desired response
supervised learning
Unsupervised Learning
learning tasks
rate of learning
生物神经元
人工神经元神经元
输出神经元
互联加权
偏见水平
激活功能
前馈神经网络
隐藏的图层
输出层
输入输出映射
关联记忆
模式识别
系统识别
感知器模型
学习过程
学习算法
训练实例
输入矢量
目标输出
期望的响应
监督学习
无监督学习
学习任务
学习的速度
2.
3.
3.
3.
3.
4．
算法实现步骤：
第一步:初始化
第二步：输入一个样本，计算连接权值的调整量
feedforward neural network
hidden layers
output layer
input-output mapping
Association memory
Pattern Recognition
system identification
perceptron model
Learning Processes
10,。Apபைடு நூலகம்lications of RBF network
4.
5.
6.When no node节点output is an input to a node in the same layer or preceding layer前层, the network is a feedforward network(前向网络).
人工神经网络概述
参考内容二
人工神经网络（Artificial Neural Network，简称ANN）是一种模拟人类 神经系统运作的数学模型，由多个简单计算单元（即神经元）组成，通过学习方 式从数据中提取模式并预测未来数据。
一、人工神经网络的基本结构
人工神经网络的基本结构包括输入层、隐藏层和输出层。输入层负责接收外 部输入的数据，隐藏层通过一系列复杂的计算将输入转化为有意义的特征，最后 输出层将隐藏层的结果转化为具体的输出。在隐藏层中，每个神经元都通过权重 和激活函数来对输入进行转换，以产生更有意义的输出。
根据任务的不同，人工神经网络可以分为监督学习、无监督学习和强化学习 三种。监督学习是指通过输入输出对之间的映射关系来训练模型；无监督学习是 指通过聚类或降维等方式来发现数据中的潜在规律；强化学习是指通过与环境的 交互来学习策略，以达到在给定的情况下采取最优行动的目标。
四、人工神经网络的未来发展
随着深度学习技术的不断发展，人工神经网络的性能和应用范围也在不断扩 大。未来的人工神经网络将更加注重模型的可解释性和鲁棒性，同时也将更加注 重跨领域的研究和应用。此外，随着计算机硬件的不断升级和算法的不断优化， 人工神经网络的训练速度和精度也将不断提高。
三、人工神经网络的种类
根据连接方式的不同，人工神经网络可以分为前馈神经网络和反馈神经网络 两种。前馈神经网络是一种层次结构，其中每个节点只与前一层的节点相连，每 个节点的输出都是前一层的加权输入。而反馈神经网络则是一种循环结构，其中 每个节点都与前一层的节点和后一层的节点相连，每个节点的输出不仅取决于前 一层的输入，还取决于后一层的输出。
反向传播算法是一种监督学习算法，它通过比较网络的输出和真实值来计算 误差，然后将这个误差反向传播到网络中，调整每个神经元的权重以减小误差。
人工神经网络(网络资料)
人工神经网络1、基本特征(1)结构特征 并行处理（时间）、分布式存储（空间）与容错性(2)能力特征 自适应性（自学习和自组织）2、基本功能(1)联想记忆 自联想和异联想(2)非线性映射(3)分类与识别(4)优化计算(5)知识处理3、神经元建模：(1)每个神经元都是一个多输入单输出的信息处理单元；(2)神经元输入分兴奋性输入和抑制性输入两种类型；(3)神经元具有空间整合性和阈值特性；(4)神经元输入与输出间有固定的时滞，主要取决于突触延搁；(5)忽略时间整合作用和不应期；(6)神经元本身是非时变的，即其突触时延和突触强度均为常数。
4、人工神经元模型令)(t x i 表示t 时刻神经元j 接收的来自神经元i 的输入信息，)(t o j 表示t 时刻神经元j 的输出信息，则神经元j 的状态可表达为：})]({[)(1∑=--=ni j ij i ij j T t x w f t o τ其中，ij τ为输入输出间的突触时延，j T 为神经元j 的阈值，ij w 为神经元i 到j 的突触连接系数或称权重值，()∙f 为神经元转移函数。
取1=ij τ，则有：})]({[)1(1∑=-=+ni j i ij j T t x w f t o输入总和常称为神经元在t 时刻的净输入，用下式表示：∑=='ni i ij j t x w t t ne 1)()()(t t ne j '体现了神经元j 的空间整合性，而未考虑时间整合，当0)(>-'j j T t t ne 时，神经元才能被激活。
上式还可表示为权重向量j W 和输入向量X 的点积：X W t ne T j j ='其中j W 和X 均为列向量，定义为：T nj j j j w w w W ),,,(21 =T n x x x X ),,,(21 =如果令10-=x ，j j T w =0，则有j j w x T 00=-，因此净输入与阈值之差可表达为：∑====-'ni T j i ij j j j X W x w net T t ne 0综合以上各式，神经元模型可简化为：)()(X W f net f o T j j j ==5、神经元的转移函数(1)阈值型转移函数(M-P 模型) 处理离散信号单极性阈值型转移函数 单位阶跃函数双极性阈值型转移函数 sgn(x)(2)非线性转移函数（单极性/双极性Sigmoid 函数曲线）实数域R 到[0,1]闭集的非减性连续函数，代表了状态连续型神经元模型。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
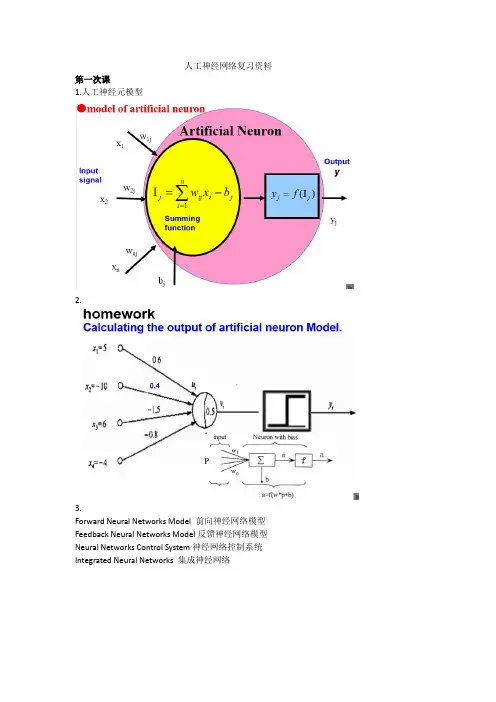
人工神经网络复习资料第一次课1.人工神经元模型2.3.Forward Neural Networks Model前向神经网络模型Feedback Neural Networks Model反馈神经网络模型Neural Networks Control System神经网络控制系统Integrated Neural Networks集成神经网络4.5.6.When no node节点output is an input to a node in the same layer or preceding layer前层, the network is a feedforward network(前向网络).当输出被引导为输入到相同的或之前的层节点时，网络是反馈网络 反馈网络,封闭的循环称为复发性网络(递归网络)7.8.n123n9.神经网络的用途是1分类2模式识别、特征提取、图像匹配3降噪4预测4.感知器（前向网络）5.感知器是一个具有单层计算神经元的神经网络，并由线性阈值元件组成，是最简单的前向网络。
感知器模型是美国学者罗森勃拉特（Rosenblatt）为研究大脑的存储、学习和认知过程而提出的一类具有自学习能力的神经网络模型，Rosenblatt提出的感知器模型是一个只有单层计算单元的前向神经网络，称为单层感知器。
它主要用于模式分类，单层的感知器网络结构如下图所示。
5.感知器算法1）随机地给定一组连接权2）输入一组样本和期望的输出3）计算感知器实际输出4）修正权值5）选取另外一组样本，重复上述2）～4）的过程，直到权值对一切样本均稳定不变为止，学习过程结束。
5. Perceptron Learning Rule该学习算法收敛的充分必要条件是输入样本是线性可分的。
同时的选取也是十分关键的。
学习率选取太小，学习太慢；学习率太大，学习过程可能出现修正过头的情况，从而产生振荡。
5.感知器训练规则及计算方法的掌握5.感知器网络应用利用感知器神经网络架构解决一个简单的模式识别问题。
使用感知器神经网络架构来表示和门1）分类：训练网络预测心脏病新病人2）逻辑运算：单层感知器可以表示和，或者，不，等等，但不是XOR3）6. MATLAB functions for perceptron networks5.应用实例:设计一单层单输出感知器神经网络，进行二值化图像卡片上数字的奇偶分类5.第二次课1．Key wordsbiological neuronArtificial Neural neuron output neurons interconnection weighted bias levelsactivation function feedforward neural network hidden layersoutput layerinput-output mapping Association memory Pattern Recognition system identification perceptron model Learning Processes learning algorithm training examplesinput vectorTarget outputdesired response supervised learning Unsupervised Learninglearning tasks rate of learning 生物神经元人工神经元神经元输出神经元互联加权偏见水平激活功能前馈神经网络隐藏的图层输出层输入输出映射关联记忆模式识别系统识别感知器模型学习过程学习算法训练实例输入矢量目标输出期望的响应监督学习无监督学习学习任务学习的速度2.3.3.3.3.4．算法实现步骤：第一步:初始化第二步：输入一个样本，计算连接权值的调整量第三步：调整连接权值第四步：计算均方误差5．6．线性神经网络的应用线性神经网络在模式识别、信号滤波和预测、函数近似等方面有广泛的用途,至今仍然广泛应用于各种实际系统中,特别是在自适应滤波方面,用途更为广泛。
1以自适应线性网络实现噪声对消2胎儿心率的检测3电话中的回音对消第三次课1．BP网络具有一层或多层隐含层，除了在多层网络上与前面已介绍过的感知器模型有不同外，其主要差别也表现在激活函数上。
感知器是二值型的函数。
BP网络的激活函数必须是处处可微的，所以它就不能采用二值型的阀值函数{0，1}或符号函数{-1，1}，BP网络经常使用的是S型的对数或正切激活函数和线性函数。
用了“BP算法”进行训练的“多层感知器模型3.3.3.3.2.BP网络主要用于（1）Functions approximation：BP can be applied to learn non-linear functions（2）pattern recognition模式识别3.第四次课1.2.径向基函数(RBF-Radial Basis Function)神经网络是由J.Moody和C.Darken 在80年代末提出的一种神经网络,它是具有单隐层的三层前馈网络。
3.3.3.5.6.7.Learning Algorithm如何确定RBF网络隐层节点的中心及基宽度参数是一个困难的问题8.学习算法需要求解的参数1)径向基函数的中心2)方差3)隐含层到输出层的权值学习方法分类（按RBF中心选取方法的不同分）1)随机选取中心法2)自组织选取中心法3)有监督选取中心法4)正交最小二乘法等.自组织选取中心法:第一步，自组织学习阶段无导师学习过程，求解隐含层基函数的中心与方差；第二步，有导师学习阶段求解隐含层到输出层之间的权值。
9.无导师学习阶段，对所有样本的输入进行聚类，求得各隐层节点的RBF的中心ci。
如用k均值聚类算法，调整中心，算法步骤为：（1）给定各隐节点的初始中心；（2）计算距离（欧氏距离）并求出最小距离的节点（3）调整中心（4）计算节点的距离（5）重新调整聚类中心(6).求解方差有导师学习阶段:计算隐含层和输出层之间的权值10,。
Applications of RBF networkFunction Approximation:ClassificationPattern recognition, information process, image process system modelingFailure diagnosisRBF 神经网络结构简单、训练简洁且学习收敛速度快，因此被广泛引用于时间序列分析、模式识别、非线性控制和图像处理等领域。
11.12.13.（1）从网络结构上看。
BP神经网络实行权连接，而RBF神经网络输入层到隐层单元之间为直接连接，隐层到输出层实行权连接。
BP神经网络隐层单元的转移函数一般选择非线性函数（如反正切函数），RBF神经网络隐层单元的转移函数是关于中心对称的RBF（如高斯函数）。
BP神经网络是三层或三层以上的静态前馈神经网络，其隐层和隐层节点数不容易确定，没有普遍适用的规律可循，一旦网络的结构确定下来，在训练阶段网络结构将不再变化；RBF神经网络是三层静态前馈神经网络，隐层单元数也就是网络的结构可以根据研究的具体问题，在训练阶段自适应地调整，这样网络的适用性就更好了.（2）从训练算法上看。
BP神经网络需要确定的参数是连接权值和阈值，主要的训练算法为BP算法和改进的BP算法。
但BP算法易限于局部极小值，学习过程收敛速度慢，隐层和隐层节点数难以确定；RBF神经网络的训练算法支持在线和离线训练，可以动态确定网络结构和隐层单元的数据中心和扩展常数，学习速度快，比BP算法表现出更好的性能。
总之，RBF神经网络可以根据具体问题确定相应的网络拓扑结构，具有自学习、自组织、自适应功能，学习速度快，可以进行大范围的数据融合，可以并行高速地处理数据。
RBF神经网络的优良特性使得其显示出比BP神经网络更强的生命力，正在越来越多的领域内替代BP神经网络。
目前，RBF神经网络已经成功地用于非线性函数、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等.第六次课1.2.竞争学习的概念与原理竞争学习是自组织网络中最常用的一种学习策略，首先说明与之相关的几个基本概念。
1 ）模式、分类、聚类与相似性模式：一般当网络涉及识别、分类问题时，常用输入模式（而不称输入样本）；分类：将待识别的输入模式划分为各自的模式类中去；聚类：无导师指导的分类称为聚类，聚类的目的是将相似的模式样本划归一类；相似性：输入模式的聚类依据。
2）相似性测量神经网络的输入模式用向量表示，比较不同模式的相似性可转化为比较两个向量的距离，因而可用模式向量间的距离作为聚类判据。
模式识别中常用到的两种聚类判据是欧式最小距离法和余弦法。
3.自组织竞争网络机理：采用无教师学习方式，无须期望输出，只是根据数据样本进行学习，并调整自身的权重以达到学习目的。
自组织神经网络的学习规则大都采用竞争型的学习规则。
竞争型神经网络的基本思想是网络竞争层的各神经元通过竞争来获取对输入模式的响应机会，最后仅有一个神经元成为胜利者，并将与获胜神经元有关的各连接权值向着更有利于其竞争的方向调整。
用途：模式分类和模式识别。
4.竞争学习规则——Winner-Take-All网络的输出神经元之间相互竞争以求被激活，结果在每一时刻只有一个输出神经元被激活。
这个被激活的神经元称为竞争获胜神经元，而其它神经元的状态被抑制，故称为Winner Take All。
5.竞争学习规则——Winner-Take-All1）向量归一化2）寻找获胜神经元3)网络输出与权值调整6. SOM网络共有两层，输入层模拟感知外界输入信息的视网膜。
输出层模拟做出响应的大脑皮层。
输出层也是竞争层，网络拓扑结构形式常见有一维线阵和二维平面阵。
7.8. SOM网的学习算法（1）初始化（2）接受输入（3）寻找获胜节点（4）定义优胜邻域(5)调整权值（6）检查总模式数是否全部参与了学习（7）更新邻域Nj*(t)及学习率η(t) (8)结束检查学习率是否衰减到零或某个预定的正小数.9. SOM设计输出层设计输出层神经元数量设定和训练集样本的类别数相关，但是实际中我们往往不能清除地知道有多少类。
如果神经元节点数少于类别数，则不足以区分全部模式，训练的结果势必将相近的模式类合并为一类；相反，如果神经元节点数多于类别数，则有可能分的过细，或者是出现“死节点”，即在训练过程中，某个节点从未获胜过且远离其他获胜节点，因此它们的权值从未得到过更新。
不过一般来说，如果对类别数没有确定知识，宁可先设定较多的节点数，以便较好的映射样本的拓扑结构，如果分类过细再酌情减少输出节点。