一维不定常流-笔记

《高等流体力学》学习笔记王恒宇113121001183重点实验室一维非定常流动中的特征线方程和特征关系一、概念特征曲线：对于双曲型方程组，在x，t平面有一系列曲线，若在这些曲线上，任意给定物理参数的值作为Cauchy问题的初始值，这样Cauchy问题的解一般是不存在的。

这些曲线称为方程组的特征曲线。

特征关系：对在这些曲线上的物理参数或未知函数的值给定一定的关系式。

二、推导设x=x(t)为某一特征曲线，在这条曲线上给定u(t)，ρ(t)，S(t)的值。

研究下面方程组的Cauchy问题∂ρ∂t +u∂ρ∂x+ρ∂u∂x=0，ρ∂u ∂t +ρu∂u∂x+∂p∂x=0，（1）∂S∂t+u∂S∂x=0，p=f(ρ,S)。

求解这个问题即要在x=x(t)上求出∂u∂t ，∂u∂x，∂ρ∂t，∂p∂x，∂S∂t，∂S∂x的值。

六个一级微商满足以下六个方程∂ρ∂t +u∂ρ∂x+ρ∂u∂x=0，S∂u ∂t +pρ∂ρ∂x+ρu∂u∂x+p S∂S∂x=0，∂S ∂t +u∂S∂x=0，（2）dt ∂ρ∂t +dx ∂ρ∂x =dρ， dt ∂u ∂t +dx ∂u ∂x =du ， dt∂S ∂t+dx∂S ∂x=dS 。

由于x=x(t)是特征曲线，上方程组无解。

因此，x=x(t)应使该方程组系数行列式等于零，即||100u ρ00ρ0p ρρu p S 00100u dt 00dx 000dt 00dx 000dt 00dx ||=0 （3） 化简得，|udt −dx ρdt 0p ρdtρudt −ρdx p S dt 00udt −dx|=ρ(udt −dx )3−ρp ρ(udt −dx )dt 2=0由于p ρ=c 2，可解得：dx dt=u ，u +c ，u −c （4）即方程组（1）的三族不同的特征线。

通过特征线方程可求出相应于每条特征线的特征关系式，这些关系式应使方程组（2）有解。

这样用方程组（2）的自由项（0，0，0，d ρ，du ，dS ）来代替行列式（3）中的任意一行时，所得到的新的行列式应该等于零。

流体力学复习资料1.流体的定义；宏观：流体是容易变形的物体，没有固定的形状。

微观：在静力平衡时，不能承受拉力或者剪力的物体就是流体。

2. 流体的压缩性：温度一定时，流体的体积随压强的增加而缩小的特性。

流体的膨胀性：压强一定时，流体的体积随温度的升高而增大的特性。

3. 黏度变化规律：液体温度升高，黏性降低；气体温度升高，黏性增加。

原因：液体黏性是分子间作用力产生；气体黏性是分子间碰撞产生。

4.牛顿内摩擦定律：运动的额流体所产生的内摩擦力F的大小与垂直于流动方向的速度梯度du/dy成正比，与接触面的面积A成正比，并与流体的种类有关，与接触面上的压强无关。

数学表达式：F=μA du/dy流层间单位面积上的内摩擦力称为切向应力τ=F/A=μdu/dy5.静止流体上的作用力：质量力、表面力。

质量力：指与流体微团质量大小有关并且集中作用在微团质量中心上的力。

表面力：指大小与流体表面积有关并且分布作用在流体表面上的力。

6.重力作用下静力学基本方程：dp=-ρgdz 对于均质不可压缩流体：z+p/ρ=c物理意义：几何意义7. .绝对压强：以绝对真空为基准计算的压强。

P相对压强：以大气压强为基准计算的压强。

P e真空度：某点的压强小于大气压强时，该点压强小于大气压强的数值。

P vP=p a+ρgh p e=p-pa p v=p a-p8.压力提的概念：所研究的曲面（淹没在静止液体中的部分）到自由液面或自由液面的延长面间投影所包围的一块空间体积。

液体在曲面上方叫实压力体或正压力体；下方的叫虚压力体或负压力体。

9. 研究流体运动的两种方法：①拉格朗日法②欧拉法10.定常流动：流体质点的运动要素只是坐标的函数而与时间无关。

非定常流动：流体质点的运动要素既是坐标的函数又是时间的函数。

11. 迹线：指流体质点的运动轨迹，它表示了流体质点在一段时间内的运动情况。

流线：在流场中每一点上都与速度矢量相切的曲线称为流线。

流线是同一时刻不同流体质点所组成的曲线，它给出该时刻不同流体质点的速度方向。

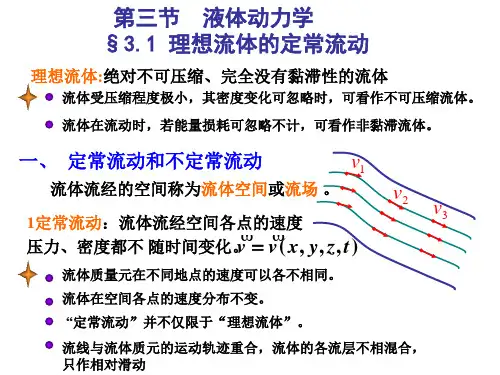
定常流动流体（气体、液体）流动时，若流体中任何‎一点的压力，速度和密度等‎物理量都不随‎时间变化，则这种流动就‎称为定常流动‎；反之，只要压力，速度和密度中‎任意一个物理‎量随时间而变‎化，液体就是作非‎定常流动或者‎说液体作时变‎流动。

所以，定常流动时，管中流体每单‎位时间流过的‎体积(体积流量)qV为常量，流体每单位体‎积的质量(密度)ρ也是常量。

非定常流动流体的流动状‎态随时间改变‎的流动。

若流动状态不‎随时间而变化‎，则为定常流动‎。

流体通常的流‎动几乎都是非‎定常的。

分类按流动随时间‎变化的速率，非定常流动可‎分为三类：①流场变化速率‎极慢的流动：流场中任意一‎点的平均速度‎随时间逐渐增‎加或减小，在这种情况下‎可以忽略加速‎度效应，这种流动又称‎为准定常流动‎。

水库的排灌过‎程就属于准定‎常流动。

可认为准定常‎流动在每一瞬‎间都服从定常‎流动的方程，时间效应只是‎以参量形式表‎现出来。

②流场变化速率‎很快的流动：在这种情况下‎须考虑加速度‎效应。

活塞式水泵或‎真空泵所造成‎的流动，飞行器和船舶‎操纵问题中所‎考虑的流动都‎属这一类。

这类流动和定‎常流动有本质‎上的差别。

例如，用伯努利方程‎（见伯努利定理‎）描述这类流动‎，就须增加一个‎与加速度有关‎的项，成为：,式中为理想流‎体沿流线的速‎度分布；A和B表示同‎一流线上的两‎个点;P 为压强;为密度；g为重力加速‎度；z为重力方向‎上的坐标；ds为流线上‎的长度元。

③流场变化速率‎极快的流动：在这种情况下‎流体的弹性力‎显得十分重要‎，例如瞬间关闭‎水管的阀门。

阀门突然关闭‎时，整个流场中流‎体不可能立即‎完全静止下来‎，速度和压强的‎变化以压力波‎（或激波）的形式从阀门‎向上游传播，产生很大的振‎动和声响，即所谓水击现‎象。

这种现象不仅‎发生在水流中‎，也发生在其他‎任何流体中。

在空气中的核‎爆炸也会发生‎类似现象。

除上述三类流‎动外，某些状态反复‎出现的流动也‎被认为是一种‎非定常流动。

1.渗流：流体在多孔介质中流动叫做渗流。

渗透率为压力梯度为1时，动力黏滞系数为l的液体在介质中的渗透速度。

是表征土或岩石本身传导液体能力的参数。

其大小与孔隙度、液体渗透方向上空隙的几何形状、颗粒大小以及排列方向等因素有关，而与在介质中运动的液体性质无关。

渗透率（k）用来表示渗透性的大小。

在一定压差下，岩石允许流体通过的性质称为渗透性；在一定压差下，岩石允许流体通过的能力叫渗透率。

2.开敞式油藏：如果油气藏外围与天然水源相连通，可向油气藏供液就是开敞式油气藏。

如果外围封闭且边缘高程与油水界面高程一致则称为封闭式油藏。

3.原始地层压力：油气藏开发以前，一般处于平衡状态，此时油层的流体所承受的压力叫原始地层压力。

4.供给压力：油气藏中存在液源供给区时，在供给边缘上的压力称为供给压力。

5.驱动方式可分为：水压驱动，弹性驱动，溶解气驱动和重力驱动。

6.在渗流过程中，如果运动的各主要元素只随位置变化而与时间没有关系，则称为稳定流。

反之，若各主要元素之一与时间有关，则称为非定常渗流或者不稳定渗流。

7.渗流的基本方式：平面一维渗流，平面径向渗流，和球面渗流。

8.绘制渗流图时规定这样的原则：任何相邻两条等压线之间的压差必须相等，同时，任何两条流线之间的流量必须相等。

9.井底结构和井底附近地区油层性质发生变化的井称为渗流不完善井。

不完善井可以分为打开程度不完善，打开性质不完善，双重不完善井。

10.试井：直接从实测的产量压力数据反求地层参数，然后用求得的地层参数来预测新的工作制度下的产量。

11.井间干扰：油水井工作制度的变化以及新井的投产会使原来的压力分布状态遭受到破坏引起整个渗流场发生变化，自然会影响到邻井的产量，这种井间相互影响的现象称为井间干扰。

12.压降叠加原理：多井同时工作时，地层中任一点外的压降等于各井以各自不变的产量单独工作时在该点处造成的压降代数和。

13.势的叠加原理：如果均质等厚不可压缩无限大底层上有许多点源，点汇同时工作，我们自然会想到地层上任一点的势应该等于每个点源点汇单独工作时在该点所引起的势的代数和，这就是势的叠加原理。

一维非定常连续流动一维非定常流动是指气流的速度和热力学参数仅与时间t和一个坐标变量x有关的流动，也就是说，在某一时刻，在任何一个垂直于x轴的平面上，气流的速度和热力学参数是不变的。

它包括连续流（等熵波）和间断流（激波、接触面）。

下面主要介绍连续流。

在进行讨论之前，首先假定气体为常比热完全气体（或称量热完全气体），忽略气流的粘性和热传导作用，流动过程是等熵的。

作为理解非定常连续流动的基础，首先介绍小扰动波的产生，传播及其简化分析。

一、小扰动波1.产生小扰动是指气流的速度和热力学参量的相对变化量都很小，例如声波就是一种小扰动波，它以声速传播，因此，通常人们把小扰动在介质中的传播速度称为声速。

对介质的扰动形式有很多，但总归起来不外乎速度不匹配和压力不平衡。

下面将要介绍的是由于活塞运动引起速度不匹配所产生的波。

在一个等截面无限长的圆管中，初始时刻，活塞及其两边的气体处于静止状态。

设活塞在很短的时间内，速度增加至du。

此后，它以匀速向右运动。

这时，活塞左右两边的气体同时受到一个微弱的扰动：右边的气体被压缩，左边的气体变得稀疏，其效果以小扰动波的形式向两边传播。

这种波通过以后，波后气体均以活塞的速度向右运动。

同时，右边气体压力增加一个微量dp，左边气体减小一个微量dp，这两种波分别称为小扰动压缩波和小扰动稀疏波。

上述两类小扰动波得传播过程在(x，t)图上的图示法如下压缩波通过以后，波后气流速度方向与波面传播方向一致，质点迹线靠近波面迹线；稀疏波通过以后，波后气流速度方向与波面传播方向相反，质点迹线偏离波面迹线。

对于运动的气体，压缩波后气体被加速，稀疏波后气体被减速。

2.传播定义向右为x轴的正方向，如果气体本身以u（代数值）的速度在运动，则波的传播速度为定义以速度(u+a)传播的波为“右行波”，以速度(u-a)传播“左行波”。

对于右行波而言，气体质点一定从右边（x轴正向）进入波阵面，对于左行波而言，气体质点一定从左边（x轴负向）进入2. 小扰动波的简化物理分析以一道右行小扰动波为例进行分析。

一维非定常连续流动集团档案编码：[YTTR-YTPT28-YTNTL98-UYTYNN08]一维非定常连续流动一维非定常流动是指气流的速度和热力学参数仅与时间t 和一个坐标变量x 有关的流动，也就是说，在某一时刻，在任何一个垂直于x 轴的平面上，气流的速度和热力学参数是不变的。

它包括连续流（等熵波）和间断流（激波、接触面）。

下面主要介绍连续流。

在进行讨论之前，首先假定气体为常比热完全气体（或称量热完全气体），忽略气流的粘性和热传导作用，流动过程是等熵的。

作为理解非定常连续流动的基础，首先介绍小扰动波的产生，传播及其简化分析。

一、 小扰动波1. 产生小扰动是指气流的速度和热力学参量的相对变化量都很小，例如声波就是一种小扰动波，它以声速传播，因此，通常人们把小扰动在介质中的传播速度称为声速。

对介质的扰动形式有很多，但总归起来不外乎速度不匹配和压力不平衡。

下面将要介绍的是由于活塞运动引起速度不匹配所产生的波。

在一个等截面无限长的圆管中，初始时刻，活塞及其两边的气体处于静止状态。

设活塞在很短的时间内，速度增加至du 。

此后，它以匀速向右运动。

这时，活塞左右两边的气体同时受到一个微弱的扰动：右边的气体被压缩，左边的气体变得稀疏，其效果以小扰动波的形式向两边传播。

这种波通过以后，波后气体均以活塞的速度向右运动。

同时，右边气体压力增加一个微量dp ，左边气体减小一个微量dp ，这两种波分别称为小扰动压缩波和小扰动稀疏波。

上述两类小扰动波得传播过程在(x ，t )图上的图示法如下压缩波通过以后，波后气流速度方向与波面传播方向一致，质点迹线靠近波面迹线；稀疏波通过以后，波后气流速度方向与波面传播方向相反，质点迹线偏离波面迹线。

对于运动的气体，压缩波后气体被加速，稀疏波后气体被减速。

2.传播定义向右为x 轴的正方向，如果气体本身以u （代数值）的速度在运动，则波的传播速度为dd dd=d ±d定义以速度(u+a )传播的波为“右行波”，以速度(u-a )行波”。

一维不定常流体运动【参考文献】L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Chapter 10.Ya. B. Zel ’dovich and Yu. P. Raizer, Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena, Chapter 1.我们简要学习理想流体的一维不定常流动，可以帮助我们理解ICF 中的流体力学过程。

对于理想流体，在不出现参数发生跃变的情况下，流体的熵是个常数，即 0.u s t x ∂∂⎡⎤+=⎢⎥∂∂⎣⎦如果初始时刻流体的参数不依赖于空间变量，那么流体的熵始终保持不变。

在这种情况下，流体的密度仅依赖于压强，().p ρρ=就只考虑流体的连续性方程和动量方程，()0,10.u t x u u p u t x x ρρρ∂∂+=∂∂∂∂∂++=∂∂∂ 利用绝热方程，连续性方程的形式可以改写为， 210s u u u u t x x p t x u u p c t x xρρρρρ⎛⎞∂∂∂∂∂∂∂⎡⎤⎡⎤++=++⎜⎟⎢⎥⎢⎥p x ∂∂∂∂∂∂⎣⎦⎣⎦⎝⎠∂∂∂⎡⎤=++⎢⎥∂∂∂⎣⎦=∂ 或10.p u p u c c t c x x ρ∂∂∂++=∂∂∂ 这个方程与动量方程结合，可以得到如下两个方程，1()()1()()u c u u c p t x c t x u c u u c p t x c t x ρρ∂∂∂∂⎡⎤⎡⎤+++++=⎢⎥⎢⎥∂∂∂∂⎣⎦⎣⎦∂∂∂∂⎡⎤⎡⎤+−−+−=⎢⎥⎢⎥∂∂∂∂⎣⎦⎣⎦0,0. 引入所谓的特征线，:,:,dx C u dt dx C u dt +−c c =+=− 那么沿着特征线C +，有如下方程， 10,du dp cρ+= 那么沿着特征线C −，有如下方程， 10,du dp cρ−= 引入所谓的Riemann 不变量，其定义为J ±dp d J u u c c ρρρ±=±=±∫∫，那么沿着特征线，是个常数。

1． 从力学角度看，流体区别于固体的特点是：易变形性，可压缩性,粘滞性和表面张力。

2． 牛顿流体: 在受力后极易变形,且切应力与变形速率成正比的流体。

即τ=μ＊du/dy 。

当n<1时，属假塑性体。

当n=1时，流动属于牛顿型。

当n>1时，属胀塑性体.3． 流场： 流体运动所占据的空间。

流动分类 时间变化特性： 稳态与非稳态空间变化特性： 一维，二维和三维流体内部流动结构： 层流和湍流流体的性质： 黏性流体流动和理想流体流动；可压缩和不可压缩流体运动特征： 有旋和无旋；引发流动的力学因素： 压差流动，重力流动,剪切流动4. 描述流动的两种方法：拉格朗日法和欧拉法拉格朗日法着眼追踪流体质点的流动，欧拉法着眼在确定的空间点上考察流体的流动5。

迹线：流体质点的运动轨迹曲线流线：任意时刻流场中存在的一条曲线，该曲线上各流体质点的速度方向与该曲线的速度方向一致性质 a 。

除速度为零或无穷大的点以外，经过空间一点只有一条流线 b.流场中每一点都有流线通过，所有流线形成流线谱c ．流线的形状和位置随时间而变化，稳态流动时不变迹线和流线的区别：流线是同一时刻不同质点构成的一条流体线；迹线是同一质点在不同时刻经过的空间点构成的轨迹线。

稳态流动下，流线与迹线是重合的。

6。

流管：流场中作一条不与流线重合的任意封闭曲线，通过此曲线的所有流线构成的管状曲面. 性质：①流管表面流体不能穿过.②流管形状和位置是否变化与流动状态有关。

7．涡量是一个描写旋涡运动常用的物理量.流体速度的旋度▽xV 为流场的涡量。

有旋流动：流体微团与固定于其上的坐标系有相对旋转运动。

无旋运动：流场中速度旋度或涡量处处为零.涡线是这样一条曲线,曲线上任意一点的切线方向与在该点的流体的涡量方向一致。

8. 静止流体：对选定的坐标系无相对运动的流体.不可压缩静止流体质量力满足 ▽x f =09。

匀速旋转容器中的压强分布p=ρ(gz -22r2ω）+c10. 系统:就是确定不变的物质集合。