5三角函数值在各象限的符号

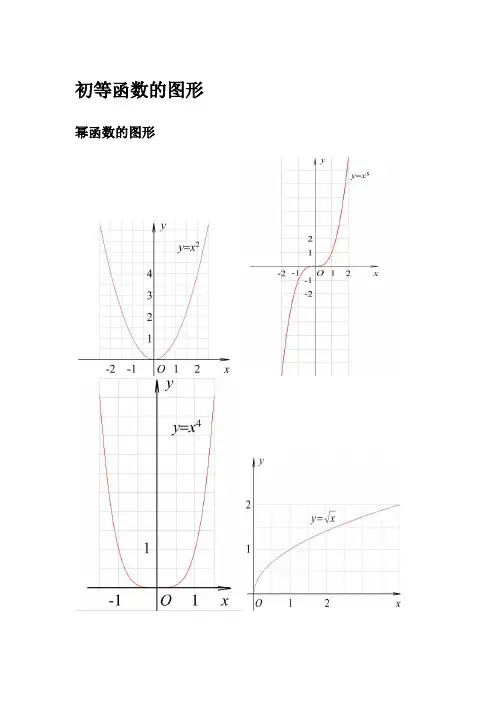
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscαcosα·secαtanα·cotα三角函数的性质函数y=sinx y=cosx y=tanx y=cotx定义域R R ｛x｜x∈R且x≠kπ+2π,k∈Z｝｛x｜x∈R且x≠kπ,k∈Z｝值域［-1，1］x=2kπ+2π时y max=1x=2kπ-2π时y min=-1［-1,1］x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在［2kπ-2π,2kπ+2π］上都是增函数；在［2kπ+2π,2kπ+32π］上都是减函数(k∈Z)在［2kπ-π，2kπ］上都是增函数；在［2kπ，2kπ+π］上都是减函数(k∈Z)在(kπ-2π，kπ+2π)内都是增函数(k∈Z)在(kπ，kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数，叫做反正弦函数，记作x=arsinyy=cosx(x∈〔0,π〕)的反函数，叫做反余弦函数，记作x=arccosyy=tanx(x∈(-2π,2π)的反函数，叫做反正切函数，记作x=arctanyy=cotx(x∈(0,π))的反函数，叫做反余切函数，记作x=arccoty理解arcsinx表示属于［-2π,2π］且正弦值等于x的角arccosx表示属于［0，π］，且余弦值等于x的角arctanx表示属于(-2π,2π)，且正切值等于x的角arccotx表示属于(0，π)且余切值等于x的角性质定义域［-1，1］［-1，1］(-∞，+∞)(-∞，+∞)值域［-2π，2π］［0，π］(-2π，2π)(0，π)单调性在〔-1，1〕上是增函数在［-1，1］上是减函数在(-∞，+∞)上是增数在(-∞，+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈［-1，1］)arcsin(sinx)=x(x∈［-2π,2π］)cos(arccosx)=x(x∈［-1,1］)arccos(cosx)=x(x∈［0,π］)tan(arctanx)=x(x∈R)arctan(tanx)=x（x∈(-2π,2π)）cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=2π(x∈［-1,1］)arctanx+arccotx=2π(X∈R)三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-cosAsinB cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=tanAtanB -1tanBtanA +tan(A-B)=tanAtanB 1tanBtanA +-cot(A+B)=cotA cotB 1-cotAcotB +cot(A-B)=cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA 2-Sin2A=2SinA•CosACos2A =Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A =3sinA-4(sinA)3cos3A =4(cosA)3-3cosA tan3a =tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=AA cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba -sina-sinb=2cos 2b a +sin2ba -cosa+cosb =2cos 2b a +cos2ba -cosa-cosb =-2sin 2b a +sin2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb =-21[cos(a+b)-cos(a-b)]cosacosb =21[cos(a+b)+cos(a-b)]sinacosb =21[sin(a+b)+sin(a-b)]cosasinb =21[sin(a+b)-sin(a-b)]sin(-a)=-sina cos(-a)=cosa sin(2π-a)=cosa cos(2π-a)=sina sin(2π+a)=cosa cos(2π+a)=-sinasin(π-a)=sina cos(π-a)=-cosa sin(π+a)=-sina cos(π+a)=-cosatgA=tanA =aacos sin 万能公式sina=2)2(tan 12tan2aa +cosa=22)2(tan 1)2(tan 1aa+-tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c)[其中tanc=a b ]a•sin(a)-b•cos(a)=)b (a 22+×cos(a-c)[其中tan(c)=b a ]1+sin(a)=(sin 2a +cos 2a )21-sin(a)=(sin 2a -cos 2a )2其他非重点三角函数csc(a)=asin 1sec(a)=a cos 1双曲函数sinh(a)=2e -e -aa cosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a 公式一设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）=sinαcos （2kπ＋α）=cosαtan （2kπ＋α）=tanαcot （2kπ＋α）=cotα设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）=-sinαcos（π＋α）=-cosαtan（π＋α）=tanαcot（π＋α）=cotα公式三任意角α与-α的三角函数值之间的关系：sin（-α）=-sinαcos（-α）=cosαtan（-α）=-tanαcot（-α）=-cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）=sinαcos（π-α）=-cosαtan（π-α）=-tanαcot（π-α）=-cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）=-sinαcos（2π-α）=cosαtan（2π-α）=-tanαcot（2π-α）=-cotα2π±α及23π±α与α的三角函数值之间的关系：sin （2π+α）=cosαcos （2π+α）=-sinαtan （2π+α）=-cotαcot （2π+α）=-tanαsin （2π-α）=cosαcos （2π-α）=sinαtan （2π-α）=cotαcot （2π-α）=tanαsin （23π+α）=-cosαcos （23π+α）=sinαtan （23π+α）=-cotαcot （23π+α）=-tanαsin （23π-α）=-cosαcos （23π-α）=-sinαtan （23π-α）=cotαcot （23π-α）=tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+B•sin(ωt+φ)=)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明（全部）公式表达式乘法与因式分解a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注：韦达定理判别式b2-4a=0注：方程有相等的两实根b2-4ac>0注：方程有一个实根b2-4ac<0注：方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A)ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB-ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注：角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r>0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦：cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减，可以得到2组积化和差:相加：cosAcosB=[cos(A+B)+cos(A-B)]/2相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减，可以得到2组积化和差:相加：sinAcosB=[sin(A+B)+sin(A-B)]/2相减：sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β),|m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。

【课题】
5．3 . 2各象限角的三角函数值的正负号
【教学目标】
知识目标：
理解三角函数在各象限的正负号；
能力目标：
会判断任意角三角函数的正负号；
情感目标：
由三角函数的概念推导出任意角的三角函数值、三角函数的正负号以及界限角的三角函数值使学生体会到数学知识的内在统一性.
【教学重点】
三角函数在各象限的符号；
【教学难点】
任意角的三角函数值符号的确定．
【教学设计】
（1）在知识回顾中推广得到新知识；
（2）利用定义认识各象限角三角函数的正负号；
（3）问题引领，师生互动．在问题的思考和交流中，提升能力.
【教学备品】【教师】
教学课件，投影仪，黑板．梁金明
【课时安排】【教学对象】
第五周星期二第3节1课时 15会计1
【教学过程】
sin
y
r
α=；cos
x
r
α=；tan
y
x
α=．
*揭示课题 5.3各象限角的三角函数值的正负号
*动脑思考探索新知
由于0
r>，所以任意角三角函数的正负号由终边上点坐标来确定限．
0，cos4320
>，tan432
8π2π8π。

4.3.2三角函数在个象限的符号我们学习了任意角的三角函数，知道了对于任意角的三角函数我们是在坐标系里定义的，究竟是怎么定义的呢，咱们就来回顾回顾。

假设α是任意角，假设这条射线就是它的终边，然后我们在终边上任取一点P，坐标设为（x,y)，然后P到原点的距离我们记为r,接着就是6个三角函数的定义。

首先正弦等于谁比上谁，余弦呢？。

接下来就是见证奇迹的时刻了，大家看正弦和余割他们两个什么关系？余弦和正割呢？互为倒数，然后正切和余切也互为倒数，这是很久很久以前的事情了，咱就不提啦。

现在上面三个函数和下面三个函数分别互为倒数，如果上面的为正，那下面的呢？也为正，如果上面的为负呢？下面的也为负，也就是说它们的符号一致，因此如果要我们判断他们六个的正负的话，只需判断上面三个就OK了。

接下来我们这节课的工作重心就是判断这三个函数在各个象限的正负情况。

首先看正弦，sinα=，r因为表示的P到原点的距离，始终为正，因此我们只需判断y的正负。

在第一象限y是正还是负？正，因此正弦在第一象限为正，第二象限呢？正，第三象限呢？负，第四象限呢？负。

好，总结一下也就是说正弦在一二象限为证。

接下来我们看一下余弦，cosα=，同样因为r始终为正，我们只需判断x.在第一象限，横坐标大于0还是小于0？大于0因此余弦为正，在第二象限横坐标为正还是为负？因此余弦小于0，。

，。

，总结一下，余弦在哪几个象限为正？一四。

最后看一下正切，tanα=，等于纵坐标比上横坐标，大家想一下正切什么时候大于0呢？当x和y同号的时候，那x和y在哪几个象限同号呢？一三象限，因此正切就在一三象限为正，剩下的两个象限自然就为负了。

余切呢因为和正切互为倒数，正负相同，因此余切也在一三为正、二四为负，因此这个图还可以用来表示余切的正负。

对于正割和余割，我们在高中不作深入研究，因此我们这里就不讨论了，大家只要掌握它们俩是怎么定义的就OK了。

刚才呢咱们是从函数的角度来研究的，接下来我们从象限的角度来探讨探讨。

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscαcosα·secαtanα·cotα反三角函数的图形设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα公式三任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα三角函数公式证明（全部）公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注：韦达定理判别式b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注：角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。

三角函数公式、图像大全幂函数的图形指数函数的图形对数函数的图形三角函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα 三角函数的性质函数 y=sinx y=cosx y=tanxy=cotx 定义域 R R ｛x｜x∈R且x≠kπ+,k∈Z｝｛x｜x∈R且x≠kπ,k∈Z｝值域［-1，1］x=2kπ+ 时ymax=1 x=2kπ- 时ymin=-1 ［-1,1］x=2kπ时ymax=1 x=2kπ+π时ymin=-1 R 无最大值无最小值 R 无最大值无最小值周期性周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数单调性在［2kπ-,2kπ+ ］上都是增函数；在［2kπ+ ,2kπ+π］上都是减函数(k∈Z)在［2kπ-π，2kπ］上都是增函数；在［2kπ，2kπ+π］上都是减函数(k∈Z)在(kπ-，kπ+)内都是增函数(k∈Z)在(kπ，kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-, 〕的反函数，叫做反正弦函数，记作x=arsiny y=cosx(x∈〔0,π〕)的反函数，叫做反余弦函数，记作x=arccosy y=tanx(x∈(- , )的反函数，叫做反正切函数，记作x=arctany y=cotx(x∈(0,π))的反函数，叫做反余切函数，记作x=arccoty 理解 arcsinx表示属于［-,］且正弦值等于x的角 arccosx表示属于［0，π］，且余弦值等于x的角 arctanx表示属于(-,)，且正切值等于x的角arccotx表示属于(0，π)且余切值等于x的角性质定义域［-1，1］［-1，1］ (-∞，+∞)(-∞，+∞)值域［-，］［0，π］ (-，)(0，π)单调性在〔-1，1〕上是增函数在［-1，1］上是减函数在(-∞，+∞)上是增数在(-∞，+∞)上是减函数奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanx arccot(-x)=π-arccotx 周期性都不是同期函数恒等式sin(arcsinx)=x(x∈［-1，1］)arcsin(sinx)=x(x∈［-,］) cos(arccosx)=x(x∈［-1,1］)arccos(cosx)=x(x∈［0,π］)tan(arctanx)=x(x∈R)arctan(tanx)=x（x∈(-,)）cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=(x∈［-1,1］)arctanx+arccotx=(X∈R)三角函数公式两角和公式 sin(A+B)= sinAcosB+cosAsinB sin(A-B)= sinAcosB-cosAsinB cos(A+B)= cosAcosB-sinAsinB cos(A-B)= cosAcosB+sinAsinB tan(A+B)= tan(A-B)= cot(A+B)= cot(A-B)= 倍角公式tan2A = Sin2A=2SinA•CosA Cos2A = Cos2A-Sin2A=2Cos2A-1=1-2sin2A 三倍角公式 sin3A =3sinA-4(sinA)3 cos3A =4(cosA)3-3cosA tan3a = tana·tan(+a)·tan(-a) 半角公式 sin()= cos()= tan()= cot()= tan()== 和差化积sina+sinb=2sincos sina-sinb=2cossin cosa+cosb =2coscos cosa-cosb =[cos(a+b)-cos(a-b)] cosacosb =[cos(a+b)+cos(a-b)] sinacosb = [sin(a+b)+sin(a-b)] cosasinb = [sin(a+b)-sin(a-b)] 诱导公式 sin(-a) =a)= cosa sin(-a)= cosa cos(-a)= sina sin(+a)= cosa cos(+a)=a)= sina cos(π-a)=sina cos(π+a)=b•cos(a)= ×cos(a-c)[其中tan(c)=]1+sin(a)=(sin+cos)21-sin(a)= (sin-cos)2 其他非重点三角函数 csc(a)= sec(a)= 双曲函数 sinh(a)= cosh(a)= tg h(a)= 公式一设α为任意角，终边相同的角的同一三角函数的值相等： sin（2kπ＋α）= sinα cos（2kπ＋α）= cosα tan（2kπ＋α）= tanα cot（2kπ＋α）= cotα 公式二设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin（π＋α）=cosα tan（π＋α）= tanα cot（π＋α）= cotα 公式三任意角α与α）=α）= cosα tan（-α）=α）=α与α的三角函数值之间的关系： sin（π-α）= sinα cos（π-α）=α）=α）=和公式三可以得到2π-α与α的三角函数值之间的关系： sin（2π-α）=α）= cosα tan（2π-α）=α）=sinα tan（+α）=tanα sin（-α）= cosα cos（-α）= sinα tan （-α）= cotα cot（-α）= tanα sin（+α）=cotα cot（+α）=α）=α）=α）= cotα cot（-α）= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ)=×sin 三角函数公式证明（全部）公式表达式乘法与因式分解 a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b-b≤a≤b |a-b|≥|a|-|b|b+√(b2-4ac)/2ab+√(b2-4ac)/2a 根与系数的关系 X1+X2=-b/a X1*X2=c/a 注：韦达定理判别式 b2-4a=0 注：方程有相等的两实根 b2-4ac>0 注：方程有一个实根b2-4ac0 抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py 直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c *h 正棱锥侧面积 S=1/2c*h 正棱台侧面积 S=1/2(c+c )h 圆台侧面积S=1/2(c+c )l=pi(R+r)l 球的表面积 S=4pi*r2 圆柱侧面积S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l 弧长公式 l=a*r a 是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h 斜棱柱体积 V=S L 注：其中,S 是直截面面积， L是侧棱长柱体体积公式 V=s*h 圆柱体 V=pi*r2h------------------------------------------------------------------------------------------ 三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦： cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB 这两式相加或相减，可以得到2组积化和差: 相加：cosAcosB=[cos(A+B)+cos(A-B)]/2 相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2 sin(A+B)=sinAcosB+sinBcosA sin(A-B)=sinAcosB-sinBcosA 这两式相加或相减，可以得到2组积化和差: 相加：sinAcosB=[sin(A+B)+sin(A-B)]/2 相减：sinBcosA=[sin(A+B)-sin(A-B)]/2 这样一共4组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负 .3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC（2）sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 . 已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。

幂函数的图形指数函数的图形对数函数的图形数的图形三角函各三角函数值在各象限的符号cosα·secαtanα·cotαsinα·cscα三角函数的性质函数y=cosxy=sinx y=tanx y=cotx且R｛x｜x∈｜xx∈R 且｛定义域RR Z｝x≠kπ,k∈Z,k∈｝x≠kπ+ 2［-1,1］Rπ+x=2k 时［-1，1］R时=1y x=2kπ2max无最大值无最大值值域y x=2k π+π时=-1y=1minmax无最小值无最小值时y=-1x=2kπ-min2周期性周期为2π周期为ππ周期为周期为2π奇函数奇函数奇偶性偶函数奇函数．在［2kπ-π，2kπ］上都是在(kπ，kπ+π)内都］,2kπ+在(kπ-，kπ+)内都2kπ-在［增函数；在是减函数(k∈Z)2222［2kπ，2kπ+π］上都是上都是增函数；在是增函数(k∈Z)单调性减函数(k∈Z)2］上,2k π+π［2kπ+32(k∈Z)都是减函数反三角函数的图形反三角函数的性质反余切函反正弦函反余弦函反正切函名称y=cotx((0,π)y=cosx(∈0),-y=tanx(x∈(-y=sinx(x∈〔,反函数，叫做反余的反函数，叫做反2222 切函数，记作余弦函数，记作〕的反函数，叫做反的反函数，叫做反正切定义正弦函数，记作x=arccotyx=arccosyx=arctany函数，记作x=arsiny表示属于arccotx arccosx 表示属于表示属于［-arcsinx , 表示属于(-arctanx(0，π)且余切值等于2π］，且余弦，［0］,的角x 的角x 值等于22 理解x)，且正切值等于的角且正弦值等于x2的角定义域+∞)，［-1，1］(-∞，1］∞(-，+∞)［-1值域π)(0］，［0，π)(-，［-，］ 2 22 2性上是增数，+∞)在(-∞1〕上是增函+∞)上是减1］上是减，在［-1，在〔-1，(-在∞单调性质函数函数数arctan(-x)=-arctanxarccot(-x)=πarcsin(-x)=-arcsinxπarccos(-x)=-arccotx-奇偶性arccosx都不是同期函数周期性．cos(arccosx)R∈tan(arctanx)=x(x∈［∈-R)arcsin(arcsinx)=x(xcot(arccotx)=x(x) ∈［)-1,1］=x(x ］11，)arcsin(sinx) 2arccos(cosx) (0∈arccot(cotx)=x(x恒等式)∈［］-=x(x,,(- tan(tanx)=x（x∈,π))2 2)=x(x∈［0,π］）)2互余恒等式R)arcsinx+arccosx=(x∈［-1,1］)arctanx+arccotx=(X∈22公式三角函数A1 cos A)=tan(A cos12式和公两角sinAcosB+cosAsinB sin(A+B) =A cos 1A sinAcosB-cosAsinB =sin(A-B))=cot(A1 cos2cosAcosB-sinAsinB=cos(A+B) A sin A 1cos A cosAcosB+sinAsinB= cos(A-B) =)= tan( tanBtanA tan(A+B) =A A 1 cos2 sin tanAtanB 1- 和差化积tanB tanA= tan(A-B)b aa b tanAtanB 1cossina+sinb=2sin1-cotAcotB 2 2 cot(A+B) =b b a a cotAcotB sin sina-sinb=2cos1 cotAcotB2 2 a= cot(A-B)ba b cotA cotB cos2cos cosa+cosb = 2 2b a 公倍角式ab sincosa-cosb = -2sin 2tanA22 = tan2A2)b sin( a A 1tan tana+tanb=Sin2A=2SinA?CosA b coscos a22 2 2 A-1=1-2sin A Cos Cos2A= A-Sin A=2Cos积化和差式公角三倍1[cos(a+b)-cos(a-b)]sinasinb = - 32 3sinA-4(sinA)sin3A = 31 -3cosA 4(cosA)cos3A =[cos(a+b)+cos(a-b)]= cosacosb 2-a)tan(tan( ··+a)tana= tan3a133[sin(a+b)+sin(a-b)] sinacosb =21公半角式[sin(a+b)-sin(a-b)]cosasinb =2A1cos A)=sin( 12式公诱导A1cos A)=cos( -sina sin(-a) =12cosa=cos(-a)a a2-cos )1-sin(a) = (sin cosa -a) sin( =22 2 sina-a) cos( = 2其他非重点三角函数1= csc(a)cosa sin( =+a)sin a21= sec(a)= -sina+a) cos( cos a2sina πsin(-a) =。