初一数学拔高题复习

一、选择题（每题5分，共50分）1. 下列各数中，不是有理数的是（）A. 3.14B. -5C. $\sqrt{2}$D. $\frac{1}{3}$2. 如果$a > b$，那么下列不等式中正确的是（）A. $a + 2 > b + 2$B. $a - 2 < b - 2$C. $2a > 2b$D. $2a < 2b$3. 下列函数中，是反比例函数的是（）A. $y = x^2$B. $y = 2x - 3$C. $y = \frac{1}{x}$D. $y = \sqrt{x}$4. 在直角坐标系中，点A（2，3）关于x轴的对称点坐标是（）A.（2，-3）B.（-2，3）C.（-2，-3）D.（2，-3）5. 如果一个正方形的对角线长为10cm，那么这个正方形的面积是（）A. 25cm²B. 50cm²C. 100cm²D. 200cm²6. 下列各式中，完全平方公式正确的是（）A. $(a + b)^2 = a^2 + 2ab + b^2$B. $(a - b)^2 = a^2 - 2ab + b^2$C. $(a + b)^2 = a^2 - 2ab + b^2$D. $(a - b)^2 = a^2 + 2ab - b^2$7. 下列各式中，不是一元一次方程的是（）A. $2x + 3 = 7$B. $3(x - 2) = 9$C. $x^2 - 4 = 0$D. $4 - 2x = 5$8. 如果等腰三角形的底边长为6cm，腰长为8cm，那么这个三角形的面积是（）A. 24cm²B. 28cm²C. 32cm²D. 36cm²9. 下列各式中，不是勾股数的是（）A. $3, 4, 5$B. $5, 12, 13$C. $6, 8, 10$D. $7, 24, 25$10. 如果一个长方形的长是8cm，宽是6cm，那么这个长方形的对角线长是（）A. 10cmB. 12cmC. 14cmD. 16cm二、填空题（每题5分，共50分）1. 若$2x - 3 = 7$，则$x = $_________。

一、选择题（每题4分，共20分）1. 已知a、b是方程x^2-4x+3=0的两个实数根，则a+b的值是：A. 2B. 3C. 4D. 52. 下列各数中，有理数是：A. √2B. πC. 3.14D. -√23. 在下列各数中，绝对值最小的是：A. 2B. -3C. 0.5D. -2.54. 已知x=2，则代数式x^2-5x+6的值为：A. 1B. 3C. 5D. 75. 若a、b是方程x^2-3x+2=0的两个实数根，则a^2+b^2的值是：A. 4B. 5C. 6D. 7二、填空题（每题4分，共16分）6. 已知方程x^2-2x-3=0的解是x1、x2，则x1+x2=________，x1x2=________。

7. 若a、b是方程x^2-5x+6=0的两个实数根，则a^2+b^2=________。

8. 已知a、b是方程x^2-2x+1=0的两个实数根，则a^2+2ab+b^2=________。

9. 若x^2+3x-4=0的两个实数根分别为x1、x2，则x1+x2=________，x1x2=________。

10. 若x^2-3x+2=0的两个实数根分别为x1、x2，则x1^2+x2^2=________。

三、解答题（每题10分，共30分）11. （10分）已知方程x^2-4x+3=0的解是x1、x2，求（x1+x2）^2+2x1x2的值。

12. （10分）已知方程x^2-5x+6=0的解是x1、x2，求x1^2+x2^2+2x1x2的值。

13. （10分）已知方程x^2-2x+1=0的解是x1、x2，求x1^2+x2^2-x1x2的值。

答案：一、选择题1. C2. C3. C4. B5. A二、填空题6. 4，-37. 118. 19. -3，-410. 5三、解答题11. 1912. 3713. 2。

一、选择题（每题5分，共50分）1. 已知二次函数y=ax^2+bx+c（a≠0）的图象与x轴有两个交点A、B，且A（1，0），B（-3，0），则下列说法正确的是（）A. a>0，函数图象开口向上B. a<0，函数图象开口向上C. a>0，函数图象开口向下D. a<0，函数图象开口向下2. 已知函数y=2x-3，下列说法正确的是（）A. 函数图象是一条斜率为2的直线B. 函数图象是一条斜率为-3的直线C. 函数图象是一条斜率为2，y截距为-3的直线D. 函数图象是一条斜率为-3，y截距为2的直线3. 已知a，b是实数，且a+b=2，则下列说法正确的是（）A. a^2+b^2=5B. a^2+b^2=4C. a^2+b^2=6D. a^2+b^2=34. 已知正方形的对角线长度为10，则该正方形的面积是（）A. 25B. 50C. 100D. 2005. 已知一个等腰三角形的底边长为6，腰长为8，则该三角形的面积是（）A. 24B. 30C. 36D. 406. 已知一次函数y=kx+b（k≠0）的图象经过点A（1，2）和点B（3，-4），则下列说法正确的是（）A. k>0，b>0B. k>0，b<0C. k<0，b>0D. k<0，b<07. 已知一个等边三角形的边长为a，则该三角形的面积是（）A. a^2√3/4B. a^2√3/3C. a^2√3/2D. a^2√38. 已知一元二次方程x^2-4x+3=0的两个根分别为m和n，则下列说法正确的是（）A. m+n=4，mn=3B. m+n=3，mn=4C. m+n=4，mn=1D. m+n=3，mn=19. 已知函数y=|x-1|，则下列说法正确的是（）A. 函数图象是一条斜率为1的直线B. 函数图象是一条斜率为-1的直线C. 函数图象是一条斜率为1，y截距为1的直线D. 函数图象是一条斜率为-1，y截距为1的直线10. 已知一个长方形的面积是12，长是3，则该长方形的宽是（）A. 4B. 2C. 6D. 3二、填空题（每题5分，共50分）11. 已知二次函数y=ax^2+bx+c（a≠0）的图象与x轴有两个交点A、B，且A（2，0），B（-1，0），则该二次函数的解析式为______。

一、选择题（每题4分，共20分）1. 若方程 2x - 3 = 5 的解为 x = 3，则方程 4x + 6 = 2x - 12 的解为（）。

A. x = -9B. x = -6C. x = 6D. x = 92. 下列各组数中，成等差数列的是（）。

A. 2, 5, 8, 11B. 1, 3, 6, 10C. 4, 9, 16, 25D. 1, 2, 4, 83. 在平面直角坐标系中，点A（2，3）关于原点对称的点的坐标是（）。

A. （-2，-3）B. （2，-3）C. （-2，3）D. （3，-2）4. 若a，b，c是等比数列的前三项，且a + b + c = 12，abc = 27，则a的值为（）。

A. 1B. 3C. 9D. 275. 已知函数f(x) = x^2 - 4x + 4，那么f(x)的最小值为（）。

A. 0B. 1C. 2D. 4二、填空题（每题5分，共25分）6. 若等差数列{an}中，a1 = 3，公差d = 2，则第10项an = ________。

7. 在△ABC中，角A、B、C的对边分别为a、b、c，且a = 5，b = 7，c = 8，则角A的余弦值为 ________。

8. 已知等比数列{an}中，a1 = 2，公比q = 3，则第5项an = ________。

9. 在平面直角坐标系中，点P（-3，2）到直线y = 2x + 1的距离为 ________。

10. 若函数f(x) = ax^2 + bx + c的图像开口向上，且顶点坐标为（-1，2），则a = ________，b = ________。

三、解答题（每题10分，共30分）11. （10分）已知数列{an}的前n项和为Sn，且a1 = 1，an = an-1 + 2n - 1，求Sn的表达式。

12. （10分）在△ABC中，角A、B、C的对边分别为a、b、c，且a = 3，b = 4，c = 5，求sinB的值。

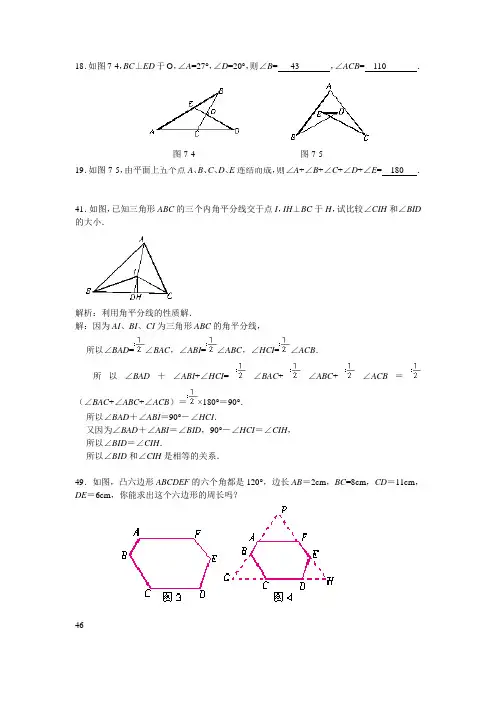
18．如图7-4，BC ⊥ED 于O ，∠A =27°，∠D =20°，则∠B = 43 ，∠ACB = 110 ．19．如图7-5，由平面上五个点A 、B 、C 、D 、E 连结而成，则∠A +∠B +∠C +∠D +∠E = 180 ．41．如图，已知三角形ABC 的三个内角平分线交于点I ，IH ⊥BC 于H ，试比较∠CIH 和∠BID 的大小．解析：利用角平分线的性质解．解：因为AI 、BI 、CI 为三角形ABC 的角平分线， 所以∠BAD =∠BAC ，∠ABI =∠ABC ，∠HCI =∠ACB ．所以∠BAD ＋∠ABI +∠HCI =∠BAC +∠ABC +∠ACB ＝（∠BAC +∠ABC +∠ACB ）＝×180°＝90°．所以∠BAD ＋∠ABI ＝90°－∠HCI ．又因为∠BAD ＋∠ABI ＝∠BID ，90°－∠HCI ＝∠CIH ， 所以∠BID ＝∠CIH ．所以∠BID 和∠CIH 是相等的关系．49．如图，凸六边形ABCDEF 的六个角都是120°，边长AB ＝2cm ，BC =8cm ，CD ＝11cm ，DE ＝6cm ，你能求出这个六边形的周长吗？46图7-4 图7-5AB1EF2CP Dxzy A BCFDE11． 如图所示,已知AB ∥CD,分别探索下列四个图形中∠P 与∠A,∠C 的关系,•请你从所得的四个关系中任选一个加以说明.PD CBA PDC BAP DCB APDCB A(1) (2) (3) (4)（1）分析：过点P 作PE//AB ∠APE+∠A+∠C=360° （2）∠P=∠A+∠C （3）∠P=∠C-∠A, （4）∠P=∠A-∠C12．如图，若AB//EF ，∠C= 90°，求x+y-z 度数。

分析：如图，添加辅助线证出：x+y-z=90°13．已知：如图，∠+∠=∠=∠BAP APD 18012，求证：∠=∠E F 分析：法一法二：由AB//CD 证明∠PAB=∠APC ， 所以∠EAP=∠APF 所以AE//FP21ABCD所以∠=∠E F7．⊿ABC 中，∠ABC 、∠ACB 的平分线相交于点O 。

初一数学《有理数》拓展提高试题 一选择题（每小题3分，共30分）1.某粮店出售三种品牌的面粉,袋上分别标有质量为(25±0.1)kg 、（25±0.2）kg 、 (25 ± 03)kg 的字样，从中任意拿出两袋 ，它们的质量最多相差( )A. 0.8kgB. 0.6kgC. 0.5kg D . 0.4kg2、有理数a 等于它的倒数，则a 2004是----------------------------------------------------（ ）Ａ.最大的负数 Ｂ.最小的非负数 Ｃ.绝对值最小的整数 Ｄ.最小的正整数 3、若0ab ≠，则a bab+的取值不可能是-----------------------------------------------（ ） A ．0 B.1 C.2 D.－2 4、=<3-x 3-x ,3则若x A 、1 B 、-1 C 、0 D 、25、如果有2005名学生排成一列，按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律报数，那么第2005名学生所报的数是……………………… （ ）A 、1B 、2C 、3D 、46、若|a|=4，|b|=2，且|a+b|=a+b, 那么a-b 的值只能是( ).A.2B. -2C. 6D.2或6 7、 x 是任意有理数，则2|x |+x 的值( ).A.大于零B. 不大于零C. 小于零D.不小于零 8、观察这一列数：34-，57, 910-, 1713,3316-，依此规律下一个数是（ ） A.4521 B.4519 C.6521 D.65199、下列各式中正确是（ ）（A ）22()a a =- （B ）33()a a =-（C ）33()aa =- （D ）33a a=10、的值为则满足有理数ab b b a a b a ,,,>-=A 正数B 负数C 负数或零D 非负数 二、填空题（每小题4分，共32分）11.请将3，4，－6，10这四个数用加减乘除四则运算以及括号组成结果为24的算式（每个数有且只能用一次）_______________ ______ ； 12.=--<)(0m m m ，则若 (－3)2013×( －31)2014= ； 13.20162015201620152015)()1(9)51,n m xyb a n m y x b a --+⨯-+（是它本身，求的相反数本身，的绝对值与倒数均是它互为倒数，互为相反数，与若.14绝对值大于-2.1而小于4.3的整数有 ，其和为 ．. 15.设c b a ,,为有理数，则由ccb b a a ++ 构成的各种数值是 16.设有理数a ，b ，c 在数轴上的对应点如图所示，则 │b-a │+│a+c │+│c-b•│=____ _ ___；17.2(1)20a b -++=，那么a b += 18、 读一读：式子“1+2+3+4+5+…+100”表示从1开始的100个连续自然数的和，由于上述式子比较长，书写也不方便，为了简便起见，我们可将“1+2+3+4+5+…+100”表示为1001n n =∑，这里“∑”是求和符号，例如“1+3+5+7+9+…+99”（即从1开始的100以内的连续奇数的和）可表示为501(21);n n =-∑又如“333333333312345678910+++++++++”可表示为1031n n=∑，同学们，通过以上材料的阅读，请解答下列问题：（1）2+4+6+8+10+…+100（即从2开始的100以内的连续偶数的和）用求和符号可表示为 ； （2）计算：521(1)n n=-∑= （填写最后的计算结果）。