圆的基本概念,作业

六年级上册数学教案《圆的认识》人教版一. 教材分析《圆的认识》是人教版六年级上册数学教材的一部分，主要让学生了解和掌握圆的基本概念、性质和简单的应用。

本节课的内容包括圆的定义、圆心、半径、直径、弧等基本概念，以及圆的周长和面积的计算方法。

通过本节课的学习，学生能够更好地理解圆的特征，提高解决实际问题的能力。

二. 学情分析六年级的学生已经具备了一定的空间想象能力和逻辑思维能力，他们对平面几何图形有了一定的了解。

但是，对于圆的一些基本概念和性质，学生可能还比较陌生。

因此，在教学过程中，教师需要注重引导学生掌握圆的基本概念，并通过大量的实践活动让学生加深对圆的认识。

三. 教学目标1.知识与技能：学生能够准确地描述圆的基本概念，掌握圆的周长和面积的计算方法。

2.过程与方法：学生通过观察、操作、思考、交流等过程，提高解决实际问题的能力。

3.情感态度与价值观：学生对数学产生浓厚的兴趣，培养合作意识和创新精神。

四. 教学重难点1.重点：圆的基本概念、性质和周长、面积的计算方法。

2.难点：圆的周长和面积的计算方法，以及如何在实际问题中灵活运用。

五. 教学方法1.情境教学法：通过生活情境导入，激发学生的学习兴趣。

2.动手操作法：让学生通过实际操作，加深对圆的认识。

3.合作交流法：引导学生分组讨论，培养合作意识和沟通能力。

4.归纳总结法：引导学生自主总结圆的性质和计算方法。

六. 教学准备1.准备一些圆形物品，如圆桌、圆形的玩具等，方便学生观察和操作。

2.准备圆的周长和面积的计算练习题，以及相关的实际问题。

七. 教学过程1.导入（5分钟）教师展示一些圆形物品，如圆桌、圆形的玩具等，引导学生观察并思考：这些物品有什么共同的特点？学生通过观察，发现它们都是圆形的。

教师趁机引入本节课的主题——圆的认识。

2.呈现（10分钟）教师通过多媒体课件或者黑板，呈现圆的基本概念、性质和周长、面积的计算方法。

在呈现过程中，教师引导学生积极参与，提问和解答问题。

圆的认识作业设计一、教学目标：1.知道圆的基本定义。

2.能够正确地使用圆的专有名词，如：半径、直径等。

3.理解圆的性质，如：圆的直径是半径的两倍、相交的两条弦相交于圆心等。

4.能够在实际问题中应用圆的知识，解决相关问题。

二、教学重难点：1.圆的性质和相关定理的掌握。

2.如何应用圆的知识解决实际问题。

三、教学准备：1.教学PPT。

2.课堂展示板。

3.直尺、圆规等绘图工具。

四、教学过程：Step 1：导入新课（5分钟）老师通过展示一些日常生活中的圆形物体的图片，让学生观察并讨论，引导学生认识到圆形在我们生活中的广泛存在，并提出与圆相关的问题。

Step 2：引入圆的定义（10分钟）老师通过使用PPT展示圆的定义，引导学生理解圆是由一条曲线上所有到定点的距离相等的点组成的。

并通过实际案例和图示帮助学生理解。

Step 3：介绍圆的专有名词（15分钟）老师通过使用课件，介绍圆的专有名词，如：半径、直径、弦、弧、切线等。

并让学生根据图像找出并标出这些名词，加深对这些术语的理解。

Step 4：探究圆的性质和相关定理（20分钟）老师通过PPT展示圆的性质和相关定理，如：圆的直径是半径的两倍、相交的两条弦相交于圆心等，并通过实例和证明帮助学生理解和掌握这些性质和定理。

Step 5：练习与应用（30分钟）老师设计一些练习题，让学生巩固和应用所学的知识。

其中包括计算圆的周长、面积，解决与圆相关的实际问题等。

Step 6：总结与展望（10分钟）老师总结本节课的重点内容，并展望下节课的内容。

五、作业设计：1.完成课堂上练习的剩余题目。

2.自行寻找生活中的圆形物体，并写下物体的名称和相关尺寸数据（如半径、直径等）。

3.提出一个与圆相关的问题，并编写解决方法和过程。

六、教学反思：本次课程设计注重学生的参与和实践，通过引导学生观察现象、探究规律、解决问题，培养学生的自主学习和解决问题的能力。

同时，通过运用PPT和实例，使抽象的知识更加形象具体，有助于学生的理解和记忆。

注意事项：1．答题前填写好自己的姓名、班级、考号等信息； 2．请将答案正确填写在答题卡上 第I 卷（选择题） 一、选择题 1.圆的直径有( )条． A ．1 B ．2 C ．4 D ．无数 2.下列说法正确的个数是( ) (1)圆的周长总是它直径的 3.14倍； (2)4比5少20%，也可以说5比4多20%； (3)正方体的棱长扩大3倍，体积就扩大9倍； (4)分数除以整数，等于分数乘以这个整数的倒数． A ．0个 B ．1个 C ．2个 D ．3个 3.在下面关于直径的说法中，①通过圆心的线段；②两端都在圆上的线段；③圆内最长的直线；④圆的任意一条对称轴；⑤任意两条半径相连；⑥周长与圆周率的比值；⑦顶点在圆上的直角三角形的斜边；正确的个数有( ) A ．2个 B ．3个 C ．4个 D ．5个 4.下列说法正确的个数是( ) ①圆的直径是半径的2倍 ②一个半圆形的周长等于同等半径圆周长的一半 ③甲数比乙数大13，乙数比甲数小14 ④等腰三角形的一个角是45°，这个三角形一定是等腰直角三角形． ⑤设a=1×2×3×…×29×30，则a 的末尾有8个0． A ．1个 B ．2个 C ．3个 D ．4个 5.在一个长10厘米、宽6厘米的长方形里画一个最大的半圆，这个半圆的直径是( )厘米． A ．10 B ．6 C ．3 D ．5 第Ⅱ卷（非选择题） 二、填空题 ______． 7.圆的半径扩大5倍，直径也扩大5倍．______．(判断对错) 8.用圆规画一个直径为4厘米的圆，圆规两脚间的距离应取______厘米，所画圆的面积是______平方厘米． 9.圆的大小与圆心无关，与半径的长短有关．______．(判断对错)…………订…………○…_班级：___________考号：___________…………订…………○…12.在一个长1Ocm 、宽6cm 的长方形中画一个最大的圆，这个圆的直径长______cm ． 13.把圆规的两脚分开，使两脚的距离是4cm ，这样画出的圆的半径是______，直径是______． 14.画圆时，圆规两脚叉开的距离就是所画圆的______；画出的周长是这个圆的直径的______倍． 15.填一填． (1)在下面各圆中，用红色笔描出直径，用蓝色笔描出半径，并量出它们的长度． (2)从______到______任意一点的线段叫做半径，同一个圆中半径有______条． (3)通过______并且______都在______的线段叫做直径，在同一个圆中直径是半径的______，半径是直径的______． (4)用圆规画一个直径为10厘米的圆，圆规两脚之间的距离是______厘米． 三、解答题 17.(0分)d=6厘米(画两条相互垂直的直径，连接圆上四点能够得到什么图形？) 18.(0分)计算． (1)求下列各圆的直径． r=54cm r =0.56dm (2)求下列各圆的半径． d=3.5m d=0.38dm ． 19.(0分)上体育课时，体育老师在讲动作要领时，经常让同学们围一个多半圆圈，请你利用所学知识分析一个其中的道理． 20.(0分)在一个圆中画有一条线段，怎样可以判断这条线段是否是所在圆的半径？(至少写出两种方法)参考答案1.解：由分析知：圆有无数条直径所以选：D2.解：(1)圆的周长总是它直径的3.14倍，说法错误，因为圆的周长总是它直径的π倍(2)4比5少：(5-4)÷5=20%，也可以说5比4多：(5-4)÷4=25%，所以本选项错误(3)正方体的棱长扩大3倍，依据正方体的体积=a 3，所以体积就扩大27倍，所以本选项错误(4)分数除以整数，等于分数乘以这个整数的倒数，应注意除数不能为0，即0除外，所以本选项错误 所以选：A3.解：依据直径的含义及特征知：①、②、③、④、⑤说法错误正确的有⑥、⑦两个所以选：A4.解：①圆的直径是半径的2倍，说法错误，前提是：在同圆或等圆中②一个半圆形的周长等于同等半径圆周长的一半，说法错误，半圆的周长多出了一条直径③甲数比乙数大13，假设乙数是3，则甲数是4，则乙数比甲数小14，说法正确④等腰三角形的一个角是45°，此角若是底角，则另一个底角也是45°，则最大角是90°，这个三角形一定是等腰直角三角形；45°的角若是顶角，则一个底角就是(180°-45°)÷2=67.5°，所以说法错误 ⑤设a=1×2×3×…×29×30，在中间有5、10、15、20、25、30共6个数除了25两个数含有2个因数5外，其它只有1个，所以一共有6+1=7个，则a 的末尾有7个0，所以本选项说法错误所以选：A5.解：在一个长10厘米、宽6厘米的长方形里画一个最大的半圆，这个半圆的直径是10厘米所以选：A6.解：依据圆周率的含义可知：圆周率π是一个无限不循环小数所以答案是：无限不循环小数7.解：假设出原来圆的半径是r ，则后来圆的半径是5r则直径扩大：(5r×2)÷(2r)=(10r)÷(2r)=5所以答案是：√8.解：4÷2=2(厘米)面积：3.14×22=12.56(平方厘米)答：圆规两脚间的距离应取2厘米，所画圆的面积是12.56平方厘米所以答案是：2，12.569.解：由分析可知：圆的大小与圆心无关，与半径的长短有关所以答案是：√10.解：圆周率的大小与圆的大小无关，圆的周长变大，圆的直径就变大，但圆周率不变所以一个圆的周长越大，圆周率越大，说法错误所以答案是：错误11.解：由分析可知：在一个长6cm 、宽4cm 的长方形中画一个最大的圆，这个圆的直径长4厘米 所以答案是：412.解：由分析可知：在一个长1Ocm、宽6cm的长方形中画一个最大的圆，这个圆的直径长6厘米所以答案是：613.解：把圆规的两脚分开，使两脚的距离是4cm，这样画出的圆的半径是4厘米，直径是8厘米所以答案是：4厘米，8厘米14.解：画圆时，圆规两脚叉开的距离就是所画圆的半径；画出的周长是这个圆的直径π倍所以答案是：半径，π15.解：(1)如图(2)从圆心到圆上任意一点的线段叫做半径，同一个圆中半径有无数条(3)通过圆心并且两端都在圆上的线段叫做直径，在同一个圆中直径是半径的2倍，半径是直径的一半(4)用圆规画一个直径为10厘米的圆，圆规两脚之间的距离是10÷2=5(厘米)所以答案是：圆心，圆上，无数；圆心，两端，圆上，2倍，一半；516.解：将一个圆形纸片最少要对折两次，才能找到两条折痕相交的那个点，即圆心把折痕延长即沿直径的直线就是对称轴17.解：6÷2=3(厘米)连接圆上4点即可得出一个正方形18.解：(1)因为r=54所以d=2r=2×54(厘米)=52因为r=0.56dm所以d=2r=2×0.56=1.12(分米)(2)因为d=3.5m所以r=d÷2=3.5÷2=1.75(米)因为d=0.38dm所以r=d÷2=0.38÷2=0.19(分米)19.解：因为同圆中，所有的半径都相等，体育老师在讲动作要领时，让同学们围一个多半圆圈，老师站的位置正好是圆心的位置，老师和每个学生之间的距离都是半径，同圆中，所有半径的长度都相等，这样学生听得清楚20.解：圆的半径是从圆心到圆周上任意一点的线段方法①：把圆规的两脚放在线段的端点上，固定一端，看另一端旋转是否与圆重合方法②：这条线段从圆心出发，另一端是否在圆周上。

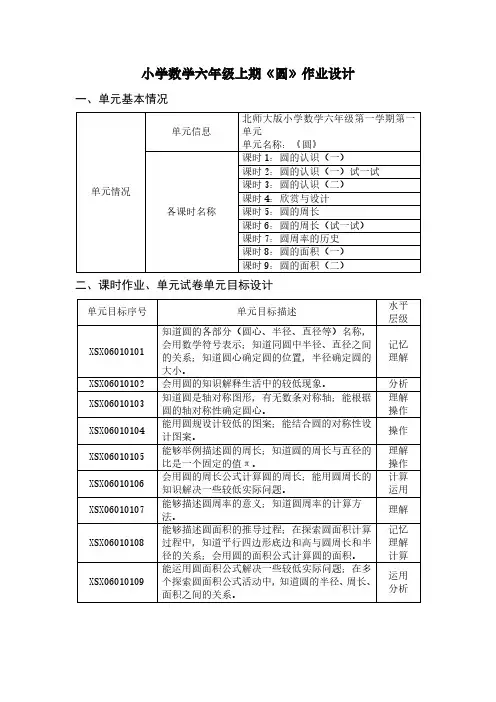
小学数学六年级上期《圆》作业设计一、单元基本情况单元情况单元信息北师大版小学数学六年级第一学期第一单元单元名称：《圆》各课时名称课时1：圆的认识（一）课时2：圆的认识（一）试一试课时3：圆的认识（二）课时4：欣赏与设计课时5：圆的周长课时6：圆的周长（试一试）课时7：圆周率的历史课时8：圆的面积（一）课时9：圆的面积（二）二、课时作业、单元试卷单元目标设计单元目标序号单元目标描述水平层级XSX06010101知道圆的各部分（圆心、半径、直径等）名称，会用数学符号表示；知道同圆中半径、直径之间的关系；知道圆心确定圆的位置，半径确定圆的大小。

记忆理解XSX06010102会用圆的知识解释生活中的较低现象。

分析XSX06010103知道圆是轴对称图形，有无数条对称轴；能根据圆的轴对称性确定圆心。

理解操作XSX06010104能用圆规设计较低的图案；能结合圆的对称性设计图案。

操作XSX06010105能够举例描述圆的周长；知道圆的周长与直径的比是一个固定的值π。

理解操作XSX06010106会用圆的周长公式计算圆的周长；能用圆周长的知识解决一些较低实际问题。

计算运用XSX06010107能够描述圆周率的意义；知道圆周率的计算方法。

理解XSX06010108能够描述圆面积的推导过程；在探索圆面积计算过程中，知道平行四边形底边和高与圆周长和半径的关系；会用圆的面积公式计算圆的面积。

记忆理解计算XSX06010109能运用圆面积公式解决一些较低实际问题；在多个探索圆面积公式活动中，知道圆的半径、周长、面积之间的关系。

运用分析三、课时作业、单元试卷题目属性统计分析（一）课时作业题目属性统计1.课时作业题目属性汇总表题目序号对应单元目标序号题目类型题目难度水平层级预计完成时间（分钟）题目来源Z0101XSX06010101填空低记忆2改编Z0102XSX06010101填空较低理解3改编Z0103XSX06010101填空较低理解4改编Z0104XSX06010101填空较低记忆4改编Z0105XSX06010101填空低记忆5改编Z0106XSX06010101填空、画图较低记忆3改编Z0107XSX06010101选择中等理解4改编Z0108XSX06010101解答较高分析6改编Z0201XSX06010102选择低记忆2改编Z0202XSX06010102选择低理解2改编Z0203XSX06010102选择低理解2改编Z0204XSX06010102解决中等理解4改编Z0301XSX06010103选择低理解2改编Z0302XSX06010103填空较低分析4改编Z0303XSX06010103选择低记忆2改编Z0304XSX06010103选择较低理解4改编Z0305XSX06010103画图较低理解5改编Z0306XSX06010103填空中等分析5改编Z0307XSX06010103填空中等分析6改编Z0401XSX06010104填空中等分析6改编Z0402XSX06010104画图较低创造5改编Z0403XSX06010104画图较低创造5改编Z0404XSX06010104画图较低创造5改编Z0405XSX06010104画图中等创造5改编Z0406XSX06010104画图中等创造5改编Z0501XSX06010105选择较低记忆2改编Z0502XSX06010105选择较低理解2改编Z0503XSX06010105选择中等理解4改编Z0504XSX06010105填空较低计算5改编Z0505XSX06010105选择中等理解3改编Z0506XSX06010105选择中等理解3改编Z0507XSX06010105填空较低记忆3改编Z0508XSX06010105选择较低记忆3改编Z0601XSX06010106填空较低理解3改编Z0602XSX06010106选择中等计算4改编Z0603XSX06010106计算较低计算6改编Z0604XSX06010106填空较低计算4改编Z0605XSX06010106解答中等分析、运用6原创Z0606XSX06010106解答中等计算6改编Z0607XSX06010106解答中等计算、运用5改编Z0608XSX06010106解答中等计算、运用6改编Z0701XSX06010107填空较低记忆1改编Z0702XSX06010107填空较低记忆1改编Z0703XSX06010107填空较低记忆1改编Z0704XSX06010107填空较低记忆2改编Z0705XSX06010107填空较低理解3改编Z0706XSX06010107解答中等计算4改编Z0707XSX06010107选择中等分析、计算3改编Z0801XSX06010108填空较低记忆2改编Z0802XSX06010108填空较低记忆1改编Z0803XSX06010108填空中等分析3改编Z0804XSX06010108填空较低计算2改编Z0805XSX06010108填空较低记忆2改编Z0806XSX06010108填空较低计算3改编Z0807XSX06010108选择中等分析3改编Z0808XSX06010108解答中等分析、计算4改编Z0901XSX06010109解答较低计算、运用2改编Z0902XSX06010109解答较低计算、运用2改编Z0903XSX06010109解答中等计算、运用4改编Z0904XSX06010109计算中等计算6改编Z0905XSX06010109解答中等计算4改编Z0906XSX06010109解答中等计算、运用4改编Z0907XSX06010109解答中等计算、运用4改编Z0908XSX06010109解答中等计算5改编2.课时作业题目属性统计表不同课时题量不同单元目标题量不同水平层级题量不同题目类型数量不同题目难度数量不同题目来源数量预计完成总时间（分钟）课时题量单元目标题量水平层级题量题型数量难度题量来源题量018XSX060101018记忆16选择16低37改编63231分024XSX060101024理解15填空25较低30原创1037XSX060101037分析10画图7中等26046XSX060101046计算20计算22较高1058XSX060101058运用8解答14068XSX060101068创造5077XSX060101077088XSX060101088098XSX060101098（二）单元试卷题目属性统计1.单元试卷题目属性汇总表题目序号对应单元目标序号题目类型题目难度水平层级预计完成时间（分钟）题目来源S0001XSX06010101填空题较低记忆1分改编S0002XSX06010109填空题较低计算2分改编S0003XSX06010103填空题较低记忆1分改编S0004XSX06010106填空题中等计算3分改编S0005XSX06010109填空题中等理解2分改编S0006XSX06010109填空题较高计算4分改编S0007XSX06010106XSX06010108填空题中等计算3分改编S0008XSX06010109填空题中等计算3分改编S0009XSX06010101判断题较低理解1分改编S0010XSX06010101判断题较低理解1分改编S0011XSX06010105判断题较低记忆1分改编S0012XSX06010103判断题较低理解1分改编S0013XSX06010109判断题中等理解1分改编S0014XSX06010102选择题较低理解1分改编S0015XSX06010105选择题较低理解1分改编S0016XSX06010109选择题中等分析2分改编S0017XSX06010106选择题中等计算2分改编S0018XSX06010106选择题较高计算3分改编S0019XSX06010108计算题中等计算3分改编S0020XSX06010108计算题中等计算3分改编S0021XSX06010101思考操作中等理解2分改编S0022XSX06010103思考操作中等理解3分改编S0023XSX06010106解答题较低计算5分改编XSX06010108S0024XSX06010108解答题中等计算5分改编S0025XSX06010109解答题中等分析5分改编S0026XSX06010106解答题中等计算5分改编S0027XSX06010109解答题较高计算5分改编S0028XSX06010106XSX06010109解答题较高计算运用10分改编2.单元试卷题目属性统计表不同单元目标题量不同水平层级题量不同题目类型数量不同题目难度数量不同题目来源数量预计完成总时间（分钟）单元目标题量水平层级题量题型数量难度题量来源题量XSX060101014记忆3填空8较低10改编2879 XSX060101021理解9判断5中等14XSX060101033分析2选择5较高4XSX060101040计算16思考操作2XSX060101052运用1解答题6XSX060101067XSX06010107XSX060101085XSX060101099四、课时作业[第一课时]1.1.1圆的认识（一）Z0101：直径是10分米的圆，半径是（）厘米。

圆的认识（一）
课前预习：
一、想一想、说一说
1.说一说生活中哪些地方可以看到圆形
2、出示不同的圆形物体，说一说这些图形与学过的图形比有什么不同
课堂训练：
一、填空。

1．圆中心的一点叫做（），用字母（）表示，它到圆上任意一点的距离都（）。

2．（）叫做半径，用字母（）表示。

3．（）叫做直径，用字母（）表示。

4．在一个圆里，有（）条半径、有（）条直径。

5．（）确定圆的位置，（）确定圆的大小。

6．画圆时，圆规两脚间的距离是圆的( )。

二、做图题
画一个半径为2厘米的圆，标出它的一条直径、一条半径和圆心，并分别用字母表示。

能力巩固：
一、想一想、做一做
1、完成课本第三页中的“画一画”和“想一想”。

2、分组讨论“圆的位置与什么有关系“和”圆的大小与什么有关系“
3、画三个相等的圆。

拓展延伸：
请同学们练习使用圆规，自己画圆并指出圆心，写出半径的长度。

一个关于圆的项目化作业示例项目名称：制作一个圆形纸板钟表项目背景：在这个项目中，您将使用一张圆形纸板和一些其他材料来制作一个简单的纸板钟表。

这个钟表将包括表盘、时针、分针和秒针，并且能够显示时间。

通过完成这个项目，您将了解圆的性质、钟表的构造和时间的基本概念。

项目目标：1.掌握圆的性质和特征，了解如何制作一个准确的圆形纸板。

2.学习钟表的构造和工作原理，了解时针、分针和秒针的运动规律。

3.掌握基本的绘画和手工技能，能够制作出精美的纸板钟表。

4.培养观察力和耐心，提高动手能力。

项目实施步骤：1.准备材料：一张圆形纸板、水彩笔、铅笔、橡皮、细长纸条、剪刀、胶水等。

2.在圆形纸板上绘制钟表的表盘，包括12个等分的刻度和时针、分针、秒针的位置。

可以使用水彩笔或铅笔进行绘制，注意保持线条清晰。

3.根据需要，在表盘上添加其他元素，如数字、图案等。

可以使用不同的颜色和线条来装饰表盘，使其更加美观。

4.用细长纸条制作时针、分针和秒针。

在纸条的一端绘制指针的形状，并使用剪刀剪下来。

注意指针的长度应该与纸板的半径相匹配。

5.将制作好的时针、分针和秒针粘贴到纸板上相应的位置。

使用胶水将指针粘贴牢固。

6.测试纸板钟表的功能。

轻轻旋转纸板，观察时针、分针和秒针是否能够正常转动，并且显示的时间是否准确。

7.如果需要，可以对纸板钟表进行进一步的美化和装饰，使其更加精美。

项目总结：通过这个项目化作业，您将了解圆的性质和特征，掌握钟表的构造和工作原理，同时培养了基本的绘画和手工技能。

通过完成这个项目，您将获得更多的实践经验，提高自己的动手能力和创造力。

圆的性质辅导教案学生姓名性别年级九年级学科数学授课教师上课时间第（）次课共（）次课课时：3课时科组长签名教学主任签名教学课题圆的性质教学目标熟悉圆的基本概念与性质学会运用性质解决基本题目教学重点与难点圆周角定理的应用一、知识点讲解考点1 圆的有关概念圆的定义定义1：在一个平面内，一条线段绕着它固定的一个端点旋转一周，另一个端点所形成的图形叫做圆.定义2：圆是到定点的距离①定长的所有点组成的图形.弦连接圆上任意两点的②叫做弦.直径直径是经过圆心的③，是圆内最④的弦.弧圆上任意两点间的部分叫做弧，弧有⑤之分，能够完全重合的弧叫做⑥.等圆能够重合的两个圆叫做等圆.同心圆圆心相同的圆叫做同心圆.考点2 圆的对称性圆的对称性圆是轴对称图形，其对称轴是任意一条经过⑦的直线.圆是中心对称图形，对称中心为⑧.垂径定理定理垂直于弦的直径⑨弦，并且平分弦所对的两条⑩.推论平分弦(不是直径)的直径⑪弦，并且⑫弦所对的两条弧.圆心角、弧、弦之间的关系在同圆或等圆中，如果两个圆心角﹑两条弧或两条弦中有一组量⑬，那么它们所对应的其余各组量也分别相等.考点3 圆周角圆周角的定义顶点在圆上，并且⑭都和圆相交的角叫做圆周角.圆周角定理一条弧所对的圆周角等于它所对的圆心角的⑮.推论1 同弧或等弧所对的圆周角⑯.推论2 半圆(或直径)所对的圆周角是○17；90°的圆周角所对的弦是○18.推论3 圆内接四边形的对角○19.考点解读【易错提示】由于圆中一条弦对两条弧以及圆内的两条平行弦可以在圆心的同侧和异侧两种情况，所以利用垂径定理计算时，有时要分情况讨论，不要漏解.1.注意在同圆或等圆中，弦、弧、圆心角和圆周角等量关系的互相转化；利用垂径定理进行计算或证明，通常利用半径、弦心距和弦的一半组成直角三角形求解.2.圆的性质的综合运用，要善于挖掘题中的隐含条件.二、重点题型讲解命题点1 圆的有关概念例1 下列说法中，正确的是( )A.直径是弦B.弧是半圆C.长度相等的弧是等弧D.弦是圆上两点间的部分方法归纳：解答这类试题的关键是结合图形理解圆的有关概念的内涵.1.如图，MN为⊙O的弦，∠M=30°，则∠MON等于( )A.30°B.60°C.90°D.120°2.下列说法中，结论错误的是( )A.直径相等的两个圆是等圆x k b 1B.长度相等的两条弧是等弧C.圆中最长的弦是直径D.一条弦把圆分成两条弧，这两条弧可能是等弧3.到定点O的距离为3 cm的点的集合是以点为圆心，为半径的圆. 命题点2 垂径定理例2 如图，AB为⊙O的直径，CD⊥AB，若AB=10，CD=8，求圆心O到弦CD的距离.【思路点拨】连接OC，由AB=10得出OC的长，再根据垂径定理求出CE的长，根据勾股定理求出OE即可.【解答】方法归纳：利用垂径定理进行计算或证明时，通常利用半径、弦心距和弦的一半组成直角三角形求解.1.如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为( )A.2B.4C.6D.82.如图，在⊙O中，已知半径为5，弦AB的长为8，那么圆心O到AB的距离为.3.如图AB是⊙O的直径，∠BAC=42°，点D是弦AC的中点，则∠DOC的度数是.4.如图，已知AB是⊙O的弦，点C在线段AB上，OC=AC=4，CB=8.求⊙O的半径.命题点3 圆心角、弧、弦之间的关系例3 如图，在⊙O中，AB= AC，∠A＝30°，则∠B＝( )A.150°B.75°C.60°D.15°方法归纳：在求圆中角的度数时，通常要利用圆周角、圆心角、弧、弦之间的关系进行求解.1.如图，已知AB是⊙O的直径，C、D是BE上的三等分点，∠AOE=60°，则∠COE是( )A.40°B.60°C.80°D.120°2.如图，AB是⊙O的直径，四边形ABCD内接于⊙O，若BC=CD=DA=4 cm，则⊙O的周长为( )A.5πcmB.6πcmC.9πcmD.8πcm3.如图，在⊙O中，点C是弧AB的中点，∠A=50°，则∠BOC等于度.4.如图，在⊙O中，CD为⊙O的直径，AC=BC，点E为OD上任意一点(不与O、D重合).求证：AE=BE.命题点4 圆周角定理例4 如图，AB是⊙O的直径，∠AOC=110°，则∠D=( )A.25°B.35°C.55°D.70°【思路点拨】因为AB是直径，所以∠BDA=90°，再根据同弧所对的圆心角与圆周角之间的关系可求得∠ADC的度数.方法归纳：在圆中，出现直径时，一般都联想到直径所对的圆周角是直角.圆周角与圆心角之间的转化也是解决问题的关键点.1.如图，⊙O是△ABC的外接圆，连接OA、OB，∠OBA=50°，则∠C的度数为( )A.30°B.40°C.50°D.80°2.从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是( )3.如图，AB为⊙O直径，CD为⊙O的弦，∠ACD=25°，∠BAD的度数为.4.如图，⊙O是△ABC的外接圆，点D为AC上一点，∠ABC=∠BDC=60°，AC=3 cm，求△ABC的周长.三、课堂小测1.下列四个图中，∠x是圆周角的是( )2.如图，已知AB是△ABC外接圆的直径，∠A=35°，则∠B的度数是( )A.35°B.45°C.55°D.65°3.下列四个命题：①等边三角形是中心对称图形；②在同圆或等圆中，相等的弦所对的圆周角相等；③三角形有且只有一个外接圆；④垂直于弦的直径平分弦所对的两条弧.其中真命题的个数有( )A.1个B.2个C.3个D.4个4.如图，线段AB是⊙O的直径，弦CD⊥AB，∠CAB=20°，则∠AOD等于( )A.160°B.150°C.140°D.120°5.绍兴是著名的桥乡，如图，圆拱桥的拱顶到水面的距离CD为8 m，桥拱半径OC为5 m，则水面宽AB为( )A.4 mB.5 mC.6 mD.8 m6.如图，⊙O是△ABC的外接圆，∠AOB＝60°，AB＝AC＝2，则弦BC的长为( )A.3B.3C.23D.47.如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是( )A.30°B.45°C.60°D.70°8.如图，CD是⊙O的直径，弦AB⊥CD于E，连接BC、BD，下列结论中不一定正确的是( )A.AE=BEB.AD=BDC.OE=DED.∠DBC=90°9.如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为( )A.95B.245C.185D.5210.如图，已知三点A、B、C都在⊙O上，∠AOB=60°，∠ACB= .11.在⊙O中，已知半径长为3，弦AB长为4，那么圆心O到AB的距离为.12.如图，AB为⊙O直径，点C、D在⊙O上，已知∠BOC=70°，AD∥OC，则∠AOD= .13.如图，水平放置的圆柱形排水管道的截面直径是1 m，其中水面的宽AB为0.8 m，则排水管内水的深度为.14.如图，A、B、C是⊙O上的三点，∠CAO=25°，∠BCO=35°，则∠AOB= .15.如图，AB、CD是⊙O的弦，AB⊥CD，BE是⊙O的直径.若AC=3，则DE= .16.如图，□ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，∠ADC=54°，连接AE，求∠AEB的度数.17.已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D.如图，若BC为⊙O的直径，AB＝6，求AC，BD,CD的长.18.如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E.(1)若∠B=70°，求∠CAD的度数；(2)若AB=4，AC=3，求DE的长.19.如图，已知点A，B，C在⊙O上, ACB为优弧，下列选项中与∠AOB相等的是( )A.2∠CB.4∠BC.4∠AD.∠B+∠C20.如图，点P是等边三角形ABC外接圆⊙O上的动点，在以下判断中，不正确的是( )A.当弦PB最长时，△APC是等腰三角形B.当△APC是等腰三角形时，PO⊥ACC.当PO⊥AC时，∠ACP=30°D.当∠ACP=30°时，△BCP是直角三角形21.如图，半径为6 cm的⊙O中，C、D为直径AB的三等分点，点E、F分别在AB两侧的半圆上，∠BCE=∠BDF=60°，连接AE、BF，则图中两个阴影部分的面积为cm2.22.在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连接CD.(1)如图1，若点D与圆心O重合，AC＝2，求⊙O半径r；(2)如图2，若点D与圆心O不重合，∠BAC＝25°，请直接写出∠DCA的度数.四、课后作业1．圆内接五边形各边相等，各边所对的圆心角的度数是．，∠B=70°，则∠C= ．2．如图1，在⊙O中，AB AC3．在半径为2的⊙O中，弦AB的长为22，则弦AB所对的圆心角∠AOB的度数是．4．若⊙O是△ABC的外接圆，OD⊥BC于D，且∠BOD=48°，则∠BAC= ．5．如图2所示，弦AB过圆心O，∠A=30°，⊙O的半径长为23，弦CD⊥AB于E，则CD 的长为．D. 4＜OM＜5。

圆的跨学科作业设计一、数学中的圆1. 回顾圆的基本定义、性质和公式，如周长、面积、半径等。

2. 探讨圆与其他几何图形的关系，如圆与椭圆、圆与直线等。

3. 研究圆的对称性，包括中心对称、轴对称和旋转对称。

4. 探讨圆在解析几何中的应用，如极坐标、参数方程等。

二、物理中的圆1. 探讨匀速圆周运动的基本公式和物理意义，如角速度、线速度、周期等。

2. 研究离心运动及其在日常生活中的应用。

3. 探讨圆周运动中的向心力和离心力，以及它们在物体运动中的作用。

4. 了解圆周运动在机械、电力和磁力等领域的应用。

三、化学中的圆1. 了解原子结构模型中的电子云分布和原子轨道形状，以及它们的物理意义。

2. 研究化学键中的共价键和离子键的形成机制，以及它们对物质性质的影响。

3. 探讨有机化学中的环状化合物及其形成条件。

4. 了解分子轨道理论在化学中的应用，如分子光谱和化学反应机理。

四、地理中的圆1. 了解地球的形状和大小，以及地球测量学的基本概念。

2. 研究经纬度的概念及其在地理定位中的应用。

3. 探讨地球的自转和公转对地球表面自然现象的影响，如昼夜交替和季节变化。

4. 研究地图投影的方法和原理，以及其在地图制作和导航中的应用。

五、历史中的圆1. 了解古代文明中圆的应用和发展，如古代数学家对圆的探索和研究。

2. 探讨圆在古代建筑和艺术中的应用，如圆形建筑和圆形雕塑等。

3. 研究近代科学和技术中圆的应用和发展，如圆周运动在机械和电力等领域的应用。

4. 了解现代科技中圆的最新应用和发展趋势，如圆周率在计算机科学和信息技术等领域的应用。

六、艺术中的圆1. 了解圆形在绘画和雕塑艺术中的应用，如圆形构图和圆形造型等。

2. 研究圆形在建筑艺术中的应用，如圆形建筑和穹顶等。

3. 探讨圆形在音乐艺术中的应用，如圆形旋律和圆形节奏等。

4. 了解圆形在其他艺术形式中的应用，如文学、电影和戏剧等。

七、技术中的圆1. 研究圆在机械制造中的应用，如车轮、齿轮和轴承等的设计和应用。

d.应用圆的周长和面积公式解决实际问题，如计算操场跑道长度、草坪面积等。
e.掌握圆的扇形概念，绘制并计算扇形的面积。
f.分析生活中与圆相关的实例，体会圆在实际应用中的价值。
二、核心素养目标
《圆》单元设计作业核心素养目标：
1.培养学生的几何直观与空间想象能力，通过绘制圆和扇形，加深对圆的基本概念和性质的理解。
五、教学反思
在这次《圆》单元的教学中，我发现学生们对于圆的基本概念和性质掌握得相对较好，但还是在一些地方遇到了困难。首先，圆周长和面积公式的推导过程中，部分学生对于圆周率π的理解不够深入，导致在计算时出现错误。为此，我通过引入实际案例，让学生们观察和测量，帮助他们更好地理解π的意义。
另外，对于扇形面积的计算，学生们普遍觉得有些抽象。针对这一情况，我设计了一个简单的实验操作，让学生们亲自绘制扇形，并计算其面积。这样，他们就能更直观地理解扇形与圆心角的关系。
《圆》单元设计作业（作业设计）
一、教学内容
《圆》单元设计作业（作业设计）：
1.教材章节：《圆的认识》、《圆的性质》、《圆的周长与面积》、《圆与扇形》。
2.作业内容：
a.解释圆的基本概念，绘制不同半径的圆。
b.利用实例说明圆的性质，如半径相等、直径垂直等。
c.计算给定圆的周长和面积，并讨论其与半径、直径的关系。
-教学策略：设计生活情境，让学生观察和讨论圆在现实世界中的应用，如车轮的滚动、圆形建筑的设计等。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《圆》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过圆形物体？”（如车轮、硬币等）。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索圆的奥秘。

圆的跨学科作业设计摘要：1.引言：介绍圆的跨学科作业设计的意义和目的2.圆的数学概念：解释圆的定义和性质3.圆的艺术设计：探讨圆在艺术领域的应用4.圆的工程应用：分析圆在工程设计中的实例5.圆的科学研究：讨论圆在科学领域的重要性6.圆的社会科学应用：举例说明圆在社会科学领域的作用7.结论：总结圆的跨学科作业设计的重要性和价值正文：【引言】在当今高度融合的多学科世界中，跨学科作业设计成为了教育领域的一大趋势。

将不同学科的知识融合在一起，可以提高学生的综合素质，培养创新型人才。

本文将以圆为主题，探讨其在不同学科领域的应用，从而设计一份跨学科作业。

【圆的数学概念】圆，是平面上到一个固定点的距离等于定长的所有点的集合。

这个固定点被称为圆心，定长被称为半径。

圆具有许多重要的性质，如对称性、圆周角、圆的面积和周长等。

在数学领域，研究圆的相关性质和应用是几何学的重要组成部分。

【圆的艺术设计】在艺术领域，圆作为一个基本的几何形状，具有丰富的表现力和美学价值。

艺术家们可以利用圆的简约、和谐、对称等特点，创作出各种精美的艺术品。

例如，古代的太极图就是一个典型的圆的图形，它象征着宇宙间阴阳两极的和谐统一。

【圆的工程应用】在工程设计领域，圆的应用无处不在。

例如，汽车轮胎的设计就是典型的圆形应用，它既能保证行驶的稳定性，又能有效降低摩擦力，提高行驶效率。

此外，建筑领域中的穹顶设计也是圆的应用之一，如悉尼歌剧院等著名建筑，都采用了圆形穹顶设计，既美观又实用。

【圆的科学研究】在科学领域，圆同样具有重要的意义。

例如，在物理学中，圆可以用来描述粒子的运动轨迹；在化学中，圆可以表示分子结构；在生物学中，细胞核的结构也是圆形的。

这些都充分体现了圆在科学研究中的重要性。

【圆的社会科学应用】在社会科学领域，圆同样具有广泛的应用。

例如，在心理学中，可以利用圆来描述人际关系的亲密程度；在管理学中，圆可以表示组织的结构和层次关系。

这些都充分体现了圆在社会科学领域的重要性。

《圆周运动》作业设计方案（第一课时）一、作业目标通过本次作业，学生应掌握圆周运动的基本概念和原理，理解向心力的计算方法，并能应用相关知识解决实际问题。

二、作业内容1. 基础知识测试(1)写出圆周运动的概念，并解释其基本特征。

(2)简述向心力的定义，并说明其在圆周运动中的作用。

(3)举例说明生活中常见的圆周运动现象。

(4)请用公式描述圆周运动中的向心力，并说明其物理意义。

2. 实践性作业(1)制作简易圆形轨道：学生需使用废弃的纸杯、回形针、胶带等材料，制作一个简易圆形轨道。

要求能够保持轨道稳定，并在轨道上稳定放置一个小重物。

(2)圆周运动实验：使用提供的实验器材（如小球、线、支架等），进行圆周运动实验。

要求记录实验过程、小球的运动轨迹、向心力的大小等数据，并分析实验结果。

3. 综合性问题解答请学生分析并解答以下圆周运动问题：(1)一个质量为m的小球在水平面上做匀速圆周运动，转动半径为r，角速度为ω，求小球受到的向心力大小。

(2)一个质量为m的小车在固定轨道的圆弧部分做圆周运动，圆弧的半径为R，小车在最高点时的速度为v，求此时小车对轨道的压力大小。

三、作业要求1. 独立完成作业：学生需独立完成本次作业，不得抄袭或依赖他人。

2. 认真阅读教材：学生在完成作业的过程中，应认真阅读教材及相关资料，确保对问题的理解和解答的正确性。

3. 实践操作：对于实践性作业，学生应按照要求进行操作和记录，确保数据的准确性和真实性。

4. 按时提交：学生应在规定时间内提交作业，以便教师及时评价和反馈。

四、作业评价1. 评价标准：根据学生提交的作业情况，结合教材中的知识点和问题解答的正确性，给予相应的评价。

2. 评价方式：教师评价为主，结合学生互评和自我评价的方式，综合评估学生的作业完成情况。

五、作业反馈1. 反馈形式：教师将在批改完作业后，以书面或口头形式向学生反馈作业评价结果，指出学生的优点和不足，提出改进建议。

2. 学生对反馈的响应：学生应认真听取教师的反馈，并根据建议进行改进和提升。

以下是一个圆单元作业设计案例，旨在帮助学生巩固和应用对圆的相关概念和技能：
作业名称：探索圆的性质
任务1：测量和计算圆的周长和面积
要求学生使用卷尺或尺子等工具测量给定的圆的直径，并计算出其周长和面积。

学生需要熟悉圆周率（π）的概念，以及计算圆的周长和面积的公式。

任务2：构造圆的切线和弦
学生需要绘制给定圆上的切线和弦。

他们将了解切线与弦的定义以及它们与圆的关系。

学生可以通过将圆分成不同的部分来观察弦的长度和角度变化。

任务3：解决实际问题
学生将面临一些实际问题，例如根据给定的圆形花坛的半径和面积，在规定的条件下计算需要多少土壤填充。

学生需要运用他们所学的圆的相关知识和推理能力来解决这些问题。

任务4：制作圆的艺术作品
学生被要求创作一个关于圆的艺术作品，可以是绘画、雕塑、拼贴等形式。

作品应该能够展现学生对圆的理解和创意，并能够与其他同学分享。

评估方式：
-周长和面积计算准确性和方法的使用。

-切线和弦的构造准确性和对关系的理解。

-实际问题的解决过程和答案的合理性。

-艺术作品的创意和表达力。

通过这个圆单元作业设计，学生将有机会运用他们所学的圆相关的知识和技能，从不同角度来理解和应用圆的性质。

同时，评估方式也可以促进学生的全面发展，包括计算能力、几何思维、问题解决和艺术创造力等方面。

第一章 《圆》的单元作业设计说明
一、作业设计指导思想
本单元作业设计考查学生对义务教育小学数学北师大版教材第 11 册第一单元《圆》 的相关学习内容掌握的情况。设计以 2022 版《义务教育数学课程标准》为基本指导思想， 遵循学生身心发展规律和学科学习规律以及双减政策的相关规定，以检验学生对本单元 基础知识、基本技能的掌握及核心素养的发展为设计重点，以“考查基础知识的同时注 重考查能力”为原则，力求促进对学生基本的数学概念的理解，对定理、法则及数学结 论的本质的应用，对蕴含的数学思想和方法的体会，从而实现提升综合运用所学知识分 析和解决实际问题的能力。真正做到落实作业整体育人的功能，切实做到让学生通过作 业练习达到巩固知识，提高能力，培养素质的目的。
单元作业设计的双向细目表
知识点的课 标要求
题号
作业内容
参考答案
主要考
数
查知识 设计意图
学
点
了理 掌 运 问
解解 握 用 题
提
出
圆的认识
时钟的分针转动一周形
一 1 成的图形是（ ）。
圆
理解圆的
圆的形 成
形成过 程，并与 生活建立
联系。
（
）确定圆的大
一2
小，（ 位置。
）确定圆的
半径；圆心
体会圆心 圆心和 和半径的 半径的 作用，确 作用 定决定圆
行
五1 车 车
6.16d m
轮
圆
形 桌
600mm
布
五2
出与圆有 关的组合 图形的对 称轴。
130mm;3.08dm; 1200mm
掌握同圆 同一个 中，半径 圆中半 与直径间 径和直 的关系， 径的关 能熟练转

《圆》课堂笔记
以下是整理的关于人教版六年级数学《圆》的课堂笔记：
一、圆的认识
1.圆的概念：圆是由曲线围成的封闭图形，它可以看作是所有到
定点（圆心）的距离等于定长（半径）的点的集合。

2.圆心：圆的中心点叫做圆心，用字母“O”表示。

3.半径：连接圆心和圆上任意一点的线段叫做半径，用字母“r”
表示。

4.直径：通过圆心且两个端点都在圆上的线段叫做直径，用字母“d”表示。

5.半径与直径的关系：在同一个圆中，直径是半径的2倍，即d=2r。

二、圆的周长
1.圆的周长的概念：圆的周长是围成圆的曲线的长度，用字母“C”
表示。

2.周长公式：圆的周长等于2π乘以半径，即C=2πr。

其中π
是一个特殊的数，约等于3.14159。

3.圆周率：圆的周长与直径的比值叫做圆周率，用字母“π”表示。

4.周长的推导公式：根据周长公式和圆的直径与半径的关系，可
以推导出周长公式C=πd或C=2πr。

三、圆的面积
1.圆的面积的概念：圆的面积是圆所占平面的大小，用字母“S”
表示。

2.面积公式：圆的面积等于π乘以半径的平方，即S=πr²。

3.面积的推导公式：根据面积公式和圆的半径与直径的关系，可
以推导出面积公式S=π(d/2)²或S=π(r²)。

4.圆的大小比较：两个圆的大小可以通过它们的半径或直径来比
较。

两个圆的半径相等时，它们的直径也相等；直径相等时，它们的半径也相等。

以上是关于人教版六年级数学《圆》的课堂笔记整理，希望对您有所帮助。

精选全文完整版（可编辑修改）附件12022年新密市中小学作业设计案例申报书案例名称《圆的认识》单元作业设计案例学段学科小学数学主持人完成单位一、基本信息表二、案例正文积变形”“极限”等数学思想方法，聚焦数学抽象、直观想象等数学核心素养，进一步发展问题解决的能力。

基于单元知识图谱，将这单元置于“图形与几何”领域，以“大观念”提炼单元核心素养。

《数学课程标准》指出：“图形与几何”领域的内容需从多角度刻画图形的特征、大小、运动和位置，发展学生空间观念和推理能力。

《站在巨人的肩膀上》一书中指出：分类、分析和表示是我们认识图形的主要工具。

基于以上认识，提炼如下《圆》单元的核心大观念：(三)整体教学流程透视将“圆”这个单元的学习放到小学六年的学习链中去分析，“圆”的学习，与以往平面图形的中学习有着显著的不同，它将从对直线图形的研究过渡到曲线图形的研究，无论是研究曲线图形的思想还是方法，对于学生而言都是一种跨越和挑战，因此，通过本单元的学习，不仅要让学生掌握圆的一些基础知识，还要让学生感受与体悟“化曲为直”、“等积变换”、“极限”等数学思想方法，以促进与发展学生的数学思维方法和问题解决的能力。

从整体视角分析:随着教学内容的推进，学生几何思维水平由低到高，逐渐向水平3--形式化演绎迈进。

单元整体教学活动的设计要依据思维水平发展的规律，帮助学生经历数学化。

但分析“圆”这个单元的教学内容，除了“圆的认识”和“扇形的认识”两节课，大多涉及的是单纯的计算或者作图，缺乏了对于圆的基本特征的深度理解和应用，不利于学生构建一个有意义的项目学习序列。

基础性作业：聚焦大观念“分类”，结合具体情境和作业探索，巩固圆和扇形的基本概念及特征；学会用圆规画圆；理解和掌握圆的周长和面积计算公式，并解决相应的实际问题，落实单元知识和技能。

探究性作业：聚焦大观念“分析”，经历尝试、探究、分析的过程，积累解决数学作业的经验，体会转化、极限等数学思想，发展数学抽象、直观想象等核心素养，感悟知识之间的联系。

5.1圆的认识（同步练习）一、选择题1．马路上大多数井盖的平面轮廓都采用圆形，这是应用了（）的特点。

A．圆是最美图形B．圆是曲线图形C．圆有无数条对称轴D．同一圆的直径都相等2．下列图形中，对称轴条数最多的是（）。

A．B．C．D．3．淘气用圆规画圆，他把圆规两脚之间的距离定为4cm，如图所示。

那么他画出的圆的直径是（）。

A．2cm B．4cm C．8cm D．12.56cm 4．如图，在以点O为圆心的圆内画出三角形OAB。

如果∠A＝60°，那么这个三角形一定是等边三角形。

做出这个判断是根据（）。

A．圆心决定圆的位置B．同一个圆内的半径都相等C．同一个圆内的直径是半径的2倍D．圆的周长是直径的π倍5．小宇坚持步行上学，他家离学校1km，表示小宇家与学校位置关系较合理的是（）。

1A．小宇家一定在图（1）中的M点。

B．小宇家一定在图（2）中的M或N点。

C．小宇家在图（3）中M、N、P、Q中的某一点。

D．小宇家可能在图（4）中以学校为圆心、半径为1km的圆周上的某一点。

二、填空题6．如图，在长方形中的两个圆大小相等，1O、2O分别是两个圆的圆心。

已知长方形的宽是4cm，这个长方形的长是( )cm。

7．一个圆的半径和直径的比是( )，比值是( )。

8．如图，将圆周分成12等份，那么，点A在点O的( )偏( )( )方向( )千米处。

9．下图中长方形的对角线AB的长度是( )cm。

210．圆的大小由( )决定，圆的对称轴有( )条。

三、解答题11．下图为2022年北京冬奥会奖牌——“同心”。

它的形象来源于中国古代同心圆玉壁，共设五环。

五环同心，同心归圆，表达了“天地合·人心同”的中华文化内涵，也象征着奥林匹克精神将世界人民聚集在一起，共享奥运荣光。

请用喜欢的方式说明你是如何找到“同心”奖牌所在圆的圆心。

12．下图是用杯子盖在纸上画出来的一个圆，如果剪下这个圆，你能找出它的圆心吗？请把你找圆心的过程或步骤写下来，也可以用示意图画画并说明思路。

圆的面积实践作业圆的面积是一个重要的几何概念，它在日常生活中有着广泛的应用。

无论是建筑设计、地理测量还是工程计算，我们都需要用到圆的面积来进行相关的计算和分析。

在数学上，圆的面积是通过半径的平方乘以π（pi）来计算的。

然而，在这篇文章中，我们将尽量避免使用数学公式或计算公式，以便更好地向读者解释圆的面积的概念。

让我们想象一个完美的圆形。

它没有任何边缘或尖角，是一个无限光滑的形状。

我们可以通过观察圆的周长来更好地理解圆的面积。

周长是指围绕圆形边缘的长度，也可以看作是圆形的边界。

现在，我们将面积与周长进行对比。

周长是一个一维的量，它只涉及到长度。

而面积是一个二维的量，它涉及到长度和宽度。

面积实际上是将周长延伸到了二维空间上，所以它代表了一个平面内的大小。

对于一个圆来说，它的面积是圆心到圆边界的距离的平方乘以π。

这个距离被称为半径。

半径是从圆心到圆的任意一点的距离，它是圆的重要属性之一。

半径的平方乘以π就是圆的面积。

圆的面积可以用来解决很多实际问题。

比如，在建筑设计中，我们可以使用圆的面积来计算圆形房间的地板面积。

在地理测量中，我们可以使用圆的面积来计算湖泊或河流的面积。

在工程计算中，圆的面积可以帮助我们计算管道或容器的容积。

总结一下，圆的面积是一个重要的几何概念，它可以通过半径的平方乘以π来计算。

虽然我们在这篇文章中避免使用数学公式或计算公式，但我们通过比较圆的周长和面积，以及解释半径的概念，希望能够更好地向读者解释圆的面积的概念和应用。

无论是在建筑设计、地理测量还是工程计算中，圆的面积都有着重要的作用。

希望通过这篇文章，读者能够更好地理解圆的面积，并将其应用到实际问题中。