逻辑推理用思维导图学数学

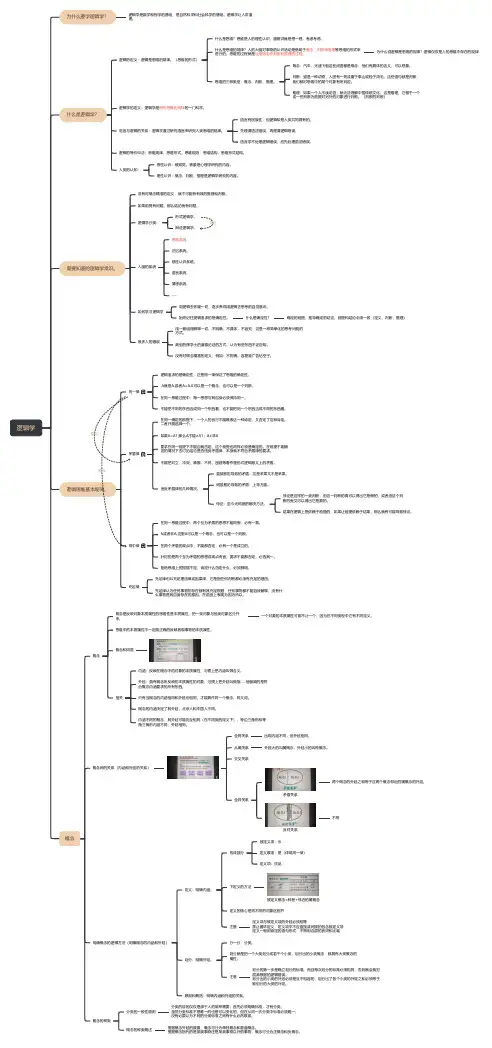
逻辑学为什么要学逻辑学？逻辑学是数学和哲学的基础，是自然科学和社会科学的基础。

逻辑学让人讲道理。

什么是逻辑学？逻辑的定义：逻辑是思维的规律。

（思维的形式）什么是思维？思维是人的理性认识，通常讲就是想一想，考虑考虑。

什么是思维的规律？人的大脑对事物的认识活动是借助于概念、判断和推理等思维的形式来进行的。

思维的过程就是运用概念作判断和推理的过程。

为什么说逻辑是思维的规律？逻辑仅仅是人的思维中存在的规律思维的三种类型：概念、判断、推理。

概念：汽车，光速飞船这些词语都是概念，他们有具体的含义，可以想象。

判断：猫是一种动物，人固有一死或重于泰山或轻于鸿毛，这些语句都是判断，他们都对思维中的某个对象有所判定。

推理：如果一个人不读论语，就无法理解中国传统文化，这是推理，它基于一个或一些判断为前提对另外的对象进行判断。

（判断的判断）逻辑学的定义：逻辑学是研究思维的规律的一门科学。

语言与逻辑的关系：逻辑学通过研究语言来研究人类思维的规律。

语言有民族性，但逻辑却是人类共同具有的。

先理清语法错误，再理清逻辑错误。

语言学不处理逻辑错误，应先处理语法错误。

逻辑的等价叫法：思维规律，思维形式，思维规则，思维结构，思维形式结构。

人类的认知：感性认识：感知觉、表象是心理学研究的内容。

理性认识：概念、判断、推理是逻辑学研究的内容。

需要知道的逻辑学常识。

没有对概念精准的定义，就不可能有有效的推理和判断。

如果前提有问题，那么结论就有问题。

逻辑学分类：形式逻辑学。

辩证逻辑学。

人脑的系统思维系统。

记忆系统。

感性认识系统。

语言系统。

情感系统。

......如何学习逻辑学用逻辑去怀疑一切，逐步养成用逻辑去思考的自觉意识。

始终记住逻辑追求的是确定性。

什么是确定性？确定的前提，推导确定的结论。

前提和结论必须一致（定义，判断，推理）很多人的错误用一套道理解释一切，不明确，不具体，不追究，这是一种简单化的思考问题的方式。

典型的儒学士的道德论证的方式，认为有些东西不证自明。

思维导图在高中数学复习教学中的应用高中数学知识体系庞大、逻辑性强，对于学生的思维能力和综合运用知识的能力要求较高。

在复习阶段，如何帮助学生系统地梳理知识、提高复习效率，是每一位数学教师面临的重要课题。

思维导图作为一种有效的思维工具，能够将抽象的数学知识以直观、形象的方式呈现出来，为高中数学复习教学提供了新的思路和方法。

一、思维导图的概念和特点思维导图是由英国心理学家托尼·博赞于 20 世纪 60 年代提出的一种图形思维工具。

它以一个中心主题为出发点，通过分支和线条将相关的知识点、概念、方法等连接起来，形成一个层次分明、结构清晰的知识网络。

思维导图具有以下几个特点：1、可视化思维导图将复杂的知识以图形的形式展现出来，使抽象的思维过程变得直观可见。

学生通过观察思维导图，可以快速把握知识的整体结构和内在联系，提高对知识的理解和记忆。

2、发散性思维导图鼓励从一个中心主题出发，进行多角度、多层次的思考和联想。

这种发散性思维能够帮助学生开拓思路，发现知识之间的新联系，培养创新能力。

3、简洁性思维导图摒弃了繁琐的文字描述，用简洁的关键词和图形来表达关键信息。

这有助于减轻学生的认知负担，提高信息处理的效率。

4、个性化每个人绘制的思维导图都可以根据自己的理解和思维方式进行创作，具有很强的个性化特点。

这种个性化的表达方式能够激发学生的学习兴趣和主动性。

二、思维导图在高中数学复习教学中的应用优势1、帮助学生构建知识体系高中数学知识点繁多，且相互之间存在着紧密的联系。

在复习过程中，学生往往容易陷入细节，忽略知识的整体框架。

思维导图可以引导学生从宏观上把握知识体系，将零散的知识点整合起来，形成一个有机的整体。

例如，在复习函数这一章节时，学生可以以“函数”为中心主题，分支为函数的概念、性质、图像、常见函数类型等，再进一步细分每个分支的具体内容。

这样，学生就能清晰地看到函数知识的全貌，理解各个知识点之间的逻辑关系。

逻辑推理用思维导图学数学It was last revised on January 2, 2021逻辑推理例1．一个正方体的6个面上分别标有1，2，3，4，5，6这6个数字，从3个不同角度看正方体如下图所示，问这个正方体每个数字的对面各是什么数字？练习1.下图是面上标有1、2、3、4、5、6的正方体的三种不同的摆法，问这个正方体每个数字的对面各是什么数字？例2. 甲、乙、丙分别在南京、西安、苏州工作，他们的职业分别是工人、农民和教师。

己知:①甲不在南京工作，②乙不在苏州工作，③在苏州工作的是工人④在南京工作的不是教师⑤乙不是农民。

三人各在什么地方工作各是什么职业练习2. 甲、乙、丙三人分别是跳伞、游泳和田径运动员。

又知:①乙从未上过天②跳伞运动员己得过两块金牌③丙还没得过第一名，他比田径运动员的年龄小一点。

请判断甲、乙、丙各是什么运动员?练习3.张、王、李三个人在甲、乙、丙三个工厂里，分别当车工、钳工、电工。

已知：A 、张不在甲厂; B、王不在乙厂; C、在甲厂的不是钳工; D 、在乙厂的是车工;E 、王不是电工。

这三个人分别在哪个工厂干什么工种练习4. 甲、乙、丙三人在一起谈话。

他们当中一位是校长，一位是教师，一位是学生家长。

现在只知道:①丙比家长年龄大，②甲和教师不同岁，③老师比乙年龄小。

你能确定谁是校长，谁是老师，谁是家长吗？例3. 李老师、王老师、张老师在语文、数学、思想品德、科学、音乐和图画六门课中，每人分别都教两门。

已知：（1）思想品德老师与数学老师是好朋友;（2）王老师最年轻;（3）科学老师比语文老师年纪大;（4）李老师常向科学老师和数学老师说起他的学生;（5）王老师、音乐老师和语文老师常在一起下棋。

请分析一下，三位都是各教哪两门功课？练习5. 一次羽毛球邀请赛中，来自湖北、广东、福建、北京和上海的五名运动员相遇在一起。

据了解:①李兵和两名运动员比赛过。

②上海运动员和三名运动员比赛过。

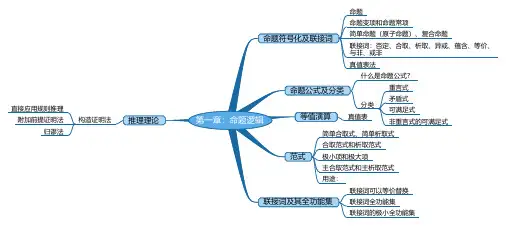
重言式
矛盾式可满足式非重言式的可满足式直接应用规则推理附加前提证明法
归谬法命题
命题变项和命题常项
简单命题（原子命题）、复合命题
联接词：否定、合取、析取、异或、蕴含、等价、与非、或非
什么是命题公式？
分类
真值表简单合取式、简单析取式
合取范式和析取范式
极小项和极大项
用途：
联接词可以等价替换
联接词全功能集
联接词的极小全功能集构造证明法真值表法
主合取范式和主析取范式
命题符号化及联接词命题公式及分类等值演算范式联接词及其全功能集推理理论第一章：命题逻辑。

初中数学八年级上册思维导图一、数的开方1. 平方根：如果一个正数x的平方等于a，那么x是a的平方根，记作x=√a。

正数a的平方根有两个，它们互为相反数，分别记作√a和√a。

0的平方根是0。

2. 立方根：如果一个数x的立方等于a，那么x是a的立方根，记作x=³√a。

立方根只有一个。

3. 算术平方根：正数a的正的平方根，记作√a，称为a的算术平方根。

4. 立方根的性质：①正数的立方根是正数；②负数的立方根是负数；③0的立方根是0。

二、实数1. 实数的概念：实数包括有理数和无理数。

有理数是可以表示为两个整数比的数，无理数是不能表示为两个整数比的数。

2. 实数的分类：①正实数；②负实数；③零。

3. 实数的运算：实数的加减乘除运算与有理数的运算类似，但需要注意无理数的运算。

三、二次根式1. 二次根式的概念：形如√a的式子，其中a≥0，称为二次根式。

2. 二次根式的性质：①√a²=a（a≥0）；②（√a）²=a（a≥0）；③√ab=√a√b（a≥0，b≥0）；④√a²+b²=√a²+√b²（a≥0，b≥0）。

3. 二次根式的运算：二次根式的加减乘除运算与有理数的运算类似，但需要注意无理数的运算。

四、一元二次方程1. 一元二次方程的概念：形如ax²+bx+c=0（a≠0）的方程，称为一元二次方程。

2. 一元二次方程的解法：①配方法；②求根公式法；③因式分解法。

3. 一元二次方程的根的判别式：判别式△=b²4ac，当△>0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△<0时，方程没有实数根。

五、不等式1. 不等式的概念：表示不相等关系的式子称为不等式。

2. 不等式的性质：①两边同时加上或减去同一个数，不等号方向不变；②两边同时乘以或除以同一个正数，不等号方向不变；③两边同时乘以或除以同一个负数，不等号方向改变。

初中数学七年级上册思维导图一、数与代数1. 实数有理数整数正整数、负整数、0分数正分数、负分数无理数不能表示为两个整数比的数无理数的近似值2. 代数式代数式的概念代数式的化简代数式的求值3. 方程与不等式一元一次方程方程的解法方程的应用一元一次不等式不等式的解法不等式的应用二、几何1. 平面几何点、线、面角锐角、直角、钝角角的度量多边形三角形等腰三角形、等边三角形、直角三角形四边形矩形、正方形、平行四边形、梯形圆圆的性质圆的周长、面积2. 空间几何立体图形长方体、正方体、圆柱、圆锥、球立体图形的表面积、体积三、统计与概率1. 统计数据的收集与整理数据的表示表格、条形图、折线图、扇形图数据的分析平均数、中位数、众数2. 概率概率的概念概率的计算概率的应用四、数学思维方法1. 分类讨论法2. 类比法3. 归纳法4. 反证法五、数学应用与建模1. 数学在实际生活中的应用金融领域利息计算、复利计算工程领域测量、绘图、计算科学研究数据分析、实验设计2. 数学建模建模的基本步骤提出问题、建立模型、求解模型、验证模型常见的数学模型线性模型、非线性模型、概率模型六、数学思维导图的制作与应用1. 思维导图的制作方法确定中心主题画出分支填充内容修饰美化2. 思维导图的应用场景学习规划项目管理决策分析七、数学与科技的发展1. 数学在科技领域的重要性计算机科学算法设计、数据结构机器学习、深度学习物理学量子力学、相对论2. 数学与其他学科的交叉融合数学与生物学遗传算法、神经网络数学与经济学博弈论、优化理论八、数学教育的创新与改革1. 数学教育的现状与问题教学方法单一学生兴趣不高创新能力培养不足2. 数学教育的创新策略案例教学法项目式学习翻转课堂在线教育3. 数学教育的改革方向注重学生个性化发展培养学生的数学思维提高学生的数学应用能力初中数学七年级上册思维导图一、数的认识1. 整数自然数：0, 1, 2, 3,正整数：1, 2, 3,负整数：1, 2, 3,整数：自然数和负整数的统称2. 分数真分数：分子小于分母的分数假分数：分子大于或等于分母的分数分数的基本性质：分子分母同时乘以或除以同一个非零整数，分数的值不变3. 小数小数的表示方法：整数部分和小数部分小数的性质：小数点向右移动一位，相当于乘以10；小数点向左移动一位，相当于除以10二、数的运算1. 整数的运算加法：将两个整数相加减法：将一个整数从另一个整数中减去乘法：将两个整数相乘除法：将一个整数除以另一个非零整数2. 分数的运算加法：将两个分数的分子相加，分母保持不变减法：将一个分数的分子从另一个分数的分子中减去，分母保持不变乘法：将两个分数的分子相乘，分母相乘除法：将一个分数的分子乘以另一个分数的分母，分母乘以另一个分数的分子3. 小数的运算加法：将两个小数的小数部分相加，整数部分相加减法：将一个小数的小数部分从另一个小数的小数部分中减去，整数部分相减乘法：将两个小数相乘除法：将一个小数除以另一个非零小数三、方程与不等式1. 方程一元一次方程：ax + b = 0（a, b为常数，x为未知数）方程的解：使方程成立的未知数的值2. 不等式一元一次不等式：ax + b > 0 或 ax + b < 0（a, b为常数，x 为未知数）不等式的解集：满足不等式的未知数的值的集合四、函数与图形1. 函数定义：函数是一种特殊的关系，每个输入值对应唯一的输出值表示方法：函数关系可以用函数表达式、函数图像、函数表格等方式表示2. 图形直线：一次函数的图像抛物线：二次函数的图像双曲线：反比例函数的图像五、统计与概率1. 统计数据的收集与整理：收集数据、整理数据、制作统计图表数据的分析与解释：分析数据、得出结论、解释结论2. 概率概率的定义：某个事件发生的可能性概率的计算：根据事件发生的次数和总次数计算概率初中数学七年级上册思维导图六、几何图形的认识1. 点、线、面点：没有长度、宽度和高度的几何元素线：只有长度没有宽度和高度的几何元素面：具有长度和宽度的几何元素2. 平面图形三角形：由三条线段组成的闭合图形四边形：由四条线段组成的闭合图形圆：由一个点到平面上所有点的距离相等的点的集合3. 空间图形立方体：由六个正方形面组成的立体图形圆柱：由两个平行圆面和一个侧面组成的立体图形圆锥：由一个圆面和一个侧面组成的立体图形七、几何图形的性质1. 三角形的性质内角和定理：三角形的内角和等于180度等腰三角形的性质：底角相等，底边上的高、中线、角平分线互相重合直角三角形的性质：直角边上的高、中线、角平分线互相重合2. 四边形的性质平行四边形的性质：对边平行且相等，对角相等，对角线互相平分矩形的性质：四个角都是直角，对边平行且相等，对角线互相平分且相等菱形的性质：四个角都是直角，对边平行且相等，对角线互相垂直平分3. 圆的性质圆的周长公式：C = 2πr（r为圆的半径）圆的面积公式：A = πr²圆的性质：圆心到圆上任意一点的距离都相等八、几何图形的计算1. 三角形的计算三角形的周长：三条边的长度之和三角形的面积：底乘以高除以22. 四边形的计算四边形的周长：四条边的长度之和四边形的面积：根据不同类型的四边形使用相应的公式计算3. 圆的计算圆的周长：2πr圆的面积：πr²九、综合应用1. 实际问题运用所学的数学知识解决实际问题，如计算面积、周长、体积等培养学生的应用意识和解决问题的能力2. 数学建模将实际问题抽象成数学模型，运用数学知识解决问题培养学生的建模能力和创新能力3. 数学探究通过探究活动，让学生发现数学规律，提高学生的探究能力和思维能力初中数学七年级上册思维导图十、数学思维与方法1. 逻辑推理通过观察、分析、归纳等方法，培养学生的逻辑思维能力帮助学生理解数学概念、性质、定理之间的关系2. 数学建模将实际问题抽象成数学模型，运用数学知识解决问题培养学生的建模能力和创新能力3. 数学探究通过探究活动，让学生发现数学规律，提高学生的探究能力和思维能力十一、数学素养与能力1. 数感培养学生对数的敏感性，能够快速、准确地理解和处理数学信息2. 空间观念培养学生对几何图形的认识和空间想象能力，提高学生的空间思维能力3. 解决问题的能力培养学生运用数学知识解决实际问题的能力，提高学生的应用意识和实践能力4. 创新能力培养学生的创新思维，鼓励学生尝试不同的解题方法和思路5. 合作与交流能力培养学生与他人合作交流的能力，提高学生的团队协作能力和沟通能力初中数学七年级上册思维导图一、数与代数1. 实数有理数整数正整数、负整数、0分数正分数、负分数无理数不能表示为两个整数比的数无理数的近似值2. 代数式代数式的概念代数式的化简代数式的求值3. 方程与不等式一元一次方程方程的解法方程的应用一元一次不等式不等式的解法不等式的应用二、几何1. 平面几何点、线、面角锐角、直角、钝角角的度量多边形三角形等腰三角形、等边三角形、直角三角形四边形矩形、正方形、平行四边形、梯形多边形的内角和定理2. 空间几何立体图形正方体、长方体、圆柱、圆锥、球立体图形的表面积与体积三、统计与概率1. 数据的收集与整理数据的收集方法数据的整理方法2. 数据的描述平均数、中位数、众数极差、方差、标准差3. 概率概率的基本概念概率的计算方法概率的应用四、数学思维方法1. 归纳法从具体到一般从特殊到一般2. 类比法通过相似性进行推理3. 反证法假设结论不成立，推出矛盾，从而证明结论成立4. 构造法通过构造实例来解决问题五、数学建模1. 建模的基本步骤确定问题建立模型求解模型验证模型2. 常见的数学模型线性模型二次模型指数模型3. 数学建模的应用在实际生活中的应用在科学研究中的应用初中数学七年级上册思维导图六、数学实验与探究1. 实验的设计与实施确定实验目的设计实验方案实施实验并记录数据分析实验结果2. 探究的方法与技巧观察法实验法归纳法类比法3. 数学实验与探究的应用解决实际问题深化数学理解培养创新思维七、数学文化1. 数学发展史古代数学近现代数学2. 数学家的故事中国数学家外国数学家3. 数学与生活的关系数学在科技发展中的作用数学在日常生活中的应用八、数学学习方法1. 课堂学习专心听讲积极思考勇于提问2. 自主学习制定学习计划完成课后作业复习巩固3. 合作学习与同学交流讨论分享学习资源相互帮助、共同进步九、数学素养的培养1. 数学思维逻辑思维抽象思维空间思维2. 数学能力计算能力推理能力解决问题的能力3. 数学品质耐心细心持之以恒初中数学七年级上册思维导图十、数学竞赛与拓展1. 数学竞赛简介数学竞赛的类型数学竞赛的级别数学竞赛的报名时间及方式2. 数学竞赛的备考策略基础知识的巩固解题技巧的提升模拟试题的训练3. 数学竞赛的意义激发学习兴趣培养竞争意识提高数学能力十一、数学与科技1. 数学在科技领域的作用计算机科学数据分析2. 数学在工程技术中的应用建筑设计机械制造通信技术3. 数学在生活中的创新数学与艺术数学与体育数学与游戏十二、数学教育改革与发展1. 新课程标准的实施课程目标的调整教学内容的更新教学方法的改革2. 数学教育技术的发展信息技术与数学教育的融合在线教育平台的建设虚拟现实技术在数学教学中的应用3. 数学教育的国际交流与合作国际数学竞赛的参与数学教育研究的合作数学教师培训的国际交流。

人教版五年级上册数学全册思维导图一、数与代数1. 整数的认识自然数、整数、正数、负数、绝对值、相反数、倒数2. 分数的认识分数、真分数、假分数、带分数、分数的基本性质、约分、通分3. 小数的认识小数、小数点、小数的基本性质、小数的加减乘除、小数的四则混合运算4. 比较大小整数、分数、小数的大小比较5. 数的估算整数、分数、小数的估算方法二、空间与图形1. 图形的认识点、线、面、体、平面图形、立体图形2. 图形的周长和面积线段、角的周长，正方形、长方形、平行四边形、梯形的面积，圆的周长和面积3. 图形的变换平移、旋转、对称、相似、放大与缩小4. 三角形三角形的定义、性质、分类、内角和、外角和、三角形的稳定性5. 四边形四边形的定义、性质、分类、平行四边形、矩形、菱形、正方形的性质和判定三、统计与概率1. 数据的收集与整理调查问卷、统计表、统计图（条形图、折线图、扇形图）2. 数据的分析与处理平均数、中位数、众数、方差、标准差3. 概率事件、必然事件、不可能事件、随机事件、概率的计算方法四、解决问题1. 问题解决的基本步骤提出问题、分析问题、制定计划、解决问题、回顾与反思2. 解决问题的策略图形法、列表法、树状图法、表格法、枚举法、方程法、逻辑推理法3. 解决问题的应用实际问题、数学问题、逻辑问题、趣味问题人教版五年级上册数学全册思维导图五、数学实践活动1. 数学实验通过实际操作，验证数学规律，如利用图形拼摆验证勾股定理、利用实验数据验证概率等2. 数学游戏设计与数学相关的游戏，如24点游戏、数独、数学谜题等，培养数学兴趣和思维3. 数学故事通过讲述数学故事，激发学生对数学的兴趣，如数学家的故事、数学趣闻等4. 数学竞赛组织数学竞赛，提高学生的数学素养和竞争意识，如口算比赛、解题比赛等六、数学文化1. 数学史了解数学发展的历史，如古代数学、现代数学、数学家的贡献等2. 数学名人认识数学领域的杰出人物，如欧几里得、阿基米德、高斯等3. 数学趣闻学习数学趣闻，如数学笑话、数学谜语、数学趣题等，增加学生对数学的了解和兴趣4. 数学与生活探讨数学在生活中的应用，如购物、旅游、理财等，让学生体会到数学的实用性七、数学与科技1. 数学与计算机了解计算机科学中的数学原理，如算法、数据结构、编程语言等2. 数学与物理探讨数学在物理学中的应用，如牛顿力学、电磁学、量子力学等3. 数学与生物了解数学在生物学中的应用，如遗传学、生态学、生物信息学等4. 数学与经济探讨数学在经济领域中的应用，如统计学、运筹学、博弈论等八、数学与艺术1. 数学与音乐了解音乐中的数学原理，如音阶、节奏、和声等2. 数学与绘画探讨绘画中的数学元素，如黄金分割、透视法、几何图形等3. 数学与建筑了解建筑中的数学原理，如比例、对称、结构稳定性等4. 数学与雕塑探讨雕塑中的数学元素，如几何形状、比例、空间关系等人教版五年级上册数学全册思维导图九、数学学习策略1. 预习与复习通过预习了解新知识，复习巩固已学知识，形成完整的知识体系2. 课堂笔记记录关键知识点、解题思路、易错点等，便于课后复习和查阅3. 作业与练习认真完成作业，及时巩固所学知识，通过练习提高解题能力4. 课外阅读阅读数学课外书籍、杂志、网络资源等，拓宽数学视野，增加知识储备5. 小组讨论与合作学习与同学一起讨论问题，分享学习心得，互相学习、互相帮助十、数学与思维1. 逻辑思维通过数学学习，培养逻辑思维能力，如归纳、演绎、推理等2. 空间想象通过几何图形的学习，培养空间想象力，如三维图形的构造、空间位置关系等3. 创新思维鼓励学生从不同角度思考问题，提出新颖的解题方法，培养创新意识4. 解决问题的能力通过数学问题的解决，提高学生分析问题、解决问题的能力5. 数学建模学习将实际问题转化为数学模型，培养学生的建模能力人教版五年级上册数学全册思维导图一、认识数学数学是研究数量、结构、变化以及空间等概念的学科。

教材分析：本单元是非常有趣的数学活动，也是逻辑思维训练的起始课。

逻辑推理能力是人们在生活、学习工作中很重要的能力。

本单元主要要求学生能根据提供的信息，借助集合圈进行判断、推理，得出结论，使学生初步接触和运用集合圈分析问题、解决问题。

教材试图通过一些生动有趣的简单事例，运用操作、实验、猜测等直观手段解决这些问题，渗透数学的思想方法，初步培养学生借助几何直观思考问题的意识。

教学目标：1、在具体情境中使学生感受集合的思想，感知集合图的产生过程。

2、能借助直观图，利用集合的思想方法解决简单的实际问题，同时使学生在解决问题的过程中进一步体会集合的思想，进而形成策略。

3、渗透多种方法解决重叠问题的意识，培养学生善于观察、勤于思考的学习习惯。

教学重点：让学生感知集合的思想，并能初步用集合的思想解决简单的实际问题。

教学难点：对重叠部分的理解。

课前准备：课件、呼啦圈2个、磁性圆片教学过程：一、创设探究情境，引领学生初步感知。

1、创设情境，激发兴趣。

脑筋急转弯：两位爸爸和两位儿子一同去海洋世界（每人都得买一张票），可是他们只买了3张票，便顺利地进去了。

这是为什么？学生活动：学生猜测各种可能性，你一言我一语地发表自己的高见。

2、设置悬念，引人入胜师：“大家的猜测都有自己的道理，但答案到底是什么呢？暂时老师还不想告诉你们，我想通过下面的活动，大家一定能自己找到答案的。

”二、创设实践情境，引领学生深入理解。

（一）报名参加数学比赛：四宫数独和六宫数独1、师：三年级一班有3名学生报名参加了四宫数独，4名学生报名参加了六宫数独。

2、出示参加四宫、六宫数独比赛的学生名单：四宫：子宜、佳琳、俊轩六宫：子宜、晓晴、子凌、方华3、数一数，参加四宫的有几位同学？（3人）参加六宫的有几位同学？（4人）师：一共有几人参加比赛？生：7人或6人。

师：究竟是6人？还是7人呢？我们请这些同学上台，让我们一起数一数，好吗？请以上名字的同学上台（同学们一起喊他们的名字）四宫站在左边，六宫站在右边。