几何的五大模型 ppt课件

、等面积变换模型⑴等底等高的两个三角形面积相等；反之，如果S A ACD BCD，则可知直线AB平行于CD等底等高长方形-平行四边形-梯形的面积相等；三角形面积等于与它等底等高的平行四边形面积的一半；正方形的面积等于对角线长度平方的一半；⑵两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比。

如上图S =a :b、共角定理（鸟头定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角（相等角或互补角）两夹边的乘积之比。

如图，在△ ABC中，D,E分别是AB,AC上的点（如图1）或D在BA的延长线上，E在AC上（如图2)，则SA ABC :SA ADE 二(AB AC)：(AD AE)三、蝴蝶定理模型（不规则四边形的面积问题）①或者s S3P S4 ② AO:OC =I S S2 ： S4 S3梯形中：①S I：S B二a2：b2图2②S!: S3 : S2: S4 =a2 :b2: ab: ab ；不论大小怎样改变它③梯形S 的对应份数为a b 2四、相似模型B G金字塔模型① AD _ AE _ DE _ AF AB AC BC AG所谓的相似三角形， 就是形状相同，大小不同的三角形（只要其形状不改变, 们都相似），与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方。

五、燕尾定理模型B E CS A ABG : S A AGC =S A BGE : S A EGC = BE ：ECS A BGA : S A BGC =S A AGF ： S^FGC =AF : FCS A AGC : S ABCG =S A ADG ：&DGB =AD : DB ② S ^ADE :S ^ABC 二 AF 2: AG 2。

沙漏模型0.15倍，黄色三角形的面积是 如图，三角形田地中有两条小路 AE 和CF ,交叉处为D ,张大伯常走这两条小路, 且AD = 2DE 。

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等(2)两个三角形高相等，面积比等于它们的底之比(3)两个三角形底相等，面积比等于它们的高之比如左图S1: S2=a:b(4)夹在一组平行线之间的等积变形，如右上图，SAABC= S △ BAD反之，如果S △ BCD则可知直线AB平行于CD (AB// CDSAABC=二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图在△ ABC中，D, E分别是AB AC上的点如图•(或D在BA的延长线上，E 在AC 上)，贝s S ABO :S AADE=(AB X AC)：(AD X AE)T D图CoJI/u//\//（B・....................推理过程连接BE再利用等积变换模型即可。

证明：图(1)中设：过顶点D做底边AE的高为H1 ；过顶点B做底边AC的高为H2△ ABE 中SA ADE SA ABE=AD AB同理SAADE SAABE=HI H2 AD : AB= HI： H2 }又因SAADE=AE*H1*1^ AA S AABC=AC*H2*V2 得出SAADE SAABC=AE*H1 AC*H2所以SAADE SA ABC=(Ax AC):(AD x AE)图(2)中设过顶点D作底边AE的高为H1，过顶点B做底边AC的高为H2ADBE 中，SA ADE SA ABE=AD ABS A ADE SA ABE= H1: H2 AD : AB= H1: H2又因SAADE=AE*H1*V2S AABC=AC*H2*V2 得岀SAADE SAABC=AE*H1 AC*H2所以SA ADE SA ABC=(Ax AC):(ADx AE)三、蝴蝶定理模型任意四边形中的比例矢系(“蝴蝶定理”)①S1 :S2=S4:S3 或者S1 X S3=S2x S4②AO:OC=(S1+S2)：(S4+S3)证明(1):在乂 ABD 中，S1： S2=DO:OB在厶DCB 中，S4: S3=DO OB 得至(J S1 :S2=S4:S3 或者S1 x S3=S2X S4(十字相乘法)证明(2): 设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)= ( AO*H1*1^+AO*H2*V2) : ( OC*H1*1^+ OC*H2*V2)约分得到:(S1+S2):(S4+S3)=AO : OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。

数 学 几 何 五 大 模 型一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比。

如上图12::S S a b =⑶夹在一组平行线之间的等积变形，如下图ACD BCD S S =△△；反之，如果ACDBCD S S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；⑸三角形面积等于与它等底等高的平行四边形面积的一半； 二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S 1S 2S ab图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：（1） 1243::S S S S =或者1324S S S S ⨯=⨯（2）()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)（1）2213::S S a b =（2）221324::::::S S S S a b ab ab =；（3）梯形S 的对应份数为()2a b +。

四、相似模型相似三角形性质：金字塔模型 沙漏模型（1）AD AE DE AFAB AC BC AG===； （2）22::ADE ABCS S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方。

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等⑵两个三角形高相等，面积比等于它们的底之比⑶两个三角形底相等，面积比等于它们的高之比如左图S1: S2=a:b(4)夹在一组平行线之间的等积变形，如右上图，S AABC= S △BAD反之，如果S\ABC= S ABCD,则可知直线AB平行于CD (AB// CD二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图在△ ABC中, D, E分别是AB, AC上的点如图.(或D在BA的延长线上, E在AC上)，贝卩S AABC： S AD E=(AB X AC):(AD X AE)推理过程连接BE再利用等积变换模型即可。

证明：图(1)中设：过顶点D做底边AE的高为H1;过顶点B做底边AC的高为H2△ ABE中SA ADE SA ABE=A：AB同理SA ADE SA ABE=H1 H2 AD : AB= H1: H2 L又因SAADE=AE*H1*1/2S △ ABC=AC*H2*1/2 得出SA ADE SA ABC=AE*H1 AC*H2所以SA ADE SA ABC=(AX AC):(AD X AE)图(2)中设过顶点D作底边AE的高为H1,过顶点B做底边AC的高为H2△ DBE中，SA ADE SA ABE二AD ABS A ADE SA ABE= H1 H2 AD : AB= HI: H2又因SAADE=AE*H1*1/2S A ABC=AC*H2*1/2 得出SA ADE SA ABC=AE*H1 AC*H2所以SA ADE SA ABC=(AB< AC):(AD X AE)三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3 或者S1 X S3=S2X S4②AO:OC=(S1+S2):(S4+S3)证明(1):在A ABD中, S1 : S2=DO:OB在A DCB中, S4: S3二DO OB 得至U S1:S2=S4:S3 或者S1 X S3=S2X S4(十字相乘法)证明(2):设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)= (AO*H1*1/2+AO*H2*1/2): ( OC*H1*1/2+ OC*H2*1/2) 约分得到：(S1+S2):(S4+S3)=AO : OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。

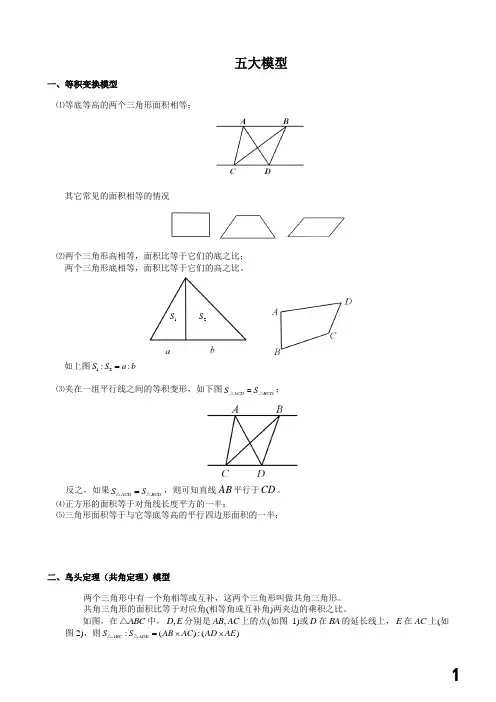
一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比。

如上图12::S S a b =⑶夹在一组平行线之间的等积变形，如下图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；⑸三角形面积等于与它等底等高的平行四边形面积的一半；二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△五大模型1S 2S图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =； ③梯形S 的对应份数为()2a b +。

四、相似模型相似三角形性质：金字塔模型 沙漏模型①AD AEDE AFAB AC BC AG===； ②22::ADE ABC S S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方。

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等(2)两个三角形高相等，面积比等于它们的底之比(3)两个三角形底相等，面积比等于它们的高之比如左图S1：S2=a:b(4)夹在一组平行线之间的等积变形，如右上图，S△ABC= S△BAD反之，如果S△ABC= S△BCD，则可知直线AB平行于CD （AB∥CD）二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图在△ABC中，D，E分别是AB，AC上的点如图.(或D在BA的延长线上，E在AC上)，则S△ABC：S△ADE=(AB×AC):(AD×AE)推理过程连接BE，再利用等积变换模型即可。

证明：图（1）中设：过顶点D做底边AE的高为H1；过顶点B做底边AC的高为H2△ABE中S△ADE：S△ABE=AD：AB同理S△ADE：S△ABE=H1：H2 AD：AB= H1：H2又因S△ADE=AE*H1*1/2S△ABC=AC*H2*1/2 得出S△ADE：S△ABC=AE*H1：AC*H2 所以S△ADE：S△ABC=(AB×AC):(AD×AE)图（2）中设过顶点D作底边AE的高为H1，过顶点B做底边AC的高为H2△DBE中，S△ADE：S△ABE=AD：ABS△ADE：S△ABE= H1：H2 AD：AB= H1：H2又因S△ADE=AE*H1*1/2S△ABC=AC*H2*1/2 得出S△ADE：S△ABC=AE*H1：AC*H2所以S△ADE：S△ABC=(AB×AC):(AD×AE)三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3 或者 S1×S3=S2×S4②AO:OC=(S1+S2):(S4+S3)证明（1）：在△ABD中，S1：S2=DO:OB在△DCB中，S4：S3=DO：OB 得到S1:S2=S4:S3或者 S1×S3=S2×S4(十字相乘法)证明（2）：设过D点作底边AC的高为H1，过B点作底边AC的高为H2(S1+S2):(S4+S3)=（AO*H1*1/2+AO*H2*1/2）：（OC*H1*1/2+ OC*H2*1/2）约分得到：(S1+S2):(S4+S3)=AO：OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。