考研数学定积分的物理应用

Born To Win人生也许就是要学会愚忠。

选我所爱，爱我所选。

考研数学之物理应用分析数学一和数学二的学生对物理应用这一块掌握的比较薄弱。

物理应用不是数学一和数学二的常考点，但是一旦考了，学生往往都不会。

2015年数学二的考研真题出了一道与物理应用有关的大题。

这是个拉分题，很多同学都不会。

所以希望大家能够对物理应用有足够的重视，特别是那些立志上名校，希望数学给力的学生。

下面，跨考教育数学教研室的向喆老师就来和大家分享物理应用分析的学习方法。

一.明确知识框架有句古语：知己知彼，百战不殆。

物理应用可以说是比较难的知识点，所以大家就应该明了考研都考了那些物理应用。

首先，只有数学一和数学二才考物理应用。

然后，物理应用分布在导数应用，定积分应用，微分方程应用中，其中物理应用在定积分中考查的最多。

最后，有关的物理知识的储备。

比如说速率，做功，压强，压力等。

二.掌握学习方法大家在明白了物理应用的体系后，就应该掌握相应的学习方法。

首先是导数中的物理应用。

通过对历年真题的研究，我发现导数的物理应用主要体现在对导数物理意义的理解，即速率。

然后是定积分中的物理应用。

这是考查的重点。

主要包括：变力做功(变力对质点沿直线做功和克服重力做功);液体静压力;质心及形心。

这三个部分求解的核心思想是微元法：分割，近似，求和，取极限。

大家应该把定积分的定义即曲边梯形面积是怎么求得掌握。

接着，大家就应该把这三部分的微元法思想推一遍，从而熟练掌握本质的含义。

其中克服重力做功问题已经在真题中出现过。

最后是微分方程中的物理应用。

通过历年考题分析，我发现微分方程中的物理应用主要考察的是牛顿第二定律。

据此联系了位移与速率;重力，浮力及阻力与加速度关系。

总之，在学习这部分知识时候，应该有一些基本的思想。

比如说：微元法思想，牛顿第二定律，压强及压力，位移与速率等。

三.熟练掌握题型大家在明白了知识体系以及学习方法后就应该通过做题来巩固。

不过现在出现了一个问题：数学一和数学二的同学有很多都不是学物理的。

第1篇一、面试题目1. 请简述数学分析中极限的定义和性质。

解析：数学分析中，极限是指当自变量x趋向于某一点a时，函数f(x)的值趋向于某一点L。

具体来说，如果对于任意给定的正数ε，都存在一个正数δ，使得当0<|x-a|<δ时，有|f(x)-L|<ε，则称函数f(x)当x趋向于a时极限为L，记作lim(x→a)f(x)=L。

2. 请解释数学中的导数的概念及其几何意义。

解析：导数是描述函数在某一点处的局部变化率。

对于函数y=f(x)，在点x0处的导数表示为f'(x0)。

几何意义上，导数表示曲线在该点的切线斜率。

3. 请简述多元函数偏导数的概念及其几何意义。

解析：多元函数偏导数是指多元函数在某一点处，仅考虑一个变量变化时，函数的导数。

对于多元函数z=f(x,y)，在点(x0,y0)处的偏导数表示为f_x'(x0,y0)和f_y'(x0,y0)。

几何意义上，偏导数表示曲线在该点的切线斜率。

4. 请解释定积分的概念及其物理意义。

解析：定积分是指将一个函数在一个区间上的无穷小分割，然后求和并取极限的过程。

物理意义上，定积分可以表示曲线下方的面积、物理量在某段时间内的累积量等。

5. 请简述多元函数的积分概念及其物理意义。

解析：多元函数的积分是指将一个多元函数在一个区域上的无穷小分割，然后求和并取极限的过程。

物理意义上，多元函数的积分可以表示空间曲面的面积、物理量在某区域内的累积量等。

6. 请解释数学中的级数收敛的概念。

解析：级数收敛是指一个无穷级数的各项之和趋向于某个确定的值。

如果对于任意给定的正数ε，都存在一个正整数N，使得当n>N时，级数的部分和S_n与该确定值L之差的绝对值小于ε，则称该级数收敛。

7. 请简述线性代数中矩阵的概念及其运算。

解析：矩阵是一种由数字组成的矩形阵列，表示线性变换、线性方程组等。

矩阵的运算包括加法、数乘、乘法等。

8. 请解释线性代数中行列式的概念及其性质。

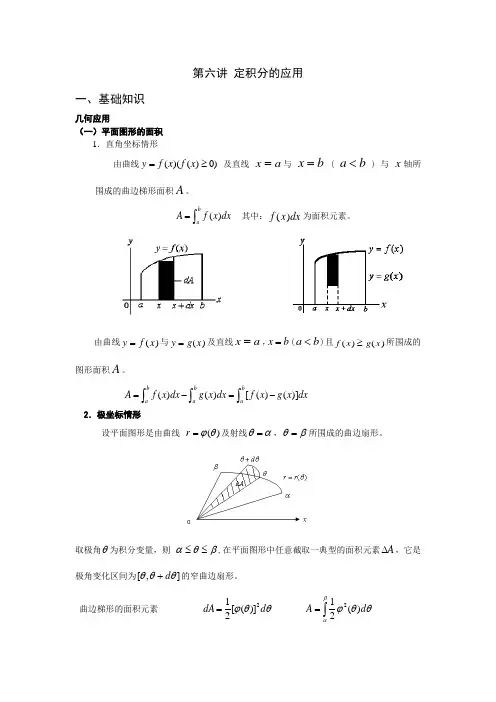
第六讲 定积分的应用一、基础知识几何应用（一）平面图形的面积 1．直角坐标情形由曲线)0)(()(≥=x f x f y 及直线 x a =与 x b = ( a b < ) 与 x 轴所围成的曲边梯形面积A 。

()baA f x dx =⎰ 其中：f x dx ()为面积元素。

由曲线y f x =()与y g x =()及直线x a =，x b =(a b <)且f x g x ()()≥所围成的图形面积A 。

()()[()()]=-=-⎰⎰⎰b b baaaA f x dx g x dx f x g x dx2．极坐标情形设平面图形是由曲线 )(θϕ=r 及射线αθ=，βθ=所围成的曲边扇形。

取极角θ为积分变量，则 βθα≤≤,在平面图形中任意截取一典型的面积元素A ∆，它是极角变化区间为],[θθθd +的窄曲边扇形。

曲边梯形的面积元素 θθϕd dA 2])([21= ⎰=βαθθϕd A )(212（二）旋转体的体积计算由曲线y f x =()直线x a =，x b =及x 轴所围成的曲边梯形，绕x 轴旋转一周而生成的立体的体积。

取x 为积分变量，则],[b a x ∈，对于区间],[b a 上的任一区间],[dx x x +，它所对应的窄曲边梯形绕x 轴旋转而生成的薄片似的立体的体积近似等于以)(x f 为底半径，dx 为高的圆柱体体积。

即：体积元素为 []dx x f dV 2)(π=所求的旋转体的体积为 []dx x f V ba⎰=2)(π（三）平面曲线的弧长 1.直角坐标情形设函数)(x f 在区间],[b a 上具有一阶连续的导数，计算曲线)(x f y =的长度s 。

取x 为积分变量，则],[b a x ∈,在],[b a 上任取一小区间],[dx x x +，弧长元素为[]dx x f ds 2)(1'+= 弧长为 []⎰'+=badx x f s 2)(12.参数方程的情形若曲线由参数方程)()()(βαφϕ≤≤⎩⎨⎧==t t y t x 给出，弧微分[][]dt t t dy dx ds 2222)()()()(φϕ'+'=+=则 [][]⎰'+'=βαφϕdt t t s 22)()(3.极坐标情形若曲线由极坐标方程)()(βθαθ≤≤=r r 给出，将极坐标方程化成参数方程，曲线的参数方程为x r y r ==⎧⎨⎩≤≤()cos ()sin ()θθθθαθβ，弧长元素为θθθθθθθd r r d r r d r r dy dx ds 22222222)()cos sin ()()sin cos ()()('+=+'+-'=+= 从而有 ⎰'+=βαθd r r s 22（四）.曲率与曲率半径 曲率记作,k 0lims d k s dsαα∆→∆==∆, 222''''tan '''sec sec 1'd d y y y y dx dx y ααααα=⇒=⋅⇒==+, 2''1'y d dx y α=+,又,ds =故322''(1')y d k dsy α==+.曲率半径 3221(1')''y k y ρ+==. 曲率圆二、例题1．平面图形的面积与旋转体的体积例 1. 已知抛物线2,y px qx =+(其中0,0p q <>)在第一象限内与直线5x y +=相切,且抛物线与x 轴所围成的平面图形的面积为s .问: (1)p q 和为何值时,s 达到最大值? (2)求出此最大值.【答案】,3p q =4=-5,22532s =例2.设⎪⎩⎪⎨⎧>≤=-0,0,)(22x ex e x F x x ，S 表示夹在x 轴与曲线()y F x =之间的面积. 对任何)(x f0t >，)(1t S 表示矩形t x t -≤≤，0()y F t ≤≤的面积. 求(I) 1()()S t S S t =-的表达式； (II) ()S t 的最小值.【答案】(I) t te t S 221)(--=，t ∈ (0 , +∞).(II) eS 11)21(-=. 例3.设曲线的极坐标方程为(0)a e a θρ=>,则该曲线上相应于θ从0到2π的一段弧与极轴所围成的图形的面积为41(1)4a e aπ-. 例 4.设1D 是由抛物线22y x =和直线x a =, 2x =及0y =所围成的平面区域; 2D 是由抛物线22y x =和直线x a =,0y =所围成的平面区域,其中02a <<.(1)试求1D 绕x 轴旋转而成的旋转体体积1V ;2D 绕y 轴旋转而成的旋转体体积2V . (2)问当a 为何值时,12V V +取得最大值?试求此最大值. 【答案】54(32)5a π- 4a π 1295π 例5.设曲线2(0,0)y ax a x =>≥与21y x =-交于点A ,过坐标原点O 和点A 的直线与曲线2y ax =围成一平面图形.问a 为何值时,该图形绕x 轴旋转一周所得的旋转体体积最大?最大体积是多少?【答案】4a =是体积最大,其最大体积为:522161518755V π=⋅= 例6.过坐标原点作曲线ln y x =的切线,该切线与曲线ln y x =及x 轴围成平面图形D . (1).求D 的面积A ;(2).求D 绕直线x e =旋转一周所得旋转体的体积V . 【答案】(1)112A e =- (2)2(5123)6V e e π=-+ 例7.（15-2） 设A>0，D 是由曲线段sin (0)2y A x x π=≤≤及直线0y =，2x π=所围成的平面区域，1V ，2V 分别表示D 绕x 轴与绕y 轴旋转成旋转体的体积，若12V V =，求A 的值.【答案】8π例8.(09-3-10 分)设曲线()y f x =，其中()y f x =是可导函数，且()0f x >，已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形，绕x 轴旋转一周所得的立体体积值是曲边梯形面积值的t π倍，求该曲线方程。

考研数学定积分物理应用公式？
答：考研数学定积分物理应用公式包括：
1. 变力做功：∫(从a到b) F(x) dx，其中F(x)是变力，a和b分别是初位置和末位置。

2. 质心公式：∫(从a到b) xρ(x) dx / ∫(从a到
b) ρ(x) dx，其中ρ(x)是线密度，用于求细棒的质量中心。

3. 引力公式：∫(从a到b) km1m2/r^2 dr，用于求两质点间的引力，其中k是引力常数，m1和m2是两质点的质量，r是两质点间的距离。

4. 压力公式：P = pA，其中p是压强，A是面积。

5. 液体静压力：∫(从h1到h2) ρgh dA，其中ρ是液体密度，g是重力加速度，h是液体深度，dA是水平面积微元。

6. 旋转体体积：∫(从a到b) π[f(x)]^2 dx，其中f(x)是旋转曲线的函数表达式。

7. 液体对侧壁的压力：∫(从a到b) 2πxlρg dx，其中l是液体高度，ρ是液体密度，g是重力加速度。

8. 物体在液体中所受的浮力：∫(从a到b) ρVg dx，其中ρ是液体密度，V是物体体积，g是重力加速度。

9. 物体绕定轴旋转的转动惯量：∫(从a到b) r^2 dm，其中r是物体上各点到转轴的距离，dm是物体上的质量微元。

10. 细棒对过端点且与棒垂直的轴的转动惯量：∫(从0到l) (1/3)ml^2 dx = (1/3)ml^2。

以上是考研数学定积分物理应用的一些常见公式。

希望这些信息对您有帮助，如果您还有其他问题，欢迎告诉我。

第1篇一、数学分析1. 请解释实数的完备性及其意义。

2. 证明：若数列{an}单调有界，则{an}收敛。

3. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

4. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

5. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

6. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

7. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

8. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

9. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

10. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

二、高等代数1. 请解释行列式的定义及其性质。

2. 证明：若矩阵A可逆，则|A|≠0。

3. 设矩阵A为n阶方阵，求证：A的行列式|A|等于其特征值的乘积。

4. 证明：若矩阵A为n阶方阵，且|A|=0，则A不可逆。

5. 设矩阵A为n阶方阵，求证：A的行列式|A|等于其特征值的乘积。

高等数学不用看的部分：第5页映射；第17页到第20页双曲正弦双曲余弦双曲正切及相应的反函数可以不记；第107页由参数方程所确定的函数的导数；第119页微分在近似方程中的应用记住几个公式4，5,6还有120页的近似公式即可，不用看例题；第140页泰勒公式的证明可以不看，例题中的几个公式一定要记住，比如正弦公式等；第169页第七节；第178页第八节；第213页第四节；第218页第五节；第280页平行截面面积为已知的立体体积；第282页平面曲线的弧长；第287页第三节；第316页第五节；在第七章微分方程中建议大家只要会解方程即可，凡是书上涉及到物理之类的例题不看跳过例如第301页的例2例3例4；第八章；第90页第六节；第101页第七节；第157页第三节；165页第四节；第十一章；第261页定理6；第278页第四节；第285页第五节；第302页第七节；第316第八节线性代数不用看的部分：第102页第五节概率论与数理统计要考的部分：第一二三四五章；第六章第135页抽样分布；第7章第一节点估计和第二节最大似然估计注意：数学课本和习题中标注星号的为不考内容，在上面的内容中我并没有标出。

上述内容是根据文都发放的教材编的。

《高等数学》目录与2010数三大纲对照的重点计划用时（天）标记及内容要求：★─大纲中要求“掌握”和“会”的内容以及对学习高数特别重要的内容，应当重点加强，对其概念、性质、结论及使用方法熟知，对重要定理、公式会推导。

要大量做题。

☆─大纲中要求“理解”和“了解”的内容以及对学习高数比较重要的内容，要看懂定理、公式的推导，知道其概念、性质和方法，能使用其结论做题●─大纲中没有明确要求，但对做题和以后的学习有帮助。

要能看懂，了解其思路和结论。

▲─超出大纲要求。

第一章函数与极限第一节映射与函数（☆集合、影射，★其余）第二节数列的极限（☆）第三节函数的极限（☆）第四节无穷小与无穷大（★）第五节极限运算法则（★）第六节极限存在准则（★）第七节无穷小的比较（★）第八节函数的连续性与间断点（★）第九节连续函数的运算与初等函数的连续性（★）第十节闭区间上连续函数的性质（★）总习题第二章导数与微分第一节导数概念（★）第二节函数的求导法则（★）第三节高阶导数（★）第四节隐函数及由参数方程所确定的函数的导数相关变化率（★）第五节函数的微分（★）总习题二第三章微分中值定理与导数的应用第一节微分中值定理（★罗尔，★拉格朗日，☆柯西）第二节洛必达法则（★）第三节泰勒公式（☆）第四节函数的单调性与曲线的凹凸性（★）第五节函数的极值与最大值最小值（★）第六节函数图形的描绘（★）第七节曲率(●)第八节方程的近似解(●)总习题三（★注意渐近线）第四章不定积分第一节不定积分的概念与性质（★）第二节换元积分法（★）第三节分部积分法（★）第四节有理函数的积分（★）第五节积分表的使用（★）总习题四第五章定积分第一节定积分的概念与性质（☆）第二节微积分基本公式（★）第三节定积分的换元法和分部积分法（★）第四节反常积分（☆概念，★计算）第五节反常积分的审敛法г函数(●)总习题五第六章定积分的应用第一节定积分的元素法（★）第二节定积分在几何学上的应用（★平面面积，★旋转体，★简单经济应用）第三节定积分在物理学上的应用（★求函数平均值）总习题六、第七章微分方程第一节微分方程的基本概念（☆）第二节可分离变量的微分方程（☆）（★掌握求解方法）第三节齐次方程（☆）（★掌握求解方法）第四节一阶线性微分方程（☆）（★掌握求解方法）第五节可降阶的高阶微分方程（☆）第六节高阶线性微分方程（☆）第七节常系数齐次线性微分方程（★二阶的）第八节常系数非齐次线性微分方程（★二阶的）第九节欧拉方程(●)第十节常系数线性微分方程组解法举例(●)总习题七附录I 二阶和三阶行列式简介附录II 几种常用的曲线附录、积分表第八章空间解析几何与向量代数（▲）第一节向量及其线性运算第二节数量积向量积混合积第三节曲面及其方程第四节空间曲线及其方程第五节平面及其方程第六节空间直线及其方程总习题八第九章多元函数微分法及其应用第一节多元函数的基本概念（☆）第二节偏导数（☆概念。

高等数学考研指定教材：同济大学数学系主编《高等数学》（上下册）（第六版）第一章函数与极限(7天)（考小题）学习内容复习知识点与对应习题大纲要求第一节：映射与函数(一般章节)函数的概念，常见的函数（有界函数、奇函数与偶函数、单调函数、周期函数）、复合函数、反函数、初等函数具体概念和形式.（集合、映射不用看；双曲正弦，双曲余弦，双曲正切不用看）习题1－1：4，5，6，7，8，9，13，15，16（重点）1．理解函数的概念，掌握函数的表示法，并会建立应用问题中的函数关系.2．了解函数的有界性、单调性、周期性和奇偶性．3．理解复合函数及分段函数的概念，了解反函数及隐函数的概念．4．掌握基本初等函数的性质及其图形，了解初等函数的概念.第二节：数列的极限(一般章节)数列定义，数列极限的性质(唯一性、有界性、保号性)（本节用极限定义证明极限的题目考纲不作要求，可不看，如P26例1，例2，例3，定理1,2,3的证明都不作要求，但要理解；定理4不用看）习题1－2：1第三节：函数的极限(一般章节)函数极限的基本性质（不等式性质、极限的保号性、极限的唯一性、函数极限的函数局部有界性,函数极限与数列极限的关系等）P33(例4,例5)（例7不用做，定理2,3的证明不用看，定理4不用看）习题1－3：1，2，3，45．理解极限的概念，理解函数左极限与右极限的概念，以及函数极限存在与左、右极限之间的关系．6．掌握极限的性质及四则运算法则.7．掌握极限存在的两个准则，并会利用它们求极限，掌握利用两个重要极限求极限的方法．8．理解无穷小量、无穷大量的概念，掌握无穷小量的比较方法，会用等价无穷小量求极限．第四节：无穷大与无穷小（重要）无穷小与无穷大的定义，它们之间的关系，以及与极限的关系（无穷小重要，无穷大了解）（例2不用看，定理2不用证明）习题1－4：1，6第五节：极限的运算法则（掌握）极限的运算法则(6个定理以及一些推论)（注意运算法则的前提条件是否各自极限存在）（定理1,2的证明理解，推论1,2,3，定理6的证明不用看）P46(例3,例4),P47(例6)习题1－5：1，2，3，4,5（重点）第六节：极限存在准则（理解）两个重要极限（重要）两个重要极限（要牢记在心，要注意极限成立的条件，不要混淆，应熟悉等价表达式，要会证明两个重要极限）,函数极限的存在问题（夹逼定理、单调有界数列必有极限），利用函数极限求数列极限，利用夹逼法则求极限，求递归数列的极限（准则1的证明理解，第一个重要极限的证明一定要会，另一个重要极限的证明不用看，柯西存在准则不用看）P51(例1)习题1－6：1，2，4第七节：无穷小阶的概念（同阶无穷小、等价无穷小、高无穷小的比较（重要）阶无穷小、k阶无穷小），重要的等价无穷小（尤其重要，一定要烂熟于心）以及它们的重要性质和确定方法（定理1,2的证明理解）P57(例1)P58(例5)习题1－7：全做9．理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型．10．了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质（有界性、最大值和最小值定理、介值定理），并会应用这些性质．第八节：函数的连续性与间断点（重要，基本必考小题）函数的连续性，间断点的定义与分类（第一类间断点与第二类间断点），判断函数的连续性（连续性的四则运算法则，复合函数的连续性，反函数的连续性）和间断点的类型。

考研数学常考知识点整理一、代数部分1.1 数学基础知识1.1.1 函数与方程1.1.1.1 基本函数与其性质1.1.1.2 方程与不等式1.1.2 数列与数列极限1.1.2.1 等差数列与等比数列1.1.2.2 数列极限的定义与性质1.1.3 概率与统计1.1.3.1 随机事件与概率计算1.1.3.2 排列组合与基本统计知识二、微积分部分2.1 极限与连续2.1.1 极限的定义与性质2.1.2 连续的概念与判定2.2 导数与微分2.2.1 导数的定义与性质2.2.2 微分的概念与计算2.3 积分2.3.1 不定积分与定积分的概念2.3.2 基本积分公式与常见积分方法2.3.3 几何应用与物理应用三、线性代数部分3.1 矩阵与行列式3.1.1 矩阵的基本运算与性质3.1.2 行列式的定义与计算3.2 向量空间与线性变换3.2.1 向量空间与子空间的概念3.2.2 线性变换的定义与性质四、概率论与数理统计部分4.1 随机变量与概率分布4.1.1 随机变量的定义与常见概率分布 4.1.2 期望与方差的计算4.2 参数估计与假设检验4.2.1 参数估计的方法与性质4.2.2 假设检验的基本原理与步骤五、常微分方程部分5.1 一阶常微分方程5.1.1 可分离变量与线性方程5.1.2 齐次方程与一阶线性方程 5.2 高阶常微分方程5.2.1 二阶常系数线性齐次方程5.2.2 二阶非齐次线性方程六、离散数学部分6.1 图论与树6.1.1 图的基本概念与性质6.1.2 树的定义与常见性质6.2 排列组合与离散概率6.2.1 排列与组合的基本计算6.2.2 离散概率的计算与应用以上是考研数学常考知识点的整理，希望对你的学习有所帮助。

记得多做练习题，夯实基础，理解概念及性质，注重对解题方法的掌握与应用。

加油！。

《高等数学部分》题型考点01极限的概念与性质【通用方法】极限与无穷小的关系：00lim (),()(1)x x f x A x x f x A o .题型考点02无穷小的比较（1）高阶无穷小、等价无穷小【通用方法】用定义转化成函数极限的计算问题.（2）无穷小排序【通用方法】利用0()lim0n x f x k x，解得n ，然后排序.题型考点03函数求极限【通用方法】（1）分析：把?x 代入极限，分析类型和化简方法（2）化简：①根式有理化②提公因子③计算非零因子④等价无穷小替换⑤拆分极限存在的项⑥幂指函数指数化⑦变量替换（尤其是倒代换）（3）计算：①洛必达法则②泰勒公式题型考点04极限的反问题（1）已知极限求另一极限【通用方法】加减乘除凑已知极限（2）已知极限求参数【通用方法】7种化简方法、泰勒公式、洛必达法则题型考点05函数的渐近线【通用方法】（1）垂直渐近线：若 )(lim x f ax ，则函数存在渐近线a x ；（2）水平渐近线：若b x f x)(lim ，则函数存在渐近线b y ；（3）斜渐近线：若b kx x f kx x f x x ])([lim )(lim ，则函数存在渐近线b kx y .题型考点06利用单调有界准则求数列极限【通用方法】（1）单调性①计算n n u u 1.若01 n n u u ，则}{n u 单调递增；若01 n n u u ，则}{n u 单调递减.②若)(1n n u f u ，构造函数)(x f ，单调数列应该有0)( x f ，若12u u ，则}{n u 单调递增；若12u u ，则}{n u 单调递减；另外，若0)( x f ，则数列不单调.（2）有界性①数学归纳法②均值不等式题型考点07求n 项和的数列极限【通用方法】①定积分定义②夹逼准则题型考点08判断函数的连续性与间断点【通用方法】①连续的定义②四种间断点的定义题型考点09一个点的导数【通用方法】一个点的导数用定义题型考点10切线方程与法线方程【通用方法】①求00(),()f x f x ②代入切线方程与法线方程.题型考点11各类函数求导（1）反函数求导【通用方法】反函数的导数等于原来函数导数的倒数.（2）复合函数求导【通用方法】从外层往内层逐层求导相乘.（3）隐函数求导【通用方法】把y 看成x 的函数，等式两边直接求导.（4）参数方程求导【通用方法】()()(),()()y t h t y h t y x t x t.（5）变限积分函数求导【通用方法】①设)()(21)()(x x dt t f x F，则)()]([)()]([)(1122x x f x x f x F ；②设xdt t xf x F 0)()(，则)()()()(00x xf dt t f dt t f x x F xx；注：被积函数中含有求导的变量时，要把变量分离出来，再求导.③设xdt t x f x F 0)()(，则令t x u ， xdu u f x F 0)()(，)()(x f x F .注：被积函数中含有求导的变量但不能直接分离时，要通过换元分离，再求导.（6）分段函数求导【通用方法】分段函数分段求，分段点处定义求题型考点12求0x 处的n 阶导数【通用方法】利用泰勒公式的唯一性题型考点13判断函数的单调性、极值点与凹凸性、拐点【通用方法】求函数的一阶导数、二阶导数进行判断题型考点14不等式的证明【通用方法】利用单调性证明（1）移项到大于号一边，构造()F x （2）求()()F x F x ,，判断()F x 的单调性（3）找()F x 的最小值点，验证最小值大于等于0.题型考点15方程根的问题【通用方法】①单调性②零点定理题型考点16曲率与曲率半径（仅数一、二要求）【通用方法】曲率公式232)1(y y K，KR 1.题型考点17罗尔定理的证明题【通用方法】（1）证明一阶导等于零（0)( f ），找两个原函数的点相等；（2）证明二阶导等于零（0)( f ），找三个原函数的点相等，或者两个一阶导相等；（3）证明表达式的题目（0)](),(,[ f f G ），思路如下：草稿纸上：① 换成x 把要证明的表达式抄下来；②两边移项，目的是便于积分求原函数注：遇到)(x f 可以把它除到)(x f 下面去，积分为)(ln x f ；③两边积分，目的是构造有用的)(x F 试卷上：令 )(x F ，易知)(x F 在],[b a 上连续，),(b a 内可导，再证明)(x F 两个点相等即可.（4）双介值问题：解题思路：①分离介值，把含不同介值的表达式移到等号两边；②结合（3）的思路，分别使用微分中值定理证明左边C ，右边C 即可注：C 为某常数，需要通过其中一边C ，满足罗尔定理的情况下，求得.另外，若只是证明存在两个介值，则不需要把区间分段；若要求证明存在两个不同的介值，则必须把区间分段，证明介值分别来自两个不同的区间.题型考点18拉格朗日中值定理的证明题【通用方法】找对区间（一般需要将区间等分或者根据第一问提示点将区间分开），在各区间上使用拉氏定理，然后相加相减凑所证结论.题型考点19泰勒中值定理的证明题【通用方法】找对展开点（一般为区间中点或端点），然后写出泰勒展开式，带入端点值，相加相减凑所证结论.题型考点20不定积分的计算【通用方法】①凑微分②去根号③分部积分④有理函数积分题型考点21定积分的计算【通用方法】①牛顿莱布尼兹公式②定积分的换元法③区间再现④分段函数分段积分⑤含抽象函数的积分使用分部积分题型考点22积分不等式的证明【通用方法】①转化为函数不等式，利用单调性证明②积分中值定理题型考点23含变限积分函数的等式方程【通用方法】①初值②求导题型考点24反常积分的计算【通用方法】在瑕点处拆开，直接按定积分计算.题型考点25反常积分敛散性的判定【通用方法】根据比较审敛法的极限形式，与P 积分进行比较判断.题型考点26定积分的几何应用【通用方法】微元法（1）求平面图形的面积① dxx y x y S ba121② d r S2221③dtt t ydx S ba3（2）求旋转体的体积① dxx fV bax2②bay dxx xf V2③d y V Dx（3）求平面曲线的弧长d r r dt t y t x dxx y ds 222221（仅数一、二要求）（4）求旋转体的侧面积ydsd S 2 侧（仅数一、二要求）题型考点27定积分的物理应用（仅数一、二要求）【通用方法】微元法（1）变力沿曲线做功①FSW ②maF （2）静水侧压力①PS F ②ghP（3）引力问题①221r m m GF 万②221r Q Q kF 库题型考点28微分方程的求解【通用方法】根据各类微分方程的固定求解步骤进行即可.（1）一阶微分方程①可分离变量的方程②齐次方程③一阶线性微分方程（2）可降阶的微分方程①不显含y 的微分方程②不显含x 的微分方程（3）二阶常系数线性微分方程①二阶常系数线性齐次方程②二阶常系数线性非齐次方程（4）伯努利方程、欧拉方程（仅数一）通过换元化为常见方程求解题型考点29微分方程的物理应用（仅数一、二要求）【通用方法】从问题出发，找两个变量，列微分方程.题型考点30多元复合函数求偏导【通用方法】①画出复合函数关系图②从外往内逐层求偏导题型考点31多元隐函数求偏导【通用方法】①直接求②公式法③一阶微分形式不变性（全微分法）题型考点32偏积分【通用方法】注意对x 积分时加)(y C ，对y 积分时加)(x C .题型考点33多元函数极值【通用方法】①令偏导数等于0解得驻点②根据充分条件判断极值题型考点34多元函数条件极值【通用方法】①代入法②拉格朗日乘数法题型考点35多元函数求闭区域上的最值【通用方法】①开区域内求极值②边界上求条件极值③比大小题型考点36各类积分比大小【通用方法】①不等式性质②对称性③格林公式、高斯公式（仅数一）题型考点37二重积分的计算【通用方法】①画D②观察对称性③选择坐标系和积分次序④化为累次积分计算题型考点38数项级数敛散性的判断（仅数一、三）【通用方法】（1）正项级数①比较审敛法（极限形式）②比值（根植）审敛法（2）交错级数①加绝对值后判断是否绝对收敛②莱布尼兹判别法（3）一般级数①加绝对值后判断是否绝对收敛②级数敛散性的性质题型考点39幂级数的收敛域及和函数（仅数一、三）【通用方法】（1）收敛域比值法（2）和函数逐项积分，逐项求导（3）函数展开成幂级数①逐项积分，逐项求导②常见泰勒级数题型考点40函数展开成傅里叶级数（仅数一）【通用方法】（1）周期为 2的傅里叶级数①10sin cos 2~)(n n n nx b nx a a x f ，其中,2,1,sin )(1,)(1,2,1,cos )(1n nxdx x f b dx x f a n nxdx x f a n n.②余弦级数若)(x f 为偶函数，则10cos 2~)(n n nx a a x f ，其中.0,)(2,2,1,cos )(200n n b dx x f a n nxdx x f a③正弦级数若)(x f 为奇函数，则1sin ~)(n nnx bx f ，其中,2,1,sin )(2,2,1,0,00n nxdx x f b n a n n（2）周期为l 2的傅里叶级数10sincos 2~)(n n n lxn b l x n a a x f ，其中 l l n l l n dx lxn x f l b dx l x n x f l a sin )(1,cos )(1.（3）狄里克雷收敛定理设)(x f 是周期为 2的可积函数，且满足①)(x f 上],[ 连续或只有有限个第一类间断点；②)(x f 上],[ 只有有限个单调区间，则)(x f 的以 2为周期的傅里叶级数收敛，且2)0()0()(000x f x f x S .题型考点41空间解析几何（仅数一）【通用方法】（1）平面与直线①平面点法式②直线点向式（2）曲面与曲线①旋转曲面轨迹法②投影曲线消元法（3）空间曲面的切平面与空间曲线的切线①曲面的法向量),,(z y x F F F ②曲线的切向量))(),(),((t z t y t x 或))(),(,1(x z x y 等.题型考点42三重积分的计算（仅数一）【通用方法】①投影法②截面法③柱面坐标④球面坐标题型考点43曲线积分的计算（仅数一）【通用方法】（1）第一类曲线积分①对称性②参数法（2）第二类曲线积分①对称性②参数法③积分与路径无关④格林公式题型考点44曲面积分的计算（仅数一）【通用方法】（1）第一类曲面积分①对称性②一投二代三计算（2）第二类曲面积分①对称性②一投二代三定号③轮换投影法④高斯公式题型考点45多元积分学的应用（仅数一）【通用方法】（1）质心、形心①质心横坐标D Dd y x f d y x xf x),(),(；dVz y x f dV z y x xf x ),,(),,(；LL dsy x f ds y x xf x ),(),(；dSz y x f dS z y x xf x ),,(),,(.②形心横坐标（数二、三的同学要求掌握平面图形的形心）DDd xd x；dVxdV x ；L Ldsxds x ；dSxdSx .（2）转动惯量2mr I 题型考点46场论公式（仅数一）【通用方法】（1）方向导数①定义),()cos ,cos (lim 00000y x f y x f l.②可微函数cos cos y x f f l.（2）梯度),(),(y x f f y x gradf （3）散度zR y Q x P A div（4）旋度Qy j A rot题型考点47经济学应用（仅数三）【通用方法】（1）边际)(x f dxdy（2）弹性xdx y dy E yx《线性代数部分》题型考点01数值型行列式的计算【通用方法】边化零，边展开题型考点02抽象行列式的计算【通用方法】①化为乘法②特征值的乘积题型考点03方阵的幂【通用方法】（1）找规律（2）若1)( A r ，则A A 1n nl，其中)(A tr l .（3）若1A P ΛP ，则P ΛP A nn1.题型考点04矩阵的秩【通用方法】①化行阶梯形②利用秩的9个结论题型考点05具体方程组的求解【通用方法】①化行阶梯形②化行最简形③写出同解方程组④写出通解题型考点06抽象方程组的求解【通用方法】解的结构（1）齐次方程组的基础解系：①是解②无关③个数()n r A （2）非齐次方程组的通解： 通通特非齐非题型考点07向量组的线性相关性【通用方法】①秩②定义题型考点08向量组的线性表示【通用方法】①秩②定义题型考点09向量组的极大无关组【通用方法】①部分组②无关③个数()r A .题型考点10相似对角化【通用方法】（1）解0 E A 得特征值123,, ；（2）解()0x E A 得特征向量123,,ααα；（3）令123(,,) P ααα，则1P AP Λ.题型考点11正交变换法化二次型为标准形【通用方法】（1）解0 E A 得特征值123,, ；（2）解()0x E A 得特征向量123,,ααα；（3）正交化得：123,,βββ；（4）单位化得：123,,γγγ；（5）令123(,,) Q γγγ，则在正交变换x y Q 下，二次型的标准形为222112233y y y .题型考点12配方法化二次型为标准形【通用方法】①优先配交叉项少的变量②所用变换必须为可逆变换题型考点13二次型的正定型【通用方法】等价条件：①0,0Tx x x A ；②特征值均大于0；③正惯性指数为n ；④顺序主子式均大于0.《概率统计部分》题型考点01概率计算公式【通用方法】（1）加法公式()P A B C 加奇减偶（2）减法公式()()()P AB P A P AB （3）乘法公式()(|)()(|)()P AB P A B P B P B A P A （4）条件概率()(|)()P AB P A B P B（5）全概率公式1()(|)()nk k k P A P A B P B （6）贝叶斯公式(|)()(|)()k k k P A B P B P B A P A题型考点02概率密度与分布函数【通用方法】（1）概率密度①()1f x dx；(,)1xoyf x y d ②()0f x ；(,)0f x y （2）分布函数①规范性()0,()1F F ②右连续性00(0)()F x F x ③单调不减性题型考点03常见分布【通用方法】题型考点04二维连续型随机变量的分布【通用方法】（1）边缘概率密度()(,),()(,)X Y f x f x y dy f y f x y dx（2）条件概率密度(,)()()X Y Y f x y f x y f y（3）独立性若(,)()()X Y f x y f x f y ，则,X Y 独立（4）事件概率{(,)}(,)DP X Y D f x y d题型考点05随机变量函数的分布【通用方法】（1）一维连续型随机变量函数的概率密度分布函数法：①定义②代入③讨论④求导（2）一维连续型随机变量函数的概率密度分布函数法：①定义②代入③讨论④求导公式法：()(,(,))Z y f z f x y x z dx z（3）离散型+连续型随机变量函数的概率密度分布函数法：①定义②代入③全概率公式④讨论⑤求导题型考点06数字特征【通用方法】（1）随机变量的数字特征①期望 取值概率②方差性质化简，公式计算③协方差性质化简，公式计算④相关系数性质化简，公式计算（2）统计量的数字特征①E X EX②1D X DX n③2ES DX④2()E n n⑤2()2D n n题型考点07二维正态分布的性质【通用方法】若221212(,)~(,;,;)X Y N ，则：（1）边缘分布都是服从一维正态分布，即 221122~,,~,X NY N .（2）X 和Y 任意的非零线性组合aX bY 服从一维正态分布.（3）X 和Y 相互独立的充要条件是相关系数0 .（4）若12,Z Z 是,X Y 的非零线性组合，则 12,Z Z 也服从二维正态分布.题型考点08三大抽样分布【通用方法】（1）2分布：222212()nn X X X （2）F 分布：22()(,)()m mF m n n n（4）t 分布：()t n（5）若12,,,n X X X 为来自正态总体2~(,)X N 的简单随机样本，则：~(0,1)X N②222(1)~(1)n S n ~(1)X t n 题型考点09点估计【通用方法】（1）矩估计总体的矩等于样本的矩（2）最大似然估计①离散型1()()n i i L P X X ；1()ln(())ni i LnL P X X ②连续型1()()ni i L f x ；1()ln(())ni i LnL f x 题型考点10估计量的评选标准【通用方法】（1）无偏性 ()E（2）有效性若 12()()D D ，则 1 比 2更有效（3）一致性P。

2021年考研数学大纲：数学二考试范围
我们先来看看数二不考的内容：三重积分，曲线曲面积分，无穷
级数（包括傅里叶级数），向量代数与空间解析几何，多元函数微分
学中方向导数和梯度、空间曲线的切线和法平面及曲面的切平面和法线，导数的经济应用，定积分的经济应用，无界区域上简单的反常二
重积分，常微分方程中的伯努利方程、全微分方程、可用简单的变量
代换求解的某些微分方程、欧拉方程、差分方程。

数学二考的内容有：导数应用中的曲率和曲率圆，导数的物理应用，定积分中有理函数的积分、三角函数的有理式积分、简单无理函
数的积分，旋转体的侧面积与曲线弧长，平行截面积为已知的立体体积，定积分的物理应用（功，引力，压力，质心，形心等），可降阶
的微分方程，高于二阶的某些常系数齐次线性方程，微分方程的物理
应用。

这里没有提到的都是数学一二三共同考的，就不在赘述了，希望
能够协助到你。

知道了这数二需要考试的范畴，就请数二的小朋友收起你的开心，安静的实行本阶段应该的复习规划，对于本阶段需要仔细研究历年考
研真题，研究的过程中需要完成两个大任务，第一：完善自己的知识
框架，构建完成的知识体系，在暑期的复习中我们已经对数学每一部
分的知识点和题型有所了解，并且掌握了不同类题型的做题思路，还
不能够系统的搭建知识体系，所以本阶段就需要完成这个任务，协助
我们从整理来把握数学的知识点；第二，扩展考研题型，解决考研题
型的解题思路，在做历年真题的时候，我们会遇到自己以前没有遇到
过的题型，或者不知道一个知识点还能够跟这样的题联系在一起，所
以在这个阶段就将它们一举拿下。

快快复习吧！。

本科学年论文论文题目：积分在计算物体体积和质量等问题中的应用学生XX：学号：专业：班级：指导教师：完成日期：2011年12 月20 日目录内容摘要1关键词1序言2一、定积分的微小元素法31、内容要点32、曲边梯形的面积计算方法，定积分的定义43、计算面积的元素法步骤：4二、空间立体的体积41、平行截面面积为已知的立体体积42、旋转体的体积7三、重积分在几何中的应用10四、重积分在物理学中的应用111、三重积分的概念122．三重积分的定义133、三重积分的物理意义：134、三重积分的性质14五、质量14参考文献16积分在计算物体体积和质量等问题中的应用内容摘要掌握定积分计算基本技巧；并用所学的定积分的微元法（元素法）去解决各种领域中的一些实际问题；掌握用定积分表达和计算一些几何量与物理量（旋转体的体积平行截面面积为已知的立体体积等）。

对于重积分的计算其基本思想是将重积分化为累次积分进行计算.本文首先给出如何应用定积分的微元法（元素法）再到运用定积分解决实际问题，最后引出二重积分，三重积分。

再通过例子研究积分性质在计算实际问题中的应用.关键词：积分体积质量定积分序言用找出未知量的元素（微元）的方法建立这些几何、物理的公式解决实际问题。

运用元素法将一个量表达为定积分的分析方法是解决积分问题的重要思想。

而重积分是一元函数定积分的推广，是多元函数积分学的重要组成部分，在几何学与物理学中都得到了广泛的应用.在几何上，重积分可用来求空间曲面的面积、求空间区域的体积.在物理上，重积分可用来求物体的质量等.但与定积分相比较，重积分的计算除了与被积函数的结构有关外，更大程度上与积分区域的特点有关.下面就针对积分对于计算物体体积和质量的问题进行分析.一、定积分的微小元素法1、内容要点定积分概念的引入，体现了一种思想，它就是：在微观意义下，没有什么“曲、直”之分，曲顶的图形可以看成是平顶的，“不均匀”的可以看成是“均匀”的。

关于考研数学复习计划(系列)考研数学复习计划(篇1)主要任务：将强化阶段所学知识进行归纳和整理，有效形成系统。

总结在上一阶段的复习过程中遇到的问题，并一一解决。

做真题，以知识点为内容进行分类练习。

反思自问：知识层面达到什么样的高度?知识点掌握的程度如何?此时你的知识水平距离考试的要求还有多远?重点掌握:在这一阶段的复习中，大家至少要掌握极限、导数、不定积分这三方面的内容，才能在接下来的复习中有好的收效。

x月的前半个月，我们应该怎么对强化阶段做一个良好的收尾呢。

第一，复习方法采用“两端看法”,就是对强化阶段的所学过的知识和做题方法做一个总结和归纳。

总结和归纳结束之后，采用高等数学、概率论一起交叉、轮流来看，最后汇集到线性代数上。

我们也把这个阶段用一个字来形容“啃”，所以也可以叫做“啃”强化阶段所学过到的知识。

这里的“啃”是来形容这个阶段的艰难程度，大家到了这个阶段普遍感到压力陡增，即使那些在第一阶段认真完成的同学也一样，这里的主要原因是这一阶段大家所学到的知识和解题方法普遍特点是对知识点的总结是高度的概括的，虽然老师在强化阶段帮助大家将知识体系化和系统化，但是那毕竟是老师的东西，考生应该学着将这些东西变成自己的。

第二，所选的题目不论是例题还是课后的练习题都具有一定的综合性，这些题目不再是只考查单一的知识点，单一的解题能力，而是对同学们能力的全方位考查，不仅考查同学们的计算能力、抽象概括能力、空间想象能力还考查同学们应用所学的知识解决实际问题的能力。

大家在平时练习的时候做适量难度稍大的题，会有助于大家在考试过程中保持平和的心态，遇到难题不会慌。

但这并不是说让大家在复习的过程中就只钻研难题，而对于容易的题和中等难度的题不屑一顾，这样只会导致考研失败。

我们做题难度要适当，题量要适当。

所以，大家不要进入做题的误区，要难度适当地练习，不要死扣难题，毕竟考研考察的是基础知识，使大家都能接受的水平。

这就要求同学们在这个阶段付出巨大的努力，但是无论你多累都是值得的，通过这个阶段洗礼，无论是你对三基的掌握程度，还是你的解题能力都会有质的提高。

考研数学基础知识点梳理(高数篇) 第一章函数、极限与连续1、函数的有界性2、极限的定义(数列、函数)3、极限的性质(有界性、保号性)4、极限的计算(重点)(四则运算、等价无穷小替换、洛必达法则、泰勒公式、重要极限、单侧极限、夹逼定理及定积分定义、单调有界必有极限定理)5、函数的连续性6、间断点的类型7、渐近线的计算第二章导数与微分1、导数与微分的定义(函数可导性、用定义求导数)2、导数的计算(“三个法则一个表”：四则运算、复合函数、反函数，基本初等函数导数表;“三种类型”：幂指型、隐函数、参数方程;高阶导数)3、导数的应用(切线与法线、单调性(重点)与极值点、利用单调性证明函数不等式、凹凸性与拐点、方程的根与函数的零点、曲率(数一、二)) 第三章中值定理1、闭区间上连续函数的性质(最值定理、介值定理、零点存在定理)2、三大微分中值定理(重点)(罗尔、拉格朗日、柯西)3、积分中值定理4、泰勒中值定理5、费马引理第四章一元函数积分学1、原函数与不定积分的定义2、不定积分的计算(变量代换、分部积分)3、定积分的定义(几何意义、微元法思想(数一、二))4、定积分性质(奇偶函数与周期函数的积分性质、比较定理)5、定积分的计算6、定积分的应用(几何应用：面积、体积、曲线弧长和旋转面的面积(数一、二)，物理应用：变力做功、形心质心、液体静压力)7、变限积分(求导)8、广义积分(收敛性的判断、计算)第五章空间解析几何(数一)1、向量的运算(加减、数乘、数量积、向量积)2、直线与平面的方程及其关系3、各种曲面方程(旋转曲面、柱面、投影曲面、二次曲面)的求法第六章多元函数微分学1、二重极限和二元函数连续、偏导数、可微及全微分的定义2、二元函数偏导数存在、可微、偏导函数连续之间的关系3、多元函数偏导数的计算(重点)4、方向导数与梯度5、多元函数的极值(无条件极值和条件极值)6、空间曲线的切线与法平面、曲面的切平面与法线第七章多元函数积分学(除二重积分外，数一)1、二重积分的计算(对称性(奇偶、轮换)、极坐标、积分次序的选择)2、三重积分的计算(“先一后二”、“先二后一”、球坐标)3、第一、二类曲线积分、第一、二类曲面积分的计算及对称性(主要关注不带方向的积分)4、格林公式(重点)(直接用(不满足条件时的处理：“补线”、“挖洞”)，积分与路径无关，二元函数的全微分)5、高斯公式(重点)(不满足条件时的处理(类似格林公式))6、斯托克斯公式(要求低;何时用：计算第二类曲线积分，曲线不易参数化，常表示为两曲面的交线)7、场论初步(散度、旋度)第八章微分方程1、各类微分方程(可分离变量方程、齐次方程、一阶线性微分方程、伯努利方程(数一、二)、全微分方程(数一)、可降阶的高阶微分方程(数一、二)、高阶线性微分方程、欧拉方程(数一)、差分方程(数三))的求解2、线性微分方程解的性质(叠加原理、解的结构)3、应用(由几何及物理背景列方程)第九章级数(数一、数三)1、收敛级数的性质(必要条件、线性运算、“加括号”、“有限项”)2、正项级数的判别法(比较、比值、根值，p级数与推广的p级数)3、交错级数的莱布尼兹判别法4、绝对收敛与条件收敛5、幂级数的收敛半径与收敛域6、幂级数的求和与展开7、傅里叶级数(函数展开成傅里叶级数，狄利克雷定理)。

考研数学十二章知识点归纳考研数学是许多学生在准备研究生入学考试时的重点科目。

以下是对考研数学十二章知识点的归纳总结：第一章：极限与连续- 极限的定义和性质- 无穷小量的阶- 连续性的定义和性质- 闭区间上连续函数的性质第二章：导数与微分- 导数的定义和几何意义- 基本导数公式- 高阶导数- 隐函数和参数方程求导- 微分的定义和应用第三章：中值定理与导数的应用- 罗尔定理、拉格朗日中值定理和柯西中值定理- 泰勒公式- 导数在几何上的应用：曲线的切线、法线和弧长- 导数在物理上的应用：速度、加速度等第四章：不定积分- 不定积分的定义和性质- 基本积分公式- 换元积分法和分部积分法- 有理函数的积分第五章：定积分- 定积分的定义和性质- 牛顿-莱布尼茨公式- 定积分的计算方法- 定积分在几何和物理上的应用第六章：多元函数微分法- 偏导数和全微分- 多元函数的极值问题- 条件极值和拉格朗日乘数法第七章：重积分- 二重积分和三重积分的定义- 积分区域和积分顺序- 重积分的计算方法：直角坐标系、极坐标系和球坐标系第八章：曲线积分与曲面积分- 第一类和第二类曲线积分- 格林公式和斯托克斯定理- 高斯公式和奥斯特罗格拉德斯基定理第九章：无穷级数- 常数项级数的收敛性- 幂级数和泰勒级数- 函数的幂级数展开- 傅里叶级数和傅里叶变换第十章：常微分方程- 一阶微分方程的解法：分离变量法、变量替换法、常数变易法- 高阶微分方程的降阶- 线性微分方程的解法：特征方程法、常系数线性微分方程第十一章：偏微分方程- 偏微分方程的基本概念- 一阶偏微分方程的解法- 热传导方程、波动方程和拉普拉斯方程第十二章：线性代数- 向量空间和线性变换- 矩阵的运算和性质- 行列式和逆矩阵- 特征值和特征向量- 二次型和正定矩阵结束语：考研数学的知识点广泛，需要同学们系统地学习和大量的练习。

希望以上的归纳能够帮助大家更好地复习和掌握考研数学的主要内容。

考研数学定积分的物理应用分析
在考研数学中,对于数学(一)和数学（二）的考生来说，考试大纲要求掌握一些定积分的物理应用，主要包括:做功、压力、引力、质心、形心等，这是因为数学（一)和数学（二）的大部分考生是理工科专业的学生，因此要求掌握一些物理应用是十分合理和自然的定积分在作用力做功计算中的应用
定积分在压力计算中的应用
从上面的分析和典型例题来看，求解定积分的物理应用问题时，首先要掌握相应的物理基本原理，这是最基本、同时也是最重要的前提条件，如果不理解其物理原理，则应用就无从谈起。