当前位置：文档之家 › 53定积分的换元法和分部积分法习题

53定积分的换元法和分部积分法习题

  • 格式：doc
  • 大小：3.29 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

定积分的换元积分法与分部积分法

定积分的换元积分法与分部积分法

有
b
a f (x) dx f [(t)](t) dt
上式称为定积分的换元公式。
π
例1 计算 2 cos3 x sin x dx 。 0
解
设 t cos x ，则 dt sin x dx 。当 x 0 时，t 1 ；当
x π 时，t 1。 2
原式 0 t3dt 1 t3dt 1 t4计算
4 dx 。
0 1 x
解
令 x t ，x t2 ，则 dx 2tdt 。当 x 0 时，t 0 ；当
x 4 时，t 2。
原式 2 2t dt 2 2 t 1 1 dt 2 2 ln 1 t 2 4 2ln 3
0 1t
0 1t
0
例3 计算
高等数学
定积分的换元积分法与分 部积分法
一、定积分的换元积分法
定理 设函数 f (x) 在 [a ，b] 上连续，而 x (t) 是定义在 [ ， ] 上的一个可微函数，并满足条件：
（1）(t)在区间 [a ，b] 上有连续的导数 (t) ；
（2）当t从α 变到β 时，(t) 从 ( ) a 单调地变到( ) b ，则
两边积分，得 移项，得 即
b
b
b
a (uv)dx a uvdx a uvdx
b uvdx
(uv)
b
b
vudx
a
a
a
b
b
b
udv uv vdu
a
a
a
这就是定积分的分部积分公式。
π
例6 计算 0 x cos x dx 。
解
原式
π
xd (sin
x)
x sin x
π
π

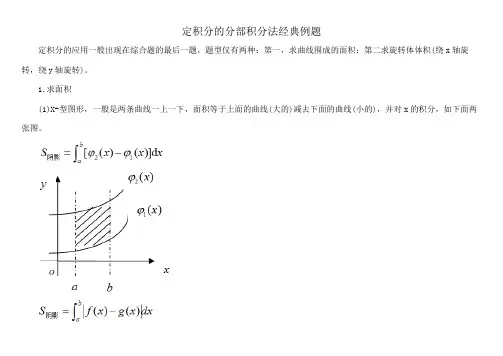
定积分的分部积分法经典例题

定积分的分部积分法经典例题

定积分的分部积分法经典例题
定积分的应用一般出现在综合题的最后一题，题型仅有两种：第一，求曲线围成的面积；第二求旋转体体积(绕x轴旋转，绕y轴旋转)。

1.求面积
(1)X-型图形，一般是两条曲线一上一下，面积等于上面的曲线(大的)减去下面的曲线(小的)，并对x的积分，如下面两张图。

求面积首要问题是画出草图，图形的上下位置(或者左右位置)，交点一定要做得准确。

通常曲线，例直线、抛物线、双曲线、指数、对数、三角函数的图像要画得熟练、准确。

求出结果后要检验，这样的题型是一个实际问题，所得结果要合乎逻辑。

(2)Y-型，一般是两条曲线一左一右，面积等于右边的曲线(大的)减去左边的曲线(小的)，并对y的积分，如下图
2.旋转体体积
求旋转体体积时要充分发挥几何空间想象能力，要想象出旋转出的体积大概是什么形状的。

(1)X-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
(2)Y-型图形
绕x轴旋转所得图形的体积
绕y轴旋转所得图形的体积
常考题型如下：。

【2019年整理】定积分的换元法与分部积分法99169

【2019年整理】定积分的换元法与分部积分法99169

四、设 f ( x)在 a , b 上连续，
证明
b
f ( x)dx
b f (a b x)dx.
a
a
五、证明：
1 x m (1 x)n dx 1 x n (1 x)m dx .
0
0`
上页 下页 返回
六、证明：
a f ( x)dx
a
[ f (x)
f ( x)]dx,
a
0
并求
0
0
（2）设 x t dx dt,
x 0 t ,
x t 0,
0
0 xf (sin x)dx ( t) f [sin( t)]dt
0 ( t) f (sin t)dt,
上页 下页 返回
0 xf (sin x)dx 0 f (sin t)dt 0 tf (sin t)dt
解 令 u arcsin x, dv dx,
则 du dx , v x, 1 x2
1
2 arcsin xdx
0
x
arcsin
1
x2 0
1 2
0
1
1
1 2
2 6 20
1 d(1 x2 ) 1 x2
xdx 1 x2
12
1
1 x2
2
0
3 1.
12 2
上页 下页 返回
3
x
3
)dx
___________________；
2、 (1 sin3 )d ________________； 0
3、 2 2 x 2 dx _____________； 0
4、
1 (arcsin x)2
2
1
2
1 x2

定积分的换元法和分部积分法

定积分的换元法和分部积分法

10
1 1 ( x)2
d( x) 2
arcsin
x 2
1 0
π 2
2
例3
计算
02
sin6xcosxdx
解
02
sin6xcosxdx02
sin6xd(sinx)
π
sin
7x
2
7 0
1 7
例4
计算
1e
1 lnx x
dx
解
e 1
1 lnx dx x
e1(1lnx)d(1lnx)
(1
ln
1
1
解法1
2 0
arcsinxdx
02arcsixnd(x)
1 1 xdx
xarcsixn02
2 0
1 x2
1 26
1
1 2
20
1 d(1x2) 1x2
12
1
1x2
2
0
31.
12 2
解法2
1
02arcsixndx
换 元t： arcsxin
6td(sitn)
则xsin t 0
分 部 积 分
2. 第二类换元积分法
设函数 f ( x) 在区间 [a, b] 上连续 ，函数 xφ(t)
满足 (1) φ(α)a, φ(β)b
(2) φ(t)在 [α, β]（或 [β, α]）上具有连续
导数，且 φ(t)[a, b] ，于是
a bf(x)dx βf[φ(t)φ ](t)dt
注意: （1）换元前后，上限对上限、下限对下限；
2
t
3
2 t
3 1
8 3
例7
计算
04

(5.3) 第三节 定积分换元法和分部积分法(少学时简约版)

(5.3) 第三节 定积分换元法和分部积分法(少学时简约版)

b
因此不定积分分项积分法则可直接转换为定积分的
分项积分法则。
(2) 凑微分法则的转换 若 f( x )有原函数 F( x )，( x )可微，则有不定积 分凑微分法则 ∫ f[( x )] ( x )d x = ∫ f[( x )]d ( x )
= ∫ d F[( x )]= F[( x )]+ C .
t x
x
x
x 0
f u d u tf t d t xf t d t tf t d t 0 0 0
x
x
x
f t x t d t . 0
尽管利用牛顿―莱布尼茨公式定积分可通过不定 积分计算，但其间却存在一个问题，因为定积分和不定 积分在概念上不是一回事。定积分是和式极限，只要被 积函数连续，定积分就可积。不定积分是原函数簇，其

3 0
x2 dx 1 x
3
5 3 76 . 1 2 2 1 x 1 x 1 x 5 0 15 3
不定积分计算目的在于求原函数，当积分变量改 变后，原函数形式也相应发生改变。为求得对应于给 定积分变量的原函数形式，用第二换元法求不定积分

f x d x f x d x f x d x . a a 0
a
0
a
为比较两部分积分，考虑将它们化为同一区间上
的积分考察。
对第一个积分作代换 x = - t ，当 x :- a 0 时，t : a 0,
需作原变量回代，而原变量回代涉及代换函数 x = ( t )
的反函数计算，故第二换元法一般计算比较繁杂。 定积分计算的目的在于求值，积分变量的改变对 定积分计算并不显得特别重要。因为当积分变量改变 后，其相应的变化范围也随之改变，因此只要能确定

5.3 定积分的换元法和分部积分法-习题

5.3 定积分的换元法和分部积分法-习题

1．计算下列定积分： ⑴3sin()3x dx πππ+⎰；【解法一】应用牛顿-莱布尼兹公式3sin()3x dx πππ+⎰3sin()()33x d x ππππ=++⎰3cos()3x πππ=-+[cos()cos()]333ππππ=-+-+[cos (cos )]033ππ=----=。

【解法二】应用定积分换元法令3x u π+=，则d x d u =，当x 从3π单调变化到π时，u 从23π单调变化到43π，于是有3sin()3x dx πππ+⎰4323sin udu ππ=⎰4323cos uππ=-42[coscos ]33ππ=-- [cos(cos )]033ππ=----=。

⑵132(115)dxx -+⎰；【解法一】应用牛顿-莱布尼兹公式132(115)dx x -+⎰1321(115)(115)5x d x --=++⎰21211(115)52x --=⋅+-22111[]10(1151)(1152)=--+⨯-⨯211(1)1016=--51512=。

【解法二】应用定积分换元法令115x u +=，则15dx du =，当x 从2-单调变化到1时，u 从1单调变化到16，于是有132(115)dxx -+⎰163115u du -=⎰21611152u -=⋅-211(1)1016=--51512=。

⑶32sin cos d πϕϕϕ⎰；【解法一】应用牛顿-莱布尼兹公式320sin cos d πϕϕϕ⎰32cos cos d πϕϕ=-⎰4201cos 4πϕ=-441[cos cos 0]42π=--1[01]4=--14=。

【解法二】应用定积分换元法令cos u ϕ=，则sin d du ϕϕ-=，当ϕ从0单调变化到2π时，u 从1单调变化到0，于是有320sin cos d πϕϕϕ⎰031u du =-⎰130u du =⎰4114u =14=。

⑷30(1sin )d πθθ-⎰；【解】被积式为3(1sin )d θθ-，不属于三角函数的基本可积形式，须进行变换。

5.3 定积分的换元法和分部积分法

5.3 定积分的换元法和分部积分法
( 2 ) න (sin )d
= − න (π − )(sin(π − ))d
则 d = −d
0
0
π
= න (π − )(sin )d
0
π
π
= π න (sin )d − න (sin )d
0
π
0
π
= π න (sin )d − න (sin )d ,
0​
​
+ න () d
0​
= න [(−) + ()] d
0​
​
2 න () d , (−) = (),
=
0​
0,
− = − .
奇、偶函数在对称区间上的定积分性质 偶倍奇零
第三节 定积分的换元法和分部积分法
定积分
第五章
1
2 2 + cos
例6 计算 න
0
解
1
d.
( > 0)
π
令 = sin , d = cos d, = ⇒ = , = 0 ⇒ = 0.
2
π
2
cos
d
原式 = න
2
2
0 sin + (1 − sin )
=න
π
2
0
cos
1
d = න
sin + cos
1
=
6
6
1
อ
第三节 定积分的换元法和分部积分法
0
cos 5 sin d
= − න cos 5 d(cos )
= 0 ⇒ = 1.
原式 = − න
π
2
1
= .

5-3定积分的换元法与分部法-精品文档

5-3定积分的换元法与分部法-精品文档
2


1 ( 1 cos 2 t)d t cos t d t 2
2
1 1 t sin 2t 2 arcsin x x1 x C C 2 2 2 4
由牛顿 莱布尼兹公式 ， 得
1 1 1 2 1 x d x arcsin x x 1 x . 0 2 2 0 4 1 2
0
a
x ) d x [ f ( x ) f ( x )] d x . f(
a 0
a
a
( 1 )若 f ( x ) 为偶函数，则 f ( x ) f ( x ) ，故有

a
a
f (x)dx 2

a
0
f (x)d x
( 2 ) 若 f ( x ) 为奇函数，则 f ( x ) － f ( x ) ，故
1
1 2 2 1 2 2 sin xcos xdx sin xdsin x sin x |0 0 0 2 2


例5
设 f(x ) 在对称区间 [ a ,a ]上连续，证明：
( 1 ) 当 f ( x ) 为偶函数时， x ) d x 2 x ) d x . f( f(

f (x)dx f ( t)(dt) f ( x )dx. t)dt f( a a
0
0
0
0
a
a
于是
( x ) d x f ( x ) d x f ( x ) d x f
a 0 0
a
a
a
x ) f( x )] d x . [f(
则
定理证明 定理证

b

高数53换元法与分部积分法

高数53换元法与分部积分法
注意积分技巧
在运用换元法和分部积分法时，需要注意一些积分技巧，如选择合适的代换变量、合理拆分被积函数等。这 些技巧可以帮助我们更有效地求解复杂积分。
04 复杂函数求解技巧与实例 分析
复杂函数类型及特点
01
02
03
复合函数
由多个基本初等函数通过 四则运算或复合而成的函 数，如$f(g(x))$。
隐函数
THANKS FOR WATCHING
感谢您的观看
高数53换元法与分部积分法
目录
• 换元法基本概念与原理 • 分部积分法基本概念与原理 • 换元法与分部积分法关系探讨 • 复杂函数求解技巧与实例分析 • 实际应用问题中换元和分部积分思想体现 • 总结回顾与拓展延伸
01 换元法基本概念与原理
换元法定义及作用
换元法是一种通过变 量代换简化复杂数学 表达式或方程的方法。
解。
06 总结回顾与拓展延伸
关键知识点总结回顾
换元法
通过变量代换将复杂积分转化为简单积分，包括第一类换元法（凑微分法）和第 二类换元法（三角代换、根式代换等）。
分部积分法
将复杂被积函数拆分成两个简单函数的乘积，通过求导和积分降低计算难度，特 别适用于含有幂函数、指数函数、三角函数等基本初等函数的积分。
易错点剖析及注意事项
换元法易错点
在换元过程中，需要注意新变量 的取值范围与原变量保持一致， 同时在最后要将结果代换回原变
量。
分部积分法易错点
在选择u和dv时，需要遵循“反对 幂指三”的优先级顺序，同时要注 意计算过程中的符号变化。
注意事项
在应用换元法和分部积分法时，需 要熟练掌握基本初等函数的求导和 积分公式，以便进行正确的代换和 拆分。

定积分换元法与分部积分法习题

定积分换元法与分部积分法习题

1．计算下列定积分： ⑴3sin()3x dx πππ+⎰；【解法一】应用牛顿-莱布尼兹公式3sin()3x dx πππ+⎰3sin()()33x d x ππππ=++⎰3cos()3x πππ=-+[cos()cos()]333ππππ=-+-+[cos (cos )]033ππ=----=。

【解法二】应用定积分换元法令3x u π+=，则d x d u =，当x 从3π单调变化到π时，u 从23π单调变化到43π，于是有3s i n ()3x d x πππ+⎰4323s i n udu ππ=⎰4323c o s u ππ=-42[coscos ]33ππ=-- [cos(cos )]033ππ=----=。

⑵132(115)dxx -+⎰；【解法一】应用牛顿-莱布尼兹公式132(115)dx x -+⎰1321(115)(115)5x d x --=++⎰21211(115)52x --=⋅+-22111[]10(1151)(1152)=--+⨯-⨯211(1)1016=--51512=。

【解法二】应用定积分换元法令115x u +=，则15dx du =，当x 从2-单调变化到1时，u 从1单调变化到16，于是有132(115)dx x -+⎰163115u du -=⎰21611152u -=⋅-211(1)1016=--51512=。

⑶32sin cos d πϕϕϕ⎰；【解法一】应用牛顿-莱布尼兹公式320sin cos d πϕϕϕ⎰32cos cos d πϕϕ=-⎰4201cos 4πϕ=-441[cos cos 0]42π=--1[01]4=--14=。

【解法二】应用定积分换元法令cos u ϕ=，则sin d du ϕϕ-=，当ϕ从0单调变化到2π时，u 从1单调变化到0，于是有320sin cos d πϕϕϕ⎰031u du =-⎰130u du =⎰4114u =14=。

定积分换元法和分部积分法

定积分换元法和分部积分法

x
f (t)dt 是奇函数。
0
证明：令
F(x)
x f (t)dt,则F（ x）
x
f (t)dt
0
0
对
F（ x）
x
f (t)dt,
设t=-u有
0
F（ x）
x
x
f (u)(du) f (u)du
0
0
即
F（ x）
x 0
f (u)du
F ( x), F(x),
若f (u) f (u) 若f (u) f (u)
0 f (sin x)dx 0 xf (sin x)dx,
xf (sin x)dx
f (sin x)dx.
0
20
0
1
x
sin x cos2
x
dx
2
0
1
sin x cos2
x
dx
2
0
1
1 cos2
x
d
(cos
x)
arctan(cos
2
x )0
( ) 2 . 2 44 4
sin3 x sin5 xdx
cos
x
sin
x
3
2
dx
0
0
3
2 cos xsin x2 dx
0
cos
xsin
x
3
2
dx
3
2 sin x2 d sin x
0
2
sin
x
3
2
d
sin
x
2
sin
5
x 2
2
2
2
sin
x
5

5.3 定积分的换元法和分部积分法

5.3 定积分的换元法和分部积分法

−a
0
0
a
= ∫ 0 [ f (x ) + f (− x) ]d x
a
a
即
∫ ∫ f ( x)d x = [ f ( x) + f (− x) ] d x
−a
0
a
a
∫ ∫ 即
f (x)d x = [ f (x) + f (−x) ] d x
−a
0
（1）若 f (x) 为偶函数，即 f ( x ) = f (− x )
π
原式 =
t 2
+
ln
|
sin
t
+
cos
t
|
2 0
=π
4
例6：证明
（1）若 f (x) 在 [ - a , a ] 上连续且为偶函数，
a
a
则 ∫ − a f (x)d x = 2∫ 0 f (x)d x
（2）若 f (x) 在 [ - a , a ] 上连续且为奇函数，
a
则 ∫ −a f (x)d x = 0
1 −1
f (u) d u
∫ ∫ ∫ =
1
f (x)d x =
0 (1 + x2 ) d x +
1 e−x d x
−1
−1
0
=
[
x
+
1 3
x
3
]0−1
+
[−e − x ]10
= 7− 1 3e
二、 定积分的分部积分法
设 u = u (x) , v = v(x) 在区间 [ a , b ] 上有连续导
π 2
−
t
dt
π

第三节定积分换元法和分部积分法 (2)共72页

第三节定积分换元法和分部积分法 (2)共72页

2sin n1xd (coxs) 0
sn i 1 x n cx o 2 s 2 (n 1 )sn i 2 x n c2 o x d xs 00
及 f(( t)) ( t) d t F (() ) F (())
F (b)F (a) 从而(1)式成立.
例2. 求a a2x2dx 0
x a
解: 令 x = asint.
当 0xa时 , 0t2 0
x = asint
t
2
且 x 0 t 0 ,
xa t2,
a 2 x 2 a1 s2 it n a ctos
T
T
0 f(x)d xa f(x)d x
故等式成立.
例6. 设 f(x) C (0 [,1 ])则 ,
2f(sxi)d nx2f(cxo )dxs
0
0
证: 作变x换 2t,则
2f(sx i)d nx0f(cto ) (sdt)
2
f (coxs)dx
0
2
0
特别地有
2sin nxdx2conxsdx
证明: (1)式右、左均代表一个数, 我们验证这两个 数相等.
由i)知f (x)在[a, b]上有原函数.设为F(x), 又由
复合函数求导法则.和 ii) 知F((t))是 f ((t))'(t)在 [, ]上的一个原函数.
由Newton-Leibniz公式有
b
af(x)dxF(b)F(a)
一、换元法
例1. 求 2 xex2dx 0
解: Newton-Leibniz公式, 若F' (x) = f (x), 则
a bf(x )d x F (b ) F (a ) F (x )b a

定积分计算例题

定积分计算例题

定积分是微积分的一个重要概念，它是对函数在一个区间上的积累结果的度量。

定积分的计算方法主要有直接法、换元法和分部积分法等。

下面通过几个例题来详细介绍定积分的计算方法。

例1：计算定积分∫(0,2) x^2 dx。

解：根据定积分的定义，我们可以将这个定积分表示为一个求和的形式：∫(0,2) x^2 dx = 1/3 * (x^3) | (0,2) = 8/3所以，定积分∫(0,2) x^2 dx的值为8/3。

例2：计算定积分∫(0,π/2) sin(x) dx。

解：这是一个典型的利用换元法求解的定积分问题。

我们可以令u = sin(x)，则du = cos(x) dx。

因此，原定积分可以转化为：∫(0,π/2) sin(x) dx = ∫(0,π/2) u du = u | (0,π/2) = sin(π/2) - sin(0) = 1所以，定积分∫(0,π/2) sin(x) dx的值为1。

例3：计算定积分∫(0,1) (e^x - x^2) dx。

解：这是一个典型的利用分部积分法求解的定积分问题。

我们可以令u = e^x，则du = e^x dx；v = x^2，则dv = 2x dx。

因此，原定积分可以转化为：∫(0,1) (e^x - x^2) dx = ∫(0,1) u dv -∫(0,1) v du = u*v | (0,1) - [uv] | (0,1) = e^1 - 1 - [e^x*x^2] | (0,1) = e^1 - 1 - (e^1 - 1) = e^1 - e^1 + 1 - 1 = 0所以，定积分∫(0,1) (e^x - x^2) dx的值为0。

通过以上三个例题，我们可以看到定积分的计算方法主要包括直接法、换元法和分部积分法等。

在实际应用中，我们需要根据具体的问题选择合适的计算方法。

同时，我们还需要注意在计算过程中保持变量的一致性，避免出现符号错误。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1．计算下列定积分： ⑴3sin()3x dx πππ+⎰；【解法一】应用牛顿-莱布尼兹公式3sin()3x dx πππ+⎰3sin()()33x d x ππππ=++⎰3cos()3x πππ=-+[cos()cos()]333ππππ=-+-+[cos (cos )]033ππ=----=。

【解法二】应用定积分换元法令3x u π+=，则dx du =，当x 从3π单调变化到π时，u 从23π单调变化到43π，于是有3sin()3x dx πππ+⎰4323sin udu ππ=⎰4323cos u ππ=-42[coscos ]33ππ=-- [cos(cos )]033ππ=----=。

⑵132(115)dxx -+⎰；【解法一】应用牛顿-莱布尼兹公式132(115)dx x -+⎰1321(115)(115)5x d x --=++⎰21211(115)52x --=⋅+-22111[]10(1151)(1152)=--+⨯-⨯211(1)1016=--51512=。

【解法二】应用定积分换元法令115x u +=，则15dx du =，当x 从2-单调变化到1时，u 从1单调变化到16，于是有132(115)dx x -+⎰163115u du -=⎰21611152u -=⋅-211(1)1016=--51512=。

⑶32sin cos d πϕϕϕ⎰；【解法一】应用牛顿-莱布尼兹公式320sin cos d πϕϕϕ⎰32cos cos d πϕϕ=-⎰4201cos 4πϕ=-441[cos cos 0]42π=--1[01]4=--14=。

【解法二】应用定积分换元法令cos u ϕ=，则sin d du ϕϕ-=，当ϕ从0单调变化到2π时，u 从1单调变化到0，于是有320sin cos d πϕϕϕ⎰31u du =-⎰130u du =⎰4114u =14=。

⑷30(1sin )d πθθ-⎰；【解】被积式为3(1sin )d θθ-，不属于三角函数的基本可积形式，须进行变换。

由于1是独立的，易于分离出去独立积分，于是问题成为对3sin d θθ的积分，这是正、余弦的奇数次幂的积分，其一般方法是应用第一换元法，先分出一次式以便作凑微分：sin cos d d θθθ=-，余下的22sin 1cos θθ=-，这样得到的2(1cos )cos d θθ--便为变量代换做好了准备。

具体的变换方式有如下两种： 【解法一】应用牛顿-莱布尼兹公式30(1sin )d πθθ-⎰201sin sin d d ππθθθθ=-⎰⎰20(1cos )cos d ππθθθ=+-⎰301(cos cos )3ππθθ=+-331(cos cos0)(cos cos 0)3πππ=+---1(11)(11)3π=+-----43π=-。

【解法二】应用定积分换元法令cos u ϕ=，则sin d du ϕϕ-=，当ϕ从0单调变化到π时，u 从1单调变化到1-，于是有30(1sin )d πθθ-⎰201sin sin d d ππθθθθ=-⎰⎰20(1cos )cos d ππθθθ=+-⎰121(1)u du π-=+-⎰3111()3u u π-=+-1(11)(11)3π=+-----43π=-。

⑸226cos udu ππ⎰；【解】这是正、余弦的偶次幂，其一般积分方法为，利用三角函数的半角公式：21cos cos 22u u +=，将平方部份降次成为一次的余弦三角函数：21cos 2cos 2u u +=，使之可以换元成为基本可积形式： 【解法一】应用牛顿-莱布尼兹公式226cos udu ππ⎰261cos 22u du ππ+=⎰226611(cos 22)22du ud u ππππ=+⎰⎰ 226611(sin 2)22u u ππππ=+11[()(sin sin )]22623ππππ=-+- 13()234π=-。

【解法二】应用定积分换元法令2u x =，则12du dx =，当u 从6π单调变化到2π时，x 从3π单调变化到π，于是有 226cos udu ππ⎰261cos 22u du ππ+=⎰226611(cos 22)22du ud u ππππ=+⎰⎰23611(cos )22u xdx ππππ=+⎰311[()sin ]2262x ππππ=-+ 11[(sin sin )]2323πππ=+-13()234π=-。

⑹2202x dx -⎰；【解】被积函数中含根号，且根指数及根号内多项式的次数都是2，应该应用第二类换元法中的三角变换法：为使根号内的变量在后的平方差转换成完全平方，应令2sin x u =，当x 从0单调变化到2时，u 从0单调变化到2π，且22222sin 2cos x u u -=-=，2cos dx udu =，使得222x dx -⎰202cos 2cos u udu π=⋅⎰21cos 222udu π+=⎰220cos 2du udu ππ=+⎰⎰2201cos 222uud u ππ=+⎰ 2201sin 22uu ππ=+1(sin 0)22ππ=+-2π=。

⑺211221x dx x -⎰； 【解】被积函数中含根号，且根指数及根号内多项式的次数都是2，应该应用第二类换元法中的三角变换法：为使根号内的变量在后的平方差转换成完全平方，应令sin x u =，当x 从12单调变化到1时，u 从4π单调变化到2π，且2222211sin cos sin sin x u u x u u --==，cos dx udu =，使得 211221x dx x -⎰224cos cos sin u udu u ππ=⋅⎰224cot udu ππ=⎰224(csc 1)u du ππ=-⎰ 24(cot )u u ππ=--[(cotcot )()]2424ππππ=--+-14π=-。

⑻2220ax a x dx -⎰（0a >）；【解】被积函数中含根号，且根指数及根号内多项式的次数都是2，应该应用第二类换元法中的三角变换法：为使根号内的变量在后的平方差转换成完全平方，应令sin x a u =，当x 从0单调变化到a 时，u 从0单调变化到2π，且22222222sin sin sin cos x a x a u a u u a u -=-=⋅，cos dx a udu =，使得222axa x dx -⎰2220sin cos cos a u a u a udu π=⋅⋅⎰422sin 24audu π=⎰4201cos 442a u du π+=⎰421(sin 4)84a u u π=+41[(sin 20)]824a ππ=+-4116a π=。

⑼32211dx xx+⎰；【解】被积函数中含根号，且根指数及根号内多项式的次数都是2，应该应用第二类换元法中的三角变换法：为使根号内的变量在后的平方和转换成完全平方，应令tan x u =，当x 从1单调变化到3时，u 从4π单调变化到3π，且 2222222sec sec tan sec 1tan 1tan dx uduuduu u x x u u ==++2cos sin u du u=21sin sin d u u = 使得32211dx x x +⎰3241sin sin d u uππ=⎰ 这时，再令sin u t =，当u 从4π单调变化到3π时，t 从22单调变化到32， 又得3241sin sin d u u ππ⎰322221dt t =⎰32221t =-22()32=--223=-。

⑽1202x x dx -⎰；【解】被积函数中含根号，且根指数及根号内多项式的次数都是2，应该应用第二类换元法中的三角变换法。

由于根号内的二次多项式并非为三角变换中的平方和或差的标准形式，需要先将其转化为标准形：22221(12)1(1)x x x x x -=--+=--，现在，根号内的二次多项式成为了变量在后的平方差的形式了，因此可令1sin x u -=，当x 从0单调变化到1时，1x -从1-单调变化到0，从而u 对应从2π-单调变化到0， 而且22221sin cos cos x x u u u -=-==，cos dx udu =，于是122x x dx -⎰2cos cos u udu π-=⋅⎰021cos 22u du π-+=⎰0211(sin 2)22u u π-=+11{[0()][sin 0sin()]}222ππ=--+--4π=。

⑾411dxx+⎰；【解】被积函数中含根号，可见根指数与根号内多项式的次数不相等，应该应用第二类换元法中的直接变换法：【解法一】令x u =，当x 从1单调变化到4时，u 从1单调变化到2，且由此得2x u =，2dx udu =，1111ux =++，于是411dx x+⎰2121udu u =+⎰2112(1)1du u =-+⎰212(ln 1)u u =-+ 2[(21)(ln3ln 2)]=---32(1ln )2=-22(1ln )3=+。

【解法二】为便于积分，可使变换后的分母成为简单变量，即令1x u +=，当x 从1单调变化到4时，u 从2单调变化到3，且由此得2(1)x u =-，2(1)dx u du =-，111ux =+，于是411dx x+⎰322(1)u du u -=⎰3212(1)du u =-⎰322(ln )u u =- 2[(32)(ln3ln 2)]=---32(1ln )2=-。

⑿13411dxx --⎰；【解】被积函数中含根号，可见根指数与根号内多项式的次数不相等，应该应用第二类换元法中的直接变换法：【解法一】令1x u -=，当x 从34单调变化到1时，u 从12单调变化到0，且由此得21x u =-，2dx udu =-，11111u x =---，于是13411dxx --⎰01221u du u -=-⎰12012(1)1du u =+-⎰1202(ln 1)u u =+-112(ln ln1)22=+-12ln 2=-。

【解法二】为便于积分，可使变换后的分母成为简单变量，即令11x u --=，当x 从34单调变化到1时，u 从12-单调变化到1-，且由此得21(1)x u =-+，2(1)dx u du =-+，1111ux =--，于是13411dxx --⎰1122(1)u du u ---+=⎰12112(1)du u --=+⎰1212(ln )u u --=+112[()(1)ln ln 1)]22=---+---12ln 2=-。