【人教版】八年级下册导学案反比例函数图像与性质导学案

学习内容：5.2反比例函数的图像与性质11、学习目标：进一步熟悉作函数图象的主要步骤，会作反比例函数的图象；.体会函数的三种表示方法的相互转换，对函数进行认识上的整合。

2、学习重点： 画反比例函数图象并认识图象的特点3、学习难点： 画反比例函数图象并认识图象的特点，理解反比例函数的有关性质一、预习导学1、画函数图像的具体过程是_________,_________,_____________.2、一次函数y=kx=b(k ≠0)，的图像是一条_______,当k>0时，y 随x 增大而________;当k<0时y 随x 增大而_________;正比例函数y=kx （k ≠0）的图像一定经过__________.3.任意写一个在第二象限的点的坐标：_________.4.直线y=-x+3经过第___________象限.5.已知矩形的面积为6，则它的长y 与宽x 之间的函数关系式为_____________,y 是x 的__________函数.6.若函数y=2x m+1是反比例函数，则m=________.7.反比例函数 4y x=经过点（1，__)8、反比例函数的一般表达式为y=_____________(其中__________) 二、自学导学自学教材p147－p149完成下列内容： 反比例函数(0)k y k x=≠的图像是_________,当k>0时，图像位于_________ 象限，当k<0时图像位于________像限。

三、自学检测 1.画出函数 4y x = 的图象。

（1）．列表：3、3、当你看到下面的图象时,你能从中知道些什么?3.若y=（a+2）x a+2a-1为反比例函数关系式，则a= 。

4.下列的数表中分别给出了变量y 与x 之间的对应关系，其中是反比例函数关系的（ ）222,??y y y xxx--===2、下图给出了反比例函数和的图象你知道哪一个是的图象吗为什么5、设面积为20cm 2的平行四边形的一边长为a （cm ）这条边上的高为h （cm ）。

第十七章反比例函数课题17.1.1 反比例函数的意义课时：一课时【学习目标】1.理解并掌握反比例函数的概念。

2.会判断一个给定函数是否为反比例函数。

3.会根据已知条件用待定系数法求反比例函数的解析式。

【重点难点】重点：理解反比例函数的意义，确定反比例函数的表达式。

难点：反比例函数的意义。

【导学指导】复习旧知:1.什么是常量？什么是变量？函数是如何定义的？2.我们学过哪几种函数？每一种函数形式怎样？3.写出下列问题中的函数关系式并说明是什么函数.（1）梯形的上底长是2，下底长是4，一腰长是6，则梯形的周长y与另一腰长x之间的函数关系式。

（2）某种文具单价为3元，当购买m个这种文具时，共花了y元，则y与m的关系式。

学习新知：阅读教材P39－P40相关内容，思考，讨论，合作交流完成下列问题。

1.什么是反比例函数？反比例函数的自变量可以取一切实数吗？为什么？2.仔细观察反比例函数的解析式y=k/x,我们还可以把它写成什么形式？3.回忆我们学过的一次函数和正比例函数，我们是用什么方法求它们的解析式的？以此类推，我们也可以采用同样的方法来求反比例函数的解析式。

【课堂练习】1.下列等式中y是x的反比例函数的是（）①y=4x②y/x=3 ③y=6x－1 ④xy=12 ⑤y=5/x+2⑥y=x/2 ⑦y=－√2/x⑧y=－3/2x2.已知y是x的反比例函数，当x=3时，y=7,(1)写出y与x的函数关系式；（2）当x=7时，y等于多少？【要点归纳】通过今天的学习，你有哪些收获？与同伴交流一下。

【拓展训练】1.函数y=(m－4)x3－|m|是反比例函数，则m的值是多少？2.若反比例函数y=k/x与一次函数y=2x－4的图象都过点A（m,2）(1)求A点的坐标；（2）求反比例函数的解析式。

课题：17.1.2 反比例函数的图象和性质课时：二课时第一课时反比例函数的图象和性质的认识【学习目标】1.体会并了解反比例函数图象的意义。

2.定义及性质：4.总结
学
生
分
析
本堂课立足于学生的“学”，要求学生多动手，多观察，从而可以帮助学生形成分析、对比、归纳的思想方法。在对比和讨论中让学生在“做中学”，提高学生利用已学知识去主动获取新知识的能力。因此在课堂上要采用积极引导学生主动参与，合作交流的方法组织教学，使学生真正成为教学的主体，体会参与的乐趣，成功的喜悦，感知数学的奇妙。
设
计
理
念
创设情境、领悟新知——自主探究、内化新知——拓展应用、升华新知——反馈评价、巩固新知
教
学
目
标
1.进一步熟悉作函数图象的主要步骤，会作反比例函数的图象.
2.体会函数的三种表示方法的互相转换.对函数进行认识上的整合.
重
点
、
难
点
1、画反比例函数的图象；并从函数图象中获取信息。
2、探索并研究反比例函数的主要性质.
5.2反比例授课
年级
九年级
学
科
数学
课题
反比例函数
任课
教师
课型
问题发现课
课时
1
授课时间
教
材
分
析
反比例函数的图象与性质是对正比例函数图象与性质的复习和对比，也是以后学习二次函数的基础。本课时的学习是学生对函数的图象与性质一个再知的过程，由于初三学生是首次接触双曲线这种函数图象，所以教学时应注意引导学生抓住反比例函数图象的特征，让学生对反比例函数有一个形象和直观的认识。
练习巩固，
提升能力
15分钟
完成“问题训练----评价单”
教师巡视指导，个别问题个别处理
学生自主完成，疑难问题合作解决
总结归纳
提升意义

反比例函数的图象和性质（一）学习目标会画反比例函数的图象，并知道该图象与正比例函数、一次函数图象的区别，能从反比例函数的图象上分析出简单的性质．初步掌握反比例函数的图象和性质．． 自学探究：例1．（补充）已知反比例函数52)1(--=m x m y 的图象在第二、四象限，求m 值，并指出在每个象限内y 随x 的变化情况？ 1．反比例函数xky =(k 为常数，k ≠0)的图象是______；当k ＞0时，双曲线的两支分别位于______象限，在每个象限内y 值随x 值的增大而______；当k ＜0时，双曲线的两支分别位于______象限，在每个象限内y 值随x 值的增大而______．2．如果函数y ＝2x k ＋1的图象是双曲线，那么k ＝______．3．已知正比例函数y ＝kx ，y 随x 的增大而减小，那么反比例函数xky =，当x ＜0时，y 随x 的增大而______．4．如果点(2，－5)在双曲线xky =上，那么该双曲线在第______象限． 5．如果反比例函数xk y 3-=的图象位于第二、四象限内，那么满足条件的正整数k 的值是____________． 6.反比例函数xy 1-=的图象大致是图中的( )．7．下列函数中，当x ＞0时，y 随x 的增大而减小的是( )．(A)y ＝x(B)xy 1=(C)xy 1-= (D)y ＝2x自我检测 班级： 姓名：1.反比例函数y=x k的图象位于第二、四象限，则k 的取值范围是（ ）.A. k ＜1B. k ＞1C. k ＝1D. 0＜k ＜12. 反比例函数y=x k中，如果k ＞0，x ＜0，那么它的图象在（ ）. A. 第一、三象限 B. 第二、四象限 C. 第三象限 D.第四象限 3．下列反比例函数图象一定在第一、三象限的是( )．(A)x my =(B)xm y 1+=(C)xm y 12+=(D)xmy -=4．反比例函数y ＝221)(2--mx m ，当x ＞0时，y 随x 的增大而增大，则m 的值是( )．(A)±1(B)小于21的实数 (C)－1 (D)17．作出反比例函数xy 12=的图象，并根据图象解答下列问题： (1)当x ＝4时，求y 的值； (2)当y ＝－2时，求x 的值； (3)当y ＞2时，求x 的范围．五、小结与反思：。

y = x
1 反比例函数的图像与性质（一）
学习目标：
1、进一步熟悉作函数图象的主要步骤，会作反比例函数的图象；
2、观察反比例函数图象的特征从中得到反比例函数的简单性质
3、在自主探究反比例函数性质的过程中，感知反比例函数图象的对称性 过程：
一、复习回顾，引入新知
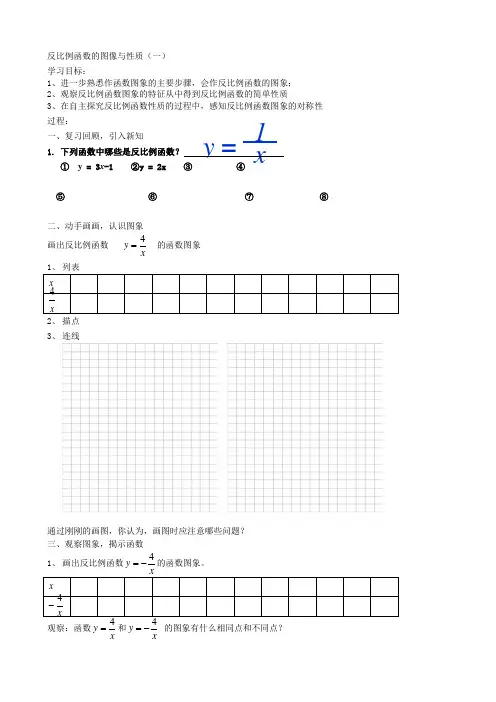
1. 下列函数中哪些是反比例函数？ ① y = 3x -1 ②y = 2x ③ ④
⑤ ⑥ ⑦ ⑧
二、动手画画，认识图象 画出反比例函数 x
y 4
= 的函数图象
2、 描点
3、 连线
通过刚刚的画图，你认为，画图时应注意哪些问题？ 三、观察图象，揭示函数 1、 画出反比例函数
y 4
-
=的函数图象。

观察：函数x
y =
和x y -= 的图象有什么相同点和不同点？
四、运用新知，巧妙解答
3、反比例函数 经过点（1， ）。

选作：5、若点 在函数 （x ＜0）的图象上，且 ，则它的图象大致是（ ）(2008年江西中考题）
五、自我反思，自我收获 1、 知识收获 2、合作收获 六、作业 必做： 选作：
自留作业：根据今天画 和 两个 函数图象，请你继续探索，反比例函数还存在什么性质？
),(00y x x
k y =200-=y x。

反比例函数的图像和性质（1）导学案学习目标1．会画反比例函数图象，理解反比例函数的图象和性质．2．感悟“数形结合”、“变化与对应”和“转化”的数学思想，并能应用数形结合和转化思想根据反比例函数的图象探究其性质．学习重点：1、反比函数的图像画法2、反比例函数的性质。

学习难学习难点：反比例函数的性质。

一、知识链接：（忆一忆）（注意：这里第1、2题要学生在上课前写在黑板上，可以多写几组，上课时，老师要稍微点一下。

为下面探究反比例函数的性质做一个铺垫。

3、4题问一下就可以了。

）1、函数做图的步骤是___________、_______________、____________。

2、正比例函数的性质填写下表：3、正比例函数的图像和性质是怎么得到的？是如何研究的？（经过哪几个步骤）4、反比例函数的表达式 ___________________________解析式中自变量x的取值能为0吗？为什么______________________、二、合作探究、展示交流1、做一做（展示）问题：反比例函数的图像是什么样的？画出下列函数图像①y=10/x y=8/x y=6/x（注意每两个小组做一个）做图应该注意的几点：（注意这里是学生在做图时思考的问题，教师在讲解时也要让学生进行口答）（1）列表时取值应注意什么？x的取值能为零吗？为什么？（2）连线时应该注意什么？（3）反比例函数图像还是直线吗？是什么？（4）图像和坐标轴有交点吗？为什么？（这里需要小组合作探究一下，从图像中和解析式中一起来考虑）2、议一议（这是小组合作的部分，要求小组成员合作完成）问题一：（1）观察前三个函数的解析式有什么共同点：（2）观察前三个函数图像有什么共同点：有哪些特征？你能填写下表吗？3）当取不同大于0的值时，上述结论是否适用于所有的反比例函数？（注意：这里需要教师用几何画板演示，还有要学生从解析式来分析所有的函数都符合这一规律）问题二：做出下列反比例函数的图像：④y=－6/x ⑤y=－8/x ⑥y=－10/x （注意每两个小组做一个）（4）观察后三个函数解析式有什么共同点：（5）观察后三个函数的图像有什么共同点：你能填写下表吗？（6）当取不同小于0的值时，上述结论是否适用于所有的反比例函数？问题三：（7）前三个函数解析式和后三个函数解析式有什么不同？（k的取值范围不同）前三个函数图象和后三个函数图象有什么不同？由什么决定的?（8）你能总结出反比例函数图像的性质吗？在新课改的形式下，如何激发教师的教研热情，提升教师的教研能力和学校整体的教研实效，是摆在每一个学校面前的一项重要的“校本工程”。

2019-2020学年八年级数学下册《反比例函数的图像和性质》导学案2新人教版
课题
１７.１.２反比例函数的图象和性质（１）
设计教师
学生活动
预习笔记（关键点、知识点、切入点及纠错）
预
习
目
标
1、会用描点的方法画反比例函数图象.
2、理解反比例函数的性质.
活动 三：
对k的值进行分类讨论，自选k的值，画函数y=k/x的图象.
达标测评
１.反比例函数y=５/x的图象大致是（）
AB CD
２.函数y=－２/x的图象 在第________象限,在每一象限内，y随x的增大 而_________.３.函数y=40/x的图象在第________象限,在 每一象限内，y随x的增大而_________.４.函数y=－π/x,当x>0时,图象在第____象限, y随x的增大而_________.５.已知反比例函数y=(２-k)/x,若函数的图象位于第一、三象限，则k_____________;若在每一象限内，y随x增大而增大，则k_____________.
1、图象在第一、第三象限的函数与图像在第二、第四象限的函数的k值有何区别?
2、在每 一个象限内，y随x的变化如何变化？
活动四
（一）强化基础
（三）实际应用
3.函数 y=10/x的图象在第________象限,在每一象限内，y随 x的增大而______ ___.4.函数y=-20/x的图象在第________象限,在每一象限内，y随x的增大而_________.5.函数y=π/x,当x>0时,图象在第____象限, y随x的增大而_________.6.已知反比例函数y=(4-k)/x,若函数的图象位于第一、三象限，则k_____________;若在每一象限内，y随x增大而增 大，则k_____________.

17.1.2 反比例函数的图像和性质（2）<目标导学> 1.会根据反比例函数图象的某些特征，分析并掌握反比例函数的性质．2.能运用反比例函数图象与对应的函数关系解决有关问题．3.根据所给反比例函数与一次函数的图象解决一些简单的综合问题．【重点难点预设】重点：用反比例函数的图象和性质解决数学中的简单问题。

难点：数形结合思想在解题中的应用。

正确理解反比例函数的意义【学习过程】温故知新1.作反比例函数图象的基本步骤是⑴；⑵；⑶。

2．反比例函数的图象是由组成的，通常称为，当k<0时位于；当k>0时位于。

3.反比例函数的图象，当k>0时,在每一个象限内，y的值x随的增大而；当k<0时，在每一个象限内，y的值随x的增大而。

4.反比例函数的图象上任取一点，过这一点分别作x轴、y轴的平行线，与坐标轴围成的矩形面积是。

5.试填写下表，并说说正比函数与反比例函数的区别.正比例函数反比例函数函数关系式图像性质K>0 K<0一、自主学习（预习独学）阅读课本第44页至45页的部分二、合作探究（对学研讨）认真阅读，挑战记忆力1、老师在黑板上写了这样一道题：“已知点（2，5）在反比例函数y=的图象上，•试判断点（-5，-2）是否也在此图象上．”题中的“？•”是被一个同学不小心擦掉的一个数字，请你分析一下“？”代表什么数，并解答此题目．2、模仿【例3】做下题：已知反比例函数的图象经过点A（3，－4）。

（1）这个函数的图象分布在哪些象限？在图象的每一支上，y随x的增大如何变化？（2）B（－3，4）点、C（－2，6）点和点D（3，4）是否在这个函数的图象上？3、模仿【例4】做下题：如下图是反比例函数的图象的一支，根据图象回答下列问题：（1）图象的另一支在哪个象限？常数n的取值范围是什么？（2）在图象上任取一点A（a，b）和B（a＇,b＇），如果a< a＇，那么b和b＇有怎样的大小关系？第四步：达标测评（测评反馈）1.函数的图像在第二、第四象限，则m的取值范围是 .2.函数与在同一坐标系中的图像是（）3.问题：如下图，点A、B在反比例函数的图象上，且点A、B的横坐标分别为a，2a（a>0），AC⊥x轴，垂足为点C，且△AOC的面积为2。

§反比率函数y k0 ）的图象与性质（ kx【学习目标】1. 学会用描点法作反比率函数的图象，理解并掌握反比率函数的性质并能灵巧运用.2. 逐渐提升从函数图象中获守信息的能力，研究并掌握反比率函数的主要性质.3. 经过对图象性质的研究，训练学生的研究能力和语言组织能力.【要点】反比率函数图象的画法及研究反比率函数的性质.【难点】反比率函数是光滑双曲线的理解以及经过察看、剖析，概括出反比率函数的性质并能灵巧运用【预学导航】一、自主学习1、研究：在以下图的方格坐标纸内，怎样画反比率函数y6 的图象？①列表：因为自变量 x 的取值范围是xx 取一些正数值和负数值，，先让自变量计算出相应的函数值y ，列成以下表格：x...-6-5-4-3-2 -1 1 234 566...yx②描点：成立平面直角坐标系，以自变量值为横坐标，相应的函数值为纵坐标，描出这些点.③连线：把 y 轴右侧各点和左侧各点，分别用一条圆滑曲线按序连结起来..... ...x ... -5 -4 -3 -2 -1 1 2 3 4 5 ...y 3... ...x2 、试一试：在左边方格坐标纸内，3画出反比率函数y的图象：x3、察看经过画6与 y3y 的图象，回答以下问题：x x①每个函数的图象分别位于哪些象限？②在每个象限内，函数值y 随自变量x的变化怎样变化？【合作研究】已知点 A x1 , y1 ， B x2 , y2 ， C x3 , y3在反比率函数y 3x1 0 x2 x3，的图象上，且知足x试比较 y1， y2， y3的大小.【当堂检测】1.以下函数图象中，是反比率函数的图象的是（）2. 已知反比率函数y k0 ，在每个象限内，y 随x增大而. （ k 为常数， k 0）的图象以下图，则 k1 x3. 反比率函数y 的图象在第象限，x象限， y 随x增大而当 x 0 时，图象在第；当 x 0 时，图象在第象限， y 随x增大而.4. 若双曲线 y3m 1m 的取值范围是.在每个象限内 y 随x增大而减小，则a2x5. 双曲线 y1经过第象限，在每个象限内，y 随x增大而. x6. 已知点 A 2, y1 ， B 1, y2 在反比率函数 y k0 ）的图象上，则y1 y2. （ kx【讲堂小结】1. 谈谈本节课你的收获，领会，迷惑.2.你在本节课的学习过程中有何想法？（重视知识，思想方法上）3.本节课你能提出什么问题？【课后反省】。

二合作探究 1. 重申学习目标 2. 检查预习情况 3. 合作交流 1、画出反比例函数 y =
x … … -6 -5
6 6 与 y = − 的图象． x x
-4 -3 -2 -1 1 2 3 4 5 6 … …
6 x 6 y=− x y=
…
…
6 5 4 3
2
y
6 5 4 3
2
y
1
1
0
- -
-
-
-
-
1 2
板书设计： 17．1．2 反比例函数的图象和性质（1） 1、反比例函数的图像和性质 4、小结 2、课堂练习 3、课堂检测
导后记：
4．已知反比例函数 y = (a − 2) x
a 2 −6
，当 x > 0 时，y 随 x 的增大而增大，求函数
关系式
5．已知反比例函数 y = (m − 1) x m −3 的图象在第二、四象限，求 m 值，并指出 在每个象限内 y 随 x 的变化情况？
2
四、课堂小结 谈谈你今天的收获？ 五、作业 1、书 46 页 3、4 题 2、预习下一课
一）
1、能描点画出反比例函数的图象. 2、通过反比例函数的图象的分析，探索并掌握反比例函数的图象 的性质。 探索并掌握反比例函数的主要性质。 合作交流，讲练结合 教具
课前准备 1．一次函数 y＝kx＋b（k、b 是常数，k≠0）的图象是什么？其性质有哪些？ 正比例函数 y＝kx（k≠0）呢？
2．画函数图象的方法是什么?其一般步骤有哪些哪些？
3 4 5
-1
-2
6 x- -
-
-
-
-
0
1 2
3 4 5
-1

自主学习任务单——11.2 反比例函数的图像与性质（2）一、学习目标1．能根据图像分析和理解反比例函数的性质，感受数形结合的数学思想；2．会用待定系数法求反比例函数表达式，并能运用反比例函数的性质解决问题.二、学习过程（一）温故而知新还记得反比例函数6yx＝、6yx＝－的图像吗？请画出它们的图像.（二）探索发现活动一：想一想观察反比例函数6yx＝、6yx＝－的图像，思考并回答以下问题问题1：每个函数的图像分别在哪几个象限？问题2：在每个象限内，随着x的增大，y是怎样变化的？问题3：反比例函数的图像与x轴有交点吗？与y轴有交点吗？为什么？活动二：议一议反比例函数kyx＝（k为常数，k≠0）的图像是双曲线.问题1：你觉得反比例函数图像的分布与性质和谁有关？问题2：当k＞0时，双曲线的两支分布在象限，在每一个象限内，y随x 的增大而；问题3：当k＜0时，双曲线的两支分布在象限，在每一个象限内，y随x 的增大而.（三）理解运用例1已知反比例函数y ＝k x的图像经过点A （2，－4）． （1）求k 的值；（2）这个函数的图像在哪几个象限？在每个象限内，y 随x 的增大怎样变化？（3）画出函数的图像；（4）点B （12，－16）、C （－3，5）在这个函数的图像上吗？；练习：已知反比例函数的图像经过点41-（，）. （1） 试确定该函数表达式；（2） 若点12y -（，），2(1)y -，在该函数图像上，则1y 2y （用“＞”或“＜”填空）.（四）探索研究 完成课本P130页的“探索”，思考反比例函数的两支图像对称吗？（五）总结反思1．如何用待定系数法求反比例函数表达式？2．当k ＞0时，双曲线的两支分别在哪几个象限，在每一个象限内，y 随x 的变化如何变化；当k ＜0时，双曲线的两支分别在哪几个限，在每一个象限内，y 随x 的变化如何变化？3．反比例函数图像的对称性如何？三、效果检测1．对于函数y ＝6x，下列说法错误的是 ( )A.它的图像分布在第一、三象限B.它图像的两个分支关于原点对称C.当x>0时，y 的值随x 的增大而增大D.当x<0时，y 的值随x 的增大而减小 2.已知点A (1，1y )、B (2，2y )、C （－3，3y ）都在反比例函数y ＝6x 的图像上，则1y 、2y 、3y 的大小关系是 ( ) A ．312y y y << B ．123y y y << C ．213y y y << D ．321y y y << 3．已知反比例函数y ＝26m x-，当m _______时，其图像的两个分支在第二、四象限内；当m _______时，其图像在每个象限内y 随x 的增大而减小．4．已知反比例函数的图像经过点A （ － 6，－3）.（1）确定这个反比例函数的表达式；（2）这个函数的图像在哪几个象限？在每个象限内，y 随x 的增大怎样变化？（3）点B （4，29）、C （2，－5）在这个函数的图像上吗？附件1：教材内容附件2：效果检测答案：1.C 解析：因为k = 6>0，所以图像分布在第一、三象限，在每个象限内y 的值随x 的增大而减小；反比例函数的两支图像关于原点对称.所以该题选C.2.D 解析：因为k = 6 >0，在每个象限内y 的值随x 的增大而减小，且（－3，3y ）在第三象限，所以321y y y << ，该题选D.3.3m <；3m > . 解析：其图像的两个分支在第二、四象限内，所以k =2m －6<0 ，所以 3m <；因为其图像在每个象限内y 随x 的增大而减小，所以k = 2m －6 >0，所以3m >.4.（1） x y 18=解析：解设y ＝k x（k 为常数，k ≠0），把A （ － 6，－3）代入得k =18.（2）因为k = 18>0，所以这个函数的图像在第一、三象限，在每一个象限内，y 随x 的增大而减小. （3）当x = 4时，y =29，所以点B 在函数图像上；当x = 2时，y ≠－5，所以点C 不在函数图像上.。

问题 5：尝试着在平面直角坐标系内画出反比例函数 y 6 的图像，并比较 y 6 与 y 6 的
x
x
x
图像特征 .
【新知归纳】 1.反比例函数 y 2.反比例函数 y 3.反比例函数 y
6 的图像是 ________.
x
6 的图像经过 _______象限，在每个象限内， y 随 x 的增大而 ____. x
自主学习任务单
—— 11.2 反比例函数的图像与性质（ 1） 一、学习目标
1.根据反比例函数的表达式初步描述函数图像的一些特征，能画出反比例函数的图像； 2.能在探索反比例函数图像画法的过程中进一步理解函数的 3 种表达方式； 3.体会类比和数形结合的思想方法 .
二、学习过程
（一）知识回顾 问题：画函数图像的一 般步骤是什么？
问题 4：根据反比例函数 y 6 的图像，你能发现反比例函数的哪些性质？ x
【新知归纳】 1.反比例函数 y 2.反比例函数 y 3.反比例函数 y
6 的图像是 ________. x
6 的图像经过 _______象限，在每个象限内， y 随 x 的增大而 ____.
x
6 图像的两个分支关于 x
对称 .
x
别是垂足， (1)求四边形 PAOB 的面积； (2)P 点向左移动时，四边形 PAOB 的面积如何变化？
[来源 :
* 科 * 网 Z*X*X*K]
(五）反思总结 1.画函数图像采用的方法是什么 ?其步骤有哪些 ?要注意些什么 ? 2.实际问题中画函数图像要注意什么 ?
三、效果检测
k
k
1. 反比例函数 y x 的图像经过点 (- 1,2) ，那么下列各点中不在 y x 图像上的是 (

A、 B、
C、 D、
3.反比例函数的图象上任取一点，过这一点分别作x轴、y轴的平行线，与坐标轴围成的矩形面积是。
第四步ห้องสมุดไป่ตู้达标测评（测评反馈）
1.若反比例函数的图象在第二、第四象限，则直线y=kx－3不经过第象限。
2. 反比例函数y=的图象分布在二、四象限，则k的取值范围是
评价与反思：
教师“复备”栏或学生笔记栏
【学习过程】第一步：学生预习（预习独学）
阅读课本第 41页至43 页的部分，完成以下问题：
⑴ 画函数的图象：⑵ 求上述函数与轴、轴的交点坐标。
思考：1.什么叫做反比例函数？
2.试猜想反比例函数的图象是什么样的？自己尝试作反比例函数图象
第二步：学生合作（对学研讨、群学探究）模仿课【例2】
在下面的平面直角坐标系中，画出反比例函数与的图象.
观察函数和以及和的图象，思考：
1）你能发现它们的共同特征以及不同点吗？2）每个函数的图象分别位于哪几个象限？3）在每一个象限内，y随x的变化如何变化？
归纳：
第三步：学生展示（群学探究与展示）
1.请指出下面的图象中,如下图哪一个是反比例函数的图象 （ ）
2．如右下图，这是下列四个函数中哪一个函数的图象（ ）
17.1.2课题：反比例函数的图象和性质(1)
<目标导学>1.进一步体会作函数图象的主要步骤，会作反比例函数的图象。
2.体会函数三种表示方法的相互转换，对函数进行认识上的整合。
3.探索并掌握反比例函数的性质,体会分类讨论思想、数形结合思想的运用。
【重点难点预设】重点：掌握反比例函数的作图。难点：反比例函数三种表示方法的相互转换。

反比例函数的图象和性质导学案（2）备课人：王伟亚学习目标：1．使学生进一步理解和掌握函数及其图象与性质 2．能理解并运用反比例函数xk y =中K 的几何意义。

3．能综合运用反比例函数的图像和性质。

4．培养学生数形结合的思想。

学习重点：理解并掌握反比例函数的图象和性质，并能利用它们解决关于K 的函数问题 学习难点：学会从图象上分析、解决反比例函数问题。

一、导1．判断下列说法是否正确（1）反比例函数图象的每个分支只能无限接近x 轴和y 轴，但永远也不可能到达x 轴 或y 轴．（ ） （2）在y=3x中，由于3>0，所以y 一定随x 的增大而减小．（ ）（3）已知点A （-3，a ）、B （-2，b ）、C （4，c ）均在y=-2x的图象上，则a<b<c ．（ ）（4）反比例函数图象若过点（a ，b ），则它一定过点（-a ，-b ）．（ ） 2．点（1，3）在反比例函数y=k x(k ≠o)的图象上，则k= ，在图象的每一支上，y 随x •的增大而 ． 3．（1）如图过双曲线xk y =(k ≠o)上任一点p （x 、y ）作x 轴、y轴垂线段PM 、PN 所得矩形PMON的面积S=PM ·___=___·___=|xy| ∵xk y =∴xy=k ∴s=_____，即反比例函数y=kx（k ≠0）中的比例系数的k 的绝对值表示过双曲线上任意一点，作X 轴，Y 轴的垂线所得的__________。

（2）如图过双曲线上一点Q 向X 轴或Y 轴引垂线，则S △AOQ =21______二、学例1．如图，P 为反比例函数xk y =(k ≠o)上的一点，若图中阴影部分矩形的面积是2，求这个反比例函数的解析式。

解：设P 的坐标为（x ，y ），过点P 分别作x 轴和y 轴的垂线段，由题意可知：︱x ︳.︱y ︳=_______,∵P 在第___象限。

∴x___,y_____ ∵x.y=____,∴k=_____∴这个反比例函数的解析式为：_________ 三、练一级变式题：1．在平面直角坐标系内，过反比例函数xk y =（k ＞0）的图象上的一点分别作x 轴、y 轴的垂线段，与x 轴、y 轴所围成的矩形面积是6，则函数解析式为 2．如图，过反比例函数xy 1=（x ＞0）的图象上任意两点A 、B 分别作x 轴的垂线，垂足分别为C 、D ，连接OA 、OB ，设△AOC 和△BOD 的面积分别是S 1、S 2，比较它们的大小，可得（ ） （A ）S 1＞S 2 （B ）S 1＝S 2（C ）S 1＜S 2 （D ）大小关系不能确定 二级变式题：1．如图A 是反比例函数`4x y =图象上一点，AB ⊥y 轴于点B ，则△AOB 面积是（ ）A. 1B. 2C. 3D. 42．如图是三个反比例函数 在x 轴上方的图像， 由此观察得到( )A k1>k2>k3B k3>k2>k1C k2>k1>k3D k3>k1>k23．已知k >0,则函数 y 1=kx+k 与y 2=在同一坐标系中的图象大致是 ( )例2．如图所示，已知直线1y =x+m 与x 轴、y •轴分别交于点A 、B ，与双曲线2y = （k<0）分别交于点C 、D ，且C 点坐标为（-1，2）． （1）分别求直线AB 与双曲线的解析式；（2）求出点D 的坐标(3）利用图象直接写出当x 在什么范围内取何值时，y 1>y 2． 解：（1）∵C （-1，2）在双曲线2y = 上，∴______________________________xk y ,x ky ,x k y 332211===xk x kxk∴K=________∵C （-1，2）在直线1y =x+m 上∴____________________________ ∴m = ______∴直线AB 与双曲线的解析式分别为____________(2) ∵直线1y =x+m 与双曲线2y = （k<0）交于点C 、D ，∴可得方程组： ——————————————解这个方程组得：∴D 点坐标为（-2，1）（3）观察图像可知，当x_____________ 时，y 1>y 2。

反比例函数的图像和性质（1）导学案学习目标1．会画反比例函数图象，理解反比例函数的图象和性质．2．感悟“数形结合”、“变化与对应”和“转化”的数学思想，并能应用数形结合和转化思想根据反比例函数的图象探究其性质．学习重点：1、反比函数的图像画法2、反比例函数的性质。

学习难学习难点：反比例函数的性质。

一、知识链接：（忆一忆）（注意：这里第1、2题要学生在上课前写在黑板上，可以多写几组，上课时，老师要稍微点一下。

为下面探究反比例函数的性质做一个铺垫。

3、4题问一下就可以了。

）1、函数做图的步骤是___________、_______________、____________。

2、正比例函数的性质填写下表：3、正比例函数的图像和性质是怎么得到的？是如何研究的？（经过哪几个步骤）4、反比例函数的表达式 ___________________________解析式中自变量x的取值能为0吗？为什么______________________、二、合作探究、展示交流1、做一做（展示）问题：反比例函数的图像是什么样的？画出下列函数图像①y=10/x y=8/x y=6/x（注意每两个小组做一个）做图应该注意的几点：（注意这里是学生在做图时思考的问题，教师在讲解时也要让学生进行口答）（1）列表时取值应注意什么？x的取值能为零吗？为什么？（2）连线时应该注意什么？（3）反比例函数图像还是直线吗？是什么？（4）图像和坐标轴有交点吗？为什么？（这里需要小组合作探究一下，从图像中和解析式中一起来考虑）2、议一议（这是小组合作的部分，要求小组成员合作完成）问题一：（1）观察前三个函数的解析式有什么共同点：（2）观察前三个函数图像有什么共同点：有哪些特征？你能填写下表吗？3）当取不同大于0的值时，上述结论是否适用于所有的反比例函数？（注意：这里需要教师用几何画板演示，还有要学生从解析式来分析所有的函数都符合这一规律）问题二：做出下列反比例函数的图像：④y=－6/x ⑤y=－8/x ⑥y=－10/x （注意每两个小组做一个）（4）观察后三个函数解析式有什么共同点：（5）观察后三个函数的图像有什么共同点：你能填写下表吗？（6）当取不同小于0的值时，上述结论是否适用于所有的反比例函数？问题三：（7）前三个函数解析式和后三个函数解析式有什么不同？（k的取值范围不同）前三个函数图象和后三个函数图象有什么不同？由什么决定的?（8）你能总结出反比例函数图像的性质吗？。

26．2反比例函数的图象和性质（1）导学案甘肃泾川县罗汉洞中学 刘隆基一、温故知新1．画函数图象的一般步骤是（1） ；（2） ；（3） 。

2．一次函数y ＝kx ＋b （k 、b 是常数，k ≠0）的图象是 ，性质是： 。

3.反比例函数的反比例函数的表达式是 ____________ _______；解析式中自变量x 的取值能为0吗？ 为什么？_______________ _______。

二、新知导学 1.（1）y=x 6（2）y=x8（１、２两个函数同桌两人合作，每人选一个画）（3）y=－x 6（4）y=－x 8（３、４两个函数同桌两人合作，每人选一个画）画图时注意：（1）列表时取值应注意什么？（2）连线时应该注意什么？（３）x 的取值能为零吗？图像和坐标轴有交点吗？为什么？2.合作探究探讨1.观察上面图形想想下列问题：（1）反比例函数x k y 的图象是由 组成的.（通常称为 ） （2）当k =６时，两支曲线分别位于第 象限内，在每一象限内．．．．．．，y 值随 。

（3）当k =-６时，两支曲线分别位于第 象限内，在每一象限内．．．．．．，y 值随 。

（4）y=x 6和y=-x6的图象关于 对称。

归纳：反比例函数（ ）的图像和性质：反比例函数的图像是 ；当k ＞0时，双曲线的两支分别位于___ ___象限，在每个象限内y 值随x 值的增大而______；当k ＜0时，双曲线的两支分别位于__ ____象限，在每个象限内y 值随x 值的增大而______．３．典例分析：例1．已知反比例函数52)1(--=mx m y 的图象在第二、四象限，求m 值，并指出在每个象限内y 随x 的变化情况？对应练习： １．已知反比例函数xk y =的图象如图所示，则k 0， 且在图象的每一支上，y 值随x 的增大而 ．２．反比例函数y=1m x -的图象在第二、四象限，则m 的取值范围是:___．３．反比例函数xy 2-=，当x ＝－2时，y ＝ ；当x ＜－2时；y 的取值范围是；当x ＞－2时；y 的取值范围是 。

17．1．2 反比率函数的图象和性质（1）导教案学习目标： 1．会用描点法画反比率函数的图象2．联合图象剖析并掌握反比率函数的性质学习要点：理解并掌握反比率函数的图象和性质学习难点：正确画出图象，经过察看、剖析，概括出反比率函数的性质学习过程：一、课前准备：1.正比率函数y＝ kx （ k≠0）的图象是什么？其性质有哪些？一次函数呢？2.画函数图象的一般步骤有哪些？应注意什么？二、讲堂学习画出反比率函数6和 y6y的图象 .( 可分组达成 ) x x解 : 列表表示几组x 与y的对应值(填表)x-6-5-4-3-2-11234566yx6yx描点连线 :注意：（1）列表取值时，x≠ 0，因为 x＝0 函数无心义，为了使描出的点拥有代表性，能够“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y 值（2）因为函数图象的特色还不清楚，因此要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精准（ 3）连线时要用光滑的曲线依据自变量从小到大的次序连结，切忌画成折线（ 4） x≠ 0， k≠ 0，因此 y≠ 0，函数图象永久不会与x 轴、 y 轴订交，不过无穷凑近两坐标轴。

思虑反比率函数 y66和 y的图象有什么共同特色？它们有什么关系？概括总结反比x x例函数图像特色和性质反比率函数 yk0 ）图像是_____________（ k 为常数， kx图像性质当 k >0当 k <0注意：描绘函数值的增减状况时，一定指出“在函数图像所在的哪个象限内”三、随堂练习1．点 (1, 6) 在双曲线yk上，则 k=______________.x2．已知反比率函数y6的图象经过点 P( 2, a) ，则 a=__________.x3．函数y ( a2) x a26，当 x 0 时，y随x的增大而增大，则函数关系式为__________4. 做出以下反比率函数的图像：y=－ 8/x y=－10/x117．1．2 反比率函数的图象和性质（2）导教案学习目标：1．联合图象剖析并掌握反比率函数的性质。