全等三角形类型题汇总
- 格式：docx
- 大小：151.86 KB
- 文档页数：15
下载文档原格式
合集下载
全等三角形习题精选(含答案)
全等三角形习题精选(含答案)1.在图中，已知△ABC≌△ADE，BC的延长线过点E，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，求∠DEF的度数。
2.在图中，已知△AOB中，∠B=30°，将△AOB绕点O 顺时针旋转52°，得到△A′OB′，边A′B′与边OB交于点C（A′不在OB上），则∠A′CO的度数为多少？3.在图中，已知△ABC中，∠A=90°，D、E分别是AC、BC上的点，若△AADB≌△EDB≌△EDC，则∠C的度数是多少？4.在图中，把△ABC绕点C顺时针旋转35°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=？5.已知，如图所示，AB=AC，AD⊥BC于D，且AB+AC+BC=50cm，而AB+BD+AD=40cm，则AD的长度是多少？6.在图中，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B、C作过点A的垂线BC、CE，垂足分别为D、E，若BD=3，CE=2，则DE的长度是多少？7.在图中，AD是△XXX的角平分线，DE⊥AB，DF⊥AC，垂足分别是E、F，连接EF，交AD于G，需要证明AD与EF垂直。
8.在图中，△ABC中，AD为∠BAC的角平分线，DE⊥XXX于E，DF⊥AC于F，△ABC的面积是28cm，AB=20cm，AC=8cm，求DE的长度。
9.已知，如图所示：AB=AE，∠B=∠E，∠BAC=∠EAD，∠XXX∠DAF，需要证明AF⊥CD。
10.在图中，已知AD=BD，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点H，需要判断BH是否等于AC，并解释原因。
11.在图中，已知AD为△ABC的高，E为AC上一点，BE交AD于F，且有ABF=AC，FD=CD，需要证明BE⊥AC。
12.在图中，△DAC、△EBC均是等边三角形，AF、BD分别与CD、CE交于点M、N，需要证明：（1）AE=BD（2）CM=CN（3）△CMN为等边三角形（4）MN∥BC。
全等三角形经典50题(含答案)
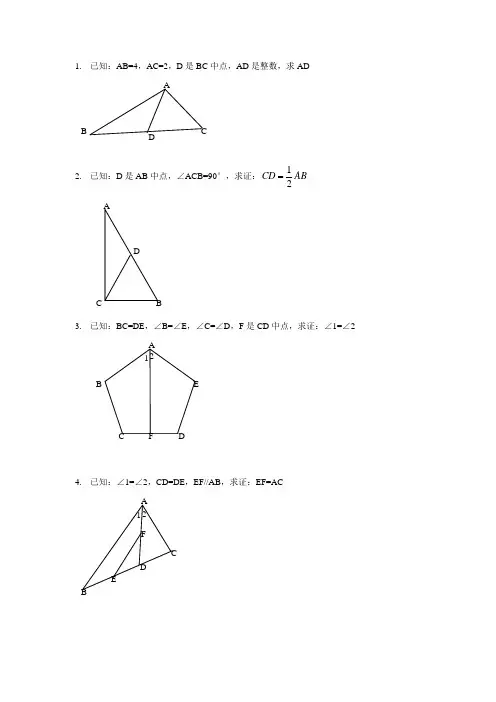
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=ACAD BC BACDF21E5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠ C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD8. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB AD BC A9.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。
∵BC=ED,CF=DF,∠BCF=∠EDF。
∴三角形BCF全等于三角形EDF(边角边)。
∴BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
∴ ∠EBF=∠BEF 。
又∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
10. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CG∠CGD ＝∠EFD又EF ∥AB∴∠EFD ＝∠1∠1=∠2∴∠CGD ＝∠2∴△AGC 为等腰三角形，AC ＝CG又 EF ＝CG∴EF ＝AC11. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CB ACDF21 E证明：延长AB 取点E ，使AE ＝AC ，连接DE∵AD 平分∠BAC∴∠EAD ＝∠CAD∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ）∴∠E ＝∠C∵AC ＝AB+BD∴AE ＝AB+BD∵AE ＝AB+BE∴BD ＝BE∴∠BDE ＝∠E∵∠ABC ＝∠E+∠BDE∴∠ABC ＝2∠E∴∠ABC ＝2∠C12. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC又∵AC ＝AC∴△ADC ≌△AFC （SAS ）CD B A∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
全等三角形经典题型50题(含答案)
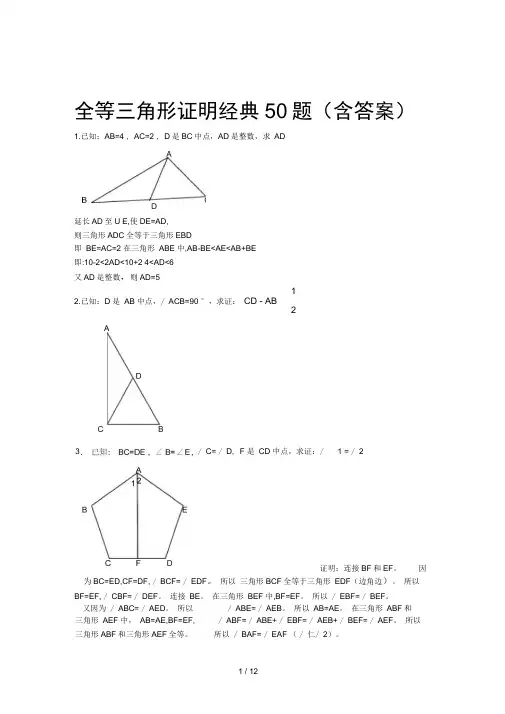
全等三角形证明经典50题（含答案）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数，则AD=512.已知：D 是 AB 中点，/ ACB=90 °，求证： CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF （边角边）。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点，求证：/ 1 = / 2证明：连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中， AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF （ / 仁/ 2）。
A3因为 EB = EF ,CE = CE ， 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图，四边形 ABCD 中，AB // DC ，BE 、CE 分别平分/ ABC 、/ BCD ，且点 E 在AD 上。
全等三角形题型归纳经典完整
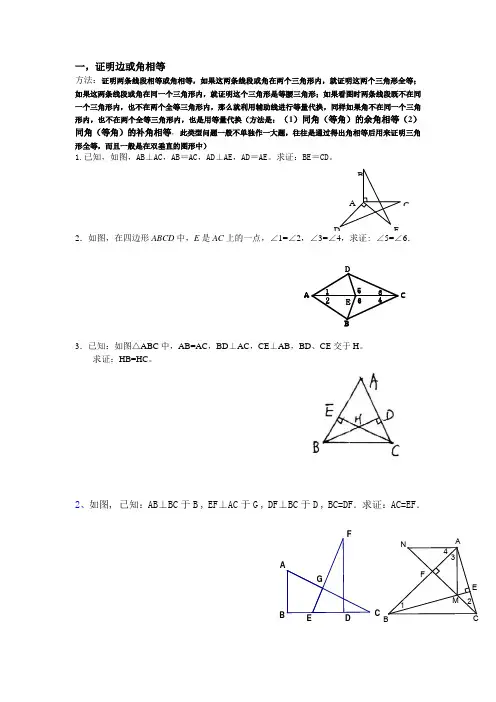
一，证明边或角相等方法：证明两条线段相等或角相等，如果这两条线段或角在两个三角形内，就证明这两个三角形全等；如果这两条线段或角在同一个三角形内，就证明这个三角形是等腰三角形；如果看图时两条线段既不在同一个三角形内，也不在两个全等三角形内，那么就利用辅助线进行等量代换，同样如果角不在同一个三角形内，也不在两个全等三角形内，也是用等量代换（方法是：（1）同角（等角）的余角相等（2）同角（等角）的补角相等，此类型问题一般不单独作一大题，往往是通过得出角相等后用来证明三角形全等，而且一般是在双垂直的图形中）1.已知，如图，AB ⊥AC ，AB ＝AC ，AD ⊥AE ，AD ＝AE 。
求证：BE ＝CD 。
2．如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．3．已知：如图△ABC 中，AB=AC ，BD ⊥AC ，CE ⊥AB ，BD 、CE 交于H 。
求证：HB=HC 。
2、如图, 已知：AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF ．求证：AC=EF ．A ED C B654321E DCBAFGE D CBAFMNE 1234EDC BA 二.证明线段和差问题 （形如：AB+BC=CD,AB=AD - CD)证明两条线段和等于另一条线段，常常使用截长补短法。
①截长法即为在这三条最长的线段截取一段使它等于较短线段中的一条，然后证明剩下的一段等于另一条较短的线段。
②补短法即为在较短的一条线段上延长一段，使它们等于最长的线段，然后证明延长的这一线段等于另一条较短的线段。
证明两条线段差等于另一条线段，只需把差化成和来解决即可。
1.如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．2、如图,已知：△ABC 中,∠BAC ＝90, AB ＝AC ,AE 是过A 一直线,且点B 、C 在AE 的异侧,BD ⊥AE 于D ,CE ⊥AE 于E . 求证：BD ＝DE ＋CE ；3、如图，AB ∥CD ，DE 平分∠ADC ，AE 平分∠BAD ，求证：AB=AD - CDP E D CB A三．证明线段的2倍或21关系 ( AB CE =2， MN BN =12） 1. 利用含30 角的直角三角形的性质证明例1. 已知，如图1，∆ABC 是等边三角形，在AC 、BC 上分别取点D 、E ，且AD ＝CE ，连结AE 、BD 交于点N ，过B 作BM AE ⊥，垂足为M ，求证：MN BN =12（提示：先证∠=BNE 60）2. 利用等线段代换（充分利用中点）例1．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ． 求证：BD =2CE ．3.转化为线段和问题，利用截长补短法例5. 已知：如图5，四边形ABCD 中，∠=D 90，对角线AC 平分∠BAD ，AC BC =，FE DCB A求证：AD AB12四．证明二倍角关系利用三角形外角和定理和等量代换如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠BD C BA。
初中数学 全等三角形经典题型50题(含答案)
全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
全等三角形经典题型50题带答案
全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB从D 做辅助线3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
全等三角形32道经典题
B O P A C Q E D
2.将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个 更小的正三角形，……如此继续下去，结果如下表： 所剪次数 正三角形个数 1 4 2 7 3 10 4 13 … … n an
则 an=________________（用含 n 的代数式表示）. O B E D C C A
9.如图（10），AC∥DE， BC∥EF，AC＝DE 求证：AF＝BD E C F A
A
C N M N E D B M E 图② D A
D B B
C
A 图①
10． 已知： 如图，B，C，E 三点在同一条直线上，AC ∥ DE ，AC CE ，ACD B ． 求证： △ABC ≌△CDE ． D A
三、简答题 1、已知:如图,AD=BC,AC=BD.求证:OD=OC
D O
C
A
B
2、如图，AB∥CD(1)用直尺和圆规作 C 的平分线 CP，CP 交 AB 于点 E(保留作图痕迹，不
写作法) (2)在(1)中作出的线段 CE 上取一点 F，连结 AF。要使△ACF≌△AEF，还需要添加 一个什么条件？请你写出这个条件(只要给出一种情况即可；图中不再增加字母和线段；不 要求证明)。 A B
A E C E’
A E D l E
A E D ’ D l D’ F ’ B
A E
B
l B C’ C (2)
’ B ′ C (3) ′ ′
C (4)
D
16.如图，在梯形 ABCD 中，AD∥BC，E 为 CD 中点，连接 AE 并延长 AE 交 BC 的延长线于 ′ 点 F．（1）求证：CF=AD；（2）若 AD=2，AB ′ =8，当 BC 为多少时，点 B 在线段 AF 的垂 直平分线上，为什么？ A D
三角形全等的判定专题训练题
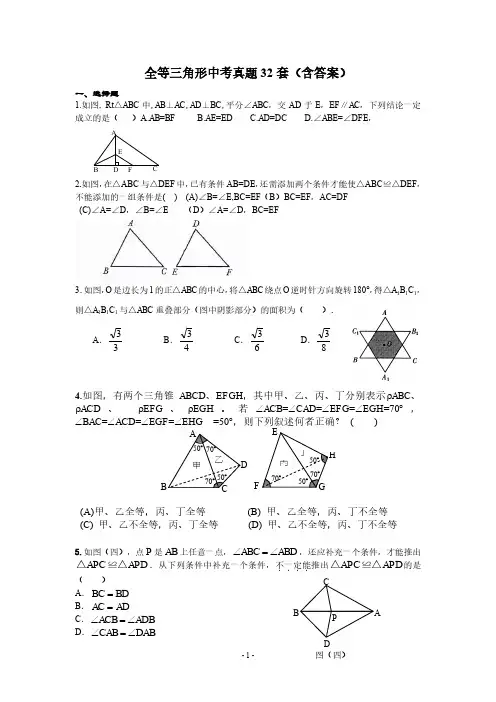
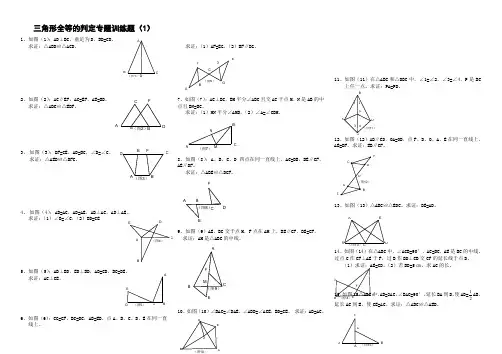
三角形全等的判定专题训练题（1）1、如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。
求证：△ABD ≌△ACD 。
2、如图（2）：AC ∥EF ，AC=EF ，AE=BD 。
求证：△ABC ≌△EDF 。
3、 如图（3）：DF=CE ，AD=BC ，∠D=∠C 。
求证：△AED ≌△BFC 。
4、 如图（4）：AB=AC ，AD=AE ，AB ⊥AC ，AD ⊥AE 。
求证：（1）∠B=∠C ，（2）BD=CE5、如图（5）：AB ⊥BD ，ED ⊥BD ，AB=CD ，BC=DE 。
求证：AC ⊥CE 。
6、如图（6）：CG=CF ，BC=DC ，AB=ED ，点A 、B 、C 、D 、E 在同一直线上。
求证：（1）AF=EG ，（2）BF ∥DG 。
7、如图（7）：AC ⊥BC ，BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。
求证：（1）MN 平分∠AMB ，（2）∠A=∠CBM 。
8、如图（8）：A 、B 、C 、D 四点在同一直线上，AC=DB ，BE ∥CF ，AE ∥DF 。
求证：△ABE ≌△DCF 。
9、如图（9）AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。
求证：AM 是△ABC 的中线。
10、如图（10）∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE 。
求证：AB=AC 。
11、如图（11）在△ABC 和△DBC 中，∠1=∠2，∠3=∠4，P 是BC上任一点。
求证：PA=PD 。
12、如图（12）AB ∥CD ，OA=OD ，点F 、D 、O 、A 、E 在同一直线上，AE=DF 。
求证：EB ∥CF 。
13、如图（13）△ABC ≌△EDC 。
求证：BE=AD 。
14、如图（14）在△ABC 中，∠ACB=90°，AC=BC ，AE 是BC 的中线，过点C 作CF ⊥AE 于F ，过B 作BD ⊥CB 交CF 的延长线于点D 。
全等三角形经典题型50题
全等三角形经典题型50题1. 已知:AB=4,AC=2, D是BC中点, AD是整数,求AD延长AD到E,使 DE-AD.则三角形ADC全等于三角形EBD印 BE-AC-2 在三角形ABE中,AB-BE<AE-AB+BE即:10-2<2AD<10+24<AD<6又AD是整数,则 AD=5AB2.已知: D是 AB中点,∠ACB=90°,求证: CD=123.已知: BC-DE,∠B -∠E,∠C-∠D, F是CD中点,求证:∠1-∠2证明:连接 BF和EF,因为BC=LD,CF=DF,∠BCF=∠EDF.所以三角形BCF全等于三角形EDF(边角边), 所以BF-EF∠CBF-∠DEF。
连接BE.在三角形BEF 中,BF-EF, 所以∠EBF=∠BEF。
又因为∠ABC-∠AED。
所以∠ABE=∠AEB, 所以 AB=AE, 在三角形ABF和三角形AEF中, AB=AEBF=EF.∠ABF-∠ABE+∠EBF=∠AEB+∠BEF=∠AEF, 所以三角形ABF 和三角形AEF 全等。
所以∠BAF-∠EAF(∠1=∠2).5. 已知:AD 平分∠BAC. AC=AB+BD.求证:∠B=2∠C证明: 在AC 上载取AE AB,连接ED ∵AD 平分∠BAC ∴/EAD/BAD 又∵AH AB, AD -AD ∴△AED ≌△ABD(SAS) ∴∠AED /B. DE D8 ∵AC -AB+BD AC AE+CH ∴CE-DE ∴∠C-∠IDC ∵∠AED-∠C ∠EDC-2∠C ∴∠B-2∠C12.如图,四边形ABCD 中, AB ∥DC,BE 、CE 分别平分∠ABC,∠BCD,且点E 在AD 上,求证:BC-AB+DC.4. 已知: ∠1=∠2,CD=DE,EF:AB,求证:EF=AC 证明: 过B 点、 作EG∥AC, 交 AD 延长线于 G 则∠DEG -∠DCA,∠DGE -∠2 又∵CD -DE ∴∠ADC≌AGDE(AAS)∴EGAC∵EF∥AB∴∠DFE=∠1∵∠1∠2∴∠DFE -∠DGE∴FF -EG ∴FF -AC6. 已知: AC 平分∠BAD. CE⊥ AB,∠B+∠D 180° , 求证: AE -AD+BE证明: 在AE 上取F.使EF-EB.连接 CF 因为 CE⊥AB 所 以∠CTB -∠CEF -90° 因为EB= EF : CE= CE,所以△CEB≌△CEF 所以∠B=∠CFE 因为∠B+∠D -180°, ∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC=AC 所以△ADC≌△AFC(SAS) 所以AD=AF 所以AE=AF +FE=AD+BE证明:在 BC 上截取BF-BA,连接EF.∠ABE=∠FBE,BE=BE,则∠ADL ≅△l ′DL (SAS ),∠EFB =∠A;AB 平行于CD.则∠A+∠D=180°,又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCECE=CE.故△FCE≌ADCE(AAS),FC -CD.所以,BC-BF+FC-AB+CD.13.已知: AB/ED, ∠EAB=∠BDE, AF-CD, EF-BC, 求证: ∠F-∠C14.已知:AB=CD,∠A=∠D,求证:∠B=∠C15. P 是∠BAC 平分数AD 上点,AC>AB,求证: PC-PB<AC-AB∠ABE=90-∠1=2∠C延长BE 交AC 于F因为, ∠1=∠2, BE ⊥AE所以,△ABF 是等腰三角形 AB=AF,BF=2BE ∠FBC=∠ABC-∠ABE=3∠C-2∠C=∠CBF-CF AC-AB-AC-AF-CF-BF-2BE17.已知,E 是 AB 中点,AF=BD,BD=5, AC=7, 求 DCAB∥ED,AE∥BD 推出AE=BD,又有AF-CD,EF-BC所以三角形AEF 全等于三角形DCB.所以:∠C -∠F 1: 证明: 设线段 AB,CD 所在的直线交于E,(当AD<BC 时,E 点是射线 BA. CD 的交点,当AD=BC 时,E 点是射线ABDC 的交点)。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题（含答案）1. 已知：AB=4,AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD ，则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE 〈AB+BE 即：10—2〈2AD 〈10+2 4〈AD 〈6 又AD 是整数，则AD=52. 已知:D 是AB 中点，∠ACB=90°,求证:12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
因为 BC=ED ，CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE.在三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB.所以 AB=AE 。
在三角形ABF 和三角形AEF 中，AB=AE,BF=EF ，∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2）。
ADBC4. 已知:∠1=∠2，CD=DE,EF//AB ，求证：EF=AC 证明：过E 点,作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD,求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证:AE=AD+BE证明： 在AE 上取F,使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°,∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC(SAS) 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图,四边形ABCD 中，AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
13. 如图，已知AB＝AC，AD＝AE，BD＝CE. 求证：∠3＝∠1＋∠2.5. 一块三角形玻璃样板不慎被小强同学碰破，成了四片完整的碎片(如图所示)，聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板．下列四个答案中考虑最全面的是( )A．带其中的任意两块去都可以B．带1、2 或2、3 去就可以了C．带1、4 或3、4 去就可以了D．带1、4 或2、4 或3、4 去均可16. 将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB ＝90°，∠A＝∠D＝30°，点 E 落在 AB 上，DE 所在直线交 AC所在直线于点 F.(1)求证：AF＋EF＝DE；(2)若将图①中的△DBE 绕点 B 按顺时针方向旋转角α，且 0°<α<60°，其他条件不变，请在图②中画出变换后的图形，并直接写出你在(1)中猜想的结论是否仍然成立；(3)若将图①中的△DBE 绕点 B 按顺时针方向旋转角β，且60°<β<180°，其他条件不变，如图③.你认为(1)中猜想的结论还成立吗？若成立，写出证明过程：若不成立，请写出 AF，EF与 DE之间的关系，并说明理由．板块一、三角形全等的判定与应用在AB、AC上各取一点E、D，使AE=AD，连接BD、CE相交于O再连结AO、BC，若1=2，则图中全等三角形共有哪几对？并简单说明理由．【巩固】如图所示，AB = AD，BC = DC，E、F在AC上，AC与BD相交于P．图中有几对全等三角形？请一一找出来，并简述全等的理由．板块二、三角形全等的判定与应用（2008年巴中市高中阶段教育学校招生考试）如图，AC∥DE，BC∥EF，AC = DE．求证：AF =BD．C（2008年宜宾市）已知：如图，AD = BC，AC = BD，求证：C = D．巩固】如图，AC、BD相交于O点，且AC = BD，AB = CD，求证：OA = OD（哈尔滨市2008 年初中升学考试）已知：如图，B、E、F、C四点在同一条直线上，AB = DC，BE =CF，B= C．求证：OA = OD．已知，如图，AB=AC，CE⊥AB，BF⊥AC，求证：BF =CEE、F分别是正方形ABCD的BC、CD边上的点，且BE = CF．求证：AE⊥BF．巩固】E、F、G分别是正方形ABCD的BC、CD、AB边上的点，GE⊥EF，GE = EF．求证：BG+ CF = BC在凸五边形中，B = E，C = D，BC = DE，M为CD中点．求证：AM⊥CD如图，点M为正三角形ABD的边AB所在直线上的任意一点（点B除外），作DMN = 60，射线MN与∠DBA外角的平分线交于点N，DM与MN有怎样的数量关系?【巩固】如图，点M为正方形ABCD的边AB上任意一点，MN⊥DM且与∠ABC外角的平分线交于点N，MD与MN有怎样的数量关系？D C已知：如图，ABCD 是正方形，∠FAD=∠FAE. 求证：BE+DF=AE. 如图所示，ABC 是边长为1的正三角形，BDC 是顶角为120o 的等腰三角形，以D 为顶点作一个60o 的MDN ，点M 、 N 分别在AB 、 AC 上，求AMN 的周长．五边形 ABCDE 中，AB=AE ，BC+DE=CD ，∠ABC+∠AED=180°，求证：AD 平分∠CDE如图，AD ⊥AB ，CB ⊥AB ， DM=CM=a ，AD=h ，CB=k ， ∠AMD=75°，∠BMC=45°，则 AB 的长 k+hC. 2D. hCA板块四、与角平分线有关的全等问题 如图，已知ABC 的周长是21 ，OB ， OC 分别平分ABC 和ACB ，OD ⊥ BC 于D ，且OD = 3 ，求 ABC 的面积．在ABC 中， D 为BC 边上的点，已知BAD = CAD ， BD = CD ，求证： AB = AC 已知ABC 中，AB = AC ，BE 、CD 分别是ABC 及ACB 平分线．求证：CD =BE ． 已知ABC 中，A = 60o ，BD 、CE 分别平分ABC 和ACB ，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．E如图，已知E 是AC 上的一点，又1 =2 ，3 =4 ．求证： ED = EB ．（“希望杯”竞赛试题）长方形 ABCD 中，AB=4，BC=7，∠BAD 的角平分线交 BC 于点 E ，EF ⊥ED 交 AB 于 F ，则 EF= ___________ ．【巩固】如图，在ABC 中， AD 交BC 于点D ，点E 是BC 中点， EF ∥ AD 交CA 的延长线于点F ，交AB 于点G ，若BG = CF ，求证： AD 为BAC 的角平分线． AB - AC PB -PC 如图所示，已知ABC 中， AD 平分BAC ， E 、 F 分别在BD 、 AD 上．DE =CD ，EF =AC ．求证： EF ∥ AB巩固】在ABC 中， AB AC ， AD 是 BAC 的 平 分 线 ． P 是 AD 上 任 意 一 点 ． 求 证 ：D BD C如图，在ABC中，B = 2C，BAC的平分线AD交BC与D．求证：AB + BD = AC如图所示，在ABC中，AC AB，M为BC的中点，AD是BAC的平分线，若CF⊥AD且交AD的MF =1(AC-AB)延长线于F，求证2．【巩固】如图所示，AD是ABC中BAC的外角平分线，CD⊥AD于D，E是BC的中点，求证DE=12(AB+AC)．DE∥AB且巩固】如图所示，在ABC中，AD平分BAC，AD=AB，CM⊥AD于M，求证AB+AC=2AM如图，ABC中，AB=AC，BD、CE分别为两底角的外角平分线，AD⊥BD于D，AE⊥CE于E．求证：AD= AE．【巩固】已知：AD 和BE 分别是△ABC 的∠CAB 和∠CBA 的外角平分线，CD ⊥AD ，CE ⊥BE ，求DE = 1(AB + BC +CA )证：⑴ DE ∥AB ；⑵ 2 ．在ABC 中，MB 、 NC 分别是三角形的外角ABE 、 ACF 的角平分线， AM ⊥BM ，AN ⊥CN 垂巩固】在ABC 中，MB 、NC 分别是三角形的内角ABC 、ACB 的角平分线，AM ⊥ BM ，AN ⊥ CN巩固】(北京市中考模拟题)如图，在四边形ABCD 中， AC 平分BAD ，过C 作CE ⊥ AB 于E ， AE = 1(AB + AD )并且 2 ，则ABC + ADC 等于多少？如图， A + D =180， BE 平分ABC ， CE 平分BCD ，点E 在AD 上 探讨线段 AB 、 CD 和BC 之间的等量关系．足分别是M 、 N ．求证： MN ∥BC ，MN = 1(AB + AC +BC )垂足分别是M 、 N ．求证： MN ∥BC ，MN = 1(AB + AC -BC )B探讨线段BE 与CE 之间的位置关系．版块一、倍长中线AM 1(AB +AC ) 已知： ABC 中， AM 是中线．求证： 2【巩固】(2002年通化市中考题)在ABC 中，AB = 5, AC = 9 ，则BC 边上的中线AD 的长的取值范围是 什么？ 如图， ABC 中， AB <AC ， AD 是中线．求证：DAC <DAB ． 如图，已知在ABC 中， AD 是BC 边上的中线， E 是AD 上一点，延长BE 交AC 于F ，AF =EF ， 已知△ABC ，∠B=∠C ，D ，E 分别是AB 及AC 延长线上的一点，且BD=CE ，连接DE 交底BC 于G ， 求证 GD=GE．求证： AC = BE DC已知AM 为ABC 的中线， AMB ， AMC 的平分线分别交 AB 于 E 、交AC 于 F ．求证： BE + CF EF在Rt ABC 中，A =90，点D 为BC 的中点，点E 、F 分别为AB 、 AC 上的点，且ED ⊥ FD ．以 线段BE 、 EF 、 FC 为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形或钝角三巩固】如图所示，在ABC 中，D 是BC 的中点，DM 垂直于DN ，如果BM 2+CN 2 =DM 2+DN 2，（ 2008年四川省初中数学联赛复赛·初二组）在RtABC 中，F 是斜边AB 的中点，D 、E 分别在边CA 、 CB 上，满足DFE =90 ．若AD =3 ， BE =4 ，则线段DE 的 长 度 为角形？AD C求证AD 2 = 14(AB 2 + AC 2)A版块二、中位线的应用AD是ABC的中线，F是AD的中点，BF的延长线交AC于E．求证：如图所示，在ABC中，AB = AC，延长AB到D，使BD = AB，E为AB的中点，连接CE、CD，求证CD = 2EC【巩固】已知△ABC 中，AB=AC，BD为AB的延长线，且BD=AB，CE为△ABC 的AB边上的中线．求证CD=2CE已知：ABCD是凸四边形，且AC<BD．E、F分别是AD、BC的中点，EF交AC于M；EF交BD于N，AC 和BD 交于G 点．求证：∠GMN>∠GNM．DF CAC = BC在ABC中，ACB=90， 2 ，以BC为底作等腰直角BCD，E是CD的中点，求证：AE⊥EB且AE = BE．如图，在五边形ABCDE中，ABC = AED = 90，BAC = EAD，F为CD的中点．求证：BF = EF（“祖冲之杯”数学竞赛试题，中国国家集训队试题）如图所示，P是ABC内的一点，PAC = PBC，过P作PM⊥AC于M，PL⊥BC于L，D为AB的中点，求证DM =DL．（全国数学联合竞赛试题）如图所示，在ABC中，D为AB的中点，分别延长CA、CB到点E、F，使DE=DF．过E、F分别作直线CA、CB的垂线，相交于点P，设线段PA、PB的中点分别为M、N．求证：(1) DEM≌FDN；(2) PAE = PBFC习题1】如图，已知AC = BD ， AD ⊥ AC ，BC ⊥BD ，求证：AD =BC【习题 2】点 M ，N 在等边三角形 ABC 的 AB 边上运动，BD=DC ，∠BDC=120°，∠MDN=60°，求 证 MN=MB+NC ．AB =3AC ，BAC 的平分线交BC 于D ，过B 作BE ⊥ AD ， E 为垂足，求B 证： AD = DE ．习题4】如图，在ABC 中， AB + BD = AC ， BAC 的平分线AD 交BC 与D ．求证： B = 2C 习题 3】在△ABC 中， EFP ACAC ED C习题5】如图，在等腰ABC中，AB = AC，D是BC的中点，过A作AE⊥DE，AF⊥DF，且AE = AF．【习题6】如图，已知在ABC中，AD是BC边上的中线，E是AD上一点，且BE = AC，延长BE交AC于F，AF与EF相等吗？为什么？习题7】如右下图，在ABC 中，若B=2C，AD⊥BC，E为BC边的中点．求证：AB=2DE．求证：EDB =FDC。