初中数学中的格点问题 PPT

授课设计教师学生科目数学上课时间课次 1授课内容中考中的格点图形问题授课重难点解题方法授课设计：近来几年来，有关格点问题已成为中考的亮点，这类问题题型多样，形式爽朗，主要观察同学们的直觉推理能力和问题研究能力．格点问题操作性强、兴趣性浓，表现了新课标的“在‘玩’中学，在学中思，在思中得”的崭新理念．下面就中考中的几类格点问题归纳以下，望能对学习有所帮助．一、格点中的对称问题例 1 （绍兴市）如图 1，在网格中有两个全等的图形 (阴影部分 )，用这两个图形拼成轴对称图形，试分别在图(1) 、(2) 中画出两种不同样的拼法．图1图2二、格点中的画图问题例 2 （黑龙江鸡西市）如图3，在网格中有一个四边形图案．（1）请你画出此图案绕点 O 顺时针方向旋转 900， 1800，2700的图案，你会获取一个美丽的图案，千万不要将阴影地址涂错；图 3图4（2）若网格中每个小正方形的边长为l ，旋转后点 A 的对应点依次为 A1、 A2、A3，求四边形 AA1A2A3的面积；(3)这个美丽图案可以说明一个出名结论的正确性，请写出这个结论．三、格点中的坐标问题例3 （苏州市）如图 5．围棋盘的左下角表现的是一局围棋比赛中的几手棋．为记录棋谱方便，横线用数字表示．纵线用英文字母表示，这样，黑棋①的地址可记为(C，4)，白棋②的地址可记为( E， 3) 则白棋⑨的地址应记为＿＿＿．图 5四、格点中的相似问题例 4 （福州市罗源平潭）如图成的相似三角形有（）A ． 4 对B ． 3 对C． 2 对6，在 7×12 的正方形网格中有一只可爱的小狐狸，算算看画面中由实线组DD ．1 对A C F析解：本题是一道以网格为背景的结论研究性问题， B E J H在正方形网格中画了一只可爱的小狐狸，增强了题目G I R L的兴趣性．由网格的特色结合勾股定理，可以获取三角图6形三边的长，从而利用“三边对应成比率，两三角形相似”的判断来求解．．五、格点中的位似问题例5 （广东省）如图 7，图中的小方格都是边长为 1 的正方形，△ ABC 与△ A′B′C′是关于点 O 为位似中心的位似图形，它们的极点都在小正方形的极点上．（1）画出位似中心点 O；（2）求出△ ABC 与△ A/B/C/的位似比；（ 3）以点 O 为位似中心，再画一个△A1B1C1，使它与△ ABC的位似比等于．C/ C/C1B/ C B/ CA/BA/B1 BA A1 A O 图 7 图 8六、格点中的面积问题例 6 （浙江湖州市）一青蛙在如图8×8 的正方形（每个小正方形的边长为 1）网格的格点（小正方形的极点）上跳跃，青蛙每次所跳的最远距离为 5 ，青蛙从点A开始连续跳六次正好跳回到点 A，则所组成的封闭图形的面积的最大值是_______．图 9析解：本题以青蛙这一幽默且有益的动物为背景设计题目，增加了题目的兴趣性．解题时涉及无理数、勾股定理的应用、图形面积的计算等知识．只要正确画出图形，再运用割补法即可求得面积为 12．七、格点中等腰三角形问题例 7 （重庆市）以下列图，A、 B 是 4×5 网络中的格点，网格中的每个小正方形的边长为晰标出使以Ａ、B、C 为极点的三角形是等腰三角形的所有格点 C 的地址．1，请在图中清A AB B图10 图11析解：依照网格的特色及等腰三角形的有关知识易得，AB 只能为一腰，且AB= 13 ，由勾股定理即可知点C1、 C2、 C3吻合要求（如图11）．八、格点中的拼图问题例 8 （北京市）请阅读以下资料：问题：现有 5 个边长为画出切割线并在正方形网格图1 的正方形，排列形式如图①，请把它们切割后拼接成一个新的正方形．(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形．要求：小东同学的做法是：设新正方形的边长为x(x＞ 0)．依题意，割补前后图形的面积相等，有x2=5 ，解得x= 5 ．由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长．于是，画出如图②所示的分割线，拼出如图③ 所示的新正方形．图①图②图③图④图⑤图12请你参照小东同学的做法，解决以下问题：现有 10 个边长为 1 的正方形，排列形式如图④，请把它们切割后拼接成一个新的正方形．要求：在图④中画出切割线，并在图⑤的正方形网格图 (图中每个小正方形的边长均为 1)中用实线画出拼接成的新正方形．说明：直接画出图形，不要求写解析过程．析解：本题是一道综合型网格作图试题，涉及到无理数、勾股定理等知识，主要观察同学们的计算能力、着手操作能力．类比小东的作法，可设新正方形的边长为x(x>0)，便有 x2=10 ，解得 x=10 ．由此可知，新正方形得边长等于两个小正方形组成得矩形对角线得长．于是，画出如图②所示的切割线，拼出如图③所示的新正方形．图 13图14温州历年中考中的格点问题19．（ 2009?温州） ( 本题 8 分 ) 在所给的 9×9方格中，每个小正方形的边长都是1．按要求画平行四边形，使它的四个极点以及对角线交点都在方格的极点上．(1) 在图甲中画一个平行四边形，使它的周长是整数； (2) 在图乙中画一个平行四边形，使它的周长不是整数． ( 注：图甲、图乙在答题纸上 )19、（ 2011?温州）（本题8 分）七巧板是我们祖先的一项优异创立，用它可以拼出多种图形，请你用七巧板中标号为○1 ○2 ○3的三块板（如图1）经过平移、旋转拼成图形。

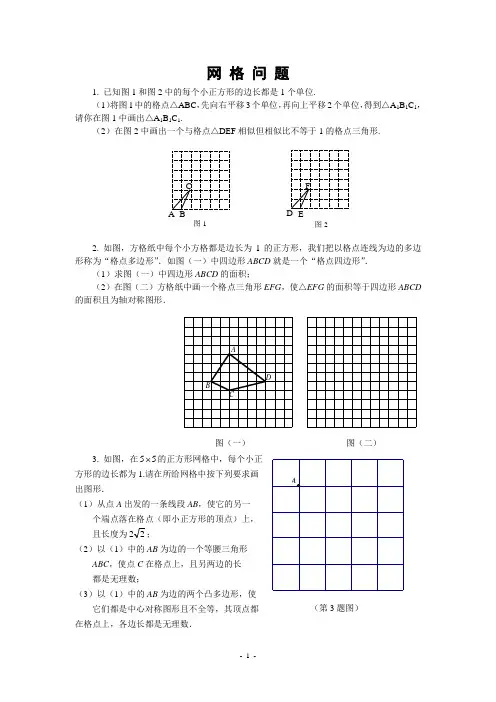
网 格 问 题1. 已知图1和图2中的每个小正方形的边长都是1个单位. （1）将图1中的格点△ABC ，先向右平移3个单位，再向上平移2个单位，得到△A 1B 1C 1，请你在图1中画出△A 1B 1C 1.（2）在图2中画出一个与格点△DEF 相似但相似比不等于1的格点三角形.2. 如图，方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．如图（一）中四边形ABCD 就是一个“格点四边形”．（1）求图（一）中四边形ABCD 的面积；（2）在图（二）方格纸中画一个格点三角形EFG ，使△EFG 的面积等于四边形ABCD 的面积且为轴对称图形．DCBA图（一） 图（二）3. 如图，在55 的正方形网格中，每个小正 方形的边长都为1.请在所给网格中按下列要求画 出图形．（1）从点A 出发的一条线段AB ，使它的另一个端点落在格点（即小正方形的顶点）上， 且长度为22；（2）以（1）中的AB 为边的一个等腰三角形ABC ，使点C 在格点上，且另两边的长 都是无理数；（3）以（1）中的AB 为边的两个凸多边形，使它们都是中心对称图形且不全等，其顶点都 在格点上，各边长都是无理数．图2 F E A B C 图1 （第3题图）4. 下面的方格纸中，画出了一个“小猪”的图案，已知每个小正方形的边长为1．（1）“小猪”所占的面积为多少？（2）在上面的方格纸中作出“小猪”关于直线DE 对称的图案（只画图，不写作法）；（3）以G 为原点，GE 所在直线为x 轴，GB 所在直线为y 轴，小正方形的边长为单位长度建立直角坐标系，可得点A 的坐标是（_______，_______）．5. 图(1)是一个10×10格点正方形组成的网格. △ABC 是格点三角形(顶点在网格交点处),请你完成下面两个问题:(1) 在图(1)中画出与△ABC 相似的格点△A 1B 1C 1和△A 2B 2C 2, 且△A 1B 1C 1与△ABC 的相似比是2, △A 2B 2C 2与△ABC 的相似比是22.(2) 在图(2)中用与△ABC 、△A 1B 1C 1、△A 2B 2C 2全等的格点三角形(每个三角形至少使用一次), 拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.【解说词】6. 如图，有一条小船，（1） 若把小船平移，使点A 平移到点B ，请你在图中画出平移后的小船；（5分） （2） 若该小船先从点A 航行到达岸边L 的点P 处补给后，再航行到点B ，但要求航程最短，EC D GB FA试在图中画出点P 的位置（3分）7. ⑴如图6，在方格纸中如何通过平移或旋转这两种变换，由图形A 得到图形B ，再由图形B 得到图形C （对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转中心、旋转方向和旋转角度）；⑵如图6，如果点P 、P 3的坐标分别为（0，0）、（2，1），写出点P 2的坐标； ⑶图7是某设计师设计图案的一部分，请你运用旋转变换的方法，在方格纸中将图形绕点O 顺时针依次旋转90°、180°、270°，依次画出旋转后所得到的图形，你会得到一个美丽的图案，但涂阴影时不要涂错了位置，否则不会出现理想的效果，你来试一试吧！注：方格纸中的小正方形的边长为1个单位长度.图7图68. 在如图10所示的平面直角坐标系中，已知△ABC 。

一、网格题型在中考数学中的10大考点梳理网格问题，近年来在一些省市的中考试卷中频频出现，这类问题虽然出现在小网格中，却隐藏着大智慧，从中可以开发智力，发展思维．笔者以中考试题为例，说明小网格中的大智慧．一、正方形网格（一）全网格形全网格形是指有完整的网格的题型．1．网格中求坐标例1：如图1，在一单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…都是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A t(2，0)，A2（1，－1），A3(0，0)，则依图中所示规律，A2012的坐标为________．分析：由于2012是4的倍数，故A1~A4；A5～A8；…每4个为一组，可见，A2012在x轴上方，横坐标为2，再根据纵坐标变化找到规律即求得纵坐标为1006．答案：(2，1006)2．网格与等腰三角形例2：如图2所示的正方形网格中，网格线的交点称为格点°已知A、B是两格点，如果C 也是图中的格点，且使得△ABC为等腰三角形，则点G的个数是()(A)6(B)7(C)8(D)9分析：有两种情况：①AB为等腰△ABC底边，C在A B的中垂线上，因此，符合条件的C点有4个；②AB为等腰ABC其中的一条腰，符合条件的C点有4个，应选C．本题考查了等腰三角形的判定，解答本题关键是根据题意，画出符合实际条件的图形．3．网格与直角三角形例3：如图3，在网格中有一个直角三角形（网格中的每个小正方形的边长均为1个单位长度）．若以该三角形一边为公共边画一个新三角形与原来的直角三角形一起组成一个等腰三角形，要求新三角形与原来的直角三角形除了有一条公共边外，没有其它的公共点，新三角形的顶点不一定在格点上．那么符合要求的新三角形有()(A)4个(B)6个(C)7个(D)9个分析：根据题意可知：如图4，以原三角形AB边为公共边的三角形有4个，分别如图上D1，D2，D3，D4；以原三角形BC边为公共边的三角形有2个，分别如图上D5，D6；以原三角形AC边为公共边的三角形只有1个，如图上D．符合要求新三角形有7个，选C例4：如图5是5×5的正方形网格，△ABC的顶点都在小正方形的顶点上，像△ABC这样的三角形叫格点三角形．画与△ABC有一条公共边且全等的格点三角形，这样的格点三角形最多可以画出_______个．分析：如图6，以BC为公共边可画出△BDC，△BEC，△BFC三个三角形和原三角形全等；以AB为公共边可画出三个三角形△ABC、△ABM、△AB H和原三角形全等，所以可画出6个．5．网格与相似例5：图7所示4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是()[来源学*科*网][来源学科网Z XX K]分析：根据勾股定理，得BC＝，AB，AC；根据勾股定理的逆定理可判断△ABC为直角三角形，∠ABC＝90°，BC：AB＝1：2．在四个图形中，显然答案B中的三角形为直角三角形且两条直角边的比为1：2，选B．例6：如图8，在3×5的正方形网格中，每个小正方形的边长为1，求图中点A到P Q的距离A H的长．分析：连结A P，AQ组成一个三角形．你可以用长方形面积减去三个直角三角形求得[来源学科网]出△A P Q的面积，而S△A P Q＝12P Q×A H，P Q的长用勾股定理计算，求得答案为755．7．网格中求三角函数[来源:Z xx k.C o m]例7：如图9，在正方形网格中有△ABC，则s i n∠ABC的值等于()（A）31010（B）1010（C）13（D）10分析：首先利用勾股定理分别算出AB、BC、AC的长度，再利用勾股定理的逆定理得出∠ACB＝90°，最后根据锐角三角函数的定义求出s i n∠ABC的值，选B．8．网格与圆例8：如图10，边长为1的小正方形构成的网格中，半径为1的⊙O 的圆心O 在格点上，点A 、B 、C 、E 也都在格点上，CB 与⊙O 相交于点D ，连结ED ，则∠AED 的正切值等于_______．分析：本题是锐角三角函数的定义和圆周角的运用，解答本题的关键是利用同弧所对的圆周角相等把求∠AED 的正切值转化成求∠ACB 的正切值．tan ∠AED ＝tan ∠ABC ＝12AC AB ．（二）局部网格形局部网格形指是网格图案的一部分，需要通过添线补全网格的题型．例9：如图11(1)，每个小正方形的边长为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为()(A )90°(B )60°(C )45°(D )30°分析：先把局部网格补全成如图11(2)所示，易见△ACD 与△CBE 全等，可得出AC ＝BC ，∠ACB ＝90°，所以∠ABC ＝45°．选C ．二、长方形网格例10：如图12，在长方形网格中，每个小长方形的长为2，宽为1，A、B两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C 个数是()(A)2(B)3(C)4(D)5[来源学科网]分析：底和高分别是4和1的有两个，底和高分别是2和2的有两个，选C．二、中考网格型试题赏析近几年中考中，网格型试题可谓大放异彩，这类试题构思精巧、形式活泼，能很好地考查图形变换、勾股定理、相似等数学知识，体现分类讨论、数形结合等重要的数学思想，当网格作为背景与双曲线、抛物线、圆、三角形结合时，更会出现许多让人意想不到的思路、方法，使我们在解题中感受到无穷的乐趣，本文撷取其中的几例进行解析，供参考．一、网格与双曲线结合例1：在边长为1的4×4方格上建立直角坐标系（如图1），在第一象限内画出反比例函数16y x =、6y x =、4y x=的图象，它们分别经过方格中的一个格点、二个格点、三个格点；在边长为1的10×10方格上建立直角坐标系（如图2），在第一象限内画出反比例函数的图象，使它们经过方格中的三个或四个格点，则最多可画出()条．(A )12(B )13(C )25(D )50分析：易知系数k 为合数，且能分解成两个均不超过10的正整数的乘积的形式．如4＝1×4＝2×2，则反比例函数4y x=的图象经过以下3个格点：(1，4)，(2，2)，(4，1)．6＝1×6＝2×3，则反比例函数6y x =的图象经过以下4个格点：(1，6)，(2，3)，(3，2)，(6，1)．经过尝试，符合条件的k 值共有13个，分别为：4，6，8，9，10，12，16，18，20，24，30，36，40．所以，经过方格中的三个或四个格点的反比例函数的图象最多可以画出13条．故选B ．二、网格与抛物线结合例2：已知图3中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，请你在图中任意画一条抛物线，问所画的抛物线最多能经过81个格点中的多少个？()(A )6(B )7(C )8(D )9分析：我们先解决如下问题：对于抛物线y ＝ax 2＋bx ＋c ，当a 、b 、c 满足什么条件时，当x 取任意整数时，函数值y 都是整数？（为叙述方便，不妨假设抛物线开口向上．）当x ＝0时，y ＝c ；当x ＝l 时，y ＝a ＋b ＋c ．∴c 为整数，a ＋b ＋c 为整数，∴a ＋b 必为整数，又∵当x ＝2时，y ＝4a ＋2b ＋c ＝2a ＋2(a ＋b )＋c 是整数，∴2a 必为整数，∴a 应为12的整数倍，即a ＝12，1，32，2，…从对称的角度考虑，建立如图4所示的平面直角坐标系．(1)若抛物线的顶点在格点上，要使抛物线尽可能多地经过格点，显然应使抛物线过原点．所画抛物线y ＝ax 2（n ＝12，1，32，2，…）最多能经过5个格点．(2)若抛物线的顶点不在格点上，要使抛物线尽可能多地经过格点，显然应使抛物线），＝ax 2＋bx ＋c 过原点和(1，0)．所画抛物线y ＝ax (x －1)（a ＝12，1，32，2，…）最多能经过8个格点．此时a ＝12，这8个格点分别为：(－3，6)，（－2，3），（－1，1），(0，0)，(1，0)，(2，1)，(3，3)，(4，6)．[来源学&科&网Z&X &X &K]综上所述，抛物线最多能经过81个格点中的8个，故选C ．三、网格与圆结合例3：请你在12×12的网格图形中任意画一个圆，则所画的圆最多能经过169个格点中的____个格点．分析：从对称的角度考虑，建立如图5所示的平面直角坐标系．(1)如图5，若圆心在格点上，要使圆尽可能多地经过格点，显然应使圆心过原点，所画圆最多能经过12个格点，此时圆的半径为5．这12个格点分别为：(0，5)，(3，4)，(4，3)，(5，0)，[来源学§科§网](4，－3)，（3，－4），（0，－5），（－3，－4），(－4，－3)，（－5，0），（－4，3），（－3，4）．(2)如图6，若圆心不在格点上，要使圆尽可能多地经过格点，显然应使圆心过（12，12），所画圆最多能经过16个格点，此时圆的半径为2，这16个格点分别为：(2，6)，(4，5)，(5，4)，(6，2)，（6，－1），（5，－3），（4，－4），（2，－5），（－1，－5），（－3，－4），（－4，－3），(－5，－1)，（－5，2），（－4，4），（－3，5），（－1，6）．综上所述，所画的圆最多能经过169个格点中的16个格点．四、网格与三角形结合例4：如图7，将△ABC 放在每个小正方形的边长为1网格中，点A 、B 、C 均落在格点上．(1)△ABC 的面积等于____；(2)若四边形DEF G 是△ABC 中所能包含的面积最大的正方形，请你在如图7所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图的方法．分析：(1)S △ABC ＝12×4×3＝6；(2)如果正方形的一边落在三角形的一边上，其余两个顶点分别在三角形的另外两条边上，则这样的正方形面积是最大的．如图8，在△ABC 中，AB ＝c ，AB 边上的高CN ＝h c ，△ABC 的面积为S ，正方形的一边DE 落在AB 上，其余两个顶点F 、G 分别在BC 、AC 上．设正方形DEF G 的边长是x．所以，图8中正方形一边落在AB 边上，另两个顶点落在其他两边上时，121212744x ==+；图8中正方形一边落在BC边上，另两个顶点落在其他两边上时，图8中正方形一边落在AC 边上，另两个顶点落在其他两边上时，[来源学科网Z|X X|K]∴当正方形一边落在BC边上时，正方形DEF G的面积最大．画法一：如图9，在AB上任取一点P，作P Q⊥BC于点Q，以P Q为一边在△ABC内部画正方形P QMN；作射线BN交AC于点D，过点D作D G⊥BC于点G，作DE⊥D G交AB 于点E，过点E作EF⊥BC于点F，则四边形DEF G即为所求．证明：由画图过程易得四边形DEF G为矩形，∵D G⊥BC，NM⊥BC，∴D G//NM，画法二：如图10，取格点P，连结P C，过点A画P C的平行线，与BC交于点Q，连结P Q 与AC相交得点D；过点D画CB的平行线，与AB相交得点E，分别过点D、E画P C的平行线，与CB相交得点G、F，则四边形DEF G即为所求．证明：由画图过程易得四边形DEF G为平行四边形，[来源学科网]由格点P的位置易判断P C＝CB，且P C⊥CB，∴D G⊥CB，∴平行四边形DEF G为矩形。

中考中的格点三角形问题在正方形的方格纸中，每个小方格的顶点叫做格点，以格点的连线为边的三角形叫做格点三角形.在初中数学教材中都提到过格点三角形，并且近两年中考中都出现过一些题目，基本上是有关全等三角形、相似三角形、面积等问题，现特举例说明.图1例1 在大小为4×4的正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请在图1中画一个△A１B１C１∽△ABC （相似比不为1），且△A１B１C１都在单位正方形的顶点上.（上海市中考题）略解：AB=，BC=2,AC=,如图1，只要使Ａ１Ｂ１=2，Ｂ１Ｃ１=2,Ａ１Ｃ１=2或Ａ１Ｂ１=1,B１C１=，A１C１=等.例2 如图2，在正方形的网格上有两个三角形△Ａ１Ｂ１Ｃ１和△Ａ２Ｂ２Ｃ２，则△Ａ１Ｂ１Ｃ１与△Ａ２Ｂ２Ｃ２的面积比等于（）．图2A.4∶1B.3∶1C.5∶2D.5∶3（山东省中考题）略解：先找到两个三角形△Ａ１Ｂ１Ｃ１与△Ａ２Ｂ２Ｃ２是等高的，所以面积之比是两对应边Ｂ１Ｃ１与Ｂ２Ｃ２之比，为5∶2.例3 在方格纸中，每个小方格的顶点叫做格点，以格点的连线为边的三角形叫做格点三角形，请你在图310×10的方格中，画出两个相似但不全等的格点三角形，并加以证明.要求：所画三角形是钝角三角形，并标明相应字母.（2001年山西省中考题）略析：这样的三角形很多，找到两个相似的格点三角形（如图3），然后求出每个格点三角形的边长，证出三对对应边成比例或两对对应角相等，那么这两个三角形相似.图3例4 在方格纸上有一个△ＡＢＣ，它的顶点位置如图4所示，则这个三角形是________________三角形.（江西省中考题）图4略解：得出AB=AC=，是等腰三角形.例5 如图5所示，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形：（1）使三角形的三边长分别为3、2、（在图5中画一个即可）.（2）使三角形为钝角三角形且面积为2（在图6中画一个即可）.略解：（1）这样的三角形（如图5）为△ABC.图5 图6（2）如图6，△DEF即为所求.格点三角形的问题不但考查了相似三角形的判定与性质定理、勾股定理、正方形的性质、钝角三角形、等腰三角形的性质、面积，而且考查了同学们的运算、画图、推理等技能，并且考查了学生分析问题的能力.通过格点三角形的问题的学习，发现了在数学学习中要善于运用课本上的习题，并能进行归纳、引申、变式训练，以来培养同学们的创新意识及创新能力.。

学科：奥数教学内容：格点与面积生活中我们常借助一些工具来迅速简便的解决一些问题，如为了能捕到鱼，人们制作了鱼钩和网。

同样在数学的学习中，为了更好的解决问题聪明的人类也创造了一些“工具”。

这一讲我们主要介绍利用格点求几何图形的面积。

先来介绍什么是“格点”。

见下图：这是一张由水平线和垂直线组成的方格纸，我们把水平线和垂直线的交点称为“格点”，水平线和垂直线围成的每个小正方形称为“面积单位”。

图中带阴影的小方格就是一个面积单位。

借助格点图，我们可以很快的比较或计算图形的面积大小。

利用格点求图形的面积通常有两种思路，一是直接将图形分成若干个面积单位，然后通过计算有多少个面积单位来求图形面积；二是将某些图形转化成长方形的面积来求。

当然还可以将这两种方法结合起来，求出某些较复杂图形的面积。

例1 计算下图中各图形的面积：分析：先仔细观察图中的每个图形，选择方法。

显然第一、三、六图可以直接数出包含多少个面积单位即可。

而二、四、五图显然不适合用数单位面积的方法来求面积，可以采用虚线把这些图形扩展或割补成长方形，通过求长方形面积来求这些图形面积。

解答：（1）图中长方形包括3×2=6（个）面积单位，所以它的面积为6。

（2）将图中平行四边形割补成一个长方形，长方形的面积为3×2=6，而平行四边形的面积等于长方形面积，所以平行四边形的面积为3×2=6。

（3）将图中三角形用虚线分成3块，它包含有1个面积单位和2个面积单位的一半，合起来有2个面积单位，所以它的面积为2。

（4）图中将三角形扩展成一个长方形，长方形的面积为3×2=6，而三角形面积为长方形面积的一半，则三角形面积为3。

（5）将图中梯形的互相平行的一组对边延长，补出一个和原来梯形方向颠倒，但面积一样的梯形，形成一个大的长方形。

长方形的面积为（2＋4）×3=18，而梯形的面积为长方形的面积的一半。

所以梯形的面积为：（2＋4）×3÷2=9。