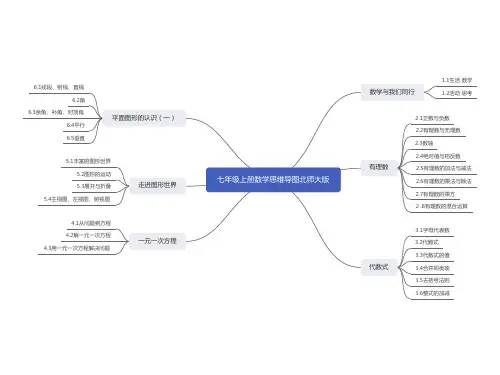
北师大版七年级上册第二章有理数章节思维导图

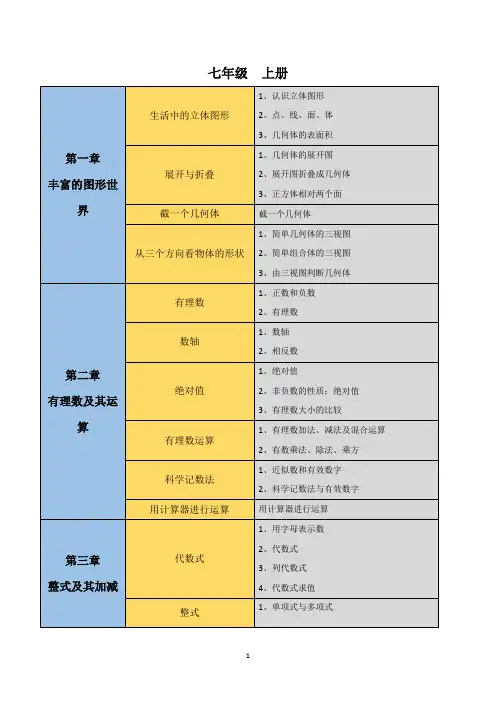
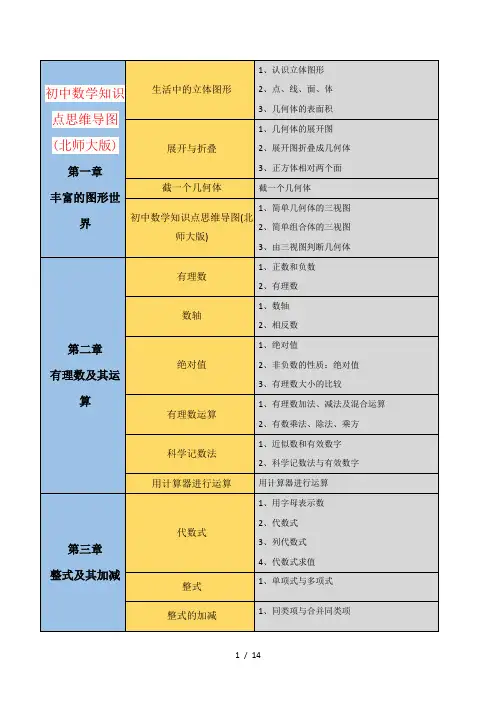
七年级数学上册思维导图第一章有理数有理数是指可以表示为两个整数之比的数，包括整数、分数、正有理数、负有理数等。

其中，整数按照定义进行分类，分数则按照性质和符号进行分类，正有理数和负有理数则按照符号进行分类。

相反数是指只有符号不同的两个数，绝对值是指数在数轴上与原点的距离。

倒数是指乘积为1的两个数互为倒数，科学记数法是把一个数表示为a×10^n的形式（其中1≤a<10，n是正整数）的记数方法。

有理数的加、减、乘、除和乘方都有相应的法则和符号，包括加法交换律、减法法则、乘法交换律、除法法则、加法结合律、乘法结合律和分配律等。

第二章整式的加减整式是由数或字母的积组成的式子，包括单项式和多项式。

单项式中的数字因数称为系数，所有字母的同类项次数一致。

多项式是几个单项式的和，其中每个单项式称为项，不含字母的项称为常数项。

多项式的次数是指次数最高项的次数，合并同类项是把所含字母相同并且相减的同类项的系数相加，作为合并后项的系数。

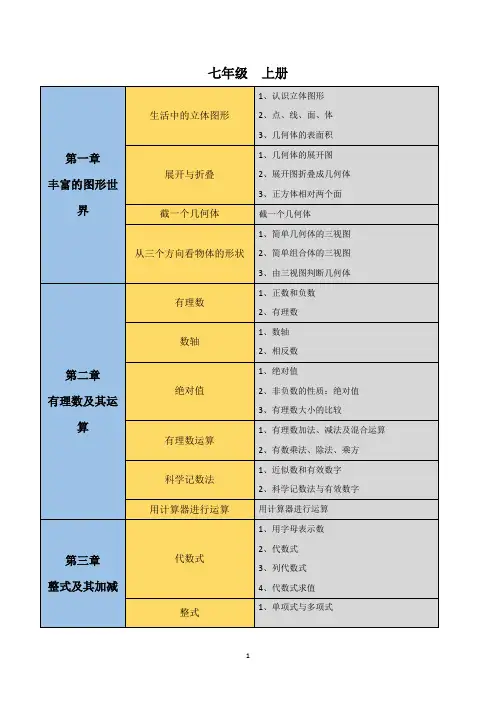
常见几何图形的基本概念思维导图常见几何图形：平面图形：三角形、矩形、正方形、梯形、菱形、圆形等立体图形：正方体、长方体、圆柱、圆锥、球体等几何图形的基本概念：三角形：三条边和三个角矩形：四条边和四个角，对边相等且平行正方形：四条边和四个角，对边相等且平行，角度为90度梯形：四条边和四个角，有两个平行边菱形：四条边和四个角，对边相等，角度为90度圆形：由一条曲线组成，每一点到圆心的距离相等正方体：六个面，每个面都是正方形长方体：六个面，相对的面都是相等的矩形圆柱：两个平行的圆面和一个侧面圆锥：一个圆锥面和一个底面球体：一个球面以上是常见几何图形的基本概念和特点，掌握它们对于几何研究和解题都非常重要。

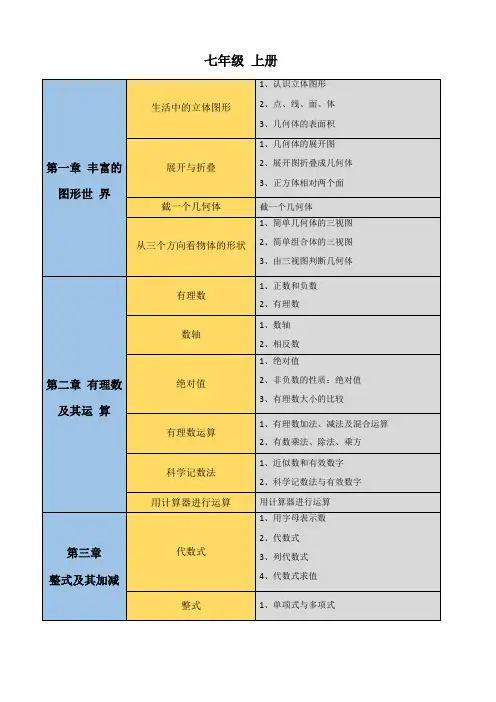
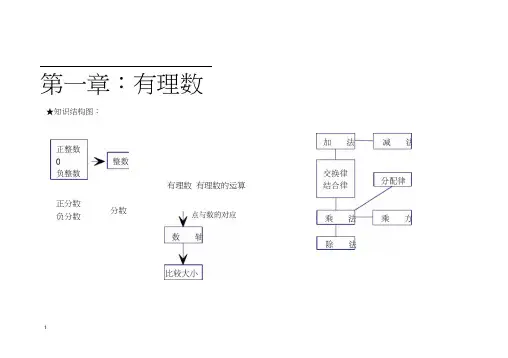
第一章：有理数★知识结构图：正分数负分数分数有理数有理数的运算第二章：整式的加减★知识结构图：2合并同类项整式的加减运式去括号★概念、定义：1. 都是数或字母的积的式子叫做单项式( monomial)，单独的一个数或一个字母也是单项式。

单项式中的数字因数叫做这个单项式的系数( coefficient )。

32. 一个单项式中，所有字母的指数的和叫做这个单项式的次数。

3. 几个单项的和叫做多项式，其中，每个单项式叫做多项式的项，不含字母的项叫做常数项4. 多项式里次数最高项的次数，叫做这个多项式的次数。

5. 把多项式中的同类项合并成一项，叫做合并同类项。

6. 合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母和字母的指数不变。

7. 如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；8. 如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反。

4第三章: 一元一次方程知识结构图：概念、定义：1. 含有一个未知数，未知数的次数都是1，这样的方程叫做一元一次方程。

3 等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等。

5. 等式的性质2：等式两边乘同一个数，或除以一个不为0 的数，结果仍相等。

56. 把等式一边的某项变号后移到另一边，叫做移项。

7. 工程问题：工作总量=工作效率×时间盈亏问题：利润=售价－成本利率=利润÷成本× 100％售价=标价×折扣数× 10％储蓄利润问题：利息=本金×利率×时间本息和=本金+利息图形的初步认识知识结构图：671. 我们把实物中抽象的各种图形统称为几何图形( geometric figure)2. 有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一平面内，它们是立体图形（figure ）。

3. 有些几何图形（如线段、角、三角形、长方形、圆等）的各部分都在同一平面内，它们是平面图形4. 点动成面，面动成线，线动成体。

⎩ ⎪ ⎪ ⎩ ⎪ ⎪第 1 章 有理数思维导图⎧ ⎧整数 ⎪按定义分⎨⎪ 分类⎨ ⎩分数 ⎧正有理数 ⎪按性质符号分⎪⎨0 ⎪⎩ ⎪负有理数 ⎧相反数— —只有符号不同的两个数，叫做互为相反数 ⎪ ⎪ ⎪绝对值— — ⎪ ⎪一般地，数轴上表示数a 的点与原点的距离， 叫做数a 的绝对值 ⎪倒数— —乘积是1的两个数互为倒数相关概念⎨ ⎪ ⎪乘方— — ⎪ ⎪ 求n 个相同因数的积的运算叫做乘方，乘方的结果叫做幂相同的因数叫做底数，相同因数的个数叫做指数 ⎪ ⎪科学记数法— —把一个数表示乘a ⨯10n 的形式（其中1 ≤ a < 10， ⎩⎪ n 是正整数），这种记数方法叫做科学记数法⎧⎪ ⎧有理数的加法法则 ⎪⎪有理数的减法法则 ⎪ ⎪法则⎨有理数的乘法法则 ⎪ ⎪ ⎪ 运算⎪ ⎪有理数的除法法则 ⎪ ⎪⎩乘方的运算符号法则 ⎨ ⎧ ⎧加法交换律 ⎪ ⎪交换律⎨ ⎪ ⎪ ⎩乘法交换律 ⎪ ⎪ ⎧加法结合律 ⎪运算律⎨结合律⎨ ⎪ ⎪ ⎩乘法结合律 ⎪ ⎪分配律 ⎪ ⎩⎪ ⎨ ⎪ ⎪ ⎪ ⎩ 第 2 章 整式的加减思维导图⎧用字母表示数 ⎪⎪ ⎧ ⎪ ⎪定义— —由数或字母的积组成的式子 ⎪ ⎪ ⎪单项式⎨系数— —单项式中的数字因数⎪ ⎪ ⎪ ⎪ ⎪ ⎩次数— —单项式中所有字母的指数的和 ⎪ ⎪ ⎧定义— —几个单项式的和 ⎪ ⎪ ⎪ ⎪项— —组成多项式的每个单项式 ⎪ 整⎪多项式⎨ ⎪ ⎪常数项— —不含字母的项式⎪⎪ ⎪ ⎪⎩次数 — —多项式中次数最高项的次数 加⎪ ⎧同类项 — —所含字母相同并且相同字母的指数也相同减⎪ ⎪ ⎪ ⎪ ⎪ ⎪合并同类项— — ⎪ ⎪ ⎪ ⎪ 把同类项的系数相加，所得的结果 作为合并后项的系数 ⎪ ⎪ ⎧括号外因数为正— — ⎪ ⎪ ⎪去括号后原括号内各项的符号与原来的符号相同 ⎪整式的加减⎨去括号⎪ ⎪ ⎨ ⎪ ⎪ ⎪括号外因数为负— — ⎪ ⎪ ⎪⎩去括号后原括号内各项的符号与原来的符号相反 ⎪ ⎪ ⎪ ⎪ ⎧⎪去括号 ⎪ ⎪步骤⎨⎩⎪ ⎪⎩合并同类项 的⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩第 3 章 一元一次方程思维导图⎧ ⎧方程：含有未知数的等式 ⎪ ⎪ ⎪ ⎪一元一次方程：只含有一个未知数(元)，未知数的次数都是1， ⎪ ⎪等号两边都是整式 ⎪一元一次方程⎨⎪ ⎪方程的解：使方程中等号左右两边相等的未知数的值 ⎪ ⎪ ⎪ ⎩解方程：求方程的解的过程 ⎪ ⎪ ⎧⎪性质1：等式两边加(或减)同一个数(或式子)，结果仍相等 ⎪等式的性质⎨⎪ ⎪⎩性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等 ⎪ ⎪ ⎧去分母 元⎪ ⎪ 一⎪ ⎪去括号 次⎨⎪⎪解一元一次方程的步骤⎨移项方⎪ ⎪ 程⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪列一元 ⎪ ⎪合并同类项 ⎪ ⎪系数化为1 ⎧审：弄清题意，分清已知量和未知量，明确各数量间的关系 ⎪ ⎪设：设未知数，并且用含未知数的代数式表示与所列方程有关的数量 ⎪ ⎪列：根据题目中的数量关系、相等关系、倍数关系以及若干倍多或少 ⎪一次方程⎨一个数字列方程 解应用题⎪ ⎪ ⎪ ⎪ ⎪解：解所列的方程，求出未知数的值以及题目中所要求的相关数量的值 ⎪ ⎪⎪ ⎪⎩验：检验所求的解是否符合题意，是否符合实际意义 一⎩ ⎨ ⎩ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎩⎩ 第 4 章 几何图形初步思维导图⎧ ⎧ ⎪ ⎪常见的立体图形 ⎪ ⎪ ⎪ ⎪ ⎧从正面看 ⎪立体图形 ⎪ ⎪ ⎨从不同的方向看立体图形⎨从左面看⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩立体图形的平面展示图 ⎪ ⎪从上面看 ⎪ ⎪ ⎪ ⎧表示方法 ⎪ 直线⎪特点 ⎪ ⎪基本事实：两点确定一条直线 ⎪ ⎪ ⎪ ⎪线⎨ ⎧表示方法⎪ ⎪ ⎪ 几何图形初步⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩ ⎪ 射线⎨ ⎩特点 ⎧表示方法 ⎪特点 ⎪比较方法 ⎪ ⎨基本事实：两点之间线段最短 ⎪平面图形⎨ ⎪两点之间的距离 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧定义 ⎪ ⎪ ⎪ ⎪ ⎪线段的中点 ⎪线段的和、差与画法 ⎪ ⎪ ⎪表示方法 ⎪ ⎪ ⎪ 比较大小的方法 ⎪ ⎪角⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎧互余 ⎪ ⎪ ⎪两角的特殊关系⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩角的度量 ⎩互补 线段 ⎧ ⎧“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

第一章 有理数思维导图 ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧<≤⨯⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧分配律乘法结合律加法结合律结合律乘法交换律加法交换律交换律运算律乘方的运算符号法则有理数的除法法则有理数的乘法法则有理数的减法法则有理数的加法法则法则运算方法叫做科学记数法是正整数），这种记数，的形式（其中把一个数表示乘——科学记数法数相同因数的个数叫做指相同的因数叫做底数，叫做幂叫做乘方，乘方的结果个相同因数的积的运算求——乘方的两个数互为倒数—乘积是—倒数的绝对值叫做数的点与原点的距离，一般地，数轴上表示数——绝对值数，叫做互为相反数—只有符号不同的两个—相反数相关概念负有理数正有理数按性质符号分分数整数按定义分分类有理数n 10a 110a n 1a a 0n第二章 整式的加减思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧合并同类项去括号步骤反的符号与原来的符号相去括号后原括号内各项——括号外因数为负同的符号与原来的符号相去括号后原括号内各项——括号外因数为正去括号作为合并后项的系数所得的结果把同类项的系数相加，——合并同类项同字母的指数也相同—所含字母相同并且相—同类项整式的加减的次数—多项式中次数最高项—次数—不含字母的项—常数项项式—组成多项式的每个单—项—几个单项式的和—定义多项式指数的和—单项式中所有字母的—次数—单项式中的数字因数—系数的式子—由数或字母的积组成—定义单项式用字母表示数减加的式整第三章 一元一次方程思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧际意义符合题意，是否符合实验：检验所求的解是否值中所要求的相关数量的出未知数的值以及题目解：解所列的方程，求一个数字列方程关系以及若干倍多或少关系、相等关系、倍数列：根据题目中的数量与所列方程有关的数量含未知数的代数式表示设：设未知数，并且用数量间的关系知量和未知量，明确各审：弄清题意，分清已解应用题一次方程列一元系数化为合并同类项移项去括号去分母解一元一次方程的步骤的数，结果仍相等，或除以同一个不为：等式两边乘同一个数性质，结果仍相等或式子同一个数或减：等式两边加性质等式的性质过程解方程：求方程的解的数的值号左右两边相等的未知方程的解：使方程中等等号两边都是整式，，未知数的次数都是元一个未知数一元一次方程：只含有式方程：含有未知数的等一元一次方程程方次一元一102)()(11)(第四章 几何图形初步思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧角的度量互补互余两角的特殊关系比较大小的方法表示方法定义角线段的和、差与画法线段的中点两点之间的距离段最短基本事实：两点之间线比较方法特点表示方法线段特点表示方法射线条直线基本事实：两点确定一特点表示方法直线线平面图形立体图形的平面展示图从上面看从左面看从正面看形从不同的方向看立体图常见的立体图形立体图形几何图形初步。

第一章有理数思维导图分配律乘法结合律加法结合律结合律乘法交换律加法交换律交换律运算律乘方的运算符号法则有理数的除法法则有理数的乘法法则有理数的减法法则有理数的加法法则法则运算方法叫做科学记数法是正整数），这种记数，的形式（其中把一个数表示乘——科学记数法数相同因数的个数叫做指相同的因数叫做底数，叫做幂叫做乘方，乘方的结果个相同因数的积的运算求——乘方的两个数互为倒数—乘积是—倒数的绝对值叫做数的点与原点的距离，一般地，数轴上表示数——绝对值数，叫做互为相反数—只有符号不同的两个—相反数相关概念负有理数正有理数按性质符号分分数整数按定义分分类有理数n 10a 110a n 1a a 0n第二章整式的加减思维导图合并同类项去括号步骤反的符号与原来的符号相去括号后原括号内各项——括号外因数为负同的符号与原来的符号相去括号后原括号内各项——括号外因数为正去括号作为合并后项的系数所得的结果把同类项的系数相加，——合并同类项同字母的指数也相同—所含字母相同并且相—同类项整式的加减的次数—多项式中次数最高项—次数—不含字母的项—常数项项式—组成多项式的每个单—项—几个单项式的和—定义多项式指数的和—单项式中所有字母的—次数—单项式中的数字因数—系数的式子—由数或字母的积组成—定义单项式用字母表示数减加的式整第三章一元一次方程思维导图际意义符合题意，是否符合实验：检验所求的解是否值中所要求的相关数量的出未知数的值以及题目解：解所列的方程，求一个数字列方程关系以及若干倍多或少关系、相等关系、倍数列：根据题目中的数量与所列方程有关的数量含未知数的代数式表示设：设未知数，并且用数量间的关系知量和未知量，明确各审：弄清题意，分清已解应用题一次方程列一元系数化为合并同类项移项去括号去分母解一元一次方程的步骤的数，结果仍相等，或除以同一个不为：等式两边乘同一个数性质，结果仍相等或式子同一个数或减：等式两边加性质等式的性质过程解方程：求方程的解的数的值号左右两边相等的未知方程的解：使方程中等等号两边都是整式，，未知数的次数都是元一个未知数一元一次方程：只含有式方程：含有未知数的等一元一次方程程方次一元一102)()(11)(第四章几何图形初步思维导图角的度量互补互余两角的特殊关系比较大小的方法表示方法定义角线段的和、差与画法线段的中点两点之间的距离段最短基本事实：两点之间线比较方法特点表示方法线段特点表示方法射线条直线基本事实：两点确定一特点表示方法直线线平面图形立体图形的平面展示图从上面看从左面看从正面看形从不同的方向看立体图常见的立体图形立体图形几何图形初步。

七年级数学上册《有理数》思维导图分析知识点与考点梳理1.大于0的数叫做正数。

2.在正数前面加上负号“-”的数叫做负数。

3.整数和分数统称为有理数。

4.人们通常用一条直线上的点表示数，这条直线叫做数轴。

5.在直线上任取一个点表示数0，这个点叫做原点。

6.一般的，数轴上表示数a的点与原点的距离叫做数a的绝对值。

7. 由绝对值的定义可知：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0。

8.正数大于0，0大于负数，正数大于负数。

9.两个负数，绝对值大的反而小。

10.有理数加法法则：(1)同号两数相加，取相同的符号，并把绝对值相加。

(2)绝对值不相等的异号两数相加，取绝对值较大的加数的负号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0。

(3)一个数同0相加，仍得这个数。

11.有理数的加法中，两个数相加，交换交换加数的位置，和不变。

12.有理数的加法中，三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

13.有理数减法法则：减去一个数，等于加上这个数的相反数。

14.有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值向乘。

任何数同0相乘，都得0。

15.有理数中仍然有：乘积是1的两个数互为倒数。

16.一般的，有理数乘法中，两个数相乘，交换因数的位置，积相等。

17. 三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等。

18. 一般地，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。

19.有理数除法法则：除以一个不等于0的数，等于乘这个数的倒数。

20.两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不等于0的数，都得0。

21. 求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

在an 中，a叫做底数，n叫做指数。

22.根据有理数的乘法法则可以得出：负数的奇次幂是负数，负数的偶次幂是正数。

显然，正数的任何次幂都是正数，0的任何次幂都是0。

第一章 丰富的图形世界⎧⎧⎧⎪⎨⎪⎪⎩⎪⎨⎪⎧⎨⎪⎨⎪⎪⎩⎩⎪⎪⎩⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩棱柱：n 棱柱有__个顶点，__条棱，__个面柱体圆柱几何体生活中的立体图形棱锥：n 棱锥有__个顶点，__条棱，__个面锥体圆锥：构成：点动成__,线动成__,面动成__平面展开图正方体展开与折叠丰对立面富的图形正方体______________________________世界圆柱___________________截一个几何体⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩____________圆锥_________________________________圆_________________________________主视图左视图从三个方向看俯视图第二章 有理数 ________________________________________________________________________________________⎧⎧⎨⎪⎩⎪⎪⎧⎨⎪⎪⎨⎪⎪⎪⎩⎩按定义分分类按性质符号分数轴：三要素：几何意义：代数意义：____________________，叫做互为相反数。

相反数——字母表示：a 的相反数是____,a+b 的相反数是__理数相关概念________01a ⎧⎪⎪⎨⎪⎪⎩⎧⎪≥⎧⎪⎨⎨≤⎩⎪⎪⎩__性质：若a,b 互为相反数，则_____________.几何意义：___________________________，a 0绝对值——代数意义：a=____，a 0性质：非负性倒数——乘积是的两个数互为倒数. 正数的倒数是___,负数的倒数是___，0的倒数是_____._____________________乘方——1a 10n ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪≤<⎪⎪⎩⎧⎪⎪⎪⎨⎪⎪⎪⎩叫做乘方，乘方的结果叫做____相同的因数叫做_____，_________________叫做指数把一个数表示成_______的形式（其中，科学记数法——是正整数），这种记数方法叫做科学记数法有理数的加法法则有理数的减法法则运算法则有理数的乘法法则有理数的除法法则乘方的运算符号法则⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩第三章 整式的加减⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩用字母表示数定义——由_______________组成的式子单项式系数——单项式中的_____________次数——单项式中____________的和定义——几个单项式的和项——组成多项式的每个单项式多项式常数项——不含字母的项整式次数——多项中________________________的加减同类项——____________相同并整式的加减⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎧⎪⎪⎨⎪⎪⎪⎩⎩⎩且____________________也相同把同类项的系数相加，所得的结果合并同类项——作为合并后项的系数括号外因数为正:去括号后原括号内各项的符号与原来的符号____去括号括号外因数为负:去括号后原括号内各项的符号与原来的符号______去括号步骤合并同类项⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪第四章 基本平面图形1._________2.____________________1._________________2._________________D AB ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧⎨⎪⎩⎪⎪⎪⎪⎧⎨⎪⎩⎪⎪⎩ 图形 表示方法 延伸方向 端点个数 能否度量线段射线线直线比较线段的长短：方法线段的中点：若点是线段的中点，则公理尺规作图：作一条线段等于已知线段平面图形角 1.___________2.___________________________1.2.OC AOB ⎧⎨⎩∠具有的两条组成的图形定义一条绕旋转得到的图形表示方法：比较大小的方法：1.______2._______角平分线：若射线是的角平分线，则角度换算:___________________角的计算钟面角:时针1小时转____,1分钟转______ 分针1小时转_____,1分钟转⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎪⎪⎨⎪⎪⎪⎩⎩⎧⎧⎨⎪⎩⎪⎪⎧⎪⎨⎪⎧⎪⎪⎨⎪⎪⎨⎪⎪⎪⎪⎪⎩⎩⎩_____定义：_________________________多边形对角线:一个顶点出发有___条，共有__条圆心，半径，弧多边形与圆圆心角____________________圆扇形周长:公式：______________面积:公式：________________⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩第五章 一元一次方程1.________2.3.________1()()⎧⎪⎪⎪⎧⎪⎪⎪⎨⎪⎪⎨⎩⎪⎪⎪⎪⎪⎪⎩方程：____________________只含有一元一次方程未知数的指数是______一元一次方程等式两边都是方程的解：使方程中等号左右两边相等的______的值解方程：求方程的解的过程性质：等式两边加或减同一个数或式子，结果仍相等 字母表示：如果a=b,则______等式的性质一元一次方程201.____________2.____________3.____________4.____________5._____________⎧⎪⎪⎪⎨⎪⎪⎪⎩⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩__________性质：等式两边乘同一个数，或除以同一个不为的数，结果仍相等 字母表示：如果a=b,则__________________解一元一次方程的步骤审：弄清题意列一元一次方程解应用题⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩⎩，分清已知量和未知量，明确各数量间的关系设：设未知数，并且用含未知数的代数式表示与所列方程有关的数量列：根据题目中的数量关系、相等关系、倍数关系以及若干倍多或少一个数字列方程解：解所列的方程，求出未知数的值以及题目中所要求的相关数量的值验：检验所求的解是否符合题意，是否符合实际意义⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪2:________________________1:_______________________2:_______________________3:_______________________1.⎧⎪⎨⎪⎩⎧⎪⎪⎪⎨⎪⎪⎪⎩等量关系1：_______________________水箱变高了等量关系希望工程:公式打折销售公式公式直线型：线段图表示____相遇问题一元一次方行程问题程应用题______________________________________________2.3.⎧⎪⎨⎪⎩⎧⎧⎪⎪⎪⎪⎨⎪⎨⎪⎪⎪⎩⎪⎪⎩_________________环形跑道：公式同地不同时：直线型：线段图表示追击问题同时不同地：_____________________环形跑道：公式___________________________航行问题:等量关系为_______________1.________________________a ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎩_十位数为a,个位数为b,则这个两位数表示为_________数字问题 2.百位数为a,十位数为b,个位数为c,则这个三位数表示为________日历问题：第六章 数据的收集与整理⎧⎪⎨⎪⎩⎧⎨定义：__________________________普查总体：___________________________个体：____________________________数据的收集方式定义:________________________抽样调查样本:_________________________样本容量:______________________数据的收集与整理 1.2.______________________________________1.2.⎧⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩⎩⎧⎪⎨⎪⎩优点：__________________________扇形统计图:步骤：_____________________________优点______________________________极值________条形统计图数据的整理频数直方图⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎧⎪⎪⎪⎨⎪⎪⎪⎨⎨⎪⎪⎪⎪⎪⎪⎩⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎩___________组距___________________频数____________________折线统计图:优点：_____________________________。